- 1.34 MB
- 2022-04-29 14:00:48 发布
- 1、本文档共5页,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,可选择认领,认领后既往收益都归您。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细先通过免费阅读内容等途径辨别内容交易风险。如存在严重挂羊头卖狗肉之情形,可联系本站下载客服投诉处理。
- 文档侵权举报电话:19940600175。
'第三章思考题1.试说明集总参数法的物理概念及数学处理的特点答:当内外热阻之比趋于零时,影响换热的主要环节是在边界上的换热能力。而内部由于热阻很小而温度趋于均匀,以至于不需要关心温度在空间的分布,温度只是时间的函数,数学描述上由偏微分方程转化为常微分方程、大大降低了求解难度。2.在用热电偶测定气流的非稳态温度场时,怎么才能改善热电偶的温度响应特性?cvc答:要改善热电偶的温度响应特性,即最大限度降低热电偶的时间常数hA,形状上要降低体面比,要选择热容小的材料,要强化热电偶表面的对流换热。3.试说明”无限大平板”物理概念,并举出一二个可以按无限大平板处理的非稳态导热问题答;所谓“无限大”平板,是指其长宽尺度远大于其厚度,从边缘交换的热量可以忽略不计,当平板两侧换热均匀时,热量只垂直于板面方向流动。如薄板两侧均匀加热或冷却、炉墙或冷库的保温层导热等情况可以按无限大平板处理。4.什么叫非稳态导热的正规状态或充分发展阶段?这一阶段在物理过程及数学处理上都有些什么特点?答:非稳态导热过程进行到一定程度,初始温度分布的影响就会消失,虽然各点温度仍随时间变化,但过余温度的比值已与时间无关,只是几何位置(x/)和边界条件(Bi数)的函数,亦即无量纲温度分布不变,这一阶段称为正规状况阶段或充分发展阶段。这一阶段的数学处理十分便利,温度分布计算只需取无穷级数的首项进行计算。5.有人认为,当非稳态导热过程经历时间很长时,采用图3-7记算所得的结果是错误的.理由是:这个图表明,物体中各点的过余温度的比值与几何位置及Bi有关,而与时间无关.但当时间趋于无限大时,物体中各点的温度应趋近流体温度,所以两者是有矛盾的。你是否同意这种看法,说明你的理由。答:我不同意这种看法,因为随着时间的推移,虽然物体中各点过余温度的比值不变但各点温度的绝对值在无限接近。这与物体中各点温度趋近流体温度的事实并不矛盾。6.试说明Bi数的物理意义。Bio及Bi各代表什么样的换热条件?有人认为,Bi代表了绝热工况,你是否赞同这一观点,为什么?答;Bi数是物体内外热阻之比的相对值。Bio时说明传热热阻主要在边界,内部温度趋于均匀,可以用集总参数法进行分析求解;Bi时,说明传热热阻主要在内部,可以近似认为壁温就是流体温度。认为Bio代表绝热工况是不正确的,该工况是指边界热阻相对于内部热阻较大,而绝热工况下边界热阻无限大。7.什么是分非稳态导热问题的乘积解法,他的使用条件是什么?
答;对于二维或三维非稳态导热问题的解等于对应几个一维问题解的乘积,其解的形式是无量纲过余温度,这就是非稳态导热问题的乘积解法,其使用条件是恒温介质,第三类边界条件或边界温度为定值、初始温度为常数的情况。8.什么是”半无限大”的物体?半无限大物体的非稳态导热存在正规阶段吗?答:所谓“半大限大”物体是指平面一侧空间无限延伸的物体:因为物体向纵深无限延伸,初脸温度的影响永远不会消除,所以半死限大物体的非稳念导热不存在正规状况阶段。9.冬天,72℃的铁与600℃的木材摸上去的感觉一样吗,为什么?10.本章的讨论都是对物性为常数的情形作出的,对物性温度函数的情形,你认为怎样获得其非稳态导热的温度场?2答:从分析解形式可见,物体的无量纲过余温度是傅立叶数(/l)的负指数函数,即表示在相同尺寸及换热条件下,导温系数越大的物体到达指定温度所需的时间越短、这正说明导温系数所代表的物理含义。习题基本概念及定性分析3-1设有五块厚30mm的无限大平板,各用银、铜、钢、玻璃及软木做成,初始温度均匀000(20C),两个侧面突然上升到60C,试计算使用中心温度上升到56C时各板所需的时间。-62-62-62-62五种材料的热扩散依次为170×10m/s、103×10m/s,12.9×10m/s、0.59×10m/s-62及0.155×10m/s。由此计算你可以得出什么结论?解:一维非稳态无限大平板内的温度分布如下函数关系式:ttx0f(Bi,Fo,)tt00不同材料的无限大平板,均处于第一类边界条件(即Bi)。由题意知材料达到同样工况式Bi数和x/相同,要使温度分布相同,则只需Fo数相同()()(Fo)(Fo)2122因此,12,即,而相等故知小所需时间大铜银钢玻璃软木所以铜银钢玻璃软木。3-2设一根长为l的棒有均匀初温度t0,此后使其两端在恒定的t1(x=0)及t2>t1>t0。棒的四周保持绝热。试画出棒中温度分布随时间变法的示意曲线及最终的温度分布曲线。解:由于棒的四周保持绝热,因而此棒中的温度分布相当于厚为l的无限大平板中的分布,随时间而变化的情形定性的示于图中.
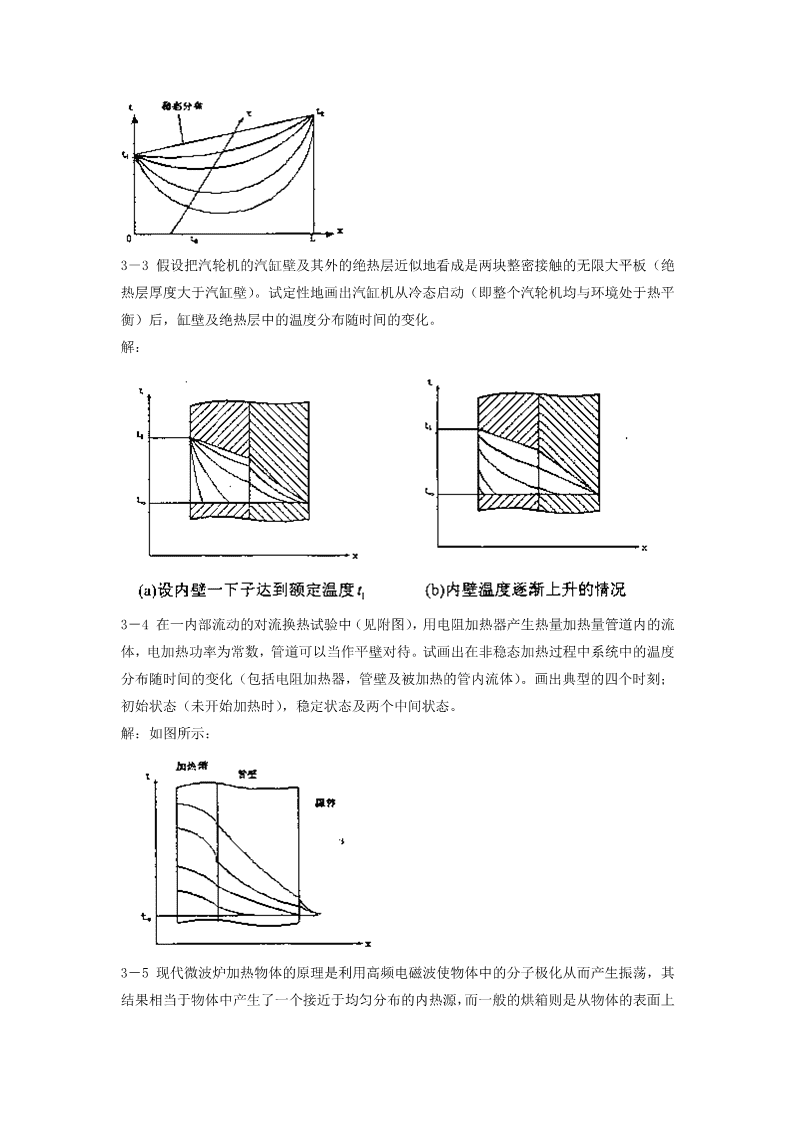
3-3假设把汽轮机的汽缸壁及其外的绝热层近似地看成是两块整密接触的无限大平板(绝热层厚度大于汽缸壁)。试定性地画出汽缸机从冷态启动(即整个汽轮机均与环境处于热平衡)后,缸壁及绝热层中的温度分布随时间的变化。解:3-4在一内部流动的对流换热试验中(见附图),用电阻加热器产生热量加热量管道内的流体,电加热功率为常数,管道可以当作平壁对待。试画出在非稳态加热过程中系统中的温度分布随时间的变化(包括电阻加热器,管壁及被加热的管内流体)。画出典型的四个时刻;初始状态(未开始加热时),稳定状态及两个中间状态。解:如图所示:3-5现代微波炉加热物体的原理是利用高频电磁波使物体中的分子极化从而产生振荡,其结果相当于物体中产生了一个接近于均匀分布的内热源,而一般的烘箱则是从物体的表面上
进行接近恒热流的加热。设把一块牛肉当作厚为2的无限大平板,试定性地画出采用微0波炉及烘箱对牛肉加热(从室温到最低温度为85C)过程中牛肉的温度分布曲线(加热开始前,加热过程中某一时刻及加热终了三个时刻)。解:假设:辐射加热时表面热源均匀;散热略而不计.集总参数法分析3-6一初始温度为t0的物体,被置于室温为t的房间中。物体表面的发射率为,表面与空气间的换热系数为h。物体的体集积为V,参数与换热的面积为A,比热容和密度分别为c及。物体的内热阻可忽略不计,试列出物体温度随时间变化的微分方程式。解:由题意知,固体温度始终均匀一致,所以可按集总热容系统处理固体通过热辐射散到周围的热量为:44qA(TT)1固体通过对流散到周围的热量为:qhA(TT)2固体散出的总热量等于其焓的减小dtqqcv12d即44dtA(TT)hA(TT)cvd3-7如图所示,一容器中装有质量为m、比热容为c的流体,初始温度为tO。另一流体在管内凝结放热,凝结温度为t。容器外壳绝热良好。容器中的流体因有搅拌器的作用而可认为任一时刻整个流体的温度都是均匀的。管内流体与容器中流体间的总传热系数k及传热面积A均为以知,k为常数。试导出开始加热后任一时刻t时容器中流体温度的计算式。解:按集总参数处理,容器中流体温度由下面的微分方程式描述dthA(TT)cv1d
ttkA1exp()ttc此方程的解为013-8一具有内部加热装置的物体与空气处于热平衡。在某一瞬间,加热装置投入工作,其.Q作用相当于强度为的内热源。设物体与周围环境的表面传热系数为h(常数),内热阻可以忽略,其他几何、物性参数均以知,试列出其温度随时间变化的微分方程式并求解之。解:集总参数法的导热微分方程可以利用能量守恒的方法得到dtcvhA(tt)d引入过余温度,则其数学描写如下:dcvhAd(0)tt0hAhAcvcvtte(1e)0故其温度分布为:hA2cv/AKJ/(mK)003-9一热电偶的之值为2.094,初始温度为20C,后将其置于320C2W/(mk)的气流中。试计算在气流与热电偶之间的表面传热系数为58的两种情况下,热电偶的时间常数并画出两种情况下热电偶读数的过余温度随时间变化的曲线。cvc解:由hA2h58W/(mK)c0.036s当时,2h116W/(mK)c0.018s当时,003-10一热电偶热接点可近似地看成为球形,初始温度为25C,后被置于温度为200C地气1s流中。问欲使热电偶的时间常数c热接点的直径应为多大?以知热接点与气流间的表235W/(mK)20W/(mk)面传热系数为,热接点的物性为:,3c400J/(kgk),8500kg/m,如果气流与热接点之间还有辐射换热,对所需的热接点直径有何影响?热电偶引线的影响忽略不计。cvc解:由于热电偶的直径很小,一般满足集总参数法,时间常数为:hAtch13505V/AR/310.2910mc8500400故
5热电偶的直径:d2R2310.29100.617m验证Bi数是否满足集总参数法5h(V/A)35010.2910Bi0.00180.0333v20故满足集总参数法条件。若热接点与气流间存在辐射换热,则总表面传热系数h(包括对流和辐射)增加,由cvchA知,保持c不变,可使V/A增加,即热接点直径增加。3-11一根裸露的长导线处于温度为t的空气中,试导出当导线通以恒定电流I后导线温度变化的微分方程式。设导线同一截面上的温度是均匀的,导线的周长为P,截面积为Ac比e热容为c,密度为电阻率为,与环境的表面传热系数为h,长度方向的温度变化略而23.45g/m,c460J/(kgK)3.6310/m不计。若以知导线的质量为,电阻值为,电流为8A,试确定导线刚通电瞬间的温升率。dt2rdx解:对导线的任意段长度dx作热平衡,可得:AdxchPdx(tt)I(),cdA2dIrhP令tt,可得:,0,tt0,2dAcAc在通电的初始瞬间,tt0,则有:2dIr2r111211l883.63101.46K/s.23dAcAcAcc3.45104603-12一块单侧表面积为A、初温为t0的平板,一侧表面突然受到恒定热流密度q0的加热,t另一侧表面受到初温为的气流冷却,表面传热系数为h。试列出物体温度随时间变化的微分方程式并求解之。设内阻可以不计,其他的几何、物性参数均以知。解:由题意,物体内部热阻可以忽略,温度只是时间的函数,一侧的对流换热和另一侧恒热流加热作为内热源处理,根据热平衡方程可得控制方程为:dtcvhA(tt)Aqw0dt/tt00tt引入过余温度则:dcvhAAq0wd/t00
hAqcvwBe上述控制方程的解为:hqwB0由初始条件有:h,故温度分布为:hAqhAwttexp()(1exp())0cvhcv003-13一块厚20mm的钢板,加热到500C后置于20C的空气中冷却。设冷却过程中钢板两2235W/(mK)45W/(mK)侧面的平均表面传热系数为,钢板的导热系数为,若扩散率为521.37510m/s。试确定使钢板冷却到空气相差100C时所需的时间。hABi0.00780.1解:由题意知故可采用集总参数法处理。由平板两边对称受热,板内温度分布必以其中心对称,建立微分方程,引入过余温度,则得:dcvhA0d(0)tt0hAhhexp()exp()exp()cvc(V/A)解之得:00当10C时,将数据代入得,=3633s003-14一含碳约0.5%的曲轴,加热到600C后置于20C的空气回火。曲轴的质量为7.84kg,32418.7J/(kgK)7840kg/m0表面积为870cm,比容为,密度为可按300C查取,冷却过程229.1W/(mK)0的平均表面传热系数取为。问经多长时间后,曲轴可冷却到于空气相差10C。解:Bi0.0570.05故不采用集总参数法,改用诺漠图10m0.017600200,查附录2图1得Fo=22Fo2,5267s22RcR3-15一种火焰报警器采用低熔点的金属丝作为传热元件,当该导线受火焰或高温烟气的作0210W/(mK)用而熔断时报警系统即被触发,一报警系统的熔点为500C,,37200kg/mc420J/(kgK)00,,初始温度为25C。问当它突然受到650C烟气加热后,为在1min内发生报警讯号,导线的直径应限在多少以下?设复合换热器的表面换热系
212W/(mK)数为。解:采用集总参数法得:hAexp()cv5000C0,要使元件报警则500650hAexp()25650cv,代入数据得D=0.669mm验证Bi数:h(V/A)hD3Bi0.0095100.054,故可采用集总参数法。3-16在热处理工艺中,用银球试样来测定淬火介质在不同条件下的冷却能力。今有两个直径为20mm的银球,加热到6000C后被分别置于200C的盛有静止水的大容器及200C的循环水中。用热电偶测得,当因球中心温度从6500C变化到4500C时,其降温速率分别为1800C/s及3600C/s。试确定两种情况下银球表面与水之间的表面传热系数。已知在上述温度范围内23c2.6210J/(kgk)、10500kg/m、=360W/(mK)银的物性参数为。解:本题表面传热系数未知,即Bi数为未知参数,所以无法判断是否满足集总参数法条件。为此,先假定满足集总参数条件,然后验算hAexp()cv(1)对静止水情行,由0,代入数据6502030,430,V/AR/30.00333,200/1801.1150c(V/A)02hln()3149W/(mK)验算Bi数h(V/A)h(R/3)Bi0.02910.0333v,满足集总参数条件。(2)对循环水情形,同理,200/3600.56sc(V/A)02hln()6299W/(mK)按集总参数法时h(V/A)h(R/3)Bi0.05830.0333v验算Bi数,不满足集总参数条件改用漠渃图2Fo0.72722RcR此时
430m0.6836300,查图得124.5,故hBi8000W/mkBiR3-17等离子喷镀是一种用以改善材料表面特性(耐腐蚀、耐磨等)的高新技术。陶瓷是常4用的一种喷镀材料。喷镀过程大致如下:把陶瓷粉末注入温度高达10K的等离子气流中,在到达被喷镀的表面之前,陶瓷粉末吸收等离子气流的热量迅速升温到熔点并完全溶化为液AlO滴,然后被冲击到被喷镀表面迅速凝固,形成一镀层。设三氧化二铝(23)粉末的直径D50m3970kg/m311W/(mk)为p,密度,导热系数,比热容2c1560J/(kgK)10000W/(mK),这些粉末颗粒与气流间的表面换热系数为,粉末3580kJ/kg颗粒的熔点为2350K,熔解潜热为。试在不考虑颗粒的辐射热损失时确定从t0=3000K加热到其熔点所需的时间,以及从刚达到熔点直至全部熔为液滴所需时间。6hR10002510Bi0.0680.1v解:11,可按集总参数法计算:100003009700K,1000023507650K0,hA3h310000exp()exp()exp()60cVcR397015602510,7650exp(193.76)0.788739700,193.760.2374,1.2210s,34R2Rr:r4Rhtht计算所需熔化时间:3,3,63Rr2510397035801035531531.5510s83ht310000(100002350)2.29510。3-18直径为1mm的金属丝置于温度为250C的恒温槽中,其电阻值为0.01/m。设电阻强度为120A的电流突然经过此导线并保持不变,导线表面与油之间的表面传热系数为2550W/(mK),问当导线温度稳定后其值为多少?从通电开始瞬间到导线温度与稳定时0之值相差1C所需的时间为多少?设表面传热系数保持为常数,导线的3c500J/(kgk)、8000kg/m、=25W/(mK)。一维非稳态导热
2hD(tt)IR解:(1)稳定过程热平衡:w2IR0tt108.4CwDhtt(3)可采用集总参数法:令,由热平衡dvcVhA0d0,0dhAcVhA0Cexp()dcV解齐次方程vhACexp()1hAcV0,o方程的解为:,由得vC,代入数据得=8.04s1hA(a)无限大平板一维非稳态3-19作为一种估算,可以对汽轮机启动过程中汽缸壁的升温过程作近似分析:把汽缸壁看成是一维的平壁,启动前汽缸壁温度均匀并为t0,进入汽轮机的蒸汽温度与时间成线性关系,tt及ff0,其中为蒸汽温速率,汽缸壁与蒸汽间的表面传热系数h为常数,汽缸壁外表面绝热良好。试对这一简化模型列出汽缸壁中温度的数学描写式。2tta2解:x(0x)t(x,o)t0x0()tht(tw)f0xx,t0xx0,3-20在一个无限大平板的非稳态导热过程中,测得某一瞬间在板的厚度方上的三点A、B、000t180C、t130C、t900CC处的温度分别为ABC,A与B及B与C各相隔1cm,材52料的热扩散率1.110m/s。试估计在该瞬间B点温度对时间的瞬间变化率。该平板
的厚度远大于A、C之间的距离。2ttta(tA2tBtC)a22解:x的离散形式为:xt51802130901.1101.1K/s2代入已知数据可得B点的瞬时变化率为:0.013-21有两块同样材料的平板A及B,A的厚度为B的两倍,从统一高温炉中取出置于冷流体中淬火。流体与各表面间的表面传热系数均可视为无限大。已知板B中心点的过余温度下降到初值的一半需要20min,问A板达到同样温度工况需要的时间?m解:BiBif(Fo)AB0mm0.5FoFoAB0A0Baa,2ABABA2()4420min80minABBB23-22某一瞬间,一无内热源的无限大平板中的温度分布可以表示成t1=c1x+c2的形式,其中c1、c2为已知的常数,试确定:(1)此时刻在x=0的表面处的热流密度(2)此时刻平板平均温度随时间的变化率,物性已知且为常数。dt解:2Cx1dxdt(1)q0x0x0dxdt(2)q2Cxx1dx由能量平衡:dtcAqAxddt2CA1则2C1dcA03-23一截面尺寸为10cm×5cm的长钢棒(18-20Gr/8-12Ni),初温度为20C,然后长边
20h125W/(mK)的一侧突然被置于200C的气流中,,而另外三个侧面绝热。试确定6min、c、v0后长边的另一侧面中点的温度。钢棒可以近似地取用为20C时之值。3解:查表钢棒的物性参数为:7820kg/m,c460J/kgK,15.2W/mK按题意可作半壁厚为0.05m的对称半无限大平板处理6=4.225510Fo0.608472ch1250.05Bi0.411815.2解超越方程=0.615841m2sin12由式(3-22)计算:exp(Fo)0.843521sincos01110t0.84352(tt)t48.17Cm0ff3-24一高H=0.4m的圆柱体,初始温度均匀,然后将其四周曲面完全绝热,而上、下底面250W/(mK)暴露于气流中,气流与两端面间的表面传热系数均为。圆柱体导热系数20W/(mk)5.6106m2/s,热扩散率。试确定圆柱体中心过余温度下降到初值一半时间所需的时间。解:因四周表面绝热,这相当于一个厚为20.4m的无限大平壁的非稳态导热问题,mh500.20.5,B0.5i200220.2F1.7,F1.712142s3.37h006a5.610由图3-6查得003-25有一航天器,重返大气层试壳体表面温度为1000C,随即落入温度为5C的海洋中,21135W/(mK)设海水与壳体表面间的传热系数为,试问此航天器落入海洋后5min时表面温度是多少?壳体壁面中最高温度是多少?壳体厚50mm,56.8W/(mk),624.1310m/s,其内侧可认为是绝热的。6156.8a4.13103001.0,F0.496022解:Bih11350.050.05mlml0.80.65,0.80.650.520m0m由图3-6查得,由图3-7查得00tt0.8(tt)50.8(10005)801C,t50.52995522Cmnnm
03-26厚8mm的瓷砖被堆放在室外货场上,并与-15C的环境处于热平衡。此后把它们搬入025C的室内。为了加速升温过程,每快瓷砖被分散地搁在墙旁,设此时瓷砖两面与室内环境24.4W/(mK)0地表面传热系数为。为防止瓷砖脆裂,需待其温度上升到10C以上才可操作,72问需多少时间?已知瓷砖地7.510m/s,1.1W/(mk)。如瓷砖厚度增加一倍,其它条件不变,问等待时间又为多长?00m11.1102515C,152540C,0.375,62.5.m0Bi4.40.004解:0由图3-6查得220.004F60.F601280s21.3min007a7.510厚度加倍后,2210.00831.25,查得F31,F312645s44min007Bia7.5103-27汽轮机在启动一段时间后,如果蒸汽速度保持匀速上升,则汽缸壁中的温度变化会达到或接近这样的工况:壁中各点的温度对时间的偏导数即不随时间而异,又不随地点而变(称准稳态工况)。试对准工况导出汽缸壁中最大温差的计算公式。解:把气缸壁作为平壁处理且假定其外表面绝热,如右图所示,则准稳态工况时气缸壁中温度分布可用下列数学式描写:2dtwdt,x0,0,x,tt2w2dadx式中w为气缸壁的升温速度,K/s。221wx1wtcxc,由边界条件得,c0,ct,112w22a2a上式的通解为221w(x)tt,最大温差是x0及x处的壁温差其值为w22a故得221w1wtt(t),w2w22a2a03-28一块后300mm的板块钢坯(含碳近似为0.5%)的初温为20C,送于温度为12000C
的炉子里单侧加热,不受热侧面可近似地认为是绝热的。已知钢板热扩散率62Wm2K5.5510m/s,加热过程中平均表面传热系数为290/(),设确定加热到钢00板表面温度低于炉温15C时所需的时间,及此时钢板两表面间的温差。导热系数可按600C查附录。sincos111ln2sincos011由式(3-21)Fo2.78545212Fo45169s12.55h15由式(3-23):36.4mcoscos1.14611015(36.4)21.4Cm329、已知:初温为t厚为2的无限大平板,两表面的温度突然降到t0,,此后平板中各点的温度按下式计算:41n/22anxesin0n1n2其中tx,t,ttw00w62今有一厚为3cm的平板,t150C,t30C,a210m/s0w求:用上式(仅取无穷级数的的第一项)计算1min后平板中间截面上的温度,并与海斯勒图及(3-27)相比较,又,如取级数的前四项来计算,对结果有何影响?解:由所给出的解的形式可以看出,此时坐标原点是取在板的一侧表面上的(x=0,x226tt0),对于板的中心,,()a()(210)601.31595,12220.034m41.31995a21060m故得e0.3415,由0.5333,由图3-6查得0.34.220.01500如取前四项,得:m41.31995115.8435164.481(e-ee)370481529(0.26824.3866101.0310101.415510)0.3415在四位有效数字内与取级数一项的结果毫无差别。按分析解t301200.341570.98C.wT1500K3-30火箭发动机的喷管在起动过程中受到的高温燃气加热,受材料的限制0其局部壁温不得大于150K.为延长运行时间在喷管内壁喷涂了一层厚10mm的陶瓷,其物10W/(mk)6106m2/s性参数为,。试对此情况下喷管能承受的运行时间作一
2h2500W/(mK)保守的估计。设内表面与高温燃气间的表面传热系数为,喷管的初始T300K温度o。解:一种保守的估计方法是假定喷管壁面是绝热的,则相当于厚为2δ1的平板,15002300800h25000.01m2,0.4,Bi2.5,x/0,30023002000100m2F2FAe10f()Ae10,102b10.918811(a)(0.4022)(0.40220.3675)1.2992,1Bi2.5cBi0.42712.51.1398,Aab(1e)1.01010.2575(1e)11.067751.01010.2575(1e)1.01010.2575(10.3438)1.10595,20.41.10595e12992F0,ln0.4ln1.105951.29922F,01.0170.91630.10071.6879F,F0.6025,001.687965a61020.60256.03106.030.6025,0.011010.05s22660.016106106imi分析:如果喷管表面不涂层,则允许使用的条件是0.4,00mim由于1,因而此时必大于0.4,在相同的Bi下,F必小于0.603,如果相同,0m0则由于陶瓷的a小于金属的a,因而所允许的值必更小。03-31一火箭发动机喷管,壁厚为9mm,出世温度为30C。在进行静推力试验时,温度为1201950W/(mK)750C的高温燃气送于该喷管,燃气与壁面间的表面传热系数为。喷管材38400kg/m24.6W/(mk)c560J/(kgK)料的密度,导热系数为,。假设喷管因直径与厚度之比较大而可视为平壁,且外侧可作绝热处理,试确定:(1)为使喷管的最高温度不超过材料允许的温度而能允许的运行时间;(2)在所允许的时间的终了时刻,壁面中的最大温差;(3)在上述时刻壁面中的平均温度梯度与最大温度梯度。
h解:Bi0.7134=0.76921110001750(1)0.43605301750msincos111ln2sincos011Fo0.99932122cFoFo15.5s1(2)(1)maxmmcos110(10001750)(1)293.9Ccos0.76921tth0(3)59451C/mmaxxxxt11xmdx(x)cos()010x0xm1000293.917500(cos1)(cos0.769211)32655C/m10.009无限长圆管3-32对于一无内热源的长圆柱体的非稳态导热问题,在某一瞬间测得r=2cm处温度的瞬间变化率为-0.5K/s。试计算此时此处圆柱体单位长度上的热流量沿半径方向的变化率,43W/(mk)1.2105m2/s并说明热流密度矢量的方向。已知,。解:由无内热源常物性一维非稳态方程式:t1ttr(r)0.5(r)0.5rrt2rrtrr3.14430.0232(r)2(0.5)22510W/m5r1.210225KW/m热流密度矢量指向圆柱的中心。333、已知:一黄铜柱体,d20cm,初温为20C的值,t100C,柱体中心温度在10min内上升到80C.
10952m80100解:由附录5得a3.4310m/s,0.25,c84403772010003a3.4310600F2.06,由附录2图1查得Bi0.4,v22R0.1Bi1090.42h436W/(mK).R0.1623-34已知:一长轴,d170mm,初温为17C,30W/(mK),a6.210m/s,2炉温t850C,h141W/(mK).m求:使长轴的中心温度达到800C所需的时间,及该时刻钢轴表面的温度。hR1410.085850800m解:Bi0.40;0.060,3085017022aR0.085由附录2图1查得F4,F44661s;o206Ra6.210rit850w由1及Bi0.4查附录2图2得0.83.R800850mt8500.8350808.5C.w62335、已知:一长轴,d40cm,初温为600C,22.3W/(mK),a8.810m/s,2t30C,h18.5W/(mK).求:长轴的最低温度达到450C所需的时间。122.3m解:6.03,由附录2图2查得0.923,BihR18.50.204200.737smsm按已知0.737,/0.798.5700.923000s22R0.2由附录2图1查得F0.7,F0.73181.8s53min.006a8.81018.50.220.434911或:Bi0.166,(0.1700)2.78990.3584,0.5987,1122.30.1661.00420.5877(10.9352)1.00420.038101.0423,23J()0.99670.03540.59870.32590.59870.05770.598710.099670.021190.11680.05770.21460.9135.w1.0423e0.3584F00.91350.737e0.3584F00.7370.7740,0.952400.3584F0.2561,F0.2561,F0.715.下同。000336、已知:一钢锭可视为长圆柱体,d600mm,初温为30C,43.5W/(mK),622a7.510m/s,t1400C,h290W/(mK).求:装炉后2h、3h、4h及5h等四个时刻钢锭表面及中心的温度,并画出时间-温度曲线。
6hR2900.3a7.5107200s解:装炉后2h,Bi2,F0.6,0.4602243.5R0.3mm0.3,t14000.3(140030)989C,t14000.138(140030)1211C.ms0同理可算出其他时间的数据,结果列于下表:BF//t,Ct,Ci0smm0ms2h20.60.460.398912113h20.90.460.14120813123h21.20.460.063131413605h21.50.460.0313591381F0.20为画出温度-—时间曲线,需计算数个数下的温度,此处从略。337、已知:一钢锭d500mm,高为800mm,初温为30C,40W/(mK),622a810m/s,t1200C,h180W/(mK).求:3h后再钢锭高400mm处的截面上半径为0.13m处的温度。解:所求之点位于平板的中心截面与无限长圆柱r0.13m的柱面相交处。6hR1800.4a0.81033600对平板:Bi1.8,F0.54,02240R0.4m由图3-6查得0.66;06hR1800.25a0.81033600对圆柱:Bi1.125,F1.38,02240R0.25r0.131m由附录2图1查得0.12,又据0.52,0.889.R0.25Bi0m由附录2图1查得0.885,0.120.8850.1062.m00mm所求点处的无量纲温度为:()()0.660.10620.0701.c00mt0.070112000.0701117012001118C03338、已知:一长塑料棒d30mm,0.3W/(mK),c1050kJ/(mK).2t150C,h8.5W/(mK),3min后,棒表面由初温降到200C。求:棒的初温是多少?0.372hR8.50.015解:a2.8610m/s,B0.425,3ic1050100.37a2.861060twt2FF0.229,Ae10J().022w1R0.015tt0
cBi0.40380.425Aab(1e)1.00420.5877(1e)1.00420.5877(10.8423)1.00420.092681.0969.b1/20.43491/2(a)(0.1700)0.9154,1,1Bi0.42523J()J()abcd10111230.99670.03540.9154(0.3259)0.91540.05770.91540.80030.372hR8.50.015解:a2.8610m/s,B0.425,3ic1050100.3twt2001500.915420.2291.0969e0.80031.09690.82540.80030.7246.ttt150001500.724650500.7246(t150),t219C.000.7246应加热到至少219C.3-39有一耐热玻璃棒,直径为25mm,为改善其表面的机械特性,在表面上涂了一层极薄R0.10mK/W的导热系数很大的金属层。在此金属涂层与芯棒之间平均存在有l的热阻。该棒起初处于均匀温度800K,然后突然被置于300K的气流中冷却,表面传热系数2h120W/(mK),试确定将该棒的中心温度降低到500K所需的时间。玻璃棒物性参数32600kg/mcp808J/(kgK)3.98W/(mk)如下,,。解:当量表面传热系数:"2h(1/hRl)61.78W/mKl"hR61.780.0125Bi0.194020.64396,A1.0484913.98mln()m500300A00.4Fo2.323828003000122RcRFoFo191.75s一维球体340、已知:洋山芋近似看作球,d5cm,初温为20C,物性近似取50C水的值,2烘箱温度t250C,h20W/(mK).求:20min后山芋中心的温度。6210.648解:查附录10得0.648W/(mK),a15.710m/s,1.296.BihR200.0256a15.7101200mF0.301,由附录2图4查得0.7.022R0.0250tt0.72500.7(25020)89C.0
003-41一钢球直径为10cm,初温为250C,后将其置于温度为10C的油浴中。设冷却过程中2200W/(mK)0的表面传热系数可取为,问欲使球心温度降低到150C需要经过多长时间,44.8W/(mk)此时球表面的温度为多少?球的导热系数为,热扩散率为521.22910m/s。hR2000.05解:Bi0.223244.8由近似计算:=0.86265,A1.06831mln()15010Am00.5833Fo0.81283225010012RFo165.3ssin1又0.8805100.88051400.8805123.3CRm0tt123.310133.3CRRf342、已知:滚珠d20mm.初温为300K,50W/(m/K),c500J/(kgK),327800kg/m,t1300K,h5000W/(mK).求:滚珠离开表面1mm深的地方温度达到1000K的时间。150r0.009r解:1,0.9,查附录2图5的0.705,BihR50000.01R0.01m1000-13000.3rm按题意0.3,0.426.300-13000.705m0a5032查附录2图4得F0.449,a1.2810m/s02Rc780050022FR0.4490.0103.51s3a1.2810
343、已知:半球形玻璃r0.15m,初温为300C,0.8W/(m/K),c840J/(kgK),322750kg/m,t410C,平面一侧绝热,球面一侧的表面传热系数h10.5W/(mK).求:8h后半球内的最高温度。10.80.8-72解:0.508,a3.46310m/sBihR10.50.15c2750840-7a3.461036008mrF0.443,查附录2图4、5得0.28,0.45.022R0.150mr0.450.280.126.最高温度为表面温度t4100.126(41030)362C.m344、已知:橘子可近似看作d6cm的圆球,,初温为10C,物性近似取5C水的值2近似计算,t5C,h7W/(mK).求:橘子多长时间结霜。解:橘子外表面的温度应c大于零度,故物性按(100)/25C查取。3210.5630.593W/(mK),a13.410m/s,2.68,BihR70.03tt0(5)5sss查附录2图5得0.84,按已知0.333,tt10(5)15m000.333amss/0.3964,查附录2图4得F1,020.84R00m22FR10.0306716.4s1.87h.8a13.410345、已知:卵石d10cm.初温为20C,2.2W/(m/K),c780J/(kgK),262t80C,h35W/(mK),a1.1310m/s.求:半小时和两小时后,卵石的中心温度及没立方米对方体积的卵石的出热量。a12.2解:(1)半小时后,F0.8136,1.26,02RBihR350.05m查附录2图4得0.24,t800.24(8020)65.6C.查附录2图5得:0ss0.685,0.6850.240.1644,t800.1644(8020)70.1Csm070.165.6球体平均温度可近似地取为两者间的平均值,则67.9C234R故这一段时间中的蓄热量为:1000c(tt)03
343.14160.05710007802496(67.920)4.8810J.3或查附录2图3,得Q/Q0.8,0343.14160.057Q10007802496(8020)6.11310J0377Q0.8Q0.6113100.84.8910J。0am(2)二小时后,F3.254,查附录2图4得0.001702R0s0.00170.6850.00116,t800.00176079.90C,0t800.00166079.904C,平均温度为79.9C,s343.14160.05710007802496(79.902-20)6.1110J.3dd3-46、已知:两个固体球,初温为600K,=300K,A=200mm,B=20mm,31600Kg/mc0.4kJ/(kgK)c1.6kJ/(kgK)170W/(mK)A,A,B,A,221.7W/(mK)h5W/(mK)h50W/(mK)B,A,B.求:把两个球表面冷却到415K及把两球中心冷却到415K所需的时间,并对计算结果作出定性分析。hR50.1解:Bi()0.002940.1,A可用集总参数法。AA170hcV2600-300300K,415-300115K,e,0011535exp(),0.3833exp(0.0002344),30016004000.10.00023440.9589,4091s.hR500.01Bi()0.2940.1,B球应采用图线法或Campo拟合公式。BB1.72F2FAe10f()Ae10,102b10.27791(a)(0.0988)0.9578,1Bi0.294cBi0.01910.2940.9787,Aab(1e)1.00030.9858(1e)1.08861sin(0)m0.97872F0.9579F对球中心,0,f()1,1.0886e01.0886e0,1000.38331.0886e0.9579F0,e0.9579F00.3521,0.9579F1.0438,0
1.762aF1.0897,a2.65610m/s,1.0897.02c4001600Rp261.08970.01/(2.65610)41.03s.sin()sin(0.9897)1对球面上,1,f()f()0.8478,110.989710.38331.08860.8478e0.9579F0,e0.9579F00.4153,0.9579F0.8787,026F0.9137,0.91730.01/(2.65610)34.54s.0A球中心或表面达415K,需4091s;B球中心达到415K,需41.03s,表面需34.54s。温度与时间定性分析图如下:3-47.在温度为-30℃的高空云层中形成了直径为5mm的球状冰雹,然后开始落下并穿过温度为5℃的热空气层.试计算冰雹需落下多少时间其表面才开始熔化,并确定此时冰雹中心2h240WmK,c2040JkgK的温度.冰雹的物性可取冰的值,即取.半无限大物体3-48一种测量导热系数的瞬态法是基于半无限大物体的导热过程而设计的。设有一块厚材00料,初温为30C,然后其一侧表面突然与温度为100C的沸水相接触。在离开此表面10mm302200kg/m处由热电偶测得2min后该处的温度为65C。已知材料的,c700J/(kgK),试计算该材料的导热系数。000解:t100C,t30C,x0.01m,t65Cw03260120s,2200Kg/m,C700J/KgK651000.5erfn由参考文献:=0.477301000x由=222cx22007000.01c1.41W/mK22441200.47703-49、已知:有两个很大的不锈钢制及木制的家具,初温为20C。木制的物性可取为3545kgm/0.17W/mKc2385/JkgK,及;不锈钢的物性可取为
37820kgm/18W/mKc460/JkgK,及。求:用定量分析说明用手去触摸他们时,哪一个感觉更冷一些?解:温度不同的两种物体接触时界面上要保持热流连续及温度连续,如图所示有:dT12dTT1T212dx12dx,近似地以x1,x2代TT2212xx替导数,则有:12,另一方面,xx在1中物体1放出之热应等于2中物体吸收之热,则有:TTTT1212cxcx11122222,其中2,2为平均温升或温降,将以上二式结合得:22111cT1222cT2,即:T122c2T2111cTT如果接触处温度0接近1,则人体感觉不是很凉;TT如果接触处温度0接近2,则人体感觉就凉。c54523850.17470.0对于木材222;c10000.61841741606对于人体111c7820460188047对于木材222。T470.0T8047110.2935.01T1606T1606所以木材:2;不锈钢2。0因而人手与20C木材及钢接触时,人的皮肤温度完全不同,对于木材下降不多;而对于不锈钢则大幅度下降。02300kgm/31.4W/mK3-50、已知:夏天高速公路初温为50C,,及c880/JkgK0C,突然一阵雷雨把路面冷却到20并保持不变,雷雨持续了10min。求:此降雨期间单位面积上所放出的热量。作为一种估算,假设公路路面以下相当厚的一层0混凝土上均为50C,分析这一假设对计算得到的放热量的影响。106q2ctwt0223008801.45020解:3.142191.08283360030139.6KJ。夏天路面以下温度实际上低于表面温度,因而这一假设使计算得到的值偏高。3-51、已知:要在寒冷地区埋设水管,把地球简化成半无限大的物体,冬天用较长时间内地球表面突然处于较低的平均温度这样一种物理过程来模拟。某处地层的7200a1.6510m/s,地球表面温度由原来均与的15C突然下降到-20C,并达50天之久。
求:估算为使埋管上不出现霜冻而必须的最浅埋设深度。解:埋管的深度应使五十天后该处的温度仍大于等于零度。tx,tx020x0.57140.56因而得tt0x1520,由误差函数表查得2a,2所以x20.26a20.561.6510502436000.946m。03-52、已知:医学知识告诉我们:人体组织的温度等于,高于48C的时间不能超过10s,否则该组织内的细胞就会死亡。今有一劳动保护部门需要获得这样的资料,即人体表面接触00000到60C、70C、80C、90C、100C的热表面厚,皮肤下烧伤程度随时间而变化的情0况。人体组织性取37C水的数值,计算的最大时间为5min,假设一接触到热表面,人体表面温度就上升到了热表面的温度。求:用非稳态导热理论做出上述烧伤深度随时间变化的曲线。082解:按半无限大物体处理,37C时a15.1810m/s。利用习题54中给出的公式,xxerf可得2a之值,由误差函数表可查得相应的2a的数值,从而确定不同(单位00CtC600C秒)下温度为48的地点的x值,即皮下烧伤深度。令对于x及70两种情形给出计算结果如下:烧伤深度,mm0tx,txxtC,xtt20xa0.5分1分2分3分4分5分钟钟钟钟钟钟600.521740.501420143.034.285.246.056.77700.666660.68522.924.145.857.168.279.25变化曲线略。3-53.70℃的热茶突然倒入初温为25℃的陶瓷茶杯中.茶杯壁面厚6mm.假设茶杯内表面温度立即上升到70℃,试确定茶杯内表面下2mm处温度达30℃所需的时间.陶瓷材料的72a410ms热扩散率.多维非稳态导热30.65W/(mK),810kg/m,3-54、已知:一正方形人造木块,边长为0.1m,
2c2550J/(kgK),Ct425C,h6.5W/(mK),初温为25,经过4小时50分24秒后,木块局部地区开始着火。求:此种材料的着火温度。解:木块温度最高处位在角顶,这是三块无限大平板相交处。h6.50.05sBi0.50.1;由图3-7查得0.8,0.65m70.6572a3.1471017424a3.14710m/s,F2.19;o22c8102550R0.05mssm由图3-6查得0.4,0.80.410.328.00m0s33角顶处无量纲温度:()0.3280.0353,00角顶温度:tt0.0353(tt)4250.0353(25425)411C.030C3-55、已知:一易拉罐饮料,初温为,物性可按水处理,罐的直径为50mm,高为120mm,2t5Ch10W/(mK).罐壳的热阻可以忽略,罐中的饮料的自然对流可以忽略。,10C求:饮料到达所需的时间。301020C2解:物性按计,则有820.599W/(mK),a14.310m/s,h100.061hR100.0251B1.002,B1.0,B0.417,B2.4.iiicic0.5990.59952F30525C,1055C,0.2,Ae10.025002b10.91881对平板:(a)(0.4022)0.7580,1Bi1.002cBi0.42711.002Aab(1e)1.01010.2575(1e)1.0998,52F30525C,1055C,0.2,Ae10.025002b10.43491对柱体:(a)(0.1700)0.8245,1Bi0.417cAab(1ecBic)1.00420.5877(1e0.42380.417)1.0953,
aa2222F,F,0.060.0036,R0.0250.000625.0202R0.0036FF5.76F,于是有:0000.000625Fm(m)(m)1.2046e0,c0000.2e5.3071F00.1660,1.78565.5071F,F0.324,001.2046280.3240.06/(14.310)8162.65s2.27h.3-56一直径为0.15m,高0.05m的平板玻璃圆盘,送入退火炉中消除应力,其初始温度为0030C,炉中温度为450C。设玻璃盘在炉内各时各表面均可受到加热,表面传热系数为29.5W/(mK)0。按工艺要求,需加热到盘内各点温度均为400C以上,试估算所需时间。30.78W/(mk)2700kg/mc835J/(kgK)已知该盘导热系数,,。解:平板玻璃盘在几何上是直径为0.15m的圆柱与厚为0.05m的无限大平板相交而成0按加热工艺要求,使最低温度即中心温度达到400C10.78对平板:3.284Bih9.50.02510.78对圆柱:==1.095Bih9.50.075400450m按题意:0.11930450o采用试凑法求解,取一组值,计算每个值下/值,由此确定所需的时间m0mmm其中(Fo),(Fo),p2c2Roopocmmmt(min)(Fo)(Fo)pcopoco1504.9820.5540.300.570.1711605.3140.5900.280.500.1401705.6460.6270.250.460.115由此可见,大约170min(2.8h)后可达到要求。357、已知:牛肉尺寸为40mm60mm100mm,初温为5C,牛肉的物性可按水处理,2t180C,h20W/(mK).求:把牛肉加热到80C所需要的时间。解:这是三块平板相交的问题,要计算使中心温度达到80C所需的时间,牛肉按5808242.5C计算,查得物性:0.638W/(mK),a15.010m/s2
h200.02xB0.62696ix0.638hy200.03B0.94044iy0.638h200.05zB1.5674iz0.638100m2F175C,100C,0.5714286,Ae1001750020.918810.91881对平板x(轴向),(0.4022)(0.4022)0.535421B0.62696icBi0.427180.62696Aab(1e)1.01010.2575(1e)1.070592.120.91881对平板y,(0.4022)0.725064,20.940440.427180.94044A1.01010.2575(1e)1.09528.220.91881对平板z,(0.4022)1.01174,31.56740.427181.5674A1.01010.2575(1e)1.13576.2aaaF,F,F,F0.4444F,F0.16F,0x20y20z20y0x0z0xxyzm(m)(m)(m)0.5714e1.01935F0x0.4291F0.83xyz0x000080.830.0004/(1510)2213s37min.3-58、已知:一短钢圆柱体,直径为10cm、高10cm,初温-6147.59.5510180解:对无限长圆柱体:3.8,Fo0.688,22BihR2500.050.05mss查附录2图1得0.71,由附录2图2查得0.88,0.880.710.625omo对无限长平板:-6147.59.55101800.5,3.8,Fo0.688,22BihR2500.050.05mss由图3-6查得0.9,由图3-7查得0.88,0.880.90.792omosss短圆柱体中的最低温度为()()0.6250.7920.495.cooott0.495(tt)143.9C;f0fmmm最高温度为()()0.710.90.639,cooott0.639(tt)177C,t177143.933.1C.f0f3-59、已知:对于3-5节中所讨论的长棱柱体的非稳态导热问题(图3-14a),假设平板p1
及p2从过程开始到t时刻的换热量与该平板在这一非稳态导热过程中的最大换热量之比分别为Q/Q及Q/Q.0p10p2Q/Q0求:导出用上述两个值表示的在同一时间间隔内柱体的之值的计算式。解:对一维问题按式(3-34)有:1tt2111()1()dV1dx1dx,10101Vtt2100111tt2112()1()dV1dx1dy,20202Vtt210022据乘积解法,于是有对二维方柱体121tt2111()1()dV1dx1dx,10101Vtt2100114121121dxdy1dxdy0102010222121211121(dx)(dy)010212111211121dx1dy1dx1dy01020102121200001212其中均可据式(3-34)算出。0012综合分析0623-60、已知:一大型加热炉炉底厚50mm,初温为25C,a510m/s,024.0W/mKtC1600h40W/mK,点火后,。按工艺要求炉内各表面0均应加热到1500C方可投入使用。求:从开始点火到满足这一条件所需的时间。解:近似地认为炉底外表面是绝热的,则这是一厚为220.05m的无限大平板的非稳态导热问题。140.82.0Bih400.05,由图3-7查得m,m147516000.07940tC1600100/0.81475251600m。0,6.10.0530500sh8.471由图3-6查得Fo6.1,即510。3-61、已知:半无限大物体分别处于下列三种边界条件:
tq(1)第一类边界条件,w为常数;(2)第二类边界条件,w为常数;(3)第三类边界条t件,h及为常数。求:定性地画出物体中的温度随时间变化的曲线。解:dm1mm43W/mK3-62、已知:一输油管,外径0,壁厚45,外侧绝热,,2a1.1710x52m/s0C0Ch400W/mK,初温为-20。然后80的油突然流经该管,。求:(1)输油5min后油管外表面的温度;(2)输油5min后油管内表面的瞬时热流密度;(3)输油5min后油管单位长度上所吸收的热量。解:假设按无限大平板处理,如图所示:45mm,5a1.1710560Fo1.733220.045,h4000.045Bi0.41943,x0油管外表面处。采用拟合公式m2FoAe1f10,112b0.9188a0.40220.385351Bi0.419,Bi0.42710.41910.6208,Aab1e1.01010.25751e1.0523。f11coscos01。2FoxAe1cos1(1)0,
0.620817332m1.0523ee所以0,t80m0.539602080,tCm800.5396。x22Fox11Fo|Ae11sinAesinx0101x(2),t2Fo1qAe1sin01xx0.66790.620843e=0.0452=431001.05230.51280.581913.79618627KWm。186270tC46.60tC8046.6相应温差400,w>26.04。12Ae1FoB(3)00,,acBi1.00630.34830.419B0.93721bBi,10.54750.41910.5057所以1.05230.51280.9372,0,0.4943000.4943cVtt0.4943c120800.4943=a60.49433.67510=7=2.56510J。33-63、已知:一固体球,d10mm,3200kgm,18W,c1200/854Jt250J,初温为450,然后进行两步冷却:第一步,C,2h100Ct250W,球的中心温度降到350;第二步,C,2h60000CW,球的中心温度降到50。求:每一阶段冷却所需时间及该阶段中球体所释放出的热量。解:
温度计算hR100.0053Bi2.77710第一阶段,18<<0.1,可用集总参数法。hFhFh1h610631.562510cV0e,cVcVF/cd120032000.01,t2535025mm0.7647345025450250.7647e1.5625100,所以,0.268333100.171710171.7s30.26831.562510,1.5625t255025mm0.07692第二阶段,04502545025,hR60000.005m2FoAe1fBi1.667118,0,Bi0.31912.667Aab1e1.00030.98581e1.00030.985810.58751.4069=,112b0.2779a0.09883.76641Bi1.667,11.94070f11,,,m3.7663Fo0.076921.4069e所以0,2.5650.3414Fo0.77172.5650.34143.7663Fo,3.7663,2a18/320012000.0050.7717Fo0.77174.12s226R0.005,4.687510。换热量计算第一阶段:33d3.140.01Q10ctt32001200450350201J66第二阶段:
Q212QAe1FoB0,,acBi1.02950.19531.6671.02950.3256B0.65141bBi10.68411.66711.0804,3.7663Fo1.4096e0.6514,3.76630.77171.4096e0.65141.40960.065140.65140.04968,3dQ2Q010.049680.9503Q00.9503c35025633.140.010.9503320012003250.9503653.12621J=6。00作为一种验算,比较上述换热量与球从450C降温到25C所释放的热量:36d3.141000Q0c4502532001200425854J从450C25C,66。QQ201621822J854J12<。t3-64、已知:一二维的矩形区域,初温为0,然后其四个表面突然受到均匀的热流密度q的加热。证明:该矩形区域中非稳态导热的过余温度场可以用两个相应的一维非稳态导热问题过余温度场的叠加来获得。解:参见陶文铨编著《数值传热学》(第一版,西安交通大学出版社,1998)第90~92页。3-65.在一太阳能储能系统中有一卵石蓄热床,卵石的平均直径为60mm,初始温度为350℃,后温度为280℃的冷空气流经该蓄热床.试确定需经过多长时间与冷空气接触的第一排卵石1.6WmK能释放用于加热空气的能量的90%?卵石的导热系数,热扩散率72a710ms.3-66、已知:物体的非稳态导热进入正规状况阶段后,一般定义同一点上两个不同时刻的过lnln12m余温度1、2与相应时刻1、2的关系21为冷却或加热速率。求:对无限大平板导出m的表达式,并利用表3-1所提供的信息。设计出一种测定非金属固体材料(如塑料版等)的导温系数的简易方法。解:对无限大平板,据式(3-22)在进入充分发展阶段后有:x,2sin14Foxe1cos101sin1cos1,2sin1xABcos1记11,(1)sin(1)cos(1),,则可见以上表达式中A、B两部分仅与Bi数及位置有关,对平板中的固定位置,A、B为常数(在一定Bi下),a2a21x,122CeCe设记CAB,则有0。两边取对数:2a1lnxC,ln0ln212、,在同一位置x,在两个时刻进行温度测定:
22aa11lnxC,1ln1ln0ln21lnxC,2ln2ln0ln22,。221a2alnln12ln1ln2221m1a22所以,,121,h与Bi=1有关,对非金属固体,一般在10以下,设法使流体(液体如水)发生对流11.5707换热,则可以获得很大Bi数的情况,此时2,于是22ln12ln22ln12ln2a21,21,通过实验测定的简易方法如下。将试件制成一块大平板。先将试件在恒温炉中加热到一定温度,随后放入恒温槽中,如图示。为强化换热用搅拌器对流进行搅拌,同时也有利于建立一个均匀的温度场。在试件中固定位置装入一个热电偶的终点,另一个结点用于测量环境温度,由温差热电偶的读书即可得被测点处的过余温度。测定两个不同时刻的值后即可据上式计算a之值。3-67、已知:一直径为d的钢球加热到ts0温度后,被突然置于温度为tf0的液体中冷却。由于液体的容积有限,在钢球冷却过程中,液体也逐渐升温。为强化钢球表面与液体之间的换热过程,液体槽中加了搅拌器,因而可以近似地认为任一槽间夜槽中的温度是均匀的。表面传热系数为常数。求:导出确定钢球温度及油温随时间变化的微分方程式,并求解之。tt及解:假设容器的外壁绝热良好,而且可按集总参数法处理。记钢球的温度分别为sf,则可列出下列两个微分方程:dthFdtffhFssttttfssf钢球:dxsVc;液体:dfxVcff,其中下标sf、分别表示钢球及液体。hFhFfAsB记sssVc,fsVcff,则可得如下联立方程组:dtsAtAtsfd(1);dtfBtAtfsd(2)。0,ttt,t初始条件为ss00ff。
1dtsttfs由式(1)得Ad,代入(2)得下列二阶微分方程:dt2dtdtssf2(AB)0,0,tts0,Atf0ts0ddd。()ABtcce解此二阶常微分方程得s12。AAc1ts0tf0ts0,c2(tf0ts0)由两个初始条件可得ABAB。A()ABtt(tt)1ess0f0s0AB最后得:;B()ABtt()ttABefs0f0s0AB。小论文题目3-68、已知:如果非稳态导热的求解仅着眼于正规化状况阶段(即充分发展阶段),则对于无限大平板、无限长圆柱及球,其温度的微分方程可简化为一个常微分方程。定义无量纲温tt1ttdVttbVV度为b,其中,为容积平均温度。求:对两侧对称受热(冷却)的无限大平板导出的微分方程及边界条件。2tta2解:厚为2的无限大平板的一维非稳态导热方程为:x(1)ttx0,0;x,htt边界条件为:xx(2)tx,在导热进入正轨状态(充分发展阶段)时,仍为的函数,热而无量纲过余温度ttttxb则仅为的函数而与时间无关,1ttdVbV其中V,为容积平均温度。tttdtbtfx,(tht)ttd据此bb,22tdtdtbbt,22ttxdxxdx,代入式(1)得:2dtbtdatbt2ddx,222dddtbbt1dtt或222dxdatbbtdx/attd,1d22dtbt22其中dx/仅与x有关,atbtd仅与有关,1dtbt0ttd又因为b,为使保证正值,故加上负号,于是得:
2dttdd21b020ttdaL/2dxL/dX2b,为特征值,,,ddhdXX0,0;1,Bi边界条件则为:dXdX,即dX。tt及3-69、已知:两个很大的金属块,初温均匀并各为bc,然后突然在一侧表面上将它们紧密接触,不存在接触热阻。tbtbcts求证:界面温度为1b,其中ac12111bac21222。证明:如图所示,设两物体间的接触热阻略而不计,则界面上的温度连续要求在任一时刻,而表面的温度必相ttttt等,记为s,而且bsc,同时这一温度s在接触开始瞬间即已形成且不会随时间而变,如图所示。因而物体1、2中的温度均可3-5的公式(3-52)计算,界面上的热流连续要求下式成立:ttttccbssc111111ttt/112aasbccc12,由此可得到:222222。3-70、已知:同上题,但接触面上存在恒定的接触热阻2RmKWs/。坐标的选取如图所示。求:两个半无限大物体非稳态导热的控制方程、边界条件。1hsttRR解:设12(初始时间)接触热阻为s,令s,t1ht()ts21则界面上应有以下条件成立:x,tt1212xx12。两个控制方程为:22tttt1122a,a,x0,0tt;x,tt122211102220xx12。
'
您可能关注的文档
- 《会计学导论》习题及答案.doc
- 《传感器》第四版唐文彦习题答案.doc
- 《传感器与检测技术》试题及答案 大集合.doc
- 《传感器与自动检测技术》习题解答.doc
- 《传感器与自动检测技术》课后习题解答.doc
- 《传感器原理及工程应用》第四版(郁有文)课后答案.doc
- 《传感器原理及应用》课后答案.doc
- 《传播学教程》课后习题答案-41p.doc
- 《传播理论:起源、方法与应用》(第5版)课后习题详解.pdf
- 《传统文化与法制中国》测试题满分答案.docx
- 《传统文化与法制中国》真题(附答案).doc
- 《低碳经济》试题答案合集 扬州市专业技术人员.docx
- 《低碳经济与幸福指数》练习题及参考答案.doc
- 《低碳经济循环经济与加快经济发展方式转变》考试题库及参考答案.doc
- 《供配电技术》唐志平第三版习题答案(全).doc
- 《保险会计》习题及答案.doc
- 《保险学教程》各章练习题答案.doc
- 《保险学概论》练习题及答案大全.doc