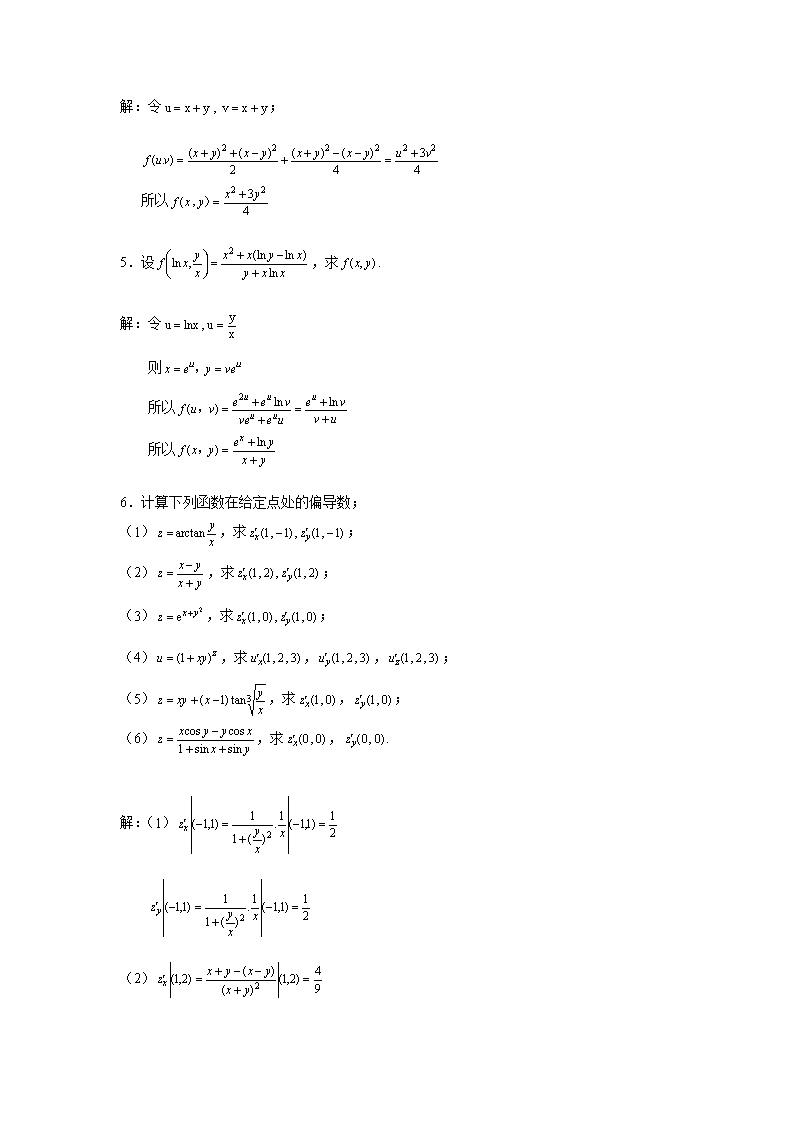- 1.97 MB
- 2022-04-29 14:08:21 发布
- 1、本文档共5页,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,可选择认领,认领后既往收益都归您。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细先通过免费阅读内容等途径辨别内容交易风险。如存在严重挂羊头卖狗肉之情形,可联系本站下载客服投诉处理。
- 文档侵权举报电话:19940600175。
'《微积分》(中国商业出版社 经管类)课后习题答案习题七(A)1.在空间直角坐标系中,下列方程表示什么形状的图形.(1)(2)(3)(4)(5)(6)(7)(8)解:(1)旋转抛物面.(2)以(1,2,0)为原点为半径的球面.(3)抛物线柱.(4)以为中心的椭球面.(5)旋转抛物面.(6)圆锥面.(7)一个点(8)双曲抛物面.2.给定两点,,求(1)与之间距离;(2)线段的垂直平分面的方程;(3)以为中心,为半径的球面方程.解:(1).
(2)中点;垂直向量;方程为:.(3).3.求下列函数定义域,并画出定义域示意图.(1)(2)(3)(4)(5)(6)(7)(8)解:(1)(2)定义域:(3)(4)(5)(6)(7)且(8)4.设,求
解:令;所以5.设,求.解:令则所以所以6.计算下列函数在给定点处的偏导数;(1),求;(2),求;(3),求;(4),求,,;(5),求,;(6),求,.解:(1)(2)
(3)(4)(5)(6)7.求下列函数的一阶偏导数(1)(2)(3)(4)(5)(6)(7)(8)解:(1)(2)
(3)(4)(5)(6)(7)(8)
8.设,验证方程解:证明:9.设,可导,验证方程解:证明:10.设,验证方程解:证明:11.设,其中为可微函数,验证方程解:证明:12.设,验证方程解:
证明:13.求下列函数的二阶编导数(1)(2)(3)(4)(5)(5)解:(1)(2)(3)(4)(5)(6)14.求下列函数的全微分(1)(2)(3)(4)(5)(6)(7)(8)
(9)(10)(11)(12)解:(1)(2)(3)(4)(5)(6)(7)(8)(9)(10)(11)(12)
15.求下列函数在给定点的全微分(1)(2)(3),(4)解:(1)当,时.(2)当,时.(3)当,时.;当,时(4)当,时.16.求函数在点(2,1)当,时的全增量和全微分.解:17.求函数在给定点与给定,的全微分(1)点(0,1),,;
(2)点(1,0),,.解:(1)(2)18.用全微分求下列各数的近似值.(1)(2)解:(1)令令,,,,(2)令令,,,所以19.已知一长为8米,宽为6米的矩形,当宽增加5厘米,长减少10厘米时,求矩形对角线长度变化的近似值.8610解:设长为,宽为对角线长.
20.用圆锥体形变时,它的底半径R由30厘米增到30.1厘米,高h由60厘米减到59.5厘米,试求体积变化的近似值.解:令体积,,,变后的体积21.用水泥做一个长方形无盖水池,其外形长5米,宽4米,深3米,侧面和底均厚20厘米,求所需水泥的精确值和近似值.解:精确值近似值22.求下列复合函数的偏导数或全导数(1),,,求;(2),,求;(3),而,,求;(4),,,求,;
(5),,,求,;(6),,,求,;(7),,,求,;(8),,,求.解:(1)(2)(3)(4)(5)(6)(7)
(8)23.,可微,求,.解:令则24.,可微,求,.解:令25.设,求.解:26.设,求.解:
27.设,其中可微,求.解:令28.设,其中可微,而,证明.解:证明:29.设,且可微,证明.解:证明:30.设,其中可微,求,.解:令,则
31.,,,求.解:32.设,求,其中有二阶编导数.解:33.已知,,,且的二阶偏导数都连续,求.解:34.设具有二阶连续偏导数,且满足,又求.
解:令35.设,其中为可微函数,求.解:36.已知,,其中是和的函数,求证解:对等式两边分别微分得:同理可得:两式相乘得:37.设函数有连续偏导数,且由方程所确定,求.解:所以
38.求下列方程所确定的隐函数的导数(1)(2)(3)(4)解:(1)(2)令则(3)令则(4)令则39.求下列方程所确定的隐函数的全微分(1)(2)(3)(4)解:(1)令则所以(2)令
则所以(3)令(4)令所以40.求下列函数的极值,并判断是极大值还是极小值(1)(2)(3)(4)(5)(6)(7)(8)
解:(1)令,因为所以又因为所以(1,0)是极小值。(2)令,因为所以又因为所以(1,1)是极小值(3)令因为所以又因为所以极大值(4)令因为所以当,时而所以而当,时无极限。(5)
因为所以而所以(6)令因为所以,且所以(7)令因为因为,且所以(8)令.当,时,且时,,但,所以。当时,因为,所以无极值。
当时,因为所以无极值。当,或时,无极值。41.求下列函数在指定条件下的极值(1)(2)(3)解:(1)令即又因为(2)令即又因为(3)令即又因为所以42.设某工厂生产甲、乙两种产品,产量分别为和(单位:千件),利润函数为已知生产这两种产品时,每千件产品均需消耗某种原料2000公斤,现有该原料12000公斤,问两种产品各生产多少千件时,总利润最大?最大利润为多少?
解:设分别生产4件,令则即又因为所以所以当分别生产3.8件和2.24件时利润最大为22.2万元。43.某地区生产出口服装和家用电器,由以往的经验得知,欲使这两类产品的产量分别增加单位和单位,需分别增加和单位的投资,这时出口的销售总收入将增加单位.现该地区用单位的资金投给服装工业和家用电器工业,问如何分配这单位资金,才能使出口总收入增加最大?最大增量为多少?解:令,设分别投入单位和单位令则又因为所以,所以当分别分配单位和单位时总收入增加最大为44.设生产某种产品必须投入两种要素,和分别为两种要素的投入量,Q为产出量;若生产函数为,其中,为正常数,且.假设两种要素的价格分别为和,试问:当产出量为12时,两要素各投入多少,可以使得投入总费用最小?解:6,则
代入总费用令则45.假设某企业在两个相互分割的市场上出售同一种产品,两个市场的需求函数分别是,其中和分别表示该产品在两个市场的价格(单位:万元/吨),和分别表示该产品在两个市场的销售量(即需求量,单位:吨),并且该企业生产这种产品的总成本函数是,其中表示该产品在两个市场的销售总量,即.(1)如果该企业实行价格差别策略,试确定两个市场上该产品的销售量和价格,使该企业获得最大利润。(2)如果该企业实行价格无差异策略,试确定两个市场上该产品的销售量及其统一价格,使该企业的总利润最大化;并比较两种价格策略下的总利润大小.解:(1)利润所以当,;时(2)利润设则所以所以当时,46.将二重积分按两种顺序化成累次积分,其中
是由下列曲线或直线围成的区域:(1);(2);(3);(4);(5);(6);(7)在第一象限;(8)解:(1)(2)(3)(4)(5)(6)(7)(8)
47.交换下列积分的次序(1)(2)(3)(4)(5)(6)(7)(8)(9)解:(1)(2)(3)(4)(5)(6)(7)(8)
(9)48.计算下列二重积分(1)(2)(3)(4)解:(1)(2)(3)令则有(4)49.计算下列给定区域内的二重积分:(1)由和所围成;(2)由和所围成;(3)由所围成;(4)由所围成;(5)由所围成;
(6)由所围成;(7)由所围成;(8)由围成;(9)由所围成;(10)由所围在第一象限;(11)由所围成;(12)由所围成;(13)由所围成;(14)由所围成;(15)由所围成;(16)解:(1)(2)(3)(4)
(5)(6)(7)(8)(9)(10)(11)解:积分区域如右图阴影部分
01y1x(12)积分区域如图所示:ba0由得:从而令(13)
(14)(15)(16)50.交换积分次序计算下列积分(1)(2)(3)(4)解:(1)(2)(3)(4)51.设求,其中解:当
52.利用极坐标计算下列二重积分(1)由围成,且;(2);(3);(4)解:(1)令(2)令(3)令(4)令53.设,求.解:54.计算,其中D:解:令(B)
1.选择题(1)函数在点的某邻域内偏导数存在且连续是在该点处可微的().A.必要条件,但不是充分条件B.充分条件,但不是必要条件C.充分必要条件D.既不是充分条件,也不是必要条件(2)已知为某一函数的全微分,则的值分别为().A.-2和2B.2和-2C.-3和3D.3和-3(3)求函数,有,且则=().A.B.C.D.(4)已知函数的全微分则=().A.B.C.D.(5)函数的极限情况是().A.无极值B.有有限个极值C.有无穷多个极大值D.有无穷多个极小值(6)已知为函数的极小值,则的值分别为().A.1,1,4,10B.-1,-1,-4,-10C.1,1,-4,-10D.-1,-1,4,10(7)的值(),其中A.0B.0C.D.以上都不对(8)累次积分可以写成().A.B.C.D.
(9)设连续,且,其中是由所围区域,则等于().A.B.C.D.解:(1)B可导可微,但可微不能推出可导。(2)(3)B将答案代入条件中,(4)由题知:则选(5)(6)令选(7)A(8)由题知:选(9)当代入选2.证明下列函数为齐次函数,并说明各为几次齐次函数(齐次函数的概念见§7.5例9)(1)(2)
(3)(4)解:(1)证明:所以是4次齐次函数。(2)证明:所以是次齐次函数。(3)证明:所以是次齐次函数。(4)证明:所以是次齐次函数。3.求下列二元函数的极限(1)(2)(3)(4)(5)(6)解:(1)令则(2)=(3)
(4)(5)(6)令4.证明:当时,极限不存在.解:令则因极限值与有关,即沿不同抛物线趋向于坐标原点时,有不同极限值,所以原极限不存在。5.设,求.解:6.设函数,方程确定是的函数,其中可微;连续,且,求解:令且
则7.求下列各题近似值(1)(2)解:(1)令(2)8.已知,求解:9.设有连续偏导数,和分别由方程和所确定,求解:由
由10.函数由方程所确定,证明解:知11.函数由方程所确定,证明解:
12.求下列函数的最值(1)(2)(3)解:(1)令则求出存在极大值对于端点,当时,取时存在极值当时,取时存在极值所以的最值是,(2)即当时,(3)令对于端点,所以对于端点存在13.计算二重积分,其中
解:令所以14.计算二重积分,其中解:令15.设闭区域为上的连续函数,且求解:令令则所以
所以16.计算积分解:令17.计算下列二重积分(1),其中(2),其中(3),其中由四条直线所围成.解:(1)(2)
(3)18.计算解:19.计算二重积分解:'
您可能关注的文档
- 《微机原理与接口技术》习题答案.doc
- 《微机原理与接口技术》洪永强课后习题集 第2版.doc
- 微机原理与接口技术》洪永强课后习题集__第2版.pdf
- 《微机原理与接口技术》课后习题答案.doc
- 《微机原理与接口技术》课程考试复习题集含答案.doc
- 《微机原理及接口技术》(第2版)—习题解答.doc
- 《微波技术与微波电路》课后答案-华南理工大学.pdf
- 《微生物学》课后习题集.docx
- 《微生物学检验》复习思考题参考答案(1).doc
- 《微积分》(中国商业出版社 经管类)课后习题答案六.doc
- 《微积分》各章习题及详细答案.doc
- 《微观经济学》习题答案 - 梁悦&刘方军.pdf
- 《微观经济学》陈钊,陆明思考题及课后习题答案(完整版).doc
- 《心理咨询师(基础知识)》 复习题 及参考答案.doc
- 《思想道德修养与法律基础》复习试题及答案汇总[1].doc
- 《思想道德修养与法律基础》复习题库及答案.doc
- 《思想道德修养和法律基础及答案》综合测验题库.doc
- 《感测技术基础》(第四版)习题解答.docx