- 1.02 MB
- 2022-04-29 13:59:18 发布
- 1、本文档共5页,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,可选择认领,认领后既往收益都归您。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细先通过免费阅读内容等途径辨别内容交易风险。如存在严重挂羊头卖狗肉之情形,可联系本站下载客服投诉处理。
- 文档侵权举报电话:19940600175。
'20┑┒每一个男子全都有过这样的两个女人,至少两个。娶了红玫瑰,久而久之,红的变了墙上的一抹蚊子血,白的还是床前明月光。娶了白玫瑰,白的便是衣服上的一粒饭粘子,红的却是心口上的一颗朱砂痣。—《红玫瑰与白玫瑰》习题1.1解答1.将一枚均匀的硬币抛两次,事件分别表示“第一次出现正面”,“两次出现同一面”,“至少有一次出现正面”。试写出样本空间及事件中的样本点。解:(正,正),(正,反),(反,正),(反,反)(正,正),(正,反);(正,正),(反,反)(正,正),(正,反),(反,正)2.在掷两颗骰子的试验中,事件分别表示“点数之和为偶数”,“点数之和小于5”,“点数相等”,“至少有一颗骰子的点数为3”。试写出样本空间及事件中的样本点。解:;;;;;3.以分别表示某城市居民订阅日报、晚报和体育报。试用表示以下事件:(1)只订阅日报;(2)只订日报和晚报;(3)只订一种报;(4)正好订两种报;(5)至少订阅一种报;(6)不订阅任何报;(7)至多订阅一种报;(8)三种报纸都订阅;(9)三种报纸不全订阅。解:(1);(2);(3);(4);(5);(6);(7)或(8);(9)4.甲、乙、丙三人各射击一次,事件分别表示甲、乙、丙射中。试说明下列事件所表示的结果:,,,,,.
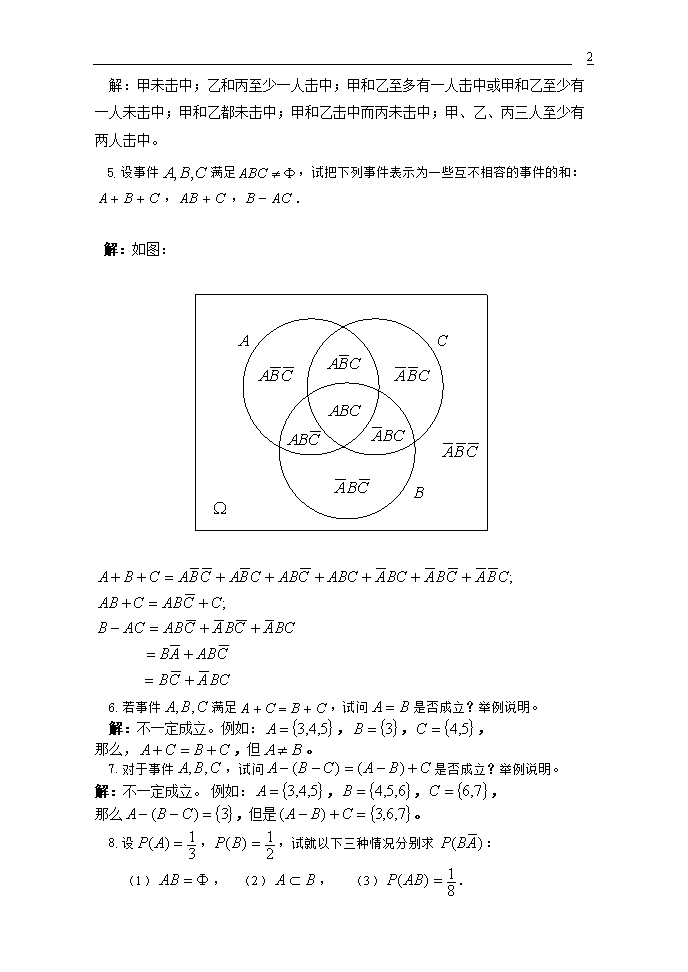
20解:甲未击中;乙和丙至少一人击中;甲和乙至多有一人击中或甲和乙至少有一人未击中;甲和乙都未击中;甲和乙击中而丙未击中;甲、乙、丙三人至少有两人击中。5.设事件满足,试把下列事件表示为一些互不相容的事件的和:,,.解:如图:6.若事件满足,试问是否成立?举例说明。解:不一定成立。例如:,,,那么,,但。7.对于事件,试问是否成立?举例说明。解:不一定成立。例如:,,,那么,但是。8.设,,试就以下三种情况分别求:(1),(2),(3).
20解:(1);(2);(3)。9.已知,,求事件全不发生的概率。解:=10.每个路口有红、绿、黄三色指示灯,假设各色灯的开闭是等可能的。一个人骑车经过三个路口,试求下列事件的概率:“三个都是红灯”=“全红”;“全绿”;“全黄”;“无红”;“无绿”;“三次颜色相同”;“颜色全不相同”;“颜色不全相同”。解:;;;;.11.设一批产品共100件,其中98件正品,2件次品,从中任意抽取3件(分三种情况:一次拿3件;每次拿1件,取后放回拿3次;每次拿1件,取后不放回拿3次),试求:(1)取出的3件中恰有1件是次品的概率;(2)取出的3件中至少有1件是次品的概率。解:一次拿3件:(1);(2);每次拿一件,取后放回,拿3次:(1);(2);每次拿一件,取后不放回,拿3次:
20(1);(2)12.从中任意选出3个不同的数字,试求下列事件的概率:,。解:;或13.从中任意选出4个不同的数字,计算它们能组成一个4位偶数的概率。解:14.一个宿舍中住有6位同学,计算下列事件的概率:(1)6人中至少有1人生日在10月份;(2)6人中恰有4人生日在10月份;(3)6人中恰有4人生日在同一月份;解:(1);(2);(3)15.从一副扑克牌(52张)任取3张(不重复),计算取出的3张牌中至少有2张花色相同的概率。解:或
20习题1.2解答1.假设一批产品中一、二、三等品各占60%,30%、10%,从中任取一件,结果不是三等品,求取到的是一等品的概率。解:令“取到的是等品”,。2.设10件产品中有4件不合格品,从中任取2件,已知所取2件产品中有1件不合格品,求另一件也是不合格品的概率。解:令“两件中至少有一件不合格”,“两件都不合格”3.为了防止意外,在矿内同时装有两种报警系统I和II。两种报警系统单独使用时,系统I和II有效的概率分别0.92和0.93,在系统I失灵的条件下,系统II仍有效的概率为0.85,求(1)两种报警系统I和II都有效的概率;(2)系统II失灵而系统I有效的概率;(3)在系统II失灵的条件下,系统I仍有效的概率。解:令“系统(Ⅰ)有效”,“系统(Ⅱ)有效”则(1)(2)(3)4.设,证明事件与独立的充要条件是证::与独立,与也独立。
20:又而由题设即,故与独立。5.设事件与相互独立,两个事件只有发生的概率与只有发生的概率都是,求和.解:,又与独立即。6.证明若>0,>0,则有(1)当与独立时,与相容;(2)当与不相容时,与不独立。证明:(1)因为与独立,所以,与相容。(2)因为,而,,与不独立。7.已知事件相互独立,求证与也独立。证明:因为、、相互独立,与独立。8.甲、乙、丙三机床独立工作,在同一段时间内它们不需要工人照顾的概率分别为0.7,0.8和0.9,求在这段时间内,最多只有一台机床需要工人照顾的概率。
20解:令分别表示甲、乙、丙三机床不需要工人照顾,那么令表示最多有一台机床需要工人照顾,那么9.如果构成系统的每个元件能正常工作的概率为,(称为元件的可靠性),假设各元件能否正常工作是相互独立的,计算下面各系统的可靠性。系统I12nn+1n+22n系统II1n+12n+2n2n注:利用第7题的方法可以证明与时独立。解:令“系统(Ⅰ)正常工作”“系统(Ⅱ)正常工作”“第个元件正常工作”,相互独立。那么10.10张奖券中含有4张中奖的奖券,每人购买1张,求
20(1)前三人中恰有一人中奖的概率;(2)第二人中奖的概率。解:令“第个人中奖”,(1)或(2)11.在肝癌诊断中,有一种甲胎蛋白法,用这种方法能够检查出95%的真实患者,但也有可能将10%的人误诊。根据以往的记录,每10000人中有4人患有肝癌,试求:(1)某人经此检验法诊断患有肝癌的概率;(2)已知某人经此检验法检验患有肝癌,而他确实是肝癌患者的概率。解:令“被检验者患有肝癌”,“用该检验法诊断被检验者患有肝癌”那么,(1)(2)12.一大批产品的优质品率为30%,每次任取1件,连续抽取5次,计算下列事件的概率:(1)取到的5件产品中恰有2件是优质品;(2)在取到的5件产品中已发现有1件是优质品,这5件中恰有2件是优质品。解:令“5件中有件优质品”,(1)
20(2)13.每箱产品有10件,其次品数从0到2是等可能的。开箱检验时,从中任取1件,如果检验是次品,则认为该箱产品不合格而拒收。假设由于检验有误,1件正品被误检是次品的概率是2%,1件次品被误判是正品的概率是5%,试计算:(1)抽取的1件产品为正品的概率;(2)该箱产品通过验收的概率。解:令“抽取一件产品为正品”“箱中有件次品”,“该箱产品通过验收”(1)(2)14.假设一厂家生产的仪器,以概率0.70可以直接出厂,以概率0.30需进一步调试,经调试后以概率0.80可以出厂,并以概率0.20定为不合格品不能出厂。现该厂新生产了台仪器(假设各台仪器的生产过程相互独立),求:(1)全部能出厂的概率;(2)其中恰有2件不能出厂的概率;(3)其中至少有2件不能出厂的概率。解:令“仪器需进一步调试”;“仪器能出厂”“仪器能直接出厂”;“仪器经调试后能出厂”显然,那么所以令“件中恰有件仪器能出厂”,(1)(2)(3)15.进行一系列独立试验,每次试验成功的概率均为,试求以下事件的概率:
20(1)直到第次才成功;(2)第次成功之前恰失败次;(3)在次中取得次成功;(4)直到第次才取得次成功。解:(1)(2)(3)(4)16.对飞机进行3次独立射击,第一次射击命中率为0.4,第二次为0.5,第三次为0.7.击中飞机一次而飞机被击落的概率为0.2,击中飞机二次而飞机被击落的概率为0.6,若被击中三次,则飞机必被击落。求射击三次飞机未被击落的概率。解:令“恰有次击中飞机”,“飞机被击落”显然:而,,,所以;
20习题1.3解答1.设为随机变量,且(),则(1)判断上面的式子是否为的概率分布;(2)若是,试求和.解:令(1)显然,且所以为一概率分布。(2)为偶数2.设随机变量X的概率分布为(),且,求常数.解:,而,即3.设一次试验成功的概率为,不断进行重复试验,直到首次成功为止。用随机变量表示试验的次数,求的概率分布。解:4.设自动生产线在调整以后出现废品的概率为p=0.1,当生产过程中出现废品时立即进行调整,X代表在两次调整之间生产的合格品数,试求(1)的概率分布;(2)。解:(1)(2)
205.一张考卷上有5道选择题,每道题列出4个可能答案,其中有1个答案是正确的。求某学生靠猜测能答对至少4道题的概率是多少?解:因为学生靠猜测答对每道题的概率为,所以这是一个,的独立重复试验。6.为了保证设备正常工作,需要配备适当数量的维修人员。根据经验每台设备发生故障的概率为0.01,各台设备工作情况相互独立。(1)若由1人负责维修20台设备,求设备发生故障后不能及时维修的概率;(2)设有设备100台,1台发生故障由1人处理,问至少需配备多少维修人员,才能保证设备发生故障而不能及时维修的概率不超过0.01?解:(1)(按(泊松)分布近似)(2)(按(泊松)分布近似)查表得7.设随机变量服从参数为的Poisson(泊松)分布,且,求(1);(2).解:8.设书籍上每页的印刷错误的个数X服从Poisson(泊松)分布。经统计发现在某本书上,有一个印刷错误与有两个印刷错误的页数相同,求任意检验4页,每页上都没有印刷错误的概率。解:,即9.在长度为的时间间隔内,某急救中心收到紧急呼救的次数服从参数为的Poisson分布,而与时间间隔的起点无关(时间以小时计),求(1)某一天从中午12时至下午3时没有收到紧急呼救的概率;(2)某一天从中午12时至下午5时收到1次紧急呼救的概率;9.在长度为t的时间间隔内,某急救中心收到紧急呼救的次数X服从参数为的Poisson(泊松)分布,而与时间间隔的起点无关(时间以小时计).求(1)某一天从中午12时至下午3时没有收到紧急呼救的概率;(2)某一天从中午12时至下午5时收到1次紧急呼救的概率;
20解:(1)(2)10.已知的概率分布为:-2-101232a3aaa2a试求(1);(2)的概率分布。解:(1)。(2)11.设连续型随机变量的概率密度曲线如图1.3.8所示.f(x)图1.3.8xto1230.5试求:(1)的值;(2)的概率密度;(3).解:(1)
20(2)(3)12.设连续型随机变量的概率密度为试确定常数并求.解:令,即,即13.乘以什么常数将使变成概率密度函数?解:令即即14.随机变量,其概率密度函数为()试求;若已知,求.解:,
20若,由正态分布的对称性可知.15.设连续型随机变量的概率密度为以表示对的三次独立重复试验中“”出现的次数,试求概率.解:。16.设随机变量服从[1,5]上的均匀分布,试求.如果(1);(2).解:的概率密度为(1)(2)17.设顾客排队等待服务的时间(以分计)服从的指数分布。某顾客等待服务,若超过10分钟,他就离开。他一个月要去等待服务5次,以表示一个月内他未等到服务而离开的次数,试求的概率分布和.解:
20习题1.4解答1.已知随机变量的概率分布为,,,试求的分布函数;;画出的曲线。解:;曲线:2.设连续型随机变量的分布函数为试求:(1)的概率分布;(2).解:(1)(2)3.从家到学校的途中有3个交通岗,假设在各个交通岗遇到红灯的概率是相互独立的,且概率均是0.4,设为途中遇到红灯的次数,试求(1)的概率分布;(2)的分布函数。解:(1)列成表格
20(2)4.试求习题1.3中第11题的分布函数,并画出的曲线。解:5.设连续型随机变量的分布函数为试求:(1)的值;(2);(3)概率密度函数.解:(1)又
20(2)(3)6.设为连续型随机变量,其分布函数为试确定中的的值。解:又又又即7.设随机变量的概率密度函数为,试确定的值并求和.解:即8.假设某地在任何长为(年)的时间间隔内发生地震的次数服从参数为的Poisson(泊松)分布,表示连续两次地震之间相隔的时间(单位:年),试求:(1)证明服从指数分布并求出的分布函数;(2)今后3年内再次发生地震的概率;(3)今后3年到5年内再次发生地震的概率。解:(1)当时,当时,
20服从指数分布()(2)(3)9.设,试计算(1);(2);(3);(4).解:(1)(2)(3)(4)10.某科统考成绩近似服从正态分布,第100名的成绩为60分,问第20名的成绩约为多少分?解:而又即,,11.设随机变量和均服从正态分布,,,而,,试证明.证明:
20.12.设随机变量服从[a,b]上的均匀分布,令,试求随机变量的密度函数。解:当时,当时,'
您可能关注的文档
- 生理学课件 第10章神经系统(全部专科)
- 生理学课件 第十章 神经系统III
- 生理学课件 呼吸(多媒体)2016
- GBT 33404-2016 白酒感官品评导则
- (2015年最新)苏教版六年级下册语文补充习题答案.doc
- (最新部分)传感器原理及工程应用郁有文版习题参考答案.doc
- (第三版)结构设计原理课后习题答案(1--9章).doc
- (第三章)《计算机基础实用教程》实验内容(习题含答案).doc
- (经典总结)中国政法大学海商法习题及答案.doc
- 02018江苏省自学考试数学教育学大纲解析及课后习题答案.doc
- 02323《操作系统概论》课后习题答案.pdf
- 03297 企业文化(2012年版)课后习题答案.pdf
- 03449港口物流管理思考题答案.doc
- 03708 中国近代史纲要试题及答案(全套).doc
- 0512号文件 机械工程测试技术基础第三版课后习题答案.pdf
- 05《会计学基础》课后习题参考答案.doc
- 06《工程测量》第六章 小地区控制测量作业与习题答案.pdf
- 06会计学基础练习答案.doc