- 766.00 KB
- 2022-04-29 14:04:28 发布
- 1、本文档共5页,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,可选择认领,认领后既往收益都归您。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细先通过免费阅读内容等途径辨别内容交易风险。如存在严重挂羊头卖狗肉之情形,可联系本站下载客服投诉处理。
- 文档侵权举报电话:19940600175。
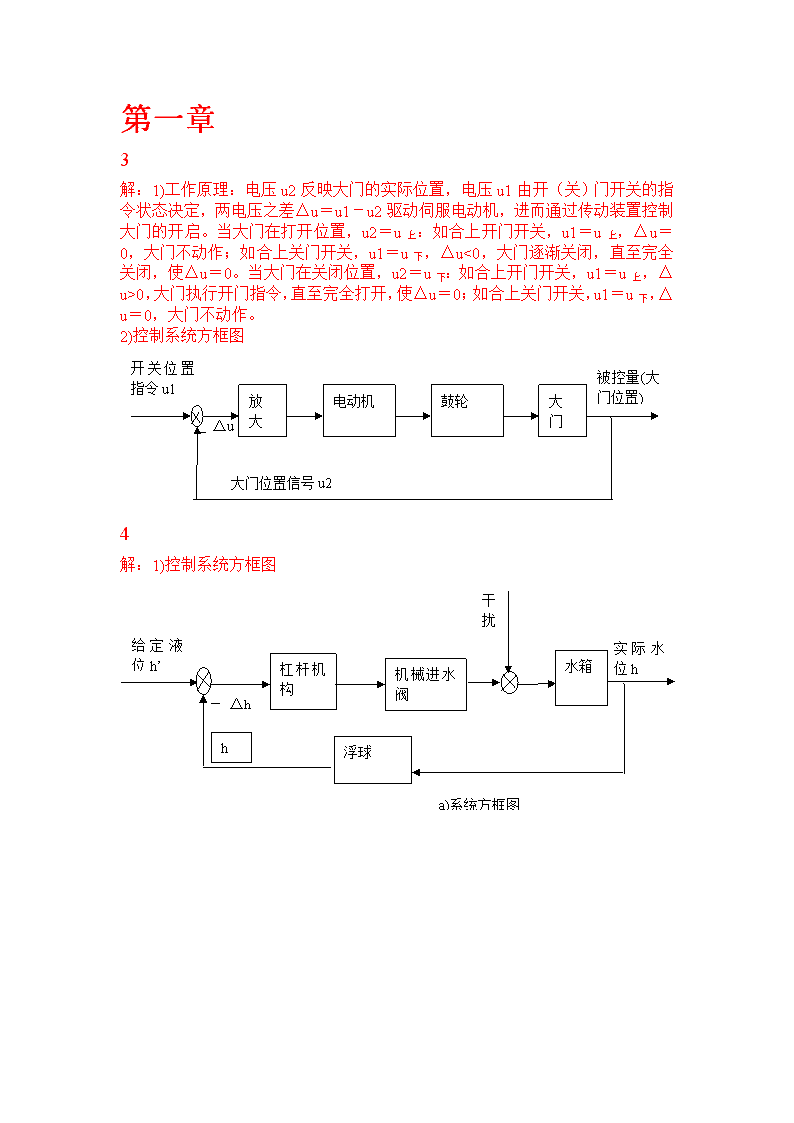
'第一章3解:1)工作原理:电压u2反映大门的实际位置,电压u1由开(关)门开关的指令状态决定,两电压之差△u=u1-u2驱动伺服电动机,进而通过传动装置控制大门的开启。当大门在打开位置,u2=u上:如合上开门开关,u1=u上,△u=0,大门不动作;如合上关门开关,u1=u下,△u<0,大门逐渐关闭,直至完全关闭,使△u=0。当大门在关闭位置,u2=u下:如合上开门开关,u1=u上,△u>0,大门执行开门指令,直至完全打开,使△u=0;如合上关门开关,u1=u下,△u=0,大门不动作。2)控制系统方框图_△u放大电动机鼓轮开关位置指令u1大门位置信号u2被控量(大门位置)大门4解:1)控制系统方框图-△h实际水位h杠杆机构机械进水阀水箱浮球给定液位h’h干扰a)系统方框图
-△h实际水位h电气开关电磁进水阀水箱浮球给定液位h’h干扰b)系统方框图2)工作原理:a)水箱是控制对象,水箱的水位是被控量,水位的给定值h’由浮球顶杆的长度给定,杠杆平衡时,进水阀位于某一开度,水位保持在给定值。当有扰动(水的使用流出量和给水压力的波动)时,水位发生降低(升高),浮球位置也随着降低(升高),通过杠杆机构是进水阀的开度增大(减小),进入水箱的水流量增加(减小),水位升高(降低),浮球也随之升高(降低),进水阀开度增大(减小)量减小,直至达到新的水位平衡。此为连续控制系统。b)水箱是控制对象,水箱的水位是被控量,水位的给定值h’由浮球拉杆的长度给定。杠杆平衡时,进水阀位于某一开度,水位保持在给定值。当有扰动(水的使用流出量和给水压力的波动)时,水位发生降低(升高),浮球位置也随着降低(升高),到一定程度后,在浮球拉杆的带动下,电磁阀开关被闭合(断开),进水阀门完全打开(关闭),开始进水(断水),水位升高(降低),浮球也随之升高(降低),直至达到给定的水位高度。随后水位进一步发生升高(降低),到一定程度后,电磁阀又发生一次打开(闭合)。此系统是离散控制系统。2-1解:(c)确定输入输出变量(u1,u2)得到:一阶微分方程(e)确定输入输出变量(u1,u2)
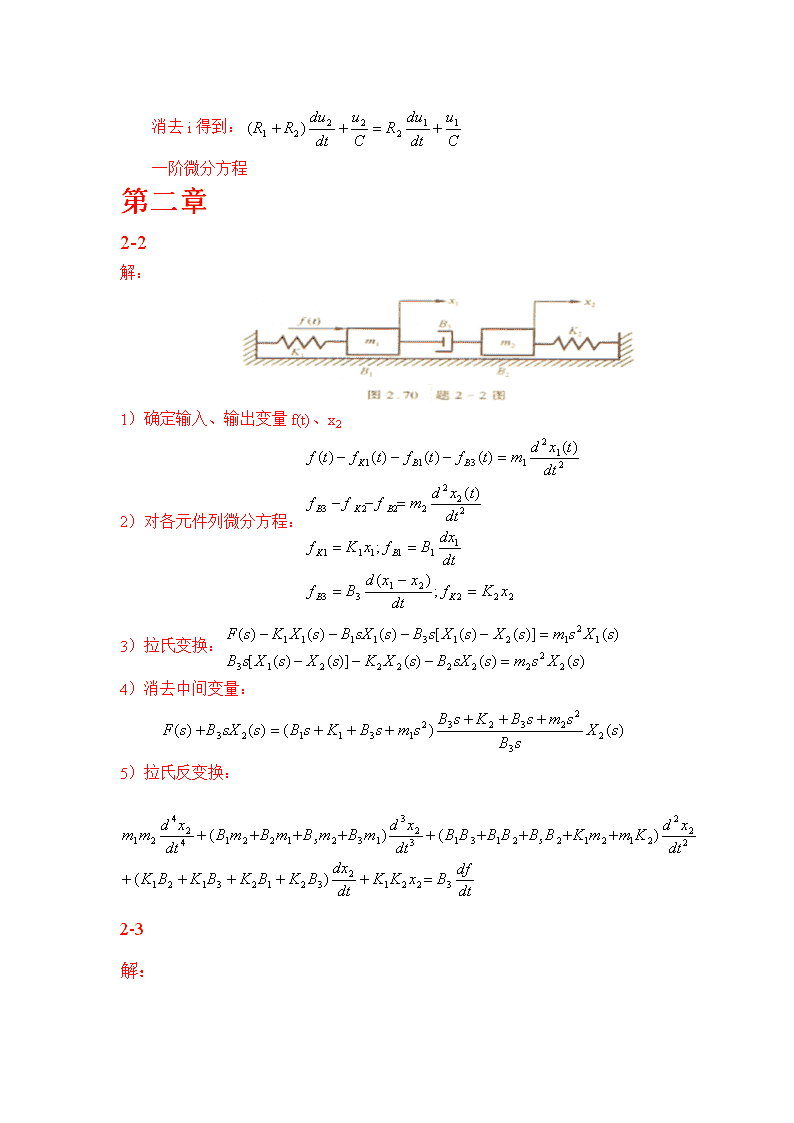
消去i得到:一阶微分方程第二章2-2解:1)确定输入、输出变量f(t)、x22)对各元件列微分方程:3)拉氏变换:4)消去中间变量:5)拉氏反变换:2-3解:
(2)(4)(5)(6)2-5解:1)D(s)=0,得到极点:0,0,-2,-5M(s)=0,得到零点:-1,,,2)D(s)=0,得到极点:-2,-1,-2M(s)=0,得到零点:0,0,-13)D(s)=0,得到极点:0,,M(s)=0,得到零点:-2,,4)D(s)=0,得到极点:-1,-2,M(s)=0,得到零点:2-8解:1)a)建立微分方程b)拉氏变换
c)画单元框图(略)d)画系统框图-Xo(s)--F(s)Fi(s)a/b1/ms2K1k21/Bs2)a)建立微分方程:b)拉氏变换:c)绘制单元方框图(略)4)绘制系统框图
+--X0(s)B1sK1/ms2B2sXi(s)2-11解:a)b)2-14解:(1)(2)由于扰动产生的输出为:要消除扰动对输出的影响,必须使得到:
得到:第三章3-1解:1)法一:一阶惯性环节的调整时间为4T,输出达稳态值的98%,故:4T=1min,得到:T=15s法二:求出一阶惯性环节的单位阶跃时间响应,代入,求出。2)法一:输入信号,是速度信号;法二:利用误差信号E(s)3-3解:部分分式展开:系数比较得到:A+B+C=011A+6B+5C=030A=13得到:A=13/30=0.433;B=-13/5=-2.6;C=13/6=2.1667拉氏反变换:3-4
解:闭环传递函数为:(1)单位阶跃函数的拉氏变换:部分分式展开:系数比较得到:4A+3B=0A-3C=0A=1得到:A=1,B=-4/3,C=1/3拉氏反变换:(2)法一、利用微分关系,把结果(1微分)法二、单位脉冲函数的拉氏变换:部分分式展开:系数比较得到:A+B=04A+B=4得到:A=4/3,B=-4/3拉氏反变换:3-6解:闭环传递函数为:得到:rad/s;相位移:
时间响应各参数:3-7解:1)求闭环传递函数二阶振动环节:得到:2)求结构参数最大超调量得到:峰值时间得到:3)求K,Kh代入1)得到:4)利用结构参数求其它时域指标调整时间
上升时间3-8解:闭环传递函数1)K=200:此时,系统为过阻尼系统,为两个惯性环节串联,无振荡动态参数。2)K=1500,得到:最大超调量峰值时间调整时间上升时间振动次数3)K=13.5,得到:此时,系统为过阻尼系统,为两个惯性环节串联,无振荡动态参数。4)对于二阶系统传递函数化为标准形式后,只要不变,系统调整时间ts不变;随着增大,过渡过程在缩短(tp,tr),但总过渡时间(调整时间ts)不变;而随着的减小,振动幅度在加剧,振动次数N、超调量Mp都在加大。3-8解:闭环传递函数
1)K=200:最大超调量峰值时间调整时间上升时间振动次数2)K=150,得到:依次得到的动态性能指标:0.54,0037s,0.175s,0.02s,2.34。3)K=13.5,得到:此时,系统为过阻尼系统,为两个惯性环节串联。4)对于二阶系统传递函数化为标准形式后,只要不变,系统调整时间ts不变;随着增大,过渡过程在缩短(tp,tr),但总过渡时间(调整时间ts)不变;而随着的减小,振动幅度在加剧,振动次数N、超调量Mp都在加大。3-9解:开环传递函数为:单位反馈系统的:H(s)=1位置稳态误差系数为:速度稳态误差系数为:加速度稳态误差系数为:
单位阶跃输入的稳态误差:单位速度输入的稳态误差:单位加速度输入的稳态误差:3-10解:开环传递函数,此系统为I型系统。稳态误差系数:1)单位阶跃输入稳态误差:2)单位速度输入稳态误差:3)单位加速度输入稳态误差;法二:3-11解:开环传递函数,此系统为I型系统。1)稳态误差系数2)输入信号为阶跃信号、速度信号和加速度信号的组合,它们的系数分别为:根据信号线性叠加的原理,系统的稳定误差为:
a)当时,b)当时,c)当时,3-12解:1)仅有输入信号作用下的稳态误差偏差传递函数误差信号稳态误差2)仅有干扰信号作用下的稳态误差干扰偏差传递函数干扰误差信号干扰稳态误差3)系统总稳态误差:3-13解:特征根分别为:-8,-9,-4+j5,-4-j5。闭环系统的所有特征根均具有负实部,所以系统是稳定的。3-14
解:单位反馈系统的闭环传递函数:特征根为:要使系统稳定,上述特征根的实部必须为负实部:当时,可保证特征根具有负实部。解得:因K、T均大于零,所以上式成立。所以系统是稳定的。3-15(1)解:法一:劳思阵列第一列有负数,系统不稳定。法二:a0=1,a1=0,a2=-15,a3=126;三阶系统,因所有系数不全为正,所以不稳定。(2)解:劳斯阵列劳思阵列中第一列元素的符号全为正,系统是稳定的。(3):法一:劳思阵列
劳思阵列中第一列元素的符号全为正,系统是稳定的。法二:a0=1,a1=4,a2=5,a3=10;因为三阶系统,a0,a1,a2,a3均大于0,且a1×a2=20>a0×a3=10,所以该三阶系统稳定。(5):法一:劳思阵列:辅助多项式:劳思阵列第一列中无负号,但有一列的元素全为0,所以系统是临界稳定的。法二:a0=1,a1=10,a2=16,a3=160;因为三阶系统,a0,a1,a2,a3均大于0,且a1×a2=160=a0×a3=160,所以该三阶系统临界稳定。3-16(2)解:劳思阵列系统稳定的条件,劳思阵列第一列元素全为正号,即:由式1)得:k>0式2)得:k>10/99式3)得:k<99/10K的取值无法同时满足上述三个条件,所以劳思阵列第一列中一定有负号,所以系统是不稳定的。
(4)解:劳思阵列系统稳定的条件,劳思阵列第一列元素全为正号,即:由式1)、2)得:k>1式3)可化为:显然,上式无法满足,即:无论k取何值,式1)、2)、3)条件都无法同时满足,所以劳思阵列第一列中一定有负号,所以系统是不稳定的。第四章4-4解:闭环传递函数频率特性幅频特性相频特性1),稳态输出2)
稳态输出3)稳态输出4-9解:1);2)、;4-121)解a)典型环节:放大环节:2惯性环节1:转折频率惯性环节2:转折频率b)在博德图上标出w1,w2c)对数幅频特性:d)低频渐近线(w1/T3后系统增益增加,校正后的幅频特性曲线上移,穿越斜率右-40dB/dec变为-20dB/dec,提高了穿越频率wc,系统响应的快速性增加;相位超前,系统的相位裕量也增加,提高了系统的稳定性;但对抗高频干扰的能力下降。5-6解:(1)确定开环增益:Kv=K≥7,取K=7开环频率特性对数幅频特性相频特性并画出未校正开环系统的博德图。(2)计算未校正系统的幅值穿越频率和相位裕量令L(wc)=0,得到
得到幅值穿越频率为:相位裕量为:不能满足性能要求,考虑到系统对稳态精度有要求,而对响应快速性没具体要求,所以可选用滞后校正装置。(3)确定校正后的幅值穿越频率取则:得到校正后的幅值穿越频率为:(4)确定滞后校正装置的参数滞后校正装置的频率特性滞后校正装置在新幅值穿越频率处提供的幅值增益分贝:所以:得到:为使校正装置的增大滞后相角远离校正后的幅值穿越频率,可选校正装置的一个转折频率为:得到T2=4.35校正装置的传递函数为:(5)验算校正后的幅值裕量和相位裕量校正后的开环传递函数求相位裕量:
求幅值裕量:解得:满足设计要求。'
您可能关注的文档
- 《成本会计习题集》1-13章答案.doc
- 《成本会计学》(于富生)课后习题答案.doc
- 《成本会计学》习题集及答案.doc
- 《成本会计学》人大第五版课后习题答案.doc
- 《房屋建筑学》复习题及答案.doc
- 《技术经济学》课后解答(高教版).doc
- 《投资学》课后习题参考答案.doc
- 《投资学》课后习题参考答案.pdf
- 《指数函数和对数函数》练习与习题参考解答.doc
- 《控制工程基础》第四章习题解题过程和参考答案.doc
- 《控制电机》课后习题答案.pdf
- 《操作系统原理》习题及参考答案.pdf
- 《操作系统实用教程》课后题参考答案.doc
- 《操作系统教程》习题答案.doc
- 《政治生活》第1单元复习题及答案.doc
- 《教育心理学(皮连生)》课后习题答案.doc
- 《教育技术》课后习题答案参考(北师大).doc
- 《数值分析》黄仿伦改编英文版课后习题答案.pdf