- 870.00 KB
- 2022-04-29 14:08:00 发布
- 1、本文档共5页,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,可选择认领,认领后既往收益都归您。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细先通过免费阅读内容等途径辨别内容交易风险。如存在严重挂羊头卖狗肉之情形,可联系本站下载客服投诉处理。
- 文档侵权举报电话:19940600175。
'《电力拖动自动控制系统—运动控制系统》习题2-2调速系统的调速范围是1000~100r/min,要求静差率s=2%,那么系统允许的稳态速降是多少?解:系统允许的稳态速降∆nN=snmin(1−s)=0.02×100(1−0.02)=2.04(rmin)2-5某龙门刨床工作台采用晶闸管整流器-电动机调速系统。已知直流电动机PN=60kW,UN=220V,IN=305A,nN=1000rmin,主电路总电阻R=0.18Ω,Ce=0.2V•minr,求:(1)当电流连续时,在额定负载下的转速降落∆nN为多少?(2)开环系统机械特性连续段在额定转速时的静差率sN多少?(3)额定负载下的转速降落∆nN为多少,才能满足D=20,s≤5%的要求。解:(1)当电流连续时,在额定负载下的转速降落∆nN=INR=305×0.18=274.5(rmin)Ce0.2(2)开环系统机械特性连续段在额定转速时的静差率nsN=N∆nN+∆nN=274.5≈0.215=21.5%1000+274.5(3)额定负载下满足D=20,s≤5%要求的转速降落∆nN=nNsD(1−s)=1000×0.0520×(1−0.05)≈2.63(rmin)
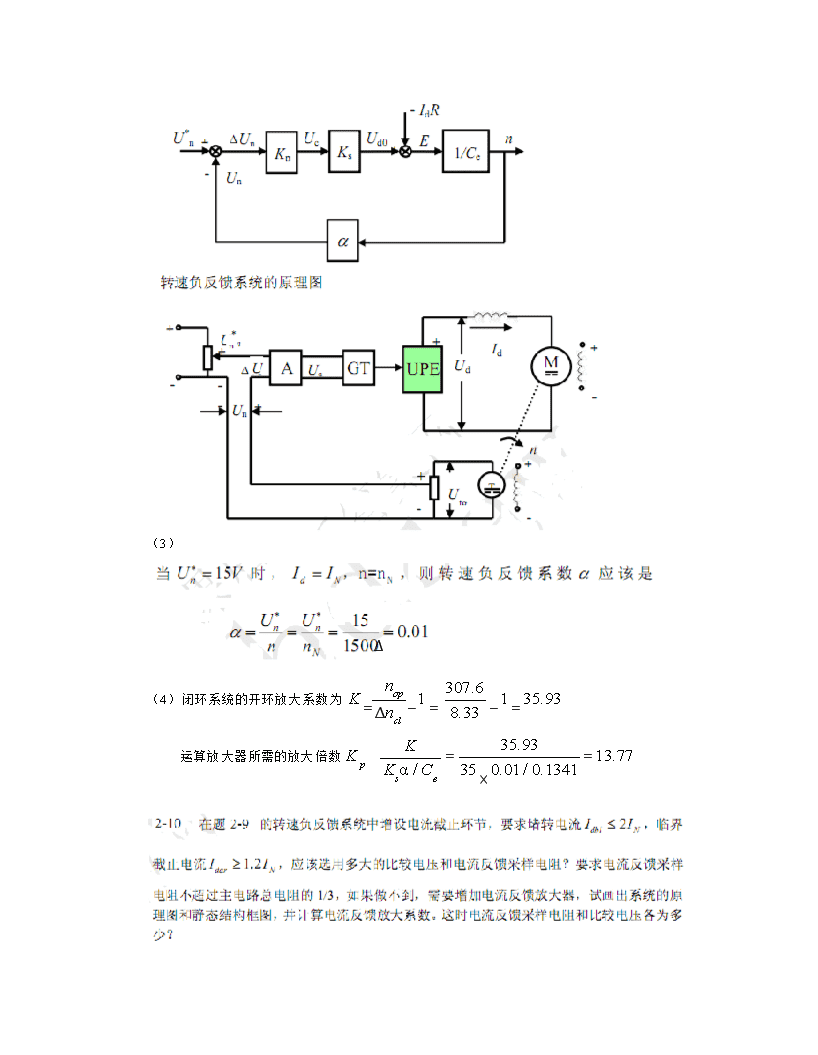
UN解:(1)Ce=−IdRanN=220−12.5×1.5=0.1341V⋅min/r1500∆nop=RINCe=12.5×(1.5+1.0+0.8)0.1341=307.6r/min(2)∆n=nNs≤1500×0.1=8.33r/minclD(1−s)20×(1−0.1)
(3)∆nop307.6(4)闭环系统的开环放大系数为K=−1=−1=35.93∆nclK8.3335.93运算放大器所需的放大倍数Kp=Ksα/Ce==13.7735×0.01/0.1341
解:R=4.8ΩRs/R=0.3125<1/3图见49页2-12有一晶闸管-电动机调速系统,已知:电动机PN=2.8kW,UN=220V,IN=15.6A,nN=1500rmin,Ra=1.5Ω,整流装置内阻Rrec=1Ω,电枢回路电抗器电阻RL=0.8Ω,触发整流环节的放大倍数Ks=35。求:(1)系统开环时,试计算调速范围D=30时的静差率s。
(2)当D=30,s=10%时,计算系统允许的稳态速降。ndN(3)如组成转速负反馈有静差调速系统,要求D=30,s=10%,在U*=10V时I=I,n=nN,计算转速反馈系数α和放大器放大系数Kp。解:先计算电动机的反电动势系数Ce=UN−INRanN=220−15.6×1.5=0.131(V•minr)1500系统开环时的额定转速降落IN(Ra+Rrec+RL)15.6×(1.5+1+0.8)C∆nNop=e=≈393(rmin)0.131(1)系统开环时,调速范围D=30时的静差率s=D∆nNnN+D∆nN=30×3931500+30×393≈0.887=88.7%;(2)当D=30,s=10%时,系统允许的稳态速降∆nN=nNsD(1−s)=1500×0.130×(1−0.1)≈5.56(rmin)(3)如组成转速负反馈有静差调速系统,要求D=30,s=10%,则系统开环放大系数∆nopK=−1=∆ncl393−1≈69.68;5.56α=n转速反馈系数U*nN=101500≈0.0067(V•minr)放大器放大系数Kp=KCeKsα=69.68×0.131≈38.93。35×0.0067Ci=Ri/τi=14µF
4h=3σ%=2(∆Cmax%)(λ−z)∆nNnCn*T∑n=63.4%Tbm5-1一台三相鼠笼异步电动机的铭牌数据为:额定电压UN=380V,额定转速nN=960rmin,额定频率fN=50Hz,定子绕组为Y联接。由实验测得定子电阻Rs=0.35Ω,定子漏感Lls=0.006H,定子绕组产生气隙主磁通的等效电感Lm=0.26H,转子电阻Rr′=0.5Ω,转子漏感Ll′r=0.007H,转子参数已折算到定子侧,忽略铁芯损耗。(1)画出异步电动机T形等效电路和简化电路。(2)额定运行时的转差率sN,定子额定电流I1N和额定电磁转矩。(3)定子电压和频率均为额定值时,理想空载时的励磁电流I0。(4)定子电压和频率均为额定值时,临界转差率sm和临界转矩Tem,画出异步电动机的机械特性。解:(1)异步电动机T形等效电路
异步电动机简化电路(2)由于额定转速nN=960rmin,同步转速n1=60fNnp=60×50=1000(r3min),额定运行时的转差率sN=n1−nn1=1000−9601000=0.04由异步电动机T形等效电路,C1=1+Rs+jω1LlsjωL=1+LlsL−jRs2πfL=1+0.0060.260.35−j≈1.023−j0.004≈1.023100π×0.261mmNm可得转子相电流幅值
Ir′=⎛+CRr′Us2+ω2(L+CL′)2⎞⎜R⎟⎜s1s⎟1ls1lr⎝N⎠=⎛⎜0.35+1.023×⎝=22020.5⎞⎟0.04⎠220+(100π)2×(0.006+1.023×0.007)2172.5939+17.0953=15.9735(A)气隙磁通在定子每相绕组中的感应电动势2⎜r⎟E=I′⎛R′⎞+ω2L′2=15.9735×156.25+4.8361≈202.7352(V)sgr1lr⎝N⎠额定运行时的励磁电流幅值I=Eg0ωL=202.7352≈2.482(A)100π×0.261m由异步电动机简化电路,额定运行时的定子额定电流幅值I1N=Us⎛+=R2′⎞+ω2(L=⎜+L′)2⎛0.35+0.5⎞220+(100π)2×(0.006+0.007)2⎝⎟2=⎝2s2⎠020.04⎠1⎜Rs.1225+⎟16.619lslr6576=16.316(4A)额定电磁转矩T=Pm3nR′3×30.5r=pI′2r=×15.97352×≈91.37(N⋅m)(依据T形等效电路)ωmω1sNe或100π0.04Pm3np2Rr′3×320.5Te==ωωI1Ns=×16.3164×≈95.33(N⋅m)(依据简化等效电路)m1N100π0.04(3)定子电压和频率均为额定值时,理想空载时的励磁电流I0=UsR2+ω2(L=+L)22200.352+(100π)2×(0.006+0.26)2=2.633(A)s1lsm(4)定子电压和频率均为额定值时,临界转差率sm=Rr′R2+ω2(L=+L′)20.50.352+(100π)2×(0.006+0.007)2=0.122s临界转矩Tem=1lslr3nU23×3×2202ps=2⎡RR22(LL)2⎤200×π×[0.35+0.352+(100π)2×(0.006+0.007)2]
=15ω51.83(sN+⋅m)s+ω1ls+l′r异步电动机的机械特性:
n1Sn0Sm10TemTe5-6异步电动机参数如习题5-1所示,输出频率f等于额定频率fN时,输出电压U等于额定电压UN,考虑低频补偿,若频率f=0,输出电压U=10%UN。(1)求出基频以下电压频率特性曲线U=f(f)的表达式,并画出特性曲线。(2)当f=5Hz和f=2Hz时,比较补偿与不补偿的机械特性曲线,两种情况下的临界转矩Temax。解:(1)UN=220(A)斜率
k=UN−0.1UNfN−0=220−22=3.96,50−0考虑低频补偿时,电压频率特性曲线U=3.96f+22;不补偿时,电压频率特性曲线(2)当f=5Hz时U=220f50=4.4fA、不补偿时,输出电压U=4.4fps3nU2T=em=22(V),临界转矩=3×3×2222⎡RR22(LL)2⎤20×π×[0.35+0.352+(10π)2×(0.006+0.007)2]=78ω.0184(sN+⋅m)s+ω1ls+l′rB、补偿时,输出电压U=3.96f+22=41.8(V)ps3nU23×3×41.82Tem=2⎡RR22(LL)2⎤=20×π×[0.35+0.352+(10π)2×(0.006+0.007)2]=28ω11.88s3(+N⋅ms)+ω1ls+l′r当f=2Hz时A、不补偿时,输出电压U=4.4fps3nU2T=em=8.8(V),临界转矩=3×3×8.822⎡RR22(LL)2⎤8×π×[0.35+0.352+(4π)2×(0.006+0.007)2]=37ω.6166(sN+⋅m)s+ω1ls+l′rB、补偿时,输出电压U=3.96f+22=29.92(V)ps3nU23×3×29.922Tem=2⎡RR22(LL)2⎤=8×π×[0.35+0.352+(4π)2×(0.006+0.007)2]ω1s+s+ω1ls+l′r5-8=两4电35平.41P9W(NM⋅m逆)变器主回路,采用双极性调制时,用“1“表示上桥臂开通,”0“表示上桥臂关断,共有几种开关状态,写出其开关函数。根据开关状态写出其电压矢量表达式,画出空间电压矢量图。解:
6-1按磁动势等效、功率相等原则,三相坐标系变换到两相静止坐标系的变换矩阵为C32=⎡12⎢1−2⎢−1⎤2⎥⎥3⎢03−=3⎥22⎥⎦现有三相正弦对称电流i=Isin(ωt)、i=Isin(ωt−2π)、i=Isin(ωt+2π),求AmBm3Cm3变换后两相静止坐标系中的电流isα和isβ,分析两相电流的基本特征与三相电流的关系。1⎡−1−⎡1⎤⎢⎤Imsin(ωt)⎥⎡isα⎤2⎢解:=22⎥⎢Isin(ωt−2π)⎥=3⎡Imsin(ωt)⎤;⎢⎥⎢⎥⎢m⎥⎢⎥⎣isβ⎦3⎢03−=3⎥⎢3⎥2⎣−Imcos(ωt)⎦22⎢Isin(ωt+2π)⎥m36-2两相静止坐标系到两相旋转坐标系的变换矩阵为⎡cosϕC2s2r=⎢⎣−sinϕsinϕ⎤⎦cosϕ⎥将习题6-1中的静止坐标系中的电流isα和isβ变换到两相旋转坐标系中的电流isd和isq,坐dϕ标系旋转速度为dt=ω1。分析当ω1=ω时,电流isd和isq的基本特征,电流矢量幅值=i+ii2sqssd2与三相电流幅值I的关系,其中ω是三相电源角频率。ω1>ω和ω1<ω时,misd和isq的表现形式。⎡isd⎤⎡cosϕsinϕ⎤3⎡Imsin(ωt)⎤3⎡Imsin(ωt−ϕ)⎤解:⎢⎥=⎢⎥⎢⎥=⎢⎥⎣isq⎦⎣−sinϕcosϕ⎦dϕ2⎣−Imcos(ωt)⎦2⎣−Imcos(ωt−ϕ)⎦由坐标系旋转速度为dt=ω1,则ϕ=ω1t+ϕ0(ϕ0为初始角位置)(1)当ω1=ω时,ϕ=ω1t=ωt+ϕ0,则isd=−isq=−
3Imsinϕ0,23Imcosϕ0,2223
is=isd+isq=Im;2(2)当ω1>ω和ω1<ω时,设ωs=ω1−ω,ωt−ϕ=−ωst−ϕ0,则⎡isd⎤3⎡Imsin(ωt−ϕ)⎤3⎡−Imsin(ωst+ϕ0)⎤⎢⎥=⎢⎥=⎢⎥。⎣isq⎦2⎣−Imcos(ωt−ϕ)⎦2⎣−Imcos(ωst+ϕ0)⎦'
您可能关注的文档
- 《现代经济学应用》练习题及答案(2013).doc
- 《现代通信原理》曹志刚清华大学出版社课后答案word版.doc
- 《生产与运营管理》练习题与参考答案.doc
- 《生产物流》复习题及答案.pdf
- 《生物化学》课后习题详细解答.doc
- 学简明教程》第四版_张丽萍_杨建雄_课后习题答案.doc
- 《用电监察员》中级工理论复习题及答案_2.doc
- 《用电监察员》中级工理论复习题合卷(含答案).doc
- 《田间试验与统计分析》第二版(明道绪 主编) 课后习题解答及复习资料 科学出版社.doc
- 《电力电子及技术》第五版部分习题答案.pdf
- 《电力电子技术(第二版)》课后习题及解答.doc
- 《电力电子技术》(第一二章)习题答案.doc
- 《电力电子技术》习题答案 王兆安.doc
- 《电力电子技术》习题答案(第四版).doc
- 《电力电子技术》习题答案(第四版,第五版,王兆安,王俊主编).doc
- 《电力电子技术》第四版课后习题答案.doc
- 《电力电子技术释疑与习题解析》4.3 习题提示与答案.pdf
- 《电力系统分析》综合练习题答案.doc