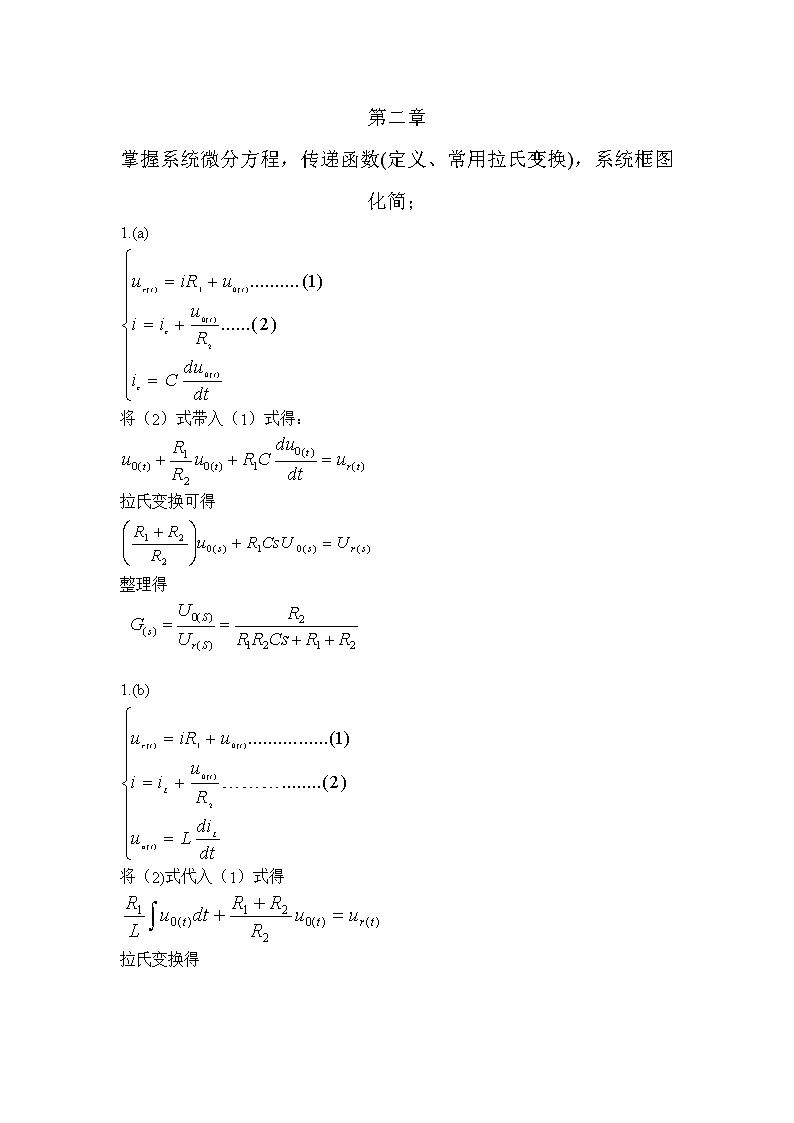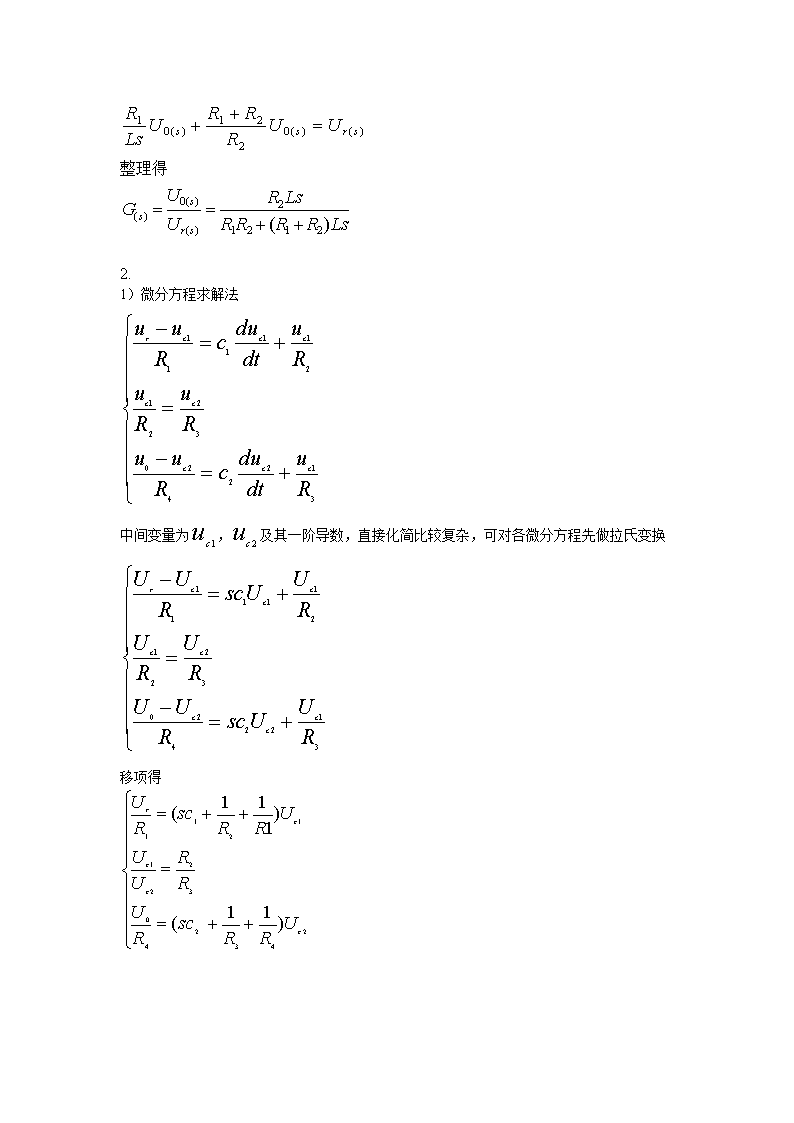- 1.17 MB
- 2022-04-29 14:10:01 发布
- 1、本文档共5页,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,可选择认领,认领后既往收益都归您。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细先通过免费阅读内容等途径辨别内容交易风险。如存在严重挂羊头卖狗肉之情形,可联系本站下载客服投诉处理。
- 文档侵权举报电话:19940600175。
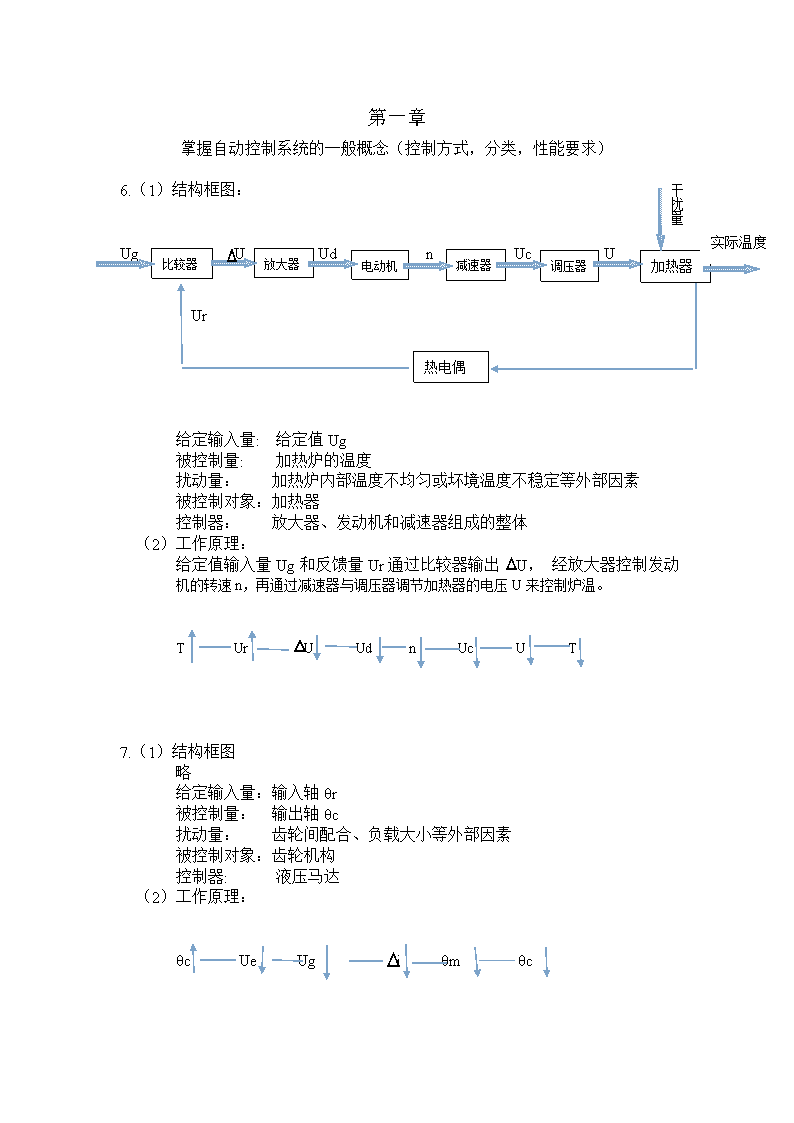
'第一章干扰量掌握自动控制系统的一般概念(控制方式,分类,性能要求)6.(1)结构框图:实际温度减速器调压器加热器电动机放大器比较器UgUUdnUcUUr热电偶给定输入量:给定值Ug被控制量:加热炉的温度扰动量:加热炉内部温度不均匀或坏境温度不稳定等外部因素被控制对象:加热器控制器:放大器、发动机和减速器组成的整体(2)工作原理:给定值输入量Ug和反馈量Ur通过比较器输出U,经放大器控制发动机的转速n,再通过减速器与调压器调节加热器的电压U来控制炉温。TUrUUdnUcUT7.(1)结构框图略给定输入量:输入轴θr被控制量:输出轴θc扰动量:齿轮间配合、负载大小等外部因素被控制对象:齿轮机构控制器:液压马达(2)工作原理:θcUeUgiθmθc
第二章掌握系统微分方程,传递函数(定义、常用拉氏变换),系统框图化简;1.(a)将(2)式带入(1)式得:拉氏变换可得整理得1.(b)将(2)式代入(1)式得拉氏变换得
整理得2.1)微分方程求解法中间变量为,及其一阶导数,直接化简比较复杂,可对各微分方程先做拉氏变换移项得
可得2)复阻抗法解得:3.分别以m2,m1为研究对象(不考虑重力作用)中间变量含一阶、二阶导数很难直接化简,故分别做拉氏变换消除Y1中间变量
10.系统框图化简:
11.系统框图化简:
第三章掌握时域性能指标,劳斯判据,掌握常用拉氏变换-反变换求解时域响应,误差等2.(1)求系统的单位脉冲响应2.(2)求系统的单位阶跃响应,和单位斜坡响应
9.解:由图可知该系统的闭环传递函数为又因为:联立1、2、3、4得所以
10.解:由题可知系统闭环传递函数为当k=10时,=10rad/s;=0.5;所以有当k=20时,=14.14rad/s;=0.35;所以有当02.5时,系统为欠阻尼,超调量%随着K增大而增大,和峰值时间随着K增大而减小;其中调整时间不随k值增大而变化;
14.(1)解,由题可知系统的闭环传递函数为
14.(2)解,由题可知系统的闭环传递函数为20.解:由题可知系统的开环传递函数为当输入为单位阶跃信号时,系统误差的拉氏变换为
25.解:由题可知系统的开环传递函数为当输入为给定单位阶跃信号时,系统在给定信号下误差的拉氏变换为当输入为扰动信号时,系统扰动信号下误差的拉氏变换为
第四章根轨迹法掌握轨迹的概念、绘制方法,以及分析控制系统4-2(2)G(s)=;解:分析题意知:由s(0.2s+1)(0.5s+1)=0得开环极点s1=0,s2=-2,s3=-5。(1)根轨迹的分支数等于3。(2)三条根轨迹的起点分别是实轴上的(0,j0),(-2,j0),(-5,j0),终止点都是无穷远处。(3)根轨迹在实轴上的轨迹段:[-2,0]段和[-∞,-5]段。(4)根轨迹的渐近线:由n=3,m=0渐近线与实轴的交点(5)根轨迹与实轴的分离点:A(s)=s(0.2s+1)(0.5s+1)B(s)=1由解得:s1=s2=(舍去)根轨迹如图所示σjw
(3)G(s)=解:分析题意知:由s(s+2)(s+3)=0得开环极点s1=0,s2=-2,s3=-3。由k(s+2)=0得开环零点为s=-2。(1)根轨迹的分支数等于3。(2)三条根轨迹的起点分别是实轴上的(0,j0),(-2,j0),(-5,j0),终止是(-2,j0)和无穷远处。(3)根轨迹在实轴上的轨迹段:[-3,0]段。(4)根轨迹的渐近线:由n=3,m=1渐近线与实轴的交点(5)根轨迹与实轴的分离点:A(s)=s(s+2)(s+3)B(s)=k(s+2)由解得:s1=s2=-2(舍去)s3=其中s1=s2=-2s是因为闭环特征方程的根恒有一根s=-2分离点取s=根轨迹如图所示σjw
4-3G(s)H(s)=;解:分析题意知:由s2(s+2)(s+5)=0得开环极点s1=s2=0,s3=-2,s4=-5。(1)根轨迹的分支数等于4。(2)三条根轨迹的起点分别是实轴上的(0,j0),(-2,j0),(-5,j0),终止点都是无穷远处。(3)根轨迹在实轴上的轨迹段:[-5,-2]段。(4)根轨迹的渐近线:由n=4m=0渐近线与实轴的交点(5)根轨迹与实轴的分离点:A(s)=s2(s+2)(s+5)B(s)=1由解得:s1=s2=-4s3=(舍去)根轨迹如图所示σjw
4-4(2)G(s)=;解:分析题意知:由s(0.1s+1)(s+1)=0得开环极点s1=0,s2=-1,s3=-10。(1)根轨迹的分支数等于3。(2)三条根轨迹的起点分别是实轴上的(0,j0),(-1,j0),(-10,j0),终止点都是无穷远处。(3)根轨迹在实轴上的轨迹段:[-1,0]段和[-∞,-10]段。(4)根轨迹的渐近线:由n=3,m=0渐近线与实轴的交点(5)根轨迹与实轴的分离点:A(s)=s(0.1s+1)(s+1)B(s)=1由解得:s1=0.49s2(舍去)根轨迹如图所示σjw闭环特征方程:s(0.1s+1)(s+1)+K=0将s=jw代入得10w-w3=0(1)-11w2+10K=0(2)解得K=11K>11时系统不稳定
4-6G(s)=;解:分析题意知:由s(s+3)(s+7)=0得开环极点s1=0,s2=-3,s3=-7。(1)根轨迹的分支数等于3。(2)三条根轨迹的起点分别是实轴上的(0,j0),(-3,j0),(-7,j0),终止点都是无穷远处。(3)根轨迹在实轴上的轨迹段:[-3,0]段和[-∞,-7]段。(4)根轨迹的渐近线:由n=3,m=0渐近线与实轴的交点(5)根轨迹与实轴的分离点:A(s)=s(s+3)(s+7)B(s)=1由解得:s1=-1.3s2=-5.4(舍去)根轨迹如图所示σjw闭环特征方程:s(s+3)(s+7)+k=0将s=jw代入得21w-w3=0(1)k=10w2(2)得k=210k210系统稳定再将s=-1.3代入闭环特征方程得k=12.612.6
您可能关注的文档
- 《编译原理实践及应用》习题的参考答案.doc
- 《网络协议分析 寇晓 机械工程出版社课后习题答案.pdf
- 《自动控制原理(第2版)》李晓秀(习题参考答案).doc
- 《自动控制原理》(李晓秀)习题参考答案 (修复的).docx
- 《自动控制原理》(李晓秀)习题参考答案-改.doc
- 《自动控制原理》(李晓秀)习题参考答案.doc
- 《自动控制原理》5章课后习题参考答案.doc
- 《自动控制原理》习题及解答.doc
- 《自动控制原理》清华大学出版社、北京交通大学出版社;姚佩阳主编,曹锦、常永昌等副主编,课后习题详解.doc
- 《自动控制原理》黄坚课后习题答案.doc
- 《自动控制原理答案》李明富 课后习题答案 人民邮电出版社.doc
- 《自动检测技术》第二版 王化祥 课后答案.pdf
- 《自然之道》课后巩固练习.doc
- 《自然地理学》课后思考题的一些答案.doc
- 《自考英语》(上册)课后习题答案.doc
- 《致电离辐射探测学》练习题.docx
- 《航海学》习题答案及解析.docx
- 《药物分析》习题答案.doc