- 1.87 MB
- 2022-04-29 14:08:11 发布
- 1、本文档共5页,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,可选择认领,认领后既往收益都归您。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细先通过免费阅读内容等途径辨别内容交易风险。如存在严重挂羊头卖狗肉之情形,可联系本站下载客服投诉处理。
- 文档侵权举报电话:19940600175。
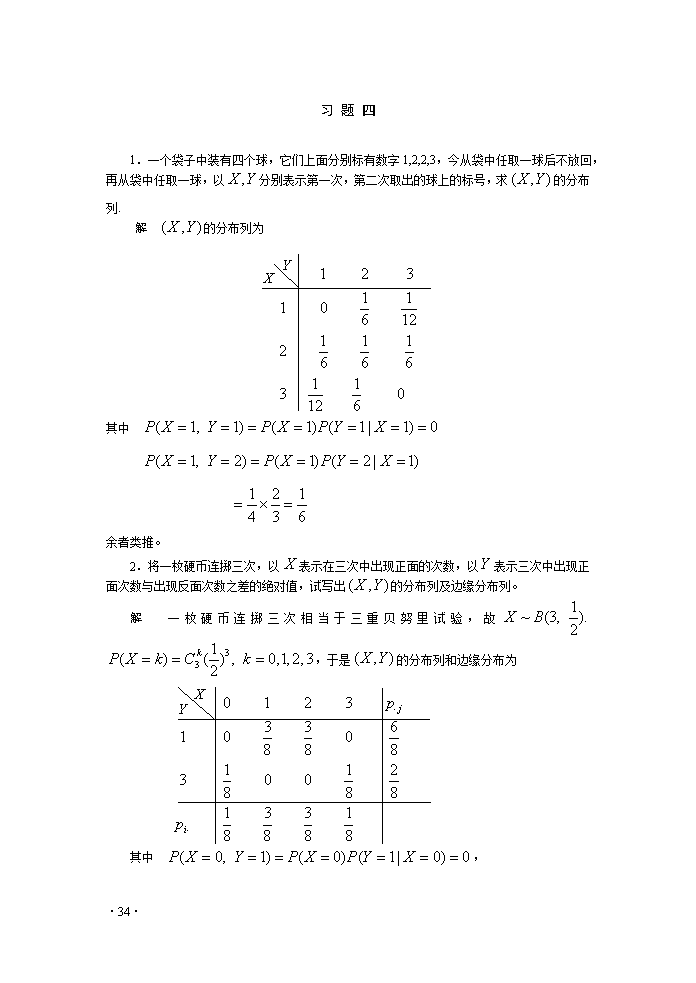
'习题四1.一个袋子中装有四个球,它们上面分别标有数字1,2,2,3,今从袋中任取一球后不放回,再从袋中任取一球,以分别表示第一次,第二次取出的球上的标号,求的分布列.解的分布列为YX其中余者类推。2.将一枚硬币连掷三次,以表示在三次中出现正面的次数,以表示三次中出现正面次数与出现反面次数之差的绝对值,试写出的分布列及边缘分布列。解一枚硬币连掷三次相当于三重贝努里试验,故,于是的分布列和边缘分布为YX其中,·54·
,余者类推。3.设的概率密度为又(1);(2)。求xx+y=3422y解(1);(2).4.设的概率密度为求(1)系数;(2)落在圆内的概率.解(1),.(2)设,所求概率为·54·
.5.已知随机变量和的联合概率密度为求和的联合分布函数.解1设的分布函数为,则解2由联合密度可见,独立,边缘密度分别为边缘分布函数分别为,则·54·
设的分布函数为,则yx10D6.设二维随机变量在区域,内服从均匀分布,求边缘概率密度。解的概率密度为关于和的密度为x+y=11yx0x=y7.设的概率密度为求边缘密度和概率解·54·
.8.一电子仪器由两个部件组成,以和分别表示两个部件的寿命(单位:千小时)已知的联合分布函数为:(1)问是否独立?为什么?(2)求两个部件的寿命都超过100小时的概率.解(1)先求边缘分布函数:因为,所以独立.(2).9.设的概率密度为间是否独立?解边缘密度为因为,所以独立.10.设的概率密度为·54·
y=x1yx0问是否独立.解边缘密度yx0因为,所以不独立。11.设的概率密度为试证明与不独立,但与是相互独立的。证先求的联合分布函数·54·
关于的边缘分布函数为关于的边缘分布函数为因为,所以不独立.再证与独立:设的联合分布函数为,则·54·
关于的边缘分布函数分别为因为,所以与独立.证2利用随机向量的变换(参见王梓坤《概率基础及其应用》83页)设.函数的反函数为的反函数为,;于是的概率密度函数为·54·
关于的边缘密度为关于的边缘密度为因为,所以独立.12.设随机变量与相互独立,下表列出了二维随机变量的联合分布律及关于和关于的边缘分布律中的部分数值,试将其余值填入表中空白处.1解设由联合分布和边缘分布的关系知由独立性,即,故,,,所以,所以的分布为·54·
113.已知随机变量和的概率分布为,而且(1)求和的联合分布;(2)问和是否独立?为什么?解(1)知,再由联合分布和边缘分布的关系知的分布为1(2)因,所以不独立.14.设随机变量相互独立,且都服从上的均匀分布,求方程有实根的概率.解设‘方程有实根’,则发生·54·
yxbb即,.yx当时,图形如下:15.已知随机变量和的联合分布为试求:(1)的概率分布;(2)的概率分布解(1)的分布为(2)的分布为16.设与为独立同分布的离散型随机变量,其概率分布列为,,求的分布列.解设,的分布为17.设是相互独立的随机变量,它们都服从参数为的二项分布,证明·54·
服从参数为的二项分布.证故服从参数为的二项分布.注:此处用到一个组合公式:此公式的正确性可直观地说明如下:从个不同的元素中取个共有种不同的取法。从另一个角度看,把个元素分布两部分,一部分有个,另一部分有个,从第一部分中取个再配上从第二部分中取个,不同的取法共,让从变到,总的取法是,这两种取法应相等.18.设相互独立,其概率密度分别为求的概率密度.解1设,由卷积分式,的概率密度为10zyD不等式确定平面域如图.当时,当时,当时,综上所述·54·
解2变量代换法:,注意到当时=1,有因所以,当时,,当时,,当时,.综上所述解3分布函数法:设的分布函数为,则yx+y=110xx+y=0·54·
的概率密度为L2L1LXY19.设部件的寿命,的寿命,按下图联结构成系统,即当部件损坏时,部件立即开始工作,求系统的寿命的概率密度.解的密度为的密度为设的密度为,则ozyx当时,当时,,当时综相所述的密度为.·54·
.20.设的概率密度为求的概率密度.解1利用的密度公式:,取得其中oyzyy不等式确定平面域如图当或时,当时,即解2设的分布函数为,密度为,则xyx-y=0x-y=zx-y=1·54·
于是21.设随机变量的概率密度为,求的概率密度.解设的分布函数为,则故,故22.设随机变量与独立,,,试求的概率密度解1由卷积公式其中不等式确定平面区域:·54·
xy0当时解2用变量代换:.因为所以当时.23.设随机变量的概率密度为求的分布函数.x+2y=zz>00xyx+2y=0解24.设二维随机变量在矩形上服从均匀分布,试求边长为和的矩形面积的概率密度.·54·
解1设矩形的面积为,则,又设的分布函数为,则其中oSxy=S,0
您可能关注的文档
- 周德庆微生物学课后习题答案.pdf
- 周德庆编《微生物学教程》课后习题参考答案.doc
- 周惠中微观经济学(第3版)课后习题答案.pdf
- 周炳坤激光原理课后习题答案 1-7.pdf
- 周炳琨激光原理第二章习题解答(完整版).doc
- 周霭如版 C++(4)(上)-习题解答(华工).docx
- 哈尔滨工程大学《辐射防护概论》课后题及其答案.doc
- 哈工大《离散数学》教科书习题答案.doc
- 哈工大传热学第五版课后习题答案.doc
- 哈工大理论力学第七版课后习题答案完整版.pdf
- 唐作藩《音韵学教程》练习答案.doc
- 唐文彦《传感器》习题答案.doc
- 唐朔飞版计算机组成原理_课后习题答案(答案精准).doc
- 唐策善+刘黄生+《数据结构——用C语言描述》+课后题答案.doc
- 商务礼仪试题全套及答案.docx
- 商务谈判课后答案.doc
- 商品学概论练习题材及答案.doc
- 商品学概论试题及答案(汇总).doc