- 1.68 MB
- 2022-04-29 14:11:53 发布
- 1、本文档共5页,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,可选择认领,认领后既往收益都归您。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细先通过免费阅读内容等途径辨别内容交易风险。如存在严重挂羊头卖狗肉之情形,可联系本站下载客服投诉处理。
- 文档侵权举报电话:19940600175。
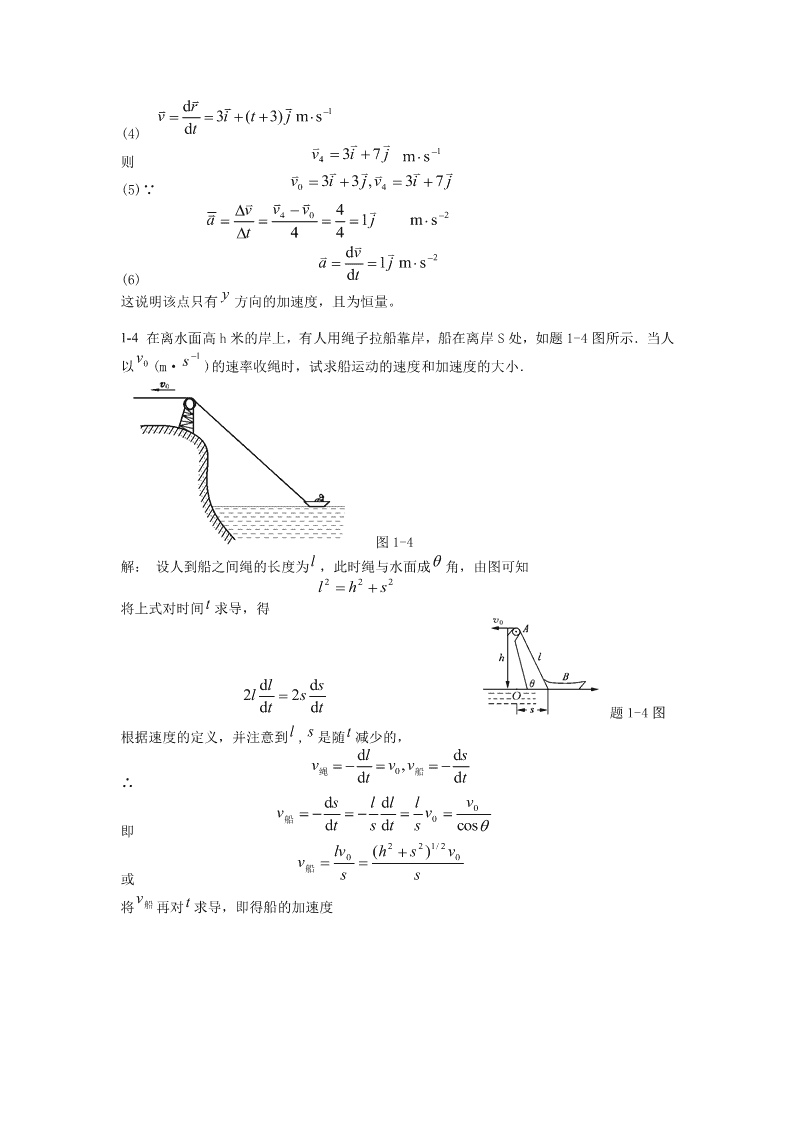
'大学物理简明教程习题解答习题一drdrdvdv1-1|r|与r有无不同?dt和dt有无不同?dt和dt有无不同?其不同在哪里?试举例说明.rrrrrrr解:(1)是位移的模,r是位矢的模的增量,即21,21;drdrdsdtdtvdt(2)是速度的模,即.drdt只是速度在径向上的分量.drdrdrˆrˆr∵有rrrˆ(式中rˆ叫做单位矢),则dtdtdtdr式中dt就是速度径向上的分量,drdr与dtdt∴不同如题1-1图所示.题1-1图dvdvdvadtdtdta(3)表示加速度的模,即,是加速度在切向上的分量.vv(∵有表轨道节线方向单位矢),所以dvdvdvdtdtdtdv式中dt就是加速度的切向分量.drˆdˆ与(dtdt的运算较复杂,超出教材规定,故不予讨论)xxtyyt1-2设质点的运动方程为=(),=(),在计算质点的速度和加速度时,有人先求2drdr22xyvdtadt2出r=,然后根据=,及=而求得结果;又有人先计算速度和加速度的分量,再合成求得结果,即222222dxdydxdy22vdtdtadtdt=及=你认为两种方法哪一种正确?为什么?两者差别何在?rxiyj解:后一种方法正确.因为速度与加速度都是矢量,在平面直角坐标系中,有,
drdxdyvijdtdtdtd2rd2xd2yaij222dtdtdt故它们的模即为2222dxdyvvxvydtdt222222dxdyaaaxydt2dt2而前一种方法的错误可能有两点,其一是概念上的错误,即误把速度、加速度定义作2drdrva2dtdt2drdrdr与2其二,可能是将dtdt误作速度与加速度的模。在1-1题中已说明dt不是速度的模,2dr2而只是速度在径向上的分量,同样,dt也不是加速度的模,它只是加速度在径向分量中22drda径2rdtdtr的一部分。或者概括性地说,前一种方法只考虑了位矢在径向(即量值)方面随时间的变化率,而没有考虑位矢r及速度v的方向随间的变化率对速度、加速度的贡献。xOy1-3一质点在平面上运动,运动方程为1x=3t+5,y=2t2+3t-4.式中t以s计,x,y以m计.(1)以时间t为变量,写出质点位置矢量的表示式;(2)求出t=1s时刻和t=2s时刻的位置矢量,计算这1秒内质点的位移;(3)计算t=0s时刻到t=4s时刻内的平均速度;(4)求出质点速度矢量表示式,计算t=4s时质点的速度;(5)计算t=0s到t=4s内质点的平均加速度;(6)求出质点加速度矢量的表示式,计算t=4s时质点的加速度(请把位置矢量、位移、平均速度、瞬时速度、平均加速度、瞬时加速度都表示成直角坐标系中的矢量式).12r(3t5)i(t3t4)j解:(1)2mt1t2(2)将,代入上式即有r8i0.5jm1r11j4jm2rrr3j4.5jm21r5j4j,r17i16j(3)∵04rr4r012i20j1v3i5jmst404∴
dr1v3i(t3)jms(4)dtv3i7jms1则4v3i3j,v3i7j(5)∵04vv4v042a1jmst44dv2a1jms(6)dty这说明该点只有方向的加速度,且为恒量。1-4在离水面高h米的岸上,有人用绳子拉船靠岸,船在离岸S处,如题1-4图所示.当人vs1以0(m·)的速率收绳时,试求船运动的速度和加速度的大小.图1-4l解:设人到船之间绳的长度为,此时绳与水面成角,由图可知222lhs将上式对时间t求导,得dlds2l2sdtdt题1-4图lst根据速度的定义,并注意到,是随减少的,dldsvv,v绳0船∴dtdtdsldllv0vv船0dtsdtscos即221/2lv(hs)v00v船或ssvt将船再对求导,即得船的加速度
dldssldvvslv船dtdt0船avv2020dtss2l2(s)v022shv023ss221-5质点沿x轴运动,其加速度和位置的关系为a=2+6x,a的单位为ms,x的单1xms位为m.质点在=0处,速度为10,试求质点在任何坐标处的速度值.dvdvdxdvav解:∵dtdxdtdx2dadx(26x)dx分离变量:123v2x2xc两边积分得2x0v010c50由题知,时,,∴31v2xx25ms∴21-6已知一质点作直线运动,其加速度为a=4+3tms,开始运动时,x=5m,v=0,求该质点在t=10s时的速度和位置.dva43t解:∵dtdv(43t)dt分离变量,得32v4ttc1积分,得2t0v00c10由题知,,,∴32v4tt故2dx32v4tt又因为dt232dx(4tt)dt分离变量,2213x2ttc2积分得2t0x05c25由题知,,∴213x2tt5故2t10s所以时321v41010190ms102213x210105705m102
31-7一质点沿半径为1m的圆周运动,运动方程为=2+3t,式中以弧度计,t以秒计,求:(1)t=2s(2)当加速度的方向和半径成45°角时,其角位移是多少?d2d9t,18t解:dtdt2t2saR118236ms(1)时,2222anR1(92)1296msatan45145οa(2)当加速度方向与半径成角时,有n222RR(9t)18t即亦即3232t23t232.67rad则解得9于是角位移为912vtbt01-8质点沿半径为R的圆周按s=2的规律运动,式中s为质点离圆周上某点的弧vbtt长,0,都是常量,求:(1)时刻质点的加速度;(2)为何值时,加速度在数值上等于b.dsvvbt0解:(1)dtdvabdt22v(vbt)0anRR4(vbt)2220aaabn2R则加速度与半径的夹角为aRbarctan2an(v0bt)(2)由题意应有4(vbt)20abb2R422(v0bt)4bb,(vbt)020即Rv0tbab∴当时,vms11-9以初速度0=20抛出一小球,抛出方向与水平面成幔60°的夹角,RR求:(1)球轨道最高点的曲率半径1;(2)落地处的曲率半径2.(提示:利用曲率半径与法向加速度之间的关系)
解:设小球所作抛物线轨道如题1-10图所示.题1-9图(1)在最高点,ovvvcos601x02ag10msn12v1an1又∵122v1(20cos60)1a10n110m∴(2)在落地点,vv20ms120,oagcos60而n222v2(20)80m2a10cos60∴n221-10飞轮半径为0.4m,自静止启动,其角加速度为β=0.2rad·s,求t=2s时边缘上各点的速度、法向加速度、切向加速度和合加速度.t2st0.220.41rads解:当时,1vR0.40.40.16ms则22aR0.4(0.4)0.0642nmsaR0.40.20.08ms222222aaa(0.064)(0.08)0.102msn1-11一船以速率v1=30km·h-1沿直线向东行驶,另一小艇在其前方以速率v2=40km·h-1沿直线向北行驶,问在船上看小艇的速度为何?在艇上看船的速度又为何?vvv解:(1)大船看小艇,则有2121,依题意作速度矢量图如题1-13图(a)题1-11图221vvv50kmh由图可知2112
v31arctanarctan36.87v4方向北偏西2vvv(2)小船看大船,则有1212,依题意作出速度矢量图如题1-13图(b),同上法,得v50112kmho36.87方向南偏东习题二2-1一个质量为P的质点,在光滑的固定斜面(倾角为)上以初速度v0运动,v0的方向与斜面底边的水平线AB平行,如图所示,求这质点的运动轨道.解:物体置于斜面上受到重力mg,斜面支持力N.建立坐标:取v0方向为X轴,平行斜面与X轴垂直方向为Y轴.如图2-2.题2-1图X方向:Fx0xv0t①FmgsinmaY方向:yy②t0时y0vy012ygsint2由①、②式消去t,得12ygsinx22v0xOyffy2-2质量为16kg的质点在平面内运动,受一恒力作用,力的分量为x=6N,=v-7N,当t=0时,xy0,vx=-2m·s-1,y=0.求当t=2s点的(1)位矢;(2)速度.fx63ams2x解:m168fy72amsym16(1)2351vvadt22msxx0x0842771vvadt2msyy0y01682s于是质点在时的速度571vijms48(2)
1212r(vtat)iatj0xy221317(224)i()4j28216137ijm48kvkt2-3质点在流体中作直线运动,受与速度成正比的阻力(为常数)作用,=0时质点的k()tvem速度为v0,证明(1)t时刻的速度为v=0;(2)由0到t的时间内经过的距离为mv0km()tv()xkm0tmk=()[1-e];(3)停止运动前经过的距离为k;(4)证明当时速1ve度减至0的,式中m为质点的质量.kvdva答:(1)∵mdt分离变量,得dvkdtvmvdvtkdt即v0v0mvktlnlnemv0ktvvem∴0tktmvktxvdtvemdt0(1em)00(2)k(3)质点停止运动时速度为零,即t→∞,ktmvxvemdt000k故有m(4)当t=k时,其速度为kmvvvemkve1000e1ve即速度减至0的.mv02-4一质量为的质点以与地的仰角=30°的初速从地面抛出,若忽略空气阻力,求质点落地时相对抛射时的动量的增量.解:依题意作出示意图如题2-6图
题2-4图在忽略空气阻力情况下,抛体落地瞬时的末速度大小与初速度大小相同,与轨道相切斜向下,yx30o而抛物线具有对轴对称性,故末速度与轴夹角亦为,则动量的增量为pmvmv0mv0由矢量图知,动量增量大小为,方向竖直向下.F(102t)it2-5作用在质量为10kg的物体上的力为N,式中的单位是s,(1)求4s后,这物体的动量和速度的变化,以及力给予物体的冲量.(2)为了使这力的冲量为200N·s,6j-1该力应在这物体上作用多久,试就一原来静止的物体和一个具有初速度m·s的物体,回答这两个问题.解:(1)若物体原来静止,则t41pFdt(102t)idt56kgmsi100x,沿轴正向,p11v5.6msi1m1Ip56kgmsi1116ms若物体原来具有初速,则tFtpmv,pm(vdt)mvFdt000000m于是tpppFdtp2010,同理,v2v1,I2I1这说明,只要力函数不变,作用时间相同,则不管物体有无初动量,也不管初动量有多大,那么物体获得的动量的增量(亦即冲量)就一定相同,这就是动量定理.(2)同上理,两种情况中的作用时间相同,即t2I(102t)dt10tt02t10t2000亦即t10st20s解得,(舍去)1vms2-6一颗子弹由枪口射出时速率为0,当子弹在枪筒内被加速时,它所受的合力为abta,btF=()N(为常数),其中以秒为单位:(1)假设子弹运行到枪口处合力刚好为零,试计算子弹走完枪筒全长所需时间;(2)求子弹所受的冲量.(3)求子弹的质量.解:(1)由题意,子弹到枪口时,有atF(abt)0b,得(2)子弹所受的冲量t12I(abt)dtatbt02
at将b代入,得2aI2b(3)由动量定理可求得子弹的质量2Iamv2bv00F合7i6jNr3i4j16kmF2-7设.(1)当一质点从原点运动到时,求所作的功.(2)如果质点到r处时需0.6s,试求平均功率.(3)如果质点的质量为1kg,试求动能的变化.F解:(1)由题知,合为恒力,AFr(7i6j)(3i4j16k)∴合212445JA45P75w(2)t0.6EA45J(3)由动能定理,kv0-1A2-8如题2-18图所示,一物体质量为2kg,以初速度=3m·s从斜面点处下滑,它与斜面的摩擦力为8N,到达B点后压缩弹簧20cm后停止,然后又被弹回,求弹簧的劲度系数和物体最后能回到的高度.解:取木块压缩弹簧至最短处的位置为重力势能零点,弹簧原长处为弹性势能零点。则由功能原理,有1212frskxmvmgssin372212mvmgssin37fsr2k12kx2s4.80.25mx0.2m式中,,再代入有关数据,解得-1k1390Nm题2-8图h再次运用功能原理,求木块弹回的高度o12fsmgssin37kxr2s1.4m代入有关数据,得,则木块弹回高度ohssin370.84m2-9一个小球与一质量相等的静止小球发生非对心弹性碰撞,试证碰后两小球的运动方向
互相垂直.证:两小球碰撞过程中,机械能守恒,有121212mvmvmv012222222vvv即012①题2-9图(a)题2-9图(b)又碰撞过程中,动量守恒,即有mvmvmv012vvv亦即012②v由②可作出矢量三角形如图(b),又由①式可知三矢量之间满足勾股定理,且以0为斜边,vv故知1与2是互相垂直的.mx1,y1vvxivyjx2-10一质量为的质点位于()处,速度为,质点受到一个沿负方向f的力的作用,求相对于坐标原点的角动量以及作用于质点上的力的力矩.解:由题知,质点的位矢为rxiyj11作用在质点上的力为ffi所以,质点对原点的角动量为Lrmv0(xiyi)m(vivj)11xy(xmvymv)k1y1x作用在质点上的力的力矩为Mrf(xiyj)(fi)yfk0111r1102-11哈雷彗星绕太阳运动的轨道是一个椭圆.它离太阳最近距离为=8.75×10m时的速率是v1=5.46×104m·s-1,它离太阳最远时的速率是v2=9.08×102m·s-1r阳的距离2多少?(太阳位于椭圆的一个焦点。)解:哈雷彗星绕太阳运动时受到太阳的引力——即有心力的作用,所以角动量守恒;又由于哈雷彗星在近日点及远日点时的速度都与轨道半径垂直,故有rmvrmv1122104r1v18.75105.461012r5.2610m22v29.0810∴12-12物体质量为3kg,t=0时位于r4im,vi6jms,如一恒力f5jN作用在物体上,求3秒后,(1)物体动量的变化;(2)相对z轴角动量的变化.
31pfdt5jdt15jkgms解:(1)0xxvt437(2)解(一)00x12152yvtat63325.5j0y223r4ir7i25.5j即1,2vv1x0x5vvat6311y0y3vi6jvi11j即11,2Lrmv4i3(i6j)72k∴111Lrmv(7i25.5j)3(i11j)154.5k22221LLL82.5kkgms∴21dzM解(二)∵dtttLMdt(rF)dt∴0031520(4t)i(6t)t)j5jdt2335(4t)kdt82.5kkgm2s10题2-12图mRO2-13飞轮的质量=60kg,半径=0.25m,绕其水平中心轴转动,转速为-1F900rev·min.现利用一制动的闸杆,在闸杆的一端加一竖直方向的制动力,可使飞轮减速.已知闸杆的尺寸如题2-25图所示,闸瓦与飞轮之间的摩擦系数=0.4,飞轮的转动惯量可按匀质圆盘计算.试求:(1)设F=100N,问可使飞轮在多长时间内停止转动?在这段时间里飞轮转了几转?(2)如果在2s内飞轮转速减少一半,需加多大的力F?NNFrFr解:(1)先作闸杆和飞轮的受力分析图(如图(b)).图中、是正压力,、是摩FFyARPO擦力,x和是杆在点转轴处所受支承力,是轮的重力,是轮在轴处所受支承力.
题2-13图(a)题2-13图(b)杆处于静止状态,所以对A点的合力矩应为零,设闸瓦厚度不计,则有ll12F(ll)Nl0NF121l1FR/I对飞轮,按转动定律有r,式中负号表示与角速度方向相反.FNNN∵rll12FNFrl∴112ImR,又∵2FR2(ll)r12FImRl∴1①F100N以等代入上式,得20.40(0.500.75)402100rads600.250.503由此可算出自施加制动闸开始到飞轮停止转动的时间为090023t7.06s6040这段时间内飞轮的角位移为129002914092tt()0260423453.12rad53.1可知在这段时间里,飞轮转了转.21900rads0(2)60,要求飞轮转速在t2s内减少一半,可知0015202radst2t2
用上面式(1)所示的关系,可求出所需的制动力为mRl1F2(ll)12600.250.501520.40(0.500.75)2177N2-14固定在一起的两个同轴均匀圆柱体可绕其光滑的水平对称轴OO转动.设大小圆柱体的半径分别为R和r,质量分别为M和m.绕在两柱体上的细绳分别与物体m1和m2相连,mmRrm1和2则挂在圆柱体的两侧,如题2-26图所示.设=0.20m,=0.10m,=4kg,M=10kg,m1=m2=2kg,且开始时m1,m2离地均为h=2m.求:(1)柱体转动时的角加速度;(2)两侧细绳的张力.aamm解:设1,2和β分别为1,2和柱体的加速度及角加速度,方向如图(如图b).题2-14(a)图题2-14(b)图mm(1)1,2和柱体的运动方程如下:Tmgma2222①mgTma1111②TRTrI12③TT,TT,ar,aR式中1122211212IMRmr而22由上式求得Rmrm12g22ImRmr120.220.129.8121222100.2040.1020.2020.102226.13rads(2)由①式
Tmrmg20.106.1329.820.8N222由②式TmgmR29.820.2.6.1317.1N111mlO2-15如题2-15图所示,一匀质细杆质量为,长为,可绕过一端的水平轴自由转动,杆于水平位置由静止开始摆下.求:(1)初始时刻的角加速度;(2)杆转过角时的角速度.解:(1)由转动定律,有112mg(ml)233g∴2l(2)由机械能守恒定律,有l1122mgsin(ml)2233gsinl∴题2-15图习题三3-1气体在平衡态时有何特征?气体的平衡态与力学中的平衡态有何不同?答:气体在平衡态时,系统与外界在宏观上无能量和物质的交换;系统的宏观性质不随时间变化.力学平衡态与热力学平衡态不同.当系统处于热平衡态时,组成系统的大量粒子仍在不停地、无规则地运动着,大量粒子运动的平均效果不变,这是一种动态平衡.而个别粒子所受合外力可以不为零.而力学平衡态时,物体保持静止或匀速直线运动,所受合外力为零.3-2气体动理论的研究对象是什么?理想气体的宏观模型和微观模型各如何?答:气体动理论的研究对象是大量微观粒子组成的系统.是从物质的微观结构和分子运动论出发,运用力学规律,通过统计平均的办法,求出热运动的宏观结果,再由实验确认的方法.从宏观看,在温度不太低,压强不大时,实际气体都可近似地当作理想气体来处理,压强越低,温度越高,这种近似的准确度越高.理想气体的微观模型是把分子看成弹性的自由运动的质点.3-3温度概念的适用条件是什么?温度微观本质是什么?答:温度是大量分子无规则热运动的集体表现,是一个统计概念,对个别分子无意义.温度微观本质是分子平均平动动能的量度.3-4计算下列一组粒子平均速率和方均根速率?Ni214682
1Vi(ms)10.020.030.040.050.0解:平均速率NiViVNi2110420630840250214682890121.7ms41方均根速率22NiViVNi223222110420610840250214682125.6ms3-5速率分布函数f(v)的物理意义是什么?试说明下列各量的物理意义(n为分子数密度,N为系统总分子数).(1)f(v)dv(2)nf(v)dv(3)Nf(v)dvvv2(4)0f(v)dv(5)0f(v)dv(6)vNf(v)dv1解:f(v):表示一定质量的气体,在温度为T的平衡态时,分布在速率v附近单位速率区间内的分子数占总分子数的百分比.(1)f(v)dv:表示分布在速率v附近,速率区间dv内的分子数占总分子数的百分比.(2)nf(v)dv:表示分布在速率v附近、速率区间dv内的分子数密度.(3)Nf(v)dv:表示分布在速率v附近、速率区间dv内的分子数.v(4)f(v)dv:表示分布在v1~v2区间内的分子数占总分子数的百分比.0(5)f(v)dv:表示分布在0~的速率区间内所有分子,其与总分子数的比值是1.0v2(6)Nf(v)dv:表示分布在v1~v2区间内的分子数.v13-6题3-6图(a)是氢和氧在同一温度下的两条麦克斯韦速率分布曲线,哪一条代表氢?题3-6图(b)是某种气体在不同温度下的两条麦克斯韦速率分布曲线,哪一条的温度较高?答:图(a)中(1)表示氧,(2)表示氢;图(b)中(2)温度高.题3-6图3-7试说明下列各量的物理意义.
13i(1)kT(2)kT(3)kT222Mii3(4)RT(5)RT(6)RTM222mol1解:(1)在平衡态下,分子热运动能量平均地分配在分子每一个自由度上的能量均为kT.23(2)在平衡态下,分子平均平动动能均为kT.2i(3)在平衡态下,自由度为i的分子平均总能量均为kT.2Mi(4)由质量为M,摩尔质量为M,自由度为i的分子组成的系统的内能为RT.molM2moli(5)1摩尔自由度为i的分子组成的系统内能为RT.23(6)1摩尔自由度为3的分子组成的系统的内能RT,或者说热力学体系内,1摩尔分子23的平均平动动能之总和为RT.23-8有一水银气压计,当水银柱为0.76m高时,管顶离水银柱液面0.12m,管的截面积为-422.0×10m,当有少量氦(He)混入水银管内顶部,水银柱高下降为0.6m,此时温度为-127℃,试计算有多少质量氦气在管顶(He的摩尔质量为0.004kg·mol)?M解:由理想气体状态方程pVRT得MmolpVMMmolRT53汞的重度dHg1.3310Nm氦气的压强P(0.760.60)dHg43氦气的体积V(0.880.60)2.010m4(0.760.60)d(0.282.010)HgM0.004R(27327)4(0.760.60)d(0.282.010)Hg0.0048.31(27327)61.9110Kg3-9设有N个粒子的系统,其速率分布如题6-18图所示.求(1)分布函数f(v)的表达式;(2)a与v之间的关系;0(3)速度在1.5v到2.0v之间的粒子数.00(4)粒子的平均速率.(5)0.5v到1v区间内粒子平均速率.00
题3-9图解:(1)从图上可得分布函数表达式Nf(v)av/v0(0vv0)Nf(v)a(v0v2v0)Nf(v)0(v2v)0av/Nv0(0vv0)f(v)a/N(v0v2v0)0(v2v)0f(v)满足归一化条件,但这里纵坐标是Nf(v)而不是f(v)故曲线下的总面积为N,(2)由归一化条件可得v0av2v02NNdvNadvNa0vv03v001(3)可通过面积计算Na(2v01.5v0)N3(4)N个粒子平均速率21v0av2v0v0vf(v)dv0vNf(v)dv0dvvavdvNv001123211v(av0av0)v0N329(5)0.5v到1v区间内粒子平均速率00v0vdN0.5v0Nv0vdNvNN0.5v0N112Nv0Nv0avvf(v)dvdvN0.5v0N0.5v0Nv11023321v0av1avav17av000vdv()N0.5v0vN3v24vN241010010.5v到1v区间内粒子数00131N1(a0.5a)(v00.5v0)av0N28427av7v00v6N9113-10试计算理想气体分子热运动速率的大小介于vpvp100与vpvp100之间的分子数占总分子数的百分比.v解:令u,则麦克斯韦速率分布函数可表示为vP
dN42u2ueduN因为u1,u0.02N42u2由ueu得NN411e0.021.66%N3-111mol氢气,在温度为27℃时,它的平动动能、转动动能和内能各是多少?解:理想气体分子的能量iERT23平动动能t3Et8.313003739.5J22转动动能r2Er8.313002493J25内能i5Ei8.313006232.5J2-3-53-12一真空管的真空度约为1.38×10Pa(即1.0×10mmHg),试求在27℃时单位体积中-10的分子数及分子的平均自由程(设分子的有效直径d=3×10m).解:由气体状态方程pnkT得3p1.3810173n3.3310m23kT1.38103001由平均自由程公式22dn17.5m201729103.3310-43-13(1)求氮气在标准状态下的平均碰撞频率;(2)若温度不变,气压降到1.33×10Pa,-10平均碰撞频率又为多少(设分子有效直径10m)?2解:(1)碰撞频率公式z2dnv对于理想气体有pnkT,即pnkT22dvp所以有zkTRT8.312731而v1.60v1.60455.43msM28mol氮气在标准状态下的平均碰撞频率205210455.431.0131081z5.4410s01.3810273气压下降后的平均碰撞频率204210455.431.33101z0.714s231.3810273
3-141mol氧气从初态出发,经过等容升压过程,压强增大为原来的2倍,然后又经过等温膨胀过程,体积增大为原来的2倍,求末态与初态之间(1)气体分子方均根速率之比;(2)分子平均自由程之比.解:由气体状态方程pp12及pVpV2233TT122RT方均根速率公式v1.73Mmol2v初T1p11v2Tp2末22p对于理想气体,pnkT,即nkTkT所以有22dp初T1p21pT末12习题四4-1下列表述是否正确?为什么?并将错误更正.QEpdVQEA(1)(2)QQ2211不可逆QQ(3)1(4)1QEA解:(1)不正确,QΔEpdV(2)不正确,Q21Q(3)不正确,1Q21不可逆Q(4)不正确,1pV4-2用热力学第一定律和第二定律分别证明,在图上一绝热线与一等温线不能有两个交点.题4-2图解:1.由热力学第一定律有
QEAab若有两个交点和,则ab经等温过程有EQA0111ab经绝热过程EA021EA022EEab从上得出12,这与,两点的内能变化应该相同矛盾.2.若两条曲线有两个交点,则组成闭合曲线而构成了一循环过程,这循环过程只有吸热,无100%放热,且对外做正功,热机效率为,违背了热力学第二定律.4-3一循环过程如题4-3图所示,试指出:ab,bc,ca(1)各是什么过程;pV(2)画出对应的图;(3)该循环是否是正循环?(4)该循环作的功是否等于直角三角形面积?Q,Q,Q(5)用图中的热量abbcac表述其热机效率或致冷系数.ab解:(1)是等体过程bcVKTK过程:从图知有,为斜率pVvRT由得vRpKbc故过程为等压过程ca是等温过程pV(2)图如题4-3’图题4-3’图(3)该循环是逆循环pV(4)该循环作的功不等于直角三角形面积,因为直角三角形不是图中的图形.QabeQQQ(5)bccaab
题4-3图题4-4图4-4两个卡诺循环如题4-4图所示,它们的循环面积相等,试问:(1)它们吸热和放热的差值是否相同;(2)对外作的净功是否相等;(3)效率是否相同?答:由于卡诺循环曲线所包围的面积相等,系统对外所作的净功相等,也就是吸热和放热的差值相等.但吸热和放热的多少不一定相等,效率也就不相同.BdQBdQ可逆不可逆SSSSBAABAA4-5根据T及T,这是否说明可逆过程的熵变大于不可逆过程熵变?为什么?说明理由.答:这不能说明可逆过程的熵变大于不可逆过程熵变,熵是状态函数,熵变只与初末状态有关,如果可逆过程和不可逆过程初末状态相同,具有相同的熵变.只能说在不可逆过程中,系统的热温比之和小于熵变.aacb4-6如题4-6图所示,一系统由状态沿到达状态b的过程中,有350J热量传入系统,而系统作功126J.adb(1)若沿时,系统作功42J,问有多少热量传入系统?bbaa(2)若系统由状态沿曲线返回状态时,外界对系统作功为84J,试问系统是吸热还是放热?热量传递是多少?题4-6图abcba解:由过程可求出态和态的内能之差QEAEQA350126224JabdA42J过程,系统作功QEA22442266J系统吸收热量baA84J过程,外界对系统作功QEA22484308J系统放热4-71mol单原子理想气体从300K加热到350K,问在下列两过程中吸收了多少热量?增加了多少内能?对外作了多少功?(1)体积保持不变;(2)压力保持不变.解:(1)等体过程QE由热力学第一定律得
iQEC(TT)R(TT)V2121吸热23QE8.31(350300)623.252J对外作功A0(2)等压过程i2QC(TT)R(TT)P212125Q8.31(350300)1038.75吸热2JEC(TT)V213E8.31(350300)623.25内能增加2JAQE1038.75623.5415.5J对外作功34-80.01m氮气在温度为300K时,由0.1MPa(即1atm)压缩到10MPa.试分别求氮气经等温及绝热压缩后的(1)体积;(2)温度;(3)各过程对外所作的功.T300K解:(1)等温压缩pVpV由1122求得体积p1V113V0.011102p1032m对外作功Vp21AVRTlnpVln1Vp12511.013100.01ln0.0134.6710J57CRV(2)绝热压缩25p1V11/V()2由绝热方程p1V1p2V2p21p1V11/p1V()()V21pp221143()0.011.931010m1TpTp由绝热方程1122得1T1p21.40.4T300(10)T579K212p1QEAQ0热力学第一定律,MAC(TT)V21M所以mol
Mp1V15pVRTAR(TT)21MRT2mol,151.013100.00153A(579300)23.5103002Jabab4-91mol的理想气体的T-V图如题4-9图所示,为直线,延长线通过原点O.求过程气体对外做的功.题4-9图TKVK解:设由图可求得直线的斜率为T0K2V0T0KV2V得过程方程0pVRT由状态方程RTp得Vab过程气体对外作功2V0ApdVv02V0RT2V0RT0AdVVdVv0VV0V2V02V0RTRT00dVV02V204-10一卡诺热机在1000K和300K的两热源之间工作,试计算(1)热机效率;(2)若低温热源不变,要使热机效率提高到80%,则高温热源温度需提高多少?(3)若高温热源不变,要使热机效率提高到80%,则低温热源温度需降低多少?T21T解:(1)卡诺热机效率1300170%1000(2)低温热源温度不变时,若300180%T1T1500500K要求1K,高温热源温度需提高(3)高温热源温度不变时,若
T2180%1000T200100K要求2K,低温热源温度需降低4-11如题4-11图所示是一理想气体所经历的循环过程,其中AB和CD是等压过程,BC和DA为绝热过程,已知B点和C点的温度分别为T2和T3.求此循环效率.这是卡诺循环吗?题4-11图Q21Q解:(1)热机效率1AB等压过程Q1CP(T2T1)MQC(TT)1PBAM吸热molCDQ2vCP(T2T1)等压过程MQQC(TT)22PCDM放热molQTTT(1T/T)2CDCDCQTTT(1T/T)1BABAB根据绝热过程方程得到11AD绝热过程pATApDTD111BC绝热过程pBTBpCTCTTDppppABCDTT又CBT31T2(2)不是卡诺循环,因为不是工作在两个恒定的热源之间.4-12(1)用一卡诺循环的致冷机从7℃的热源中提取1000J的热量传向27℃的热源,需要多少功?从-173℃向27℃呢?(2)一可逆的卡诺机,作热机使用时,如果工作的两热源的温度差愈大,则对于作功就愈有利.当作致冷机使用时,如果两热源的温度差愈大,对于致冷是否也愈有利?为什么?解:(1)卡诺循环的致冷机QT22eATT静12727℃→℃时,需作功T1T2300280AQ100071.412T2280J17327℃→℃时,需作功
T1T2300100AQ1000200022T2100J(2)从上面计算可看到,当高温热源温度一定时,低温热源温度越低,温度差愈大,提取同样的热量,则所需作功也越多,对致冷是不利的.V20L,T300K4-13如题4-13图所示,1mol双原子分子理想气体,从初态11经历三V40L,T300K种不同的过程到达末态22.图中1→2为等温线,1→4为绝热线,4→2为等压线,1→3为等压线,3→2为等体线.试分别沿这三种过程计算气体的熵变.题4-13图12解:熵变dQdAdApdV等温过程,pVRT2dQ1V2RT1SSdV211VTT11VV2SSRlnRln25.7621VJ1!K123熵变3dQ2dQSS2113TTT3CdTT2CdTTTpV32SSClnCln21TTpV1T3TT1T3VV1213等压过程p1p3T1T3TV32TV11pp3232T3T2等体过程TpTp2222TpTp3331Vp22SSClnCln21PVVp1112p1V1p2V2在等温过程中VVV222SSClnClnRlnRln221PVVVV所以111
142熵变4dQ2dQSS2114TTT2CpdTT2T1SS0ClnCln21ppT4TTT4414绝热过程111T1V4TVTV11441TV41V4p11/p11/pVpV,()()1144Vpp14212p1V1p2V2在等温过程中V4p11/p11/V21/()()()VppV14211T1V2()TV41T1V12SSClnClnRln221PPTV41TTTT4-14有两个相同体积的容器,分别装有1mol的水,初始温度分别为1和2,1>2,令其进行接触,最后达到相同温度T.求熵的变化,(设水的摩尔热容为Cmol).解:两个容器中的总熵变TCdTTCdTmolmolSS0TT1T2T2TTTC(lnln)ClnmolmolTTTT1212因为是两个相同体积的容器,故C(TT)C(TT)mol2mol1TT21T得22(TT)21SSCln0mol4TT12kg4-15把0℃的0.5的冰块加热到它全部溶化成0℃的水,问:(1)水的熵变如何?(2)若热源是温度为20℃的庞大物体,那么热源的熵变化多大?1334Jg(3)水和热源的总熵变多大?增加还是减少?(水的熔解热)解:(1)水的熵变3Q0.533410S6121J1T273K(2)热源的熵变3Q0.533410S5702J1T293K
(3)总熵变SSS61257042J112K熵增加习题五q5-1电量都是的三个点电荷,分别放在正三角形的三个顶点.试问:(1)在这三角形的中心放一个什么样的电荷,就可以使这四个电荷都达到平衡(即每个电荷受其他三个电荷的库仑力之和都为零)?(2)这种平衡与三角形的边长有无关系?解:如题8-1图示(1)以A处点电荷为研究对象,由力平衡知:q为负电荷21q1qq2cos3024π0a4π032(a)33qq解得3(2)与三角形边长无关.题5-1图题5-2图ml5-2两小球的质量都是,都用长为的细绳挂在同一点,它们带有相同电量,静止时两线夹角为2,如题5-2图所示.设小球的半径和线的质量都可以忽略不计,求每个小球所带的电量.解:如题8-2图示Tcosmg21qTsinFe24π0(2lsin)q2lsin4mgtan解得05-3在真空中有A,B两平行板,相对距离为d,板面积为S,其带电量分别为+q和-q.则2qqE2这两板之间有相互作用力f,有人说f=40d,又有人说,因为f=qE,0S,所2qfSf以=0.试问这两种说法对吗?为什么?到底应等于多少?解:题中的两种说法均不对.第一种说法中把两带电板视为点电荷是不对的,第二种说法把qES合场强0看成是一个带电板在另一带电板处的场强也是不对的.正确解答应为一个
2qqqEfq板的电场为20S,另一板受它的作用力20S20S,这是两板间相互作用的电场力.l-9-15-4长=15.0cmAB上均匀地分布着线密度=5.0x10C·maP(1)在导线的延长线上与导线B端相距1=5.0cm处点的场强;(2)在导线的垂直平分线上dQ与导线中点相距2=5.0cm处点的场强.解:如题5-4-图所示题5-4图dxdqP(1)在带电直线上取线元,其上电量在点产生场强为1dxdEP24π0(ax)ldxEdE2PPl24π(ax)0211[]4πll0aa22l22π(4al)091用l15cm,5.010Cm,a12.5cm代入得21EP6.7410NC方向水平向右1dxdEQ224π0xd2(2)同理方向如题8-6图所示ldEQx0EQy由于对称性,即只有分量,21dxddEQy224πxdx2202d2∵ldxd2EdE2l3QylQy4π2(x2d2)222l222πl4d02915.010Ccml15cmd25cm以,,代入得
2EE14.96101QQyNC,方向沿y轴正向q5-5(1)点电荷位于一边长为a的立方体中心,试求在该点电荷电场中穿过立方体的一个面的电通量;(2)如果该场源点电荷移动到该立方体的一个顶点上,这时穿过立方体各面qq的电通量是多少?*(3)如题5-5(3)图所示,在点电荷的电场中取半径为R的圆平面.在Rarctan该平面轴线上的A点处,求:通过圆平面的电通量.(x)qEdSs解:(1)由高斯定理0q立方体六个面,当在立方体中心时,每个面上电通量相等qe6∴各面电通量0.2aq2a(2)电荷在顶点时,将立方体延伸为边长的立方体,使处于边长的立方体中心,则qe2a60边长的正方形上电通量qeaq240对于边长的正方形,如果它不包含所在的顶点,则,qe0如果它包含所在顶点则.如题5-5(a)图所示.题5-5(3)图题5-5(a)图题5-5(b)图题5-5(c)图22RRx(3)∵通过半径为的圆平面的电通量等于通过半径为的球冠面的电通量,球冠面积*22xS2π(Rx)[1]22Rxq0Sqx14π(R2x2)222∴00[Rx]*关于球冠面积的计算:见题8-9(c)图S2πrsinrd022πrsind022πr(1cos)510-35-6均匀带电球壳内半径6cm,外半径10cm,电荷体密度为2×C·m求距球心5cm,
8cm,12cm各点的场强.q2qEdSE4πrs解:高斯定理0,0当r5cm时,q0,E04πp3r3r8cm时,q3(r内)4π32rr内3E4πr241∴03.4810NC,方向沿半径向外.4πq(r3r3)r12cm时,3外内4π33rr外内34E4.10104πr21∴0NC沿半径向外.RRRR5-7半径为1和2(2>1)的两无限长同轴圆柱面,单位长度上分别带有电量和-,试求:(1)r<R1;(2)R1<r<R2;(3)r>R2处各点的场强.qEdSs解:高斯定理0S2πrl取同轴圆柱形高斯面,侧面积EdSE2πrl则SrRq0,E0对(1)1RrRql(2)12E2πr∴0沿径向向外rRq0(3)2E0∴题5-8图5-8两个无限大的平行平面都均匀带电,电荷的面密度分别为1和2,试求空间各处场强.解:如题8-12图示,两带电平面均匀带电,电荷面密度分别为1与2,1E()n122两面间,0
1E()n121面外,201E()n122面外,20n:垂直于两平面由1面指为2面.题5-9图5-9如题5-9图所示,在A,B两点处放有电量分别为+q,-q的点电荷,AB间距离为2R,现将另一正试验点电荷q0从O点经过半圆弧移到C点,求移动过程中电场力作的功.解:如题8-16图示1qqU()0O4π0RR1qqqUO()4π03RR6π0RqqoAq(UU)0OC6πR∴05-10如题5-10图所示的绝缘细线上均匀分布着线密度为的正电荷,两直导线的长度和半圆环的半径都等于R.试求环中心O点处的场强和电势.解:(1)由于电荷均匀分布与对称性,AB和CD段电荷在O点产生的场强互相抵消,取dlRddqRdOdEOy则产生点如图,由于对称性,点场强沿轴负方向题5-10图RdEdE2cosy24πR20sin()sin4π0R22[]2πR0(2)AB电荷在O点产生电势,以U0Adx2RdxUln21BR4πx4πx4π000
Uln22CD4π0同理产生πRU34πR4半圆环产生00UUUUln2O1232π4∴005-11三个平行金属板A,B和C的面积都是200cm2,A和B相距4.0mm,A与C相距2.0mm.B,C都接地,如题8-22图所示.如果使A板带正电3.0×10-7C,略去边缘效应,问B板和C板上的感应电荷各是多少?以地的电势为零,则A板的电势是多少?解:如题8-22图示,令A板左侧面电荷面密度为1,右侧面电荷面密度为2题5-11图UU(1)∵ACAB,即EdEd∴ACACABABEd1ACAB2Ed∴2ABACqAS且1+2q2qAA,21得3S3S27qSq210C1A而3C7qS110CB2(2)13UEdd2.310AACACAC0VRRRRq5-12两个半径分别为1和2(1<2)的同心薄金属球壳,现给内球壳带电+,试计算:(1)外球壳上的电荷分布及电势大小;(2)先把外球壳接地,然后断开接地线重新绝缘,此时外球壳的电荷分布及电势;*(3)再使内球壳接地,此时内球壳上的电荷以及外球壳上的电势的改变量.qqq解:(1)内球带电;球壳内表面带电则为,外表面带电为,且均匀分布,其电势
题5-12图qdrqUEdrRR2224π0r4π0Rqq(2)外壳接地时,外表面电荷入地,外表面不带电,内表面电荷仍为.所以球壳电qq势由内球与内表面产生:qqU04πR4πR0202qqqq(3)设此时内球壳带电量为;则外壳内表面带电量为,外壳外表面带电量为(电荷守恒),此时内球壳电势为零,且q"q"qq"U0A4πR4πR4πR010202R1qqR得2外球壳上电势q"q"qq"R1R2qUB24π0R24π0R24π0R24π0R2RR5-13在半径为1的金属球之外包有一层外半径为2的均匀电介质球壳,介质相对介电常Q数为r,金属球带电.试求:(1)电介质内、外的场强;(2)电介质层内、外的电势;(3)金属球的电势.DdSq解:利用有介质时的高斯定理S(RrR)(1)介质内12场强QrQrD,E3内34πr4πr0r;(rR)介质外2场强QrQrD,E3外34πr4πr0(rR)(2)介质外2电势QUEdr外r4πr0(RrR)介质内12电势UEdrEdrr内r外
q11Q()4πrR4πR0r202Q11r()4πrR0r2(3)金属球的电势R2UEdrEdrR内R外12R2QdrQdrR2R24π0rr24π0rQ11r()4πRR0r12题5-14图lR1R2R2R1lR2R15-14两个同轴的圆柱面,长度均为,半径分别为和(>),且>>-,QQ两柱面之间充有介电常数的均匀电介质.当两圆柱面分别带等量异号电荷和-时,求:(1)在半径r处/R1<r<R2/,厚度为dr,长为l的圆柱薄壳中任一点的电场能量密度和整个薄壳中的电场能量;(2)电介质中的总电场能量;(3)圆柱形电容器的电容.解:取半径为r的同轴圆柱面(S)DdS2πrlD(S)则(RrR)qQ当12时,QD∴2πrl22DQw222(1)电场能量密度28πrl22QQdrdWwd2πrdrl222薄壳中8πrl4πrl(2)电介质中总电场能量22R2QdrQR2WdWlnVR14πrl4πlR12QW(3)电容:∵2C
2Q2πlC2Wln(R/R)∴21题5-15图CCCC5-15如题5-15图所示,1=0.25F,2=0.15F,3=0.20F.1上电压为50V.求:UAB.C解:电容1上电量QCU111CCCCC电容2与3并联2323QQ其上电荷231Q23C1U12550U2CC35∴232325UUU50(1)86AB1235V习题六6-1在同一磁感应线上,各点B的数值是否都相等?为何不把作用于运动电荷的磁力方向定义为磁感应强度B的方向?解:在同一磁感应线上,各点B的数值一般不相等.因为磁场作用于运动电荷的磁力方向不仅与磁感应强度B的方向有关,而且与电荷速度方向有关,即磁力方向并不是唯一由磁场决定的,所以不把磁力方向定义为B的方向.6-2用安培环路定理能否求有限长一段载流直导线周围的磁场?答:不能,因为有限长载流直导线周围磁场虽然有轴对称性,但不是稳恒电流,安培环路定理并不适用.B2.0-2x6-3已知磁感应强度Wb·m轴正方向,如题9-6图所示.试求:(1)通过图中abcd面的磁通量;(2)通过图中befc面的磁通量;(3)通过图中aefd面的磁通量.解:如题9-6图所示题6-3图(1)通过abcd面积S1的磁通是BS2.00.30.40.24Wb11(2)通过befc面积S2的磁通量BS022
(3)通过aefd面积S的磁通量343BS320.30.5cos20.30.50.24Wb(或曰0.24Wb)5题6-4图6-4如题6-4图所示,AB、CD为长直导线,BC为圆心在O点的一段圆弧形导线,其半径为R.若通以电流I,求O点的磁感应强度.解:如题9-7图所示,O点磁场由AB、BC、CD三部分电流产生.其中AB产生B01I0CD产生B2,方向垂直向里12R0I0I3CD段产生B3(sin90sin60)(1),方向向里R2R2420I3∴B0B1B2B3(1),方向向里.2R266-5在真空中,有两根互相平行的无限长直导线L1和L2,相距0.1m,通有方向相反的电流,I1=20A,I2=10A,如题9-8图所示.A,B两点与导线在同一平面内.这两点与导线L2的距离均为5.0cm.试求A,B两点处的磁感应强度,以及磁感应强度为零的点的位置.题6-5图解:如题6-5图所示,B方向垂直纸面向里A0I10I24BA1.210T2(0.10.05)20.05(2)设B0在L2外侧距离L2为r处II02则02(r0.1)2r解得r0.1m题6-6图6-6如题6-6图所示,两根导线沿半径方向引向铁环上的A,B两点,并在很远处与电源相连.已知圆环的粗细均匀,求环中心O的磁感应强度.
解:如题9-9图所示,圆心O点磁场由直电流A和B及两段圆弧上电流I1与I2所产生,但A和B在O点产生的磁场为零。且I电阻R12.I电阻R221I1产生B1方向纸面向外0I1(2)B1,2R2I2产生B2方向纸面向里0I2B22R2BI(2)11∴1BI22有B0B1B206-7设题6-7图中两导线中的电流均为8A,对图示的三条闭合曲线a,b,c,分别写出安培环路定理等式右边电流的代数和.并讨论:(1)在各条闭合曲线上,各点的磁感应强度B的大小是否相等?(2)在闭合曲线c上各点的B是否为零?为什么?解:Bdl80aBdl80baBdl0c(1)在各条闭合曲线上,各点B的大小不相等.(2)在闭合曲线C上各点B不为零.只是B的环路积分为零而非每点B0.题6-7图6-8一根很长的同轴电缆,由一导体圆柱(半径为a)和一同轴的导体圆管(内、外半径分别为b,c)构成,如题6-8图所示.使用时,电流I从一导体流去,从另一导体流回.设电流都是均匀地分布在导体的横截面上,求:(1)导体圆柱内(r<a),(2)两导体之间(a<r<b),(3)导体圆筒内(b<r<c)以及(4)电缆外(r>c)各点处磁感应强度的大小解:Bdl0IL2Ir(1)raB2r02RIr0B22R(2)arbB2r0II0B2r
22rb(3)brcB2rII0220cb22I(cr)0B222r(cb)(4)rcB2r0B0题6-8图题6-9图6-9在磁感应强度为B的均匀磁场中,垂直于磁场方向的平面内有一段载流弯曲导线,电流为I,如题6-9图所示.求其所受的安培力.解:在曲线上取dlb则FabIdlBa∵dl与B夹角dl,B不变,B是均匀的.2bb∴FabIdlBI(dl)BIabBaa方向⊥ab向上,大小FBIabab题6-10图6-10如题6-10图所示,在长直导线AB内通以电流I1=20A,在矩形线圈CDEF中通有电流I2=10A,AB与线圈共面,且CD,EF都与AB平行.已知a=9.0cm,b=20.0cm,d=1.0cm,求:(1)导线AB的磁场对矩形线圈每边所作用的力;(2)矩形线圈所受合力和合力矩.解:(1)FCD方向垂直CD向左,大小0I14FCDI2b8.010N2d同理FFE方向垂直FE向右,大小0I15FFEI2b8.010N2(da)FCF方向垂直CF向上,大小为
da0I1I20I1I2da5FCFdrln9.210Nd2r2dF方向垂直ED向下,大小为ED5FEDFCF9.210N(2)合力FFCDFFEFCFFED方向向左,大小为4F7.210N合力矩MPmB∵线圈与导线共面∴Pm//BM0.6-11一正方形线圈,由细导线做成,边长为a,共有N匝,可以绕通过其相对两边中点的一个竖直轴自由转动.现在线圈中通有电流I,并把线圈放在均匀的水平外磁场B中,线圈对其转轴的转动惯量为J.求线圈绕其平衡位置作微小振动时的振动周期T.解:设微振动时线圈振动角度为(Pm,B),则2MPmBsinNIaBsin2d22由转动定律JNIaBsinNIaB2at22dNIaB即02dtJ2NIaB∴振动角频率J2J周期T22NaIB6-12一长直导线通有电流I1=20A,旁边放一导线ab,其中通有电流I2=10A,且两者共面,如6-12图所示.求导线ab所受作用力对O点的力矩.解:在ab上取dr,它受力dFab向上,大小为I01dFI2dr2rdF对O点力矩dMrFdM方向垂直纸面向外,大小为II012dMrdFdr2b0I1I2b6MdMdr3.610Nma2a题6-12图
B-4rB6-13电子在=70×10T=3.0cm.已知垂直于纸面向外,某时刻电子在A点,速度v向上,如题6-13图.(1)试画出这电子运动的轨道;(2)求这电子速度v的大小;(3)求这电子的动能E.k题6-13图解:(1)轨迹如图2v(2)∵evBmreBr71∴v3.710msm1216(3)EKmv6.210J2题6-14图6-14题6-14图中的三条线表示三种不同磁介质的BH关系曲线,虚线是B=H关系0的曲线,试指出哪一条是表示顺磁质?哪一条是表示抗磁质?哪一条是表示铁磁质?答:曲线Ⅱ是顺磁质,曲线Ⅲ是抗磁质,曲线Ⅰ是铁磁质.6-15螺绕环中心周长L=10cm,环上线圈匝数N=200匝,线圈中通有电流I=100mA.(1)当管内是真空时,求管中心的磁场强度H和磁感应强度B0;(2)若环内充满相对磁导率r=4200的磁性物质,则管内的B和H各是多少?*(3)磁性物质中心处由导线中传导电流产生的B0和由磁化电流产生的B′各是多少?解:(1)HdlIlHLNINI1H200AmL4B00H2.510T1(2)H200AmBHH1.05Tro4(3)由传导电流产生的B0即(1)中的B02.510T∴由磁化电流产生的BBB1.05T0习题七
7-1一半径r=10cmB=0.8T的均匀磁场中.回路平面与B垂直.当回路dr-1半径以恒定速率=80cm·s收缩时,求回路中感应电动势的大小.dt2解:回路磁通mBSBπr感应电动势大小dmd2dr(Bπr)B2πr0.40Vdtdtdt题7-2图7-2如题7-2图所示,载有电流I的长直导线附近,放一导体半圆环MeN与长直导线共面,且端点MN的连线与长直导线垂直.半圆环的半径为b,环心O与导线相距a.设半圆环以速度v平行导线平移.求半圆环内感应电动势的大小和方向及MN两端的电压UU.MN解:作辅助线MN,则在MeNM回路中,沿v方向运动时d0m∴0MeNM即MeNMNabIvab0又∵MNvBcosdlln0ab2ab所以沿NeM方向,MeNIvab0大小为ln2abM点电势高于N点电势,即0IvabUMUNln2ab题7-3图7-3如题7-3所示,在两平行载流的无限长直导线的平面内有一矩形线圈.两导线中的电流dI方向相反、大小相等,且电流以的变化率增大,求:dt(1)任一时刻线圈内所通过的磁通量;(2)线圈中的感应电动势.解:以向外磁通为正则baIdaIIlbada000(1)mldrldr[lnln]b2πrd2πr2πbddldabadI0(2)[lnln]dt2πdbdt7-4如题7-4图所示,长直导线通以电流I=5A,在其右方放一长方形线圈,两者共面.线
bav-1d圈长=0.06m,宽=0.04m,线圈以速度=0.03m·s:=0.05m时线圈中感应电动势的大小和方向.题7-4图解:AB、CD运动速度v方向与磁力线平行,不产生感应电动势.DA产生电动势AI01(vB)dlvBbvbD2dBC产生电动势CI0(vB)dlvb2B2π(ad)∴回路中总感应电动势0Ibv11812()1.610V2πdda方向沿顺时针.7-5长度为l的金属杆ab以速率v在导电轨道abcd上平行移动.已知导轨处于均匀磁场B中,B的方向与回路的法线成60°角(如题7-5图所示),B的大小为B=kt(k为正常).设t=0时杆位于cd处,求:任一时刻t导线回路中感应电动势的大小和方向.2112解:mBdSBlvtcos60ktlvklvt22dm∴klvtdt即沿abcd方向顺时针方向.题7-5图7-6一矩形导线框以恒定的加速度向右穿过一均匀磁场区,B的方向如题7-6图所示.取逆时针方向为电流正方向,画出线框中电流与时间的关系(设导线框刚进入磁场区时t=0).d解:如图逆时针为矩形导线框正向,则进入时0,0;dt题7-6图(a)题7-6图(b)d在磁场中时0,0;dt
d出场时0,0,故It曲线如题7-6图(b)所示.dt题7-7图l7-7一导线ab长为l,绕过O点的垂直轴以匀角速转动,aO=磁感应强度B平行于转3轴,如图10-10所示.试求:(1)ab两端的电势差;(2)a,b两端哪一点电势高?解:(1)在Ob上取rrdr一小段2l2B2则3rBdrlOb09l12同理3rBdrBlOa01812212∴abaOOb()BlBl1896(2)∵0即UU0abab∴b点电势高.题7-8图7-8一无限长的直导线和一正方形的线圈如题7-8图所示放置(导线与线圈接触处绝缘).求:线圈与导线间的互感系数.解:设长直电流为I,其磁场通过正方形线圈的互感磁通为2aIaIa30dr0ln212a2πr2π3a120∴Mln2I2π题7-9图7-9两根平行长直导线,横截面的半径都是a,中心相距为d,两导线属于同一回路.设两导线内部的磁通可忽略不计,证明:这样一对导线长度为l的一段自感为0ldaLIn.a解:如图7-9图所示,取dSldr
daIIIlda11Ildad0000则()ldr()dr(lnln)a2rπ2π(dr)2πarrd2πadaIlda0lnπalda0∴LlnIπa7-10两线圈顺串联后总自感为1.0H,在它们的形状和位置都不变的情况下,反串联后总自感为0.4H.试求:它们之间的互感.解:∵顺串时LL1L22M反串联时LL1L22M∴LL4MLLM0.15H47-11图7-11一矩形截面的螺绕环如题7-11图所示,共有N匝.试求:(1)此螺线环的自感系数;(2)若导线内通有电流I,环内磁能为多少?解:如题7-11图示(1)通过横截面的磁通为bNINIhb00hdrlna2rπ2πa20NIhb磁链Nln2πa20Nhb∴LlnI2πa12(2)∵WmLI2220NIhb∴Wmln4πa7-12一无限长圆柱形直导线,其截面各处的电流密度相等,总电流为I.求:导线内部单位长度上所储存的磁能.I0r解:在rR时B22πR222BIr0∴wm24208πR取dV2πrdr(∵导线长l1)232RRIrdrI00则W0wm2rdr044πR16π
7-13圆柱形电容器内、外导体截面半径分别为R1和R2(R1<R2),中间充满介电常数为dU的电介质.当两极板间的电压随时间的变化k时(k为常数),求介质内距圆柱轴线为dtr处的位移电流密度.2l解:圆柱形电容器电容CR2lnR12lUqCUR2lnR1q2lUUDSR2R22rlnrlnRR11Dk∴jtR2rlnR1dU7-14试证:平行板电容器的位移电流可写成IdC.式中C为电容器的电容,U是dt电容器两极板的电势差.如果不是平板电容器,以上关系还适用吗?解:∵qCUCUD0S∴DDSCUddUDICDdtdt不是平板电容器时D仍成立0dU∴IDC还适用.dt7-15半径为R=0.10m的两块圆板构成平行板电容器,放在真空中.今对电容器匀速充电,dE13-1-1使两极板间电场的变化率为=1.0×10V·m·s.求两极板间的位移电流,并计算电dt容器内离两圆板中心联线r(r<R)处的磁感应强度Br以及r=R处的磁感应强度BR.DE解:(1)jD0tt2IjSjR2.8ADDD(2)∵lHdlI0jDdSS取平行于极板,以两板中心联线为圆心的圆周l2r,则2dE2H2rjDr0rdtrdE∴H02dt
rdE00Br0H2dt00RdE6当rR时,BR5.610T2dt习题八328-1质量为1010kg的小球与轻弹簧组成的系统,按x0.1cos(8)(SI)的规律3作谐振动,求:(1)振动的周期、振幅和初位相及速度与加速度的最大值;(2)最大的回复力、振动能量、平均动能和平均势能,在哪些位置上动能与势能相等?(3)t25s与t11s两个时刻的位相差;解:(1)设谐振动的标准方程为xAcos(t),则知:021A0.1m,8,Ts,02/3411又vmA0.8ms2.51ms22amA63.2ms(2)Fmam0.63N122Emvm3.1610J212EpEkE1.5810J2当EkEp时,有E2Ep,12112即kx(kA)22222∴xAm220(3)(t2t1)8(51)328-2一个沿x轴作简谐振动的弹簧振子,振幅为A,周期为T,其振动方程用余弦函数表示.如果t0时质点的状态分别是:(1)xA;0(2)过平衡位置向正向运动;A(3)过x处向负向运动;2A(4)过x处向正向运动.2试求出相应的初位相,并写出振动方程.x0Acos0解:因为vAsin00将以上初值条件代入上式,使两式同时成立之值即为该条件下的初位相.故有
21xAcos(t)T3232xAcos(t)2T223xAcos(t)3T35254xAcos(t)4T438-3一质量为1010kg的物体作谐振动,振幅为24cm,周期为4.0s,当t0时位移为24cm.求:(1)t0.5s时,物体所在的位置及此时所受力的大小和方向;(2)由起始位置运动到x12cm处所需的最短时间;(3)在x12cm处物体的总能量.2解:由题已知A2410m,T4.0s21∴0.5radsT又,t0时,xA,000故振动方程为2x2410cos(0.5t)m(1)将t0.5s代入得2x0.52410cos(0.5t)m0.17m2Fmamx3231010()0.174.210N2方向指向坐标原点,即沿x轴负向.(2)由题知,t0时,0,0Att时x0,且v0,故t232∴t/s323(3)由于谐振动中能量守恒,故在任一位置处或任一时刻的系统的总能量均为12122EkAmA2213221010()(0.24)2247.110J8-4有一轻弹簧,下面悬挂质量为1.0g的物体时,伸长为4.9cm.用这个弹簧和一个质量为8.0g的小球构成弹簧振子,将小球由平衡位置向下拉开1.0cm后,给予向上的初速1度v05.0cms,求振动周期和振动表达式.3m1g1.0109.81解:由题知k0.2Nm2x4.910122-1而t0时,x01.010m,v05.010ms(设向上为正)
k0.22又5,即T1.26s3m8102v02Ax()02225.0102(1.010)()52210m2v05.0105tan1,即020x01.0105425∴x210cos(5t)m48-5图为两个谐振动的xt曲线,试分别写出其谐振动方程.题8-5图3解:由题8-5图(a),∵t0时,x00,v00,0,又,A10cm,T2s221即radsT3故xa0.1cos(t)m2A5由题8-5图(b)∵t0时,x0,v00,023t10时,x10,v10,12255又11325∴655故xb0.1cos(t)m638-6有两个同方向、同频率的简谐振动,其合成振动的振幅为0.20m,位相与第一振动的位相差为,已知第一振动的振幅为0.173m,求第二个振动的振幅以及第一、第二两振6动的位相差.
题8-6图解:由题意可做出旋转矢量图如下.由图知222AAA2AAcos3021122(0.173)(0.2)20.1730.23/20.01∴A20.1m设角AA1O为,则222AAA2AAcos1212222222A1A2A(0.173)(0.1)(0.02)cos即2AA20.1730.1120即,这说明,A1与A2间夹角为,即二振动的位相差为.2228-7试用最简单的方法求出下列两组谐振动合成后所得合振动的振幅:x5cos(3t)cmx5cos(3t)cm1313(1)(2)74x5cos(3t)cmx5cos(3t)cm22337解:(1)∵212,33∴合振幅AA1A210cm4(2)∵,33∴合振幅A08-8一质点同时参与两个在同一直线上的简谐振动,振动方程为x0.4cos(2t)m165x0.3cos(2t)m26试分别用旋转矢量法和振动合成法求合振动的振动幅和初相,并写出谐振方程。5解:∵()66∴A合A1A20.1m50.4sin0.3sinA1sin1A2sin2663tanAcosAcos5321220.4cos0.3cos66
∴6其振动方程为x0.1cos(2t)m6(作图法略)习题九9-1振动和波动有什么区别和联系?平面简谐波动方程和简谐振动方程有什么不同?又有什么联系?振动曲线和波形曲线有什么不同?解:(1)振动是指一个孤立的系统(也可是介质中的一个质元)在某固定平衡位置附近所做yf(t)的往复运动,系统离开平衡位置的位移是时间的周期性函数,即可表示为;波动是振动在连续介质中的传播过程,此时介质中所有质元都在各自的平衡位置附近作振动,因xtyf(x,t)此介质中任一质元离开平衡位置的位移既是坐标位置,又是时间的函数,即.yf(t)t(2)在谐振动方程中只有一个独立的变量时间,它描述的是介质中一个质元偏离yf(x,t)平衡位置的位移随时间变化的规律;平面谐波方程中有两个独立变量,即坐标位置x和时间t,它描述的是介质中所有质元偏离平衡位置的位移随坐标和时间变化的规律.xyAcos(t)当谐波方程u中的坐标位置给定后,即可得到该点的振动方程,而波源持续不断地振动又是产生波动的必要条件之一.yf(t)y(3)振动曲线描述的是一个质点的位移随时间变化的规律,因此,其纵轴为,横轴为t;波动曲线yf(x,t)描述的是介质中所有质元的位移随位置,随时间变化的规律,yxx其纵轴为,横轴为.每一幅图只能给出某一时刻质元的位移随坐标位置变化的规律,即只能给出某一时刻的波形图,不同时刻的波动曲线就是不同时刻的波形图.xxtyAu0uyA9-2波动方程=cos[()+]中的表示什么?如果改写为=cosxxxtt0(u),u又是什么意思?如果t和x均增加,但相应的[(u)+0]的值不变,由此能从波动方程说明什么?xx/uxu解:波动方程中的表示了介质中坐标位置为的质元的振动落后于原点的时间;xt则表示处质元比原点落后的振动位相;设时刻的波动方程为xyAcos(t)t0utt则时刻的波动方程为(xx)yAcos[(tt)]tt0ux(t)其表示在时刻t,位置x处的振动状态,经过t后传播到xut处.所以在u中,x(t)当t,x均增加时,u的值不会变化,而这正好说明了经过时间t,波形即向前传
xyAcos(t)0播了xut的距离,说明u描述的是一列行进中的波,故谓之行波方程.9-3在驻波的两相邻波节间的同一半波长上,描述各质点振动的什么物理量不同,什么物理量相同?2y2Acosxcosvt解:取驻波方程为,则可知,在相邻两波节中的同一半波长上,描述各质点的振幅是不相同的,各质点的振幅是随位置按余弦规律变化的,即振幅变化规律22Acosx可表示为.而在这同一半波长上,各质点的振动位相则是相同的,即以相邻两波节的介质为一段,同一段介质内各质点都有相同的振动位相,而相邻两段介质内的质点振动位相则相反.yABtCxAB9-4已知波源在原点的一列平面简谐波,波动方程为=cos(),其中,,C为正值恒量.求:(1)波的振幅、波速、频率、周期与波长;l(2)写出传播方向上距离波源为处一点的振动方程;d(3)任一时刻,在波的传播方向上相距为的两点的位相差.解:(1)已知平面简谐波的波动方程yAcos(BtCx)x0()将上式与波动方程的标准形式xyAcos(2t2)比较,可知:B波振幅为A,频率2,2Bu波长C,波速C,12T波动周期B.xl(2)将代入波动方程即可得到该点的振动方程yAcos(BtCl)(3)因任一时刻t同一波线上两点之间的位相差为2(xx)212xxd将21,及C代入上式,即得Cd.yt4xxy9-5沿绳子传播的平面简谐波的波动方程为=0.05cos(10),式中,以米计,t以秒计.求:(1)波的波速、频率和波长;(2)绳子上各质点振动时的最大速度和最大加速度;xt(3)求=0.2m=1s时的位相,它是原点在哪一时刻的位相?这一位相所代表的
运动状态在t=1.25s时刻到达哪一点?解:(1)将题给方程与标准式2yAcos(2tx)11相比,得振幅A0.05m,频率5s,波长0.5m,波速u2.5ms.(2)绳上各点的最大振速,最大加速度分别为vA100.050.5ms1max222aA(10)0.0552maxmsx0.2(3)m处的振动比原点落后的时间为x0.20.08u2.5sx0.2mt1sx0t010.080.92s故,时的位相就是原点(),在时的位相,9.2即π.t1.25x设这一位相所代表的运动状态在s时刻到达点,则xxu(tt)0.22.5(1.251.0)0.825m11-3-2-19-6一平面余弦波,沿直径为14cm的圆柱形管传播,波的强度为18.0×10J·m·s,频-1率为300Hz,波速为300m·s,求:(1)波的平均能量密度和最大能量密度?(2)两个相邻同相面之间有多少波的能量?Iwu解:(1)∵3I105w18.06103∴u300Jm4w2w1.2103maxJm1212uWVwdwd(2)445123007610(0.14)9.24104300JSSA4SS29-71和2为两相干波源,振幅均为1,相距,1较2位相超前,求:S(1)1外侧各点的合振幅和强度;S(2)2外侧各点的合振幅和强度SSrSSP解:(1)在1外侧,距离1为1的点,12传到该点引起的位相差为2r(r)21142AAA0,IA011SSrSS(2)在2外侧.距离2为1的点,12传到该点引起的位相差.2(rr)0222422AAA2A,IA4A11119-8如题9-8图所示,设B点发出的平面横波沿BP方向传播,它在B点的振动方程为
3y210cos2tCCPC1;点发出的平面横波沿方向传播,它在点的振动方程为3y210cos(2t)ytBPCP2,本题中以m计,以s计.设=0.4m,=0.5m,u-1波速=0.2m·s,求:(1)两波传到P点时的位相差;(2)当这两列波的振动方向相同时,P处合振动的振幅;*(3)当这两列波的振动方向互相垂直时,P处合振动的振幅.2()(CPBP)21解:(1)(CPBP)u2(0.50.4)00.2题9-8图(2)P点是相长干涉,且振动方向相同,所以3AAA410P12m0(3)若两振动方向垂直,又两分振动位相差为,这时合振动轨迹是通过Ⅱ,Ⅳ象限的直线,所以合振幅为2233AAA2A22102.8310121myxt9-9一驻波方程为=0.02cos20cos750(SI),求:(1)形成此驻波的两列行波的振幅和波速;(2)相邻两波节间距离.解:(1)取驻波方程为2xy2Acoscos2tu0.02A0.01故知2m7502202750,则2,u22750/2u37.51∴2020msu2/200.10.314(2)∵m所以相邻两波节间距离x0.1572mytx9-10在弦上传播的横波,它的波动方程为1=0.1cos(13+0.0079)(SI)x试写出一个波动方程,使它表示的波能与这列已知的横波叠加形成驻波,并在=0处为波节.x0x0解:为使合成驻波在处形成波节,则要反射波在处与入射波有的位相差,故
反射波的波动方程为y0.1cos(13t0.0079x)29-11汽车驶过车站时,车站上的观测者测得汽笛声频率由1200Hz变到了1000Hz,设空气-1中声速为330m·s,求汽车的速率.v解:设汽车的速度为s,汽车在驶近车站时,车站收到的频率为u10uvsu20uv汽车驶离车站时,车站收到的频率为s联立以上两式,得1200100012u3003011200100ms112-1-19-12两列火车分别以72km·h和54km·h的速度相向而行,第一列火车发出一个600Hz-1的汽笛声,若声速为340m·s,求第二列火车上的观测者听见该声音的频率在相遇前和相遇后分别是多少?v20ms1v215ms1解:设鸣笛火车的车速为1,接收鸣笛的火车车速为,则两者相遇前收到的频率为uv34015260066510uv340201Hz两车相遇之后收到的频率为uv34015260054110uv340201Hz习题十10-1在杨氏双缝实验中,作如下调节时,屏幕上的干涉条纹将如何变化?试说明理由.(1)使两缝之间的距离变小;(2)保持双缝间距不变,使双缝与屏幕间的距离变小;(3)整个装置的结构不变,全部浸入水中;(4)光源作平行于S1,S2联线方向上下微小移动;(5)用一块透明的薄云母片盖住下面的一条缝.D解:由x知,(1)条纹变疏;(2)条纹变密;(3)条纹变密;(4)零级明纹在屏幕上作d相反方向的上下移动;(5)零级明纹向下移动.10-2什么是光程?在不同的均匀媒质中,若单色光通过的光程相等时,其几何路程是否相2同?其所需时间是否相同?在光程差与位相差的关系式中,光波的波长要用真空中波长,为什么?解:nr.不同媒质若光程相等,则其几何路程定不相同;其所需时间相同,为t.C因为中已经将光在介质中的路程折算为光在真空中所走的路程。10-3用劈尖干涉来检测工件表面的平整度,当波长为的单色光垂直入射时,观察到的干涉条纹如题12-5图所示,每一条纹的弯曲部分的顶点恰与左邻的直线部分的连线相切.试说明工件缺陷是凸还是凹?并估算该缺陷的程度.
解:工件缺陷是凹的.故各级等厚线(在缺陷附近的)向棱边方向弯曲.按题意,每一条纹弯曲部分的顶点恰与左邻的直线部分连线相切,说明弯曲部分相当于条纹向棱边移动了一条,故相应的空气隙厚度差为e,这也是工件缺陷的程度.2题10-3图10-4在杨氏双缝实验中,双缝间距d=0.20mm,缝屏间距D=1.0m,试求:(1)若第二级明条纹离屏中心的距离为6.0mm,计算此单色光的波长;(2)相邻两明条纹间的距离.3D110解:(1)由x明k知,6.02,d0.2o3∴0.610mm6000A3D1103(2)x0.6103mmd0.210-5在双缝装置中,用一很薄的云母片(n=1.58)覆盖其中的一条缝,结果使屏幕上的第七o级明条纹恰好移到屏幕中央原零级明纹的位置.若入射光的波长为5500A,求此云母片的厚度.解:设云母片厚度为e,则由云母片引起的光程差为nee(n1)e按题意710775500106∴e6.610m6.6mn11.581o10-6白光垂直照射到空气中一厚度为3800A的肥皂膜上,设肥皂膜的折射率为1.33,试问该膜的正面呈现什么颜色?背面呈现什么颜色?解:由反射干涉相长公式有2nek(k1,2,)24ne41.33380020216得2k12k12k1ok2,26739A(红色)ok3,4043A(紫色)3所以肥皂膜正面呈现紫红色.由透射干涉相长公式2nek(k1,2,)2ne10108所以kko当k2时,=5054A(绿色)故背面呈现绿色.
10-7在折射率n1=1.52的镜头表面涂有一层折射率n2=1.38的MgF2增透膜,如果此膜适o用于波长=5500A的光,问膜的厚度应取何值?解:设光垂直入射增透膜,欲透射增强,则膜上、下两表面反射光应满足干涉相消条件,即12n2e(k)(k0,1,2,)21(k)2k∴e2n2n4n22255005500ok(1993k996)A21.3841.38o令k0,得膜的最薄厚度为996A.当k为其他整数倍时,也都满足要求.10-8当牛顿环装置中的透镜与玻璃之间的空间充以液体时,第十个亮环的直径由d1=1.40-2d-2×10m变为2=1.27×10m,求液体的折射率.解:由牛顿环明环公式D1(2k1)Rr空22D2(2k1)Rr液22n2D1D11.96两式相除得n,即n1.222D2D21.6110-9利用迈克耳逊干涉仪可测量单色光的波长.当M1移动距离为0.322mm涉条纹移动数为1024条,求所用单色光的波长.解:由dN23d0.32210得22N1024o76.28910m6289A10-10什么叫半波带?单缝衍射中怎样划分半波带?对应于单缝衍射第3级明条纹和第4级暗条纹,单缝处波面各可分成几个半波带?答:半波带由单缝A、B首尾两点向方向发出的衍射线的光程差用来划分.对应于第23级明纹和第4级暗纹,单缝处波面可分成7个和8个半波带.∵由asin(2k1)(231)7222asin48210-11若以白光垂直入射光栅,不同波长的光将会有不同的衍射角.问(1)零级明条纹能否分开不同波长的光?(2)在可见光中哪种颜色的光衍射角最大?不同波长的光分开程度与什么因素有关?解:(1)零级明纹不会分开不同波长的光.因为各种波长的光在零级明纹处均各自相干加强.
(2)可见光中红光的衍射角最大,因为由(ab)sink,对同一k值,衍射角.ο10-12一单色平行光垂直照射一单缝,若其第三级明条纹位置正好与6000A的单色平行光的第二级明条纹位置重合,求前一种单色光的波长.解:单缝衍射的明纹公式为asin(2k1)2o当6000A时,k2时,k3x重合时角相同,所以有6000asin(221)(231)x225o得x60004286A710-13用橙黄色的平行光垂直照射一宽为a=0.60mm的单缝,缝后凸透镜的焦距f=40.0cm,观察屏幕上形成的衍射条纹.若屏上离中央明条纹中心1.40mm处的P点为一明条纹;求:(1)入射光的波长;(2)P点处条纹的级数;(3)从P点看,对该光波而言,狭缝处的波面可分成几个半波带?解:(1)由于P点是明纹,故有asin(2k1),k1,2,32x1.43由3.510tansinf4002asin20.63故3.5102k12k1134.210mm2k1o当k3,得6000A3ok4,得44700Ao(2)若6000A,则P点是第3级明纹;3o若44700A,则P点是第4级明纹.(3)由asin(2k1)可知,2当k3时,单缝处的波面可分成2k17个半波带;当k4时,单缝处的波面可分成2k19个半波带.o10-14用5900A的钠黄光垂直入射到每毫米有500条刻痕的光栅上,问最多能看到第几级明条纹?1o34解:abmm2.010mm2.010A500由(ab)sink知,最多见到的条纹级数kmax对应的,24ab2.010所以有k3.39,即实际见到的最高级次为k3.maxmax5900
o10-15波长6000A的单色光垂直入射到一光栅上,第二、第三级明条纹分别出现在sin0.20与sin0.30处,第四级缺级.求:(1)光栅常数;(2)光栅上狭缝的宽度;(3)在90°>>-90°范围内,实际呈现的全部级数.解:(1)由(ab)sink式对应于sin10.20与sin20.30处满足:100.20(ab)2600010100.30(ab)36000106得ab6.010m(2)因第四级缺级,故此须同时满足(ab)sinkasinkab6解得ak1.510k46取k1,得光栅狭缝的最小宽度为1.510m(3)由(ab)sink(ab)sink当,对应kkmax26ab6.010∴k10max10600010因4,8缺级,所以在9090范围内实际呈现的全部级数为k0,1,2,3,5,6,7,9共15条明条纹(k10在k90处看不到).10-16使自然光通过两个偏振化方向夹角为60°的偏振片时,透射光强为I1,今在这两个偏振片之间再插入一偏振片,它的偏振化方向与前两个偏振片均成30°,问此时透射光I与I1之比为多少?解:由马吕斯定律I02οI0I1cos6028I9I02ο2ο0Icos30cos30232I9∴2.25I4110-17一束自然光从空气入射到折射率为1.40的液体表面上,其反射光是完全偏振光.试求:(1)入射角等于多少?(2)折射角为多少?1.40ο"解:(1)tani0,∴i054281οο"(2)y90i0353210-18利用布儒斯特定律怎样测定不透明介质的折射率?若测得釉质在空气中的起偏振角为58°,求釉质的折射率.οn解:由tan58,故n1.601
习题十一l11-1设图11-1中车厢上观测者测得前后门距离为2.试用洛仑兹变换计算地面上的观测者测到同一光信号到达前、后门的时间差.l(x,t)(l,)11(S)解:设光讯号到达前门为事件1,在车厢(S)系时空坐标为c,在车站系:ululut(tx)(l)(1)11212cccccl(x,t)(l,)22(S)光信号到达后门为事件2,则在车厢(S)系坐标为c,在车站系:ulut(tx)(1)2222ccclutt2212于是ct0,ttt,xxx2l或者1212uut(tx)(2l)22ccSx11-2惯性系S′相对另一惯性系沿轴作匀速直线运动,取两坐标原点重合时刻作为计时起点.在S系中测得两事件的时空坐标分别为x1=6×104m,t1=2×10-4s,以及x2=12×104m,t2-4=1×10s.已知在S′系中测得该两事件同时发生.试问:(1)S′系相对S系的速度是多S少?(2)系中测得的两事件的空间间隔是多少?(S)Sv解:设相对的速度为,vt(tx)1121(1)cvt(tx)2222ctt0由题意21vtt(xx)21221则c2t2t1c8vc1.510xx2ms1故21x(xvt),x(xvt)(2)由洛仑兹变换1112224xx5.210m代入数值,21l0x′"x11-3长度=1mS′系中,与轴的夹角=30°,S′系相对S系沿轴x运动,在S系中观测者测得米尺与轴夹角为45.试求:(1)S′系和S系的相对运动速度.(2)S系中测得的米尺长度.Sx,y解:(1)米尺相对静止,它在轴上的投影分别为:
LxL0cos0.866m,LyL0sin0.5mSxvSxy米尺相对沿方向运动,设速度为,对系中的观察者测得米尺在方向收缩,而方向的长度不变,即2vLL1,LLxx2yycLLLyyytanLLv2xxL1x2c故45οL,L把及xy代入2v0.512则得c0.866v0.816c故LyL0.707m(2)在S系中测得米尺长度为sin45题11-4图OO11-4两个惯性系中的观察者和以0.6c(c表示真空中光速)的相对速度相互接近,如果OO测得两者的初始距离是20m,则测得两者经过多少时间相遇?Ot解:测得相遇时间为L200tv0.6cOt测得的是固有时2tL01tv∴88.8910s,v0.6c,10.8,O或者,测得长度收缩,22LLL1L10.60.8L,t000v0.8L00.8208t8.8910s80.6c0.6310SS11-5观测者甲乙分别静止于两个惯性参考系和中,甲测得在同一地点发生的两事件的时间间隔为4s,而乙测得这两个事件的时间间隔为5s.求:SS(1)相对于的运动速度.
(2)乙测得这两个事件发生的地点间的距离.t4s,x0t5sxxx解:甲测得,乙测得,坐标差为21′v1t(tx)tt2cv21()c(1)∴2vt412ct5t2423vc1()c1()ct55解出811.810mst5xxvt,,x0(2)t4538xvtc43c910m∴45xx0负号表示21.11-6一宇航员要到离地球为5光年的星球去旅行.如果宇航员希望把这路程缩短为3光年,则他所乘的火箭相对于地球的速度是多少?2232l3l151,则10解:594v1cc255∴11-7论证以下结论:在某个惯性系中有两个事件同时发生在不同地点,在有相对运动的其他惯性系中,这两个事件一定不同时.SA、Ba,bxxbxa,ttAtBS证:设在系事件在处同时发生,则,在系中测得vttt(tx)BA2ct0,x0,t0∴即不同时发生.11-8试证明:(1)如果两个事件在某惯性系中是同一地点发生的,则对一切惯性系来说这两个事件的时间间隔,只有在此惯性系中最短.(2)如果两个事件在某惯性系中是同时发生的,则对一切惯性关系来说这两个事件的空间间隔,只有在此惯性系中最短.SA、Bx0S解:(1)如果在系中,两事件在同一地点发生,则,在系中,tttv0t,仅当时,等式成立,∴最短.St0Sxxxv0(2)若在系中同时发生,即,则在系中,,仅当时等式Sx成立,∴系中最短.v11-96000m的高空大气层中产生了一个介子以速度=0.998c飞向地球.假定该介子-6在其自身静止系中的寿命等于其平均寿命2×10s.试分别从下面两个角度,即地球上的观
测者和介子静止系中观测者来判断介子能否到达地球.6t0210s解:介子在其自身静止系中的寿命是固有(本征)时间,对地球观测者,由于时间膨胀效应,其寿命延长了.衰变前经历的时间为t05t3.1610s2v12cdvt9470m这段时间飞行距离为d6000m因,故该介子能到达地球.vt0或在介子静止系中,介子是静止的.地球则以速度接近介子,在时间内,地球接dvt599m近的距离为0d6000m0经洛仑兹收缩后的值为:2vdd1379m002cdd0,故介子能到达地球.x11-10设物体相对S′系沿轴正向以0.8c运动,如果S′系相对S系沿x轴正向的速度也是0.8c,问物体相对S系的速度是多少?u0.8cvx0.8c解:根据速度合成定理,,vxu0.8c0.8cv0.98cxuv0.8c0.8cx1122∴cc11-11(1)火箭A和B分别以0.8c和0.6c的速度相对地球向+x和-x方向飞行.试求由火箭B测得A的速度.(2)若火箭A相对地球以0.8c的速度向+y方向运动,火箭B的速度不变,求A相对B的速度.aSBSSSu0.6cA解:(1)如图,取地球为系,为系,则相对的速度,火箭相对Svx0.8cASB的速度,则相对()的速度为:vxu0.8c(0.6c)v0.946cxu(0.6c)(0.8c)1v12x2cc或者取A为S系,则u0.8c,B相对S系的速度vx0.6c,于是B相对A的速度为:vxu0.6c0.8cv0.946cxu(0.8c)(0.6c)1v12x2ccbSBSSSx(2)如图,取地球为系,火箭为系,系相对系沿方向运动,速度u0.6cASvx0vy0.8cAB,对系的速度为,,,由洛仑兹变换式相对的速度为:vxu0(0.6c)v0.6cxu101v2xc
2u1v2yc2v10.6(0.8c)0.64cyu1v2xc∴A相对B的速度大小为22vvv0.88cxyx速度与轴的夹角为vytan1.07vxο46.8题11-11图11-12(1)如果将电子由静止加速到速率为0.1c,须对它作多少功?(2)如果将电子由速率为0.8c加速到0.9c,又须对它作多少功?解:(1)对电子作的功,等于电子动能的增量,得22221EEmcmcmc(1)mc(1)kk0002v12c318219.110(310)(1)210.11634.12102.5710eVJ=2222EEE(mcmc)(mcmc)kkk2010(2)2122211mcmcmc()21022vv211122cc)31216119.110310()2210.910.81455.1410J3.2110eV0-611-12子静止质量是电子静止质量的207倍,静止时的平均寿命=2×10s,若它在实-6验室参考系中的平均寿命=7×10s,试问其质量是电子静止质量的多少倍?mvcm解:设子静止质量为0,相对实验室参考系的速度为,相应质量为,电子静017,即12122m0止质量为0e,因由质速关系,在实验室参考系中质量为:
m207m00em2211m2077207725122m0e故习题十二12-1将星球看做绝对黑体,利用维恩位移定律测量m便可求得T.这是测量星球表面温度的方法之一.设测得:太阳的m0.55m,北极星的m0.35m,天狼星的m0.29m,试求这些星球的表面温度.解:将这些星球看成绝对黑体,则按维恩位移定律:3mTb,b2.89710mK3b2.897103对太阳:T165.310Km0.551013b2.897103对北极星:T268.310Km0.351023b2.897104对天狼星:T361.010Km0.29103-212-2用辐射高温计测得炉壁小孔的辐射出射度(总辐射本领)为22.8W·cm,求炉内温度.解:炉壁小孔视为绝对黑体,其辐出度242M(T)22.8Wcm22.810WmB按斯特藩-玻尔兹曼定律:4MB(T)T41MB(T)22.8104T4()85.671022.8133()4101.4210K5.67ο12-3从铝中移出一个电子需要4.2eV的能量,今有波长为2000A的光投射到铝表面.试问:(1)由此发射出来的光电子的最大动能是多少?(2)遏止电势差为多大?(3)铝的截止(红限)波长有多大?解:(1)已知逸出功A4.2eV12据光电效应公式hvmvmA2则光电子最大动能:12hcEkmaxmvmhAA23486.6310310194.21.61010200010193.2310J2.0eV
12(2)eUaEkmaxmvm2193.2310∴遏止电势差U2.0Va191.610c(3)红限频率0,∴h0A,又00348hc6.6310310∴截止波长019A4.21.601072.9610m0.296m-712-4在一定条件下,人眼视网膜能够对5个蓝绿光光子(5.010m)产生光的感觉.此时视网膜上接收到光的能量为多少?如果每秒钟都能吸收5个这样的光子,则到达眼睛的功率为多大?解:5个兰绿光子的能量hcEnhn34856.631031075.010181.9910JE18功率1.9910Wt12-5若一个光子的能量等于一个电子的静能,试求该光子的频率、波长、动量.3134解:电子的静止质量m09.1110kg,h6.6310JS2当hm0c时,则23182m0c9.1110(310)34h6.6310201.23610Hzcο122.427110m0.02Ah221p2.7310kgms或Ecp2Em0c318221pmc9.11103102.7310kgms0cc12-6光电效应和康普顿效应都包含了电子和光子的相互作用,试问这两个过程有什么不同?答:光电效应是指金属中的电子吸收了光子的全部能量而逸出金属表面,是电子处于原子中束缚态时所发生的现象.遵守能量守恒定律.而康普顿效应则是光子与自由电子(或准自由电子)的弹性碰撞,同时遵守能量与动量守恒定律.12-7在康普顿效应的实验中,若散射光波长是入射光波长的1.2倍,则散射光子的能量ε与反冲电子的动能Ek之比ε/Ek等于多少?22解:由hv0m0chmc22Ekmcm0ch0hh(0)h
h∴5Eh()k000已知1.2由c1.20111则51.21.210.200οπ12-8波长00.708A的X射线在石腊上受到康普顿散射,求在和π方向上所散射的X2射线波长各是多大?解:在方向上:22h2Δsin0mc203426.6310sin3189.11103104ο122.4310m0.0243Aο散射波长0Δ0.7080.02480.732A在方向上2h22h12οΔ0sin4.8610m0.0486Amc2mc00ο散射波长0Δ0.7080.04860.756A12-9实验发现基态氢原子可吸收能量为12.75eV的光子.(1)试问氢原子吸收光子后将被激发到哪个能级?(2)受激发的氢原子向低能级跃迁时,可发出哪几条谱线?请将这些跃迁画在能级图上.13.6eV解:(1)13.6eV12.75eV0.85eV2n解得n411或者ERhc()221n1136.(1)12.752n解出n4题12-9图(2)可发出谱线赖曼系3条,巴尔末系2条,帕邢系1条,共计6条.12-10处于基态的氢原子被外来单色光激发后发出巴尔末线系中只有两条谱线,试求这两
条谱线的波长及外来光的频率.解:巴尔末系是由n2的高能级跃迁到n2的能级发出的谱线.只有二条谱线说明激发后最高能级是n4的激发态.E413.620.85eV4E313.621.51eV3E213.623.4eV2hchEEnmhcEEnmhcaEE323486.6310331019(3.41.51)1.6010ο10657310m6573Ahc6.6310343108ο4872A19EE(3.40.85)1.61042基态氢原子吸收一个光子h被激发到n4的能态hc∴hE4E119E4E1(13.60.85)1.610153.0810Hz34h6.6261012-11当基态氢原子被12.09eV的光子激发后,其电子的轨道半径将增加多少倍?1解:EnE113.6[12]12.09eVn13.613.612.092n213.613.6n,n3136.12.091.5122rnnr1,n9,rn9r1轨道半径增加到9倍.12-12德布罗意波的波函数与经典波的波函数的本质区别是什么?答:德布罗意波是概率波,波函数不表示实在的物理量在空间的波动,其振幅无实在的物理2意义,仅表示粒子某时刻在空间的概率密度.ο12-13为使电子的德布罗意波长为1A,需要多大的加速电压?12.25oo解:A1AU12.25u∴加速电压U150伏ο12-14光子与电子的波长都是2.0A,它们的动量和总能量各为多少?
2h解:由德布罗意关系:Emc,pmv波长相同它们的动量相等.34h6.631024-1p3.310kgms102.010光子的能量hc248163hpc3.3103109.910J6.210eV2223电子的总能量E(cp)(m0c),cp6.210eV26而m0c0.51MeV0.5110eV2∴m0ccp2222∴E(cp)(m0c)m0c0.51MeV12-15一个质量为m的粒子,约束在长度为L的一维线段上.试根据测不准关系估算这个粒子所具有的最小能量的值.解:按测不准关系,xph,pmv,则xxxhmxvxh,vxmx这粒子最小动能应满足22121h2hhEm(v)m()minx2222mx2mx2mLο12-16一波长为3000A的光子,假定其波长的测量精度为百万分之一,求该光子位置的测不准量.hhh解:光子p,p22由测不准关系,光子位置的不准确量为h23000o9x310A30cm6p1012-17波函数在空间各点的振幅同时增大D倍,则粒子在空间分布的概率会发生什么变化?解:不变.因为波函数是计算粒子t时刻空间各点出现概率的数学量.概率是相对值.则1、2点的概率比值为:22D1122D22∴概率分布不变.12-18已知粒子在一维矩形无限深势阱中运动,其波函数为:13x(x)cos(axa)a2a5那么,粒子在xa处出现的概率密度为多少?6*213x2解:(cos)a2a
53a126125coscosa2aa41212cos()cosa4a41121()a22a12-19粒子在一维无限深势阱中运动,其波函数为:2nxn(x)sin()(0xa)aa1若粒子处于n1的状态,在0~a区间发现粒子的概率是多少?4222x解:dwdxsindxaaa∴在0~区间发现粒子的概率为:4aa2xa2ax44242p0dw0sindx0sind(x)aaaaa2a/41x[1cos2]d(x)0.09102aan12-20宽度为a的一维无限深势阱中粒子的波函数为(x)Asinx,求:(1)归一化a系数A;(2)在n2时何处发现粒子的概率最大?2a2解:(1)归一化系数dxdx10a22na2ann即AsinxdxAsinxd(x)0an0aaa2a2nnA(1cosx)d(x)2n0aaa2a2AnA12n22∴Aa2n粒子的波函数(x)sinxaa22(2)当n2时,2sinxaa222214几率密度w2sinx[1cosx]aaaadw444令0,即sinx0,即sinx0,,dxaaa4xk,k0,1,2,a
a∴xk4又因0xa,k4,a3∴当x和xa时w有极大值,44a当x时,w0.2a3∴极大值的地方为,a处4412-21原子内电子的量子态由n,l,m,m四个量子数表征.当n,l,m一定时,不同的量子lsl态数目是多少?当n,l一定时,不同的量子态数目是多少?当n一定时,不同的量子态数目是多少?1解:(1)2(ms)21(2)2(2l1),每个l有2l1个ml,每个ml可容纳ms的2个量子态.22(3)2n12-22求出能够占据一个d分壳层的最大电子数,并写出这些电子的m,m值.ls解:d分壳层的量子数l2,可容纳最大电子数为Z2(2l1)2(221)10个,l这些电子的:m0,1,2,l1ms2'
您可能关注的文档
- 大学毛概课后习题及其准确答案.doc
- 大学物理(上)练习题解答.doc
- 大学物理(第五版)习题解答12-15 wan改正.doc
- 大学物理八九章部分习题解答.doc
- 大学物理学北邮第四版第一到六章课后题答案.doc
- 大学物理学答案上册.doc
- 大学物理知识总结习题答案(第四章)静电场.doc
- 大学物理答案(上).doc
- 大学物理答案第十六章.doc
- 大学物理简明教程课后习题加答案《完整版》.doc
- 大学物理课后习题答案(上).docx
- 大学物理课后习题答案(下).docx
- 大学物理课后习题答案.doc
- 大学物理课后答案9-10.doc
- 大学物理题库参考答案力学.doc
- 大学生_必备资料下载.doc
- 大学生信息检索习题以及答案 (2).doc
- 大学生信息检索习题以及答案.doc