- 583.89 KB
- 2022-04-29 14:12:41 发布
- 1、本文档共5页,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,可选择认领,认领后既往收益都归您。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细先通过免费阅读内容等途径辨别内容交易风险。如存在严重挂羊头卖狗肉之情形,可联系本站下载客服投诉处理。
- 文档侵权举报电话:19940600175。
'第12章机械振动习题及答案1、什么是简谐振动?哪个或哪几个是表示质点作简谐振动时加速度和位移关系的?(1);(2);(3);(4).答:系统在线性回复力的作用下,作周期性往复运动,即为简谐振动。对于简谐振动,有,故(3)表示简谐振动。2、对于给定的弹簧振子,当其振幅减为原来的1/2时,下列哪些物理量发生了变化?变化为原来的多少倍?(1)劲度系数;(2)频率;(3)总机械能;(4)最大速度;(5)最大加速度。解:当时,(1)劲度系数k不变。(2)频率不变。(3)总机械能(4)最大速度(5)最大加速度3、劲度系数为k和k的两根弹簧,与质量为m的小球按题图所示的两种方式连接,试证明它们的振12动均为谐振动,并分别求出它们的振动周期.解:(1)图(a)中为串联弹簧,对于轻弹簧在任一时刻应有FFF,设串联弹簧的等效倔强系数为12Fkx串K等效位移为x,则有串Fkx1111
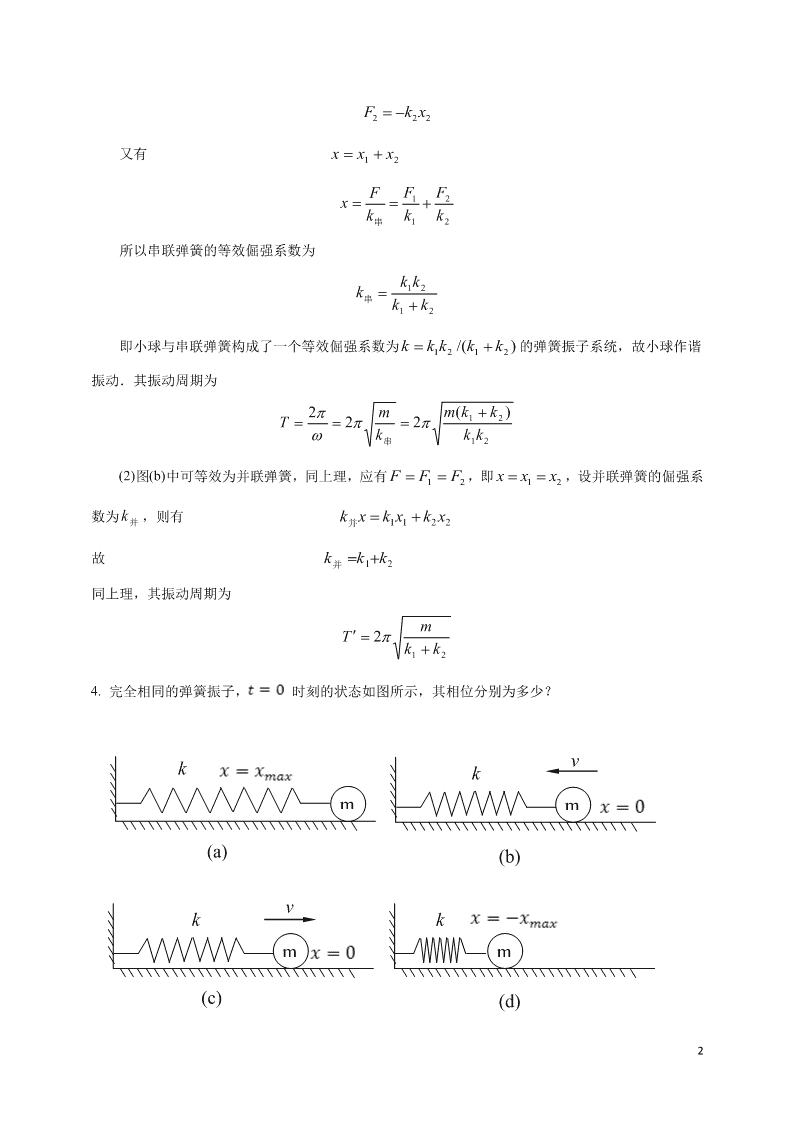
Fkx222又有xxx12FFF12xkkk串12所以串联弹簧的等效倔强系数为kk12k串kk12即小球与串联弹簧构成了一个等效倔强系数为kkk/(kk)的弹簧振子系统,故小球作谐1212振动.其振动周期为2mm(k1k2)T22kkk串12(2)图(b)中可等效为并联弹簧,同上理,应有FFF,即xxx,设并联弹簧的倔强系1212数为k,则有kxkxkx并并1122故kkk并12同上理,其振动周期为mT2kk124.完全相同的弹簧振子,时刻的状态如图所示,其相位分别为多少?vkkmm(a)(b)vkkmm(c)(d)2
解:对于弹簧振子,时,,(a),故,故(b),故,故(c),故,故(d),故,故5、如图所示,物体的质量为m,放在光滑斜面上,斜面与水平面的夹角为,弹簧的倔强系数为k,滑轮的转动惯量为I,半径为R。先把物体托住,使弹簧维持原长,然后由静止释放,试证明物体作简谐振动,并求振动周期.解:分别以物体m和滑轮为对象,其受力如题图(b)所示,以重物在斜面上静平衡时位置为坐标原点,沿斜面向下为x轴正向,则当重物偏离原点的坐标为x时,有2dxmgsinTm①12dtTRTRI②122dxRTk(xx)③220dt式中xmgsin/k,为静平衡时弹簧之伸长量,联立以上三式,有02Idx(mR)kxR2Rdt3
22kR令2mRI则有2dx2x02dt故知该系统是作简谐振动,其振动周期为222mRImI/RT2(2)2kRK326、质量为1010kg的小球与轻弹簧组成的系统,按x0.1cos(8)(SI)的规律作谐振动,3求:(1)振动的周期、振幅和初位相及速度与加速度的最大值;(2)最大的回复力、振动能量,在哪些位置上动能与势能相等?解:(1)设谐振动的标准方程为xAcos(t),则知:021A0.1m,8,Ts,2/30411又vA0.8ms2.51msm22aA63.2msm(2)Fma0.63Nmm122Emv3.1610Jm2当EE时,有E2E,kpp12112即kx(kA)22222∴xAm2207、一个沿x轴作简谐振动的弹簧振子,振幅为A,周期为T,其振动方程用余弦函数表示.如果t0时质点的状态分别是:(1)xA;0(2)过平衡位置向正向运动;A(3)过x处向负向运动;24
A(4)过x处向正向运动.2试求出相应的初位相,并写出振动方程.x0Acos0解:因为vAsin00将以上初值条件代入上式,使两式同时成立之值即为该条件下的初位相.故有2xAcos(t)1T323xAcos(t)22T22xAcos(t)33T3525xAcos(t)44T48.物体沿x轴作简谐振动,在时刻,其坐标为,速度,加速度,试求:(1)弹簧振子的角频率和周期;(2)初相位和振幅。解:设,则时(1)(2)222v020.0092Ax0.0858.5cm02223.50v00.0092tan0.00461x23.5(0.085)005
095.19、两质点作同方向、同频率的简谐振动,振幅相等。当质点1在处,且向左运动时,另一个质点2在处,且向右运动。求这两个质点的相位差。解:由旋转矢量图可知,当质点1在处,且向左运动时,相位为;而质点2在处,且向右运动,相位为(如图)。所以他们的相位差为。310、一质量为1010kg的物体作谐振动,振幅为24cm,周期为4.0s,当t0时位移为24cm.求:(1)t0.5s时,物体所在的位置及此时所受力的大小和方向;(2)由起始位置运动到x12cm处所需的最短时间;(3)在x12cm处物体的总能量.2解:由题已知A2410m,T4.0s21∴0.5radsT又,t0时,xA,000故振动方程为2x2410cos(0.5t)m(1)将t0.5s代入得2x2410cos(0.5t)m0.17m0.52Fmamx3231010()0.174.210N2方向指向坐标原点,即沿x轴负向.(2)由题知,t0时,0,06
Att时x0,且v0,故t232∴t/s323(3)由于谐振动中能量守恒,故在任一位置处或任一时刻的系统的总能量均为12122EkAmA2213221010()(0.24)2247.110J11、图为两个谐振动的xt曲线,试分别写出其谐振动方程.3解:由题图(a),∵t0时,x0,v0,,又,A10cm,T2s000221即radsT3故x0.1cos(t)ma2A5由题图(b)∵t0时,x,v0,00023t1时,x10,v10,12255又11325∴655故x0.1cos(t)mb6312、一物块在水平面上作简谐振动,振幅为10cm,当物块离开平衡位置6cm时,速度为24cm/s。问:(1)此简谐振动的周期是多少?(2)物块速度为12cm/s时的位移是多少?解:设,已知,故,7
(1)当(2)当时13、一长方形木块浮于静水中,其浸入部分高为a,今用手指沿竖直方向将其慢慢压下,使其浸入部分高度为b,然后放手任其运动。试证明若不计阻力,木块的运动为简谐振动,并求出振动周期和振幅。解:xxObaS设木块质量为m,底面积为S,水的密度为,木块受到重力和浮力.平衡时,,以水面上某点为原点,向上为x轴建立坐标系,则当木块在图示位置时,合力为8
由牛顿第二定律故可见,木块作简谐振动,振幅为,,314、有一单摆,摆长l1.0m,摆球质量m1010kg,当摆球处在平衡位置时,若给小球一水41平向右的冲量Ft1.010kgms,取打击时刻为计时起点(t0),求振动的初位相和角振幅,并写出小球的振动方程.解:由动量定理,有Ftmv04Ft1.010-1∴v0.01ms3m10101按题设计时起点,并设向右为x轴正向,则知t0时,x0,v0.01ms>000∴3/20g9.81又3.13radsl1.02v02v00.013∴Ax()3.210m03.13故其角振幅A33.210radl小球的振动方程为333.210cos(3.13t)rad215、有两个同方向、同频率的简谐振动,其合成振动的振幅为0.20m,位相与第一振动的位相差为,69
已知第一振动的振幅为0.173m,求第二个振动的振幅以及第一、第二两振动的位相差.解:由题意可做出旋转矢量图如下.由图知222AAA2AAcos3021122(0.173)(0.2)20.1730.23/20.01∴A0.1m2设角AAO为,则1222AAA2AAcos1212222222A1A2A(0.173)(0.1)(0.02)cos即2AA20.1730.1120即,这说明,A与A间夹角为,即二振动的位相差为.1222216、已知两简谐振动的振动方程分别为和,试求其合成运动的振幅及初相。解:由,知:合成震动振幅为初相为10
17、试用最简单的方法求出下列两组谐振动合成后所得合振动的振幅:x5cos(3t)cmx5cos(3t)cm1133(1)(2)74x5cos(3t)cmx5cos(3t)cm22337解:(1)∵2,2133∴合振幅AAA10cm124(2)∵,33∴合振幅A018、一质点同时参与两个在同一直线上的简谐振动,振动方程为x0.4cos(2t)m165x0.3cos(2t)m26试分别用旋转矢量法和振动合成法求合振动的振动幅和初相,并写出谐振方程。5解:∵()66∴AAA0.1m合1250.4sin0.3sinA1sin1A2sin2663tanAcosAcos5321220.4cos0.3cos66∴6其振动方程为x0.1cos(2t)m6(作图法略)19、如图所示,两个相互垂直的谐振动的合振动图形为一椭圆,已知x方向的振动方程为x6cos2tcm,求y方向的振动方程.11
3解:因合振动是一正椭圆,故知两分振动的位相差为或;又,轨道是按顺时针方向旋转,故知22两分振动位相差为.所以y方向的振动方程为2y12cos(2t)cm212'
您可能关注的文档
- 大气污染控制工程第三版课后习题答案(18章全).doc
- 大气污染控制工程第三版课后习题答案(1~8章全).doc
- 大气污染控制工程答案.doc
- 大气污染控制工程课后习题答案(蒋文举版).pdf
- 大气污染控制工程课后习题答案.doc
- 大气污染控制工程课后答案郝吉明.doc
- 大气污染控制工程课后题答案.doc
- 大气污染控制工程郝吉明第三版课后答案郝吉明.doc
- 大物(第四版)-祝之光-课后习题解答.doc
- 大连交通大学《数据库原理及应用》刘金玲版(56课时)习题参考答案.doc
- 大连理工大学《工程制图》习题集答案.pdf
- 大连理工大学《汽车构造》试题及答案(共八套).doc
- 天大无机化学_课后习题参考答案.doc
- 天津大学《反应工程》(第二版)课后习题答案(2014年修改).doc
- 天津大学第五版有机化学答案.doc
- 天津大学高等教育出版社第五版《物理化学》课后习题答案第七章.doc
- 天津大学高等教育出版社第五版《物理化学》课后习题答案第五章.doc
- 天津市领导干部网上学法用法课后习题(含答案).docx