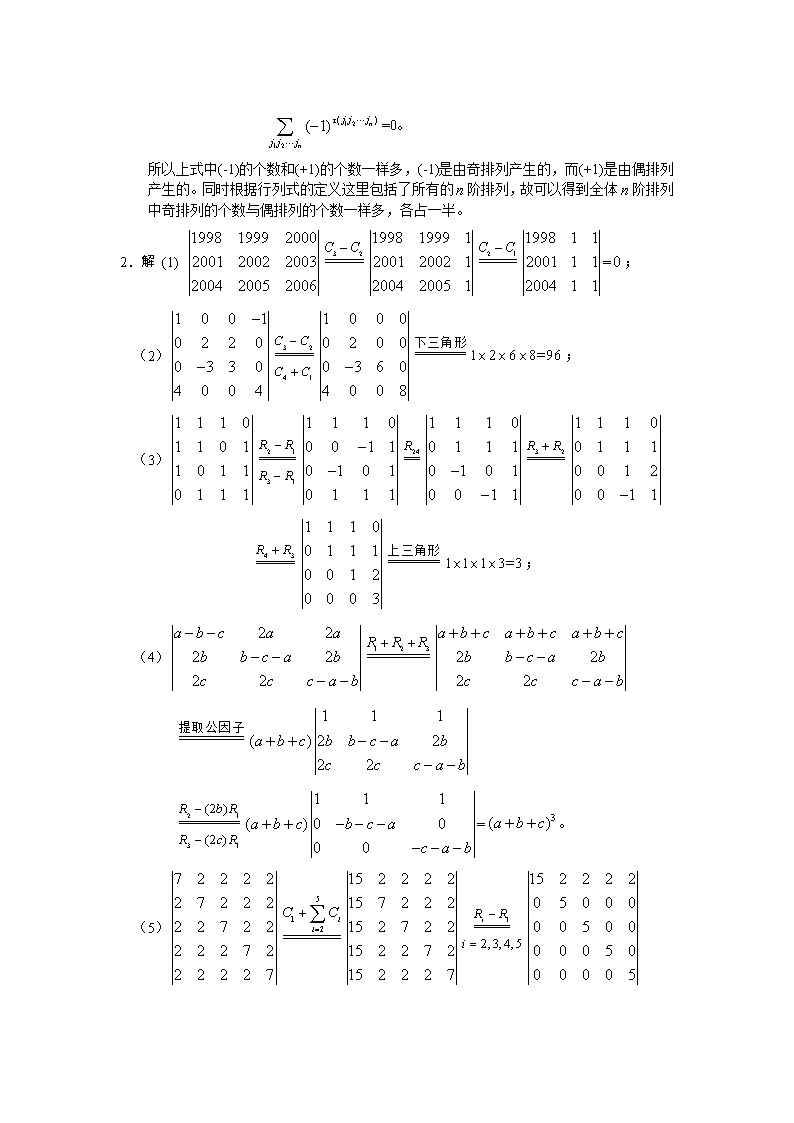- 3.15 MB
- 2022-04-29 13:54:41 发布
- 1、本文档共5页,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,可选择认领,认领后既往收益都归您。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细先通过免费阅读内容等途径辨别内容交易风险。如存在严重挂羊头卖狗肉之情形,可联系本站下载客服投诉处理。
- 文档侵权举报电话:19940600175。
'第一章行列式习题1.11.证明:(1)首先证明是数域。因为,所以中至少含有两个复数。任给两个复数,我们有。因为是数域,所以有理数的和、差、积仍然为有理数,所以。如果,则必有不同时为零,从而。又因为有理数的和、差、积、商仍为有理数,所以。综上所述,我们有是数域。(2)类似可证明是数域,这儿是一个素数。(3)下面证明:若为互异素数,则。(反证法)如果,则,从而有。由于上式左端是有理数,而是无理数,所以必有。所以有或。如果,则,这与是互异素数矛盾。
如果,则有,从而有“有理数=无理数”成立,此为矛盾。所以假设不成立,从而有。同样可得。(4)因为有无数个互异的素数,所以由(3)可知在和之间存在无穷多个不同的数域。2.解:(1)是数域,证明略(与上面类似)。(2)就是所有的实部和虚部都为有理数的复数所组成的集合。而复数域。(3)不是数域,这是因为他关于除法不封闭。例如。3.证明:(1)因为都是数域,所以,从而。故含有两个以上的复数。任给三个数,则有且。因为是数域,所以有且。所以。所以是数域。(2)一般不是数域。例如,我们有,但是。习题1.22.解:项的符号为习题1.31.证明:根据行列式的定义=
=0。所以上式中(-1)的个数和(+1)的个数一样多,(-1)是由奇排列产生的,而(+1)是由偶排列产生的。同时根据行列式的定义这里包括了所有的阶排列,故可以得到全体阶排列中奇排列的个数与偶排列的个数一样多,各占一半。2.解(1)=;(2);(3);(4)=。(5)
。3.解:(1)。(2)左端==右端。(3)。(4)原式(先依次)=。。。=。(5)原式(先依次)=。。。=。4.解:设展开后的正项个数为。则由行列式的定义有。又因为(利用)(下三角行列式)。所以有。
5.证明:(1)左端=右端。(2)利用性质5展开。6.解:(3)与上面3(3)类似可得。7.解:利用行列式的初等变换及性质5。8.解:。9.证明:设原行列式=D。则对D进行依次如下变换后所得的行列式D′第一列由题设中所给的5个数字构成。从而由行列式的定义可知D′可被23整除。又由行列式的性质知D′。因为23是素数,且不可能被23整除,所以D可以被23整除。习题1.41.解:(1)=;
(2)=;(3)方法一+=;方法二逐次均按第2行展开可得同样结果,具体解法可参见下例。(4)逐次按第2行展开===;(5)
==;(6)==;(7)换行后可得到范德蒙行列式;(8)先把第一行加到第三行,再提取第三行的公因式,换行后可得到范德蒙行列式。2.解:(1)+=;(2)=1+;(此处有笔误)
(3)=,据此当时,原式=;当时,原式=。3.解:(1)将按第n列展开得:=+=。(2)略(参考课本例中的叙述)。4.解:(1)交换行、列后得到三角块行列式,然后利用例1.4.6的结果;或者直接利用Laplace定理。(2)左端先做变换,再做变换,然后利用P30推论。5.解:(1)==;
(2)=;(3)利用初等变换。附加:P30推论的证明:证(1)将第r+1列与r列交换,由将新的r列与r-1列交换,如此继续,直到将第r+1列交换到第1列,这样共交换r次;再将第r+2列如上方法交换至第2列,也交换了r次,如此继续直到将r+s列交换至第s列.于是交换了rs次后得到=将所得行列式的第r+1行依次与第r行,r-1行,……,第1行交换.交换r 次后,r+1行交换至第1行.类似地交换r次后将r+2行交换至第2行,……,交换r次后将第r+s行交换至第s行,于是交换rs次后得:(2),(3)思路与(1)类似,证明过程略去。习题1.52.解:计算得=根据克拉默法则,当时,即时,原方程组只有零解。
习题1.61.证明:方法一归化==右端.方法二归纳法当时,=结论成立.假设时结论成立,即有则当时,将的第n列看成1+0,1+0,……,1+,故可表示为2个行列式之和,而第2个行列式按第n列展开可算出为从而=+而=.所以=+=+
==右端.方法三递推由证明(二)可知与存在以下递推关系:=+所以=+====右端.方法四加边法===右端。2.证明:(1)注意当把行列式按第n列展开时,得到的递推公式中有三项,故归纳法第一步应验证n=1,2时均成立。而归纳法第二步应假设当时成立,去证明当n=k时成立。3.解:(2)先把除第一列外的所有列都加到第一列,然后提出第一列的公因子;再依次;然后按第一列展开,再依次;最后按最后一列展开。4.解:通过倍加行变换易知f(x)的次数最大为1;又因为如果全取零,则有f(x)=0。所以选(D)。5.看自己或别人的作业。6.解:方法一:利用课本中例1.4.3的方法。
方法二:设。则有f(x)中的系数为。又因为(范德蒙行列式),所以f(x)中的系数为。。。所以可得。第一章线性方程组习题2.12.证明.因,说明不全为零,故当某个,通过适当的行互换,可使得位于左上角,用来乘第一行,然后将其余行减去第一行的适当倍数,矩阵A可以化为:,由于,此时必有,故可以对重复对A的讨论,此时A可经初等行变换化为,然后再将第行的倍加到第行(),再将第行的倍加到第行(),这样继续下去,一直到将第2行的倍加到第1行,此时A就化为,故所证结论成立。3.证明:以行互换为例:列互换可以同样证明.
若,这相当于A中交换第i行和第j行,所以结论成立。习题2.21.解:中一定存在不为零的阶子式,否则秩,与题设秩()=矛盾.由秩()=知,中至少存在一个阶子式不为零,这表明中的阶子式只要有一个不为零即可,其余可以等于零,也可以不等于零.中一定不存在不为零的阶子式,否则的秩至少是,这也与题设秩()=矛盾。2.提示:利用矩阵的行秩和向量的极大无关组证明。3.略。4.思路:可将矩阵写成一个列向量和一个行向量的乘积,从而由秩;进而因为矩阵不等于零,所以秩〉0。5.略。习题2.3略。习题2.4
2.证明:(Ⅰ)的增广矩阵为=,因为系数矩阵的秩不超过增广矩阵的秩,所以有秩()秩().观察可知,矩阵其实就是在增广矩阵下面加了一行,所以秩()秩().由题意知,秩()=秩(),据此可得秩()秩().综上知秩()=秩(),故(Ⅰ)有解。3.解:将增广矩阵只用初等行变换化为阶梯形矩阵.当时,秩()秩(),所以线性方程组无解;当时,秩()=秩()<未知量个数,所以线性方程组有无穷多解.原方程组同解于
故通解为其中为任意常数。4.证明:该线性方程组的增广矩阵=,由题意知秩()=.但是系数矩阵是一个的矩阵,所以秩()<秩().据此秩()秩(),所以该线性方程组无解。第一章矩阵习题3.14.解:(1)由矩阵乘法运可得:;。(2)与D乘法可换的矩阵满足。故与的元素对应相等,利用(1)的结果,有,从而。由于(),可得:当时,,即为对角矩阵。5.证明:(1)数学归纳法:当时,计算得,故结论成立.假设当时,结论成立,即有,则当时,
.因所以,即当时,结果成立.由归纳法原理知,对任意大于2得正整数有.(2)当时,结果显然成立.当时,直接计算得.假设当时,结果成立,即.我们要证明当时,结果也成立,即可完成证明.第一种情况:k为奇数,则.第二种情况:k为偶数,则.综上:即当时,结论成立.1.解:(1)先计算出时的结果。然后归纳出应该有,接下来用数学归纳法证明这一归纳出的结果。当时,结论显然成立.假设当时,结论成立,即.则当时,
结论成立.7.记住结论。8.证明:因为与所有n阶方阵乘法可换,故与乘法可换,利用第7题结果有,即.设,则即为数量矩阵.10.证明:设,,则tr同理可得tr由于,可得trtr.11.证明:假如存在n阶方阵满足,则trtrtr.
由于,可得trtr,这与10题所得结果矛盾.所以假设不成立.即不存在n阶方阵,满足.15.证明:因,都是对称矩阵,故,从而为对称矩阵.16.证明:设,则.由的主对角线上元素为零,由为实数知.证法二:利用二次型。习题3.24.思路:注意到矩阵多项式的运算和一般多项式的运算一样就可以了。证明:计算,由题意可知,所以.根据定理3.2.1的推论可知可逆且其逆为.5.证明:计算==计算据此,根据定理3.2.1的推论可知可逆且其逆为.
6.证明:因为所以有.由题意可知,所以可在等式两边同乘上,由此可得,整理得,根据定理3.2.1的推论可知可逆且.7.证明:(1)由题意可得,根据定理3.2.1的推论可知可逆并且.(2)由题意可得,而这个等式可化为,即有,同样根据定理3.2.1的推论可知可逆并且.8.思路:注意题设实际上是给出了矩阵多项式。所以一般情况下,如果可逆,其逆矩阵也应该是一个矩阵多项式。所以我们可以假设其逆矩阵为(待定系数法),从而由逆矩阵定义知应该有,即。在注意到题设是,所以我们有,所以有,即。证明:因为,所以。所以。。。9.证明:(1);(2)由于,所以,由此可得;(3);
(4);(5)由(2)中分析可知,所以;(6)由(2)中分析可知,则。10.证明:都可逆,所以有,由此可知,从而得到.另一方面,由于都可逆且均为阶方阵,所以也可逆,所以有,而.综合上述可得.11.略。12.证明:假设是可逆矩阵,那么在等式两边都左乘的逆矩阵可得,这与题设中矛盾!所以不可逆.13.证明:根据题意可知存在非零的n×t矩阵B使AB=O,B是非零矩阵所以必存在某一列上的元素不全为零,不妨设这一列为.由于,所以,据此可知是线性方程组的一个非零解.由于有非零解,所以=0.14.略。15.解:(A)可逆的充要条件是而不是,设,但不是可逆矩阵,所以选项(A)是错误的.(B)设,显然都是可逆的,但是不是可逆矩阵,所以选项(B)是错误的.(C)可逆的充要条件是而.所以选项(C)是正确的.
(D)不可逆的充要条件是;而中至少有一行全为零只是的充分条件。设,但不是可逆矩阵,所以选项(D)是错误的.习题3.31.解:(1)设,则原式可以分块写成,利用分块矩阵的性质计算得而,,据此可得.(2)设则原式可以分块写成,利用分块矩阵的性质计算得而,.
据此可得.2.解:(1);(2);(3);(4);(5)。3.证明:(1)先证“”,当可逆时,则必有.而,所以有,从而有,因此均可逆.再证“”,均可逆,则有,所以有,而,所以,据此可知可逆.综上即有Q可逆A,B均可逆.(2)设,则有而,所以有,因为可逆,由(1)可知必有可逆,所以由,可得.而由,可得
.所以.5.解:(1)设,则原矩阵为.而.因为,所以可得.习题3.44.解:(1)A中行与行互换相当于用初等矩阵左乘得到.由于,而=,所以相当于右乘了初等矩阵,即中的列与列互换.(2)A中行乘上非零数相当于用初等矩阵左乘得到.由于,而=,所以相当于右乘了初等矩阵,即中行乘上非零数.(3)A中第行乘上数加到第行相当于用初等矩阵左乘得到.由于,而=,所以相当于右乘了初等矩阵,即中第行乘上数-加到第行.7.解:由于,所以,即有
,变形得,从而有.而,显然是可逆矩阵.所以只需要求出即得到.下面只用初等行变换把化为即可.,从而得到。习题3.51.证明:设为秩为r的矩阵,则它必与矩阵等价,所以必存在两个可逆矩阵使得成立.而可以写成r个只有一个元素为1其余为零的矩阵的和的形式:
所以有==这样就表示成了r个矩阵之和的形式.而任一个,由于中间那个矩阵只有一个元素非零,所以其秩为1,而可逆,所以三个矩阵的积的秩仍然为1.这样就表示成了r个秩为1的矩阵之和了.2.解:设
显然的秩都是1,但是他们的和的秩是1而不是r.所以该逆命题不成立.5.证明:因为列满秩,所以存在可逆矩阵使得,所以。进而有。所以令即可。7.证明:(1)因为,所以结论成立。(2)由(1)知不满秩,所以不可逆。(3)略。8.证明:因为,所以。所以。同理有。9.解:设,计算得.显然秩()=1,秩()=0,两者不相等.所以秩()与秩()不一定相等.10.解:设秩()=,秩()=,则存在四个可逆矩阵使得成立.令,首先因为都是可逆矩阵,所以也是可逆的.又因为秩()+秩()≤n,
即+≤n,所以的前行列构成的块是一个零块,因此可以写成下面这个形式.计算所以存在可逆矩阵使得.习题3.61.解:(1)设,易知,但,所以(1)不一定成立.(2)设,易得,此时,所以(2)不一定成立.(3)设,易得所以(3)不一定成立.(4)设,易得,此时,所以(4)不一定成立.(5)(6)都是课本中提及的性质,是成立的.(7),所以(7)成立.2.解:(1)设,则显然此时,所以该项不一定成立.
(2)设,则计算得,而中由于第二第四两行相同,所以.因此此时,所以此项不一定正确.(3),所以不正确.(4),所以不正确.(5)因为A,B为可逆矩阵,所以方程两边同左乘,再右乘即得.所以是正确的.(6)因为,所以秩()=1=秩(),因此这两个矩阵等价.3.证明:(1)因为秩()=r,所以与等价,即存在两个可逆矩阵使得,令,因为是可逆的而的秩都为,所以秩()=秩()=r.并且是的,是的.而且计算可得.(2)只需令,同(1)分析可知这样构造得
到的即为所需的两个矩阵.(3)只需令,同(1)分析可知这样构造得到的即为所需的两个矩阵.4.记住此结论。5.证明:因为,所以由题设知。又因为,所以。第一章线性空间和线性变换习题4.12.记住此结论。习题4.210.证明:设使得,则有。因为线性无关,所以。所以。习题4.33.证明:设向量组(I)、(II)的极大无关组分别为(III)、(IV)。则有(I)与(III)等价,(II)与(IV)等价。所以(III)能用(I)线性表示,(II)能用(IV)线性表示。因为(I)能用(II)线性表示,所以(III)能用(IV)线性表示。因为(III)线性无关,所以(III)中所含向量的个数(IV)中所含向量的个数,即秩(I)秩(II)。4.证明:由题设易知向量组可由线性表示,下面只需证明可由线性表示即可。因为可由线性表示,所以存在数使得。因为不能经线性表示,所以
。所以,即可由线性表示。5.证明:因为线性相关,所以存在不全为零的数使得γ=0。下面分情况对是否为零进行讨论(四种情况)。略。6.证明:(1)因为,,线性无关,所以,必线形无关,又因为,,线性相关,所以能经,线性表示,并且表示方法唯一.(2)若能经,,线性表示,不妨设表达式为,根据(1)能经,线性表示,不妨设表达式为,把带入到中得即有,从而得到,,线性相关,这与题意中,,线性无关矛盾!所以不能经,,线性表示.习题4.43.解:由=,可得秩()=4,这四个向量线性无关,所以该向量组是中的一组基.因为,所以方程组的解为
所以向量在该基下的坐标为。4.解:(1)由=可知的解为所以=2+.同样可计算得=++;=+3.所以从基(Ⅰ)到基(Ⅱ)的过渡矩阵为.(2)=,所以坐标为。8.解:因为,所以秩()=4,所以可作为的一组基.设向量,则它在常用基下的坐标为.则有,即要求.求解方程组得解为,所以所求的向量(为任意值).
习题4.51,2.思路:验证3条。5.思路:即证与等价。习题4.62.思路:即说明这是解空间的一组基。4.思路:注意要指出齐次线性方程组的基础解系只含有一个向量。7.证明:(1)因为,所以秩()+秩(),由于秩()=,所以秩(),由此秩()=0,即得.(2)由题意知,所以,利用(1)可知,因此.9.证明:先证必要性,根据等价标准形可知存在矩阵,秩()=秩()=1,使=.令为的个分量,为的个分量,则因为秩()=秩()=1所以和都不全为零.同时因为=即得(=1,2,…,;=1,2,…,)成立.再证充分性,根据题意存在个不全为零的数及n个不全为零的数使(=1,2,…,;=1,2,…,).只需令,则=.因为秩()秩(),又由于和都不全为零,所以中必有一非零元素,因此秩()>0,据此可得秩()=1.10.证明:(1)由于秩()=n,所以,而,在等式两边同乘可得,据此可知是可逆的,所以秩()=n.(2)秩()<n-1时,根据矩阵秩的定义可知的所有阶子式都为0,而的元素就是的所有阶子式,所以的元素都是0,即=,所以秩()=0.
(3)当秩()=n-1时,不是满秩的,所以.又因为,所以,据此可知秩()+秩(),而秩()=n-1,所以秩().同时由于秩()=n-1,根据矩阵秩的定义可知至少有一个阶子式不为零,而的元素就是的所有阶子式,所以中至少有一个元素不为零.由此可知秩(),所以秩()=1.14.思路:利用分块矩阵。习题4.86.证明:因为与均正交,所以因此,所以与的线性组合都正交.7.解:设,根据题意为单位向量可知.(1)同时与都正交,据此可得从而可解得(其中为任意取值).又因为条件(1)可知,所以=.11.解:(1)因为=,所以是的一组标准正交基.(2)由(1)知;
因为在下的坐标为,而在下的坐标为=,所以()=(,).15.解:因为,所以方程组的一个基础解系为先进行正交化得到;再进行单位化得到;.所以即为所求的标准正交基.习题4.112.证明:(1)因为的解均为的解,所以的基础解系中的解也都是的解,所以的基础解系中所含的向量的个数不少于的基础解系中所含向量的个数.而的基础解系中所含的向量的个数为n-秩(B),的基础解系中所含向量的个数为n-秩(A),因此n-秩(B)n-秩(A),所以秩(A)≥秩(B).(2)因为与同解,所以的基础解系也就是的基础解系,所以两者的基础解系所含向量个数相同,因此n-秩(B)=n-秩(A),即有秩(A)=秩(B).(3)因为秩(A)=秩(B),所以n-秩(B)=n-秩(A),据此可知和
的基础解系所含向量的个数相同.因为的解均为的解,所以的某一基础解系(n-秩(A))也都是的解,如果与不同解,则的解中存在一个解不是的解,则一定不能被线性表示,所以线性无关,这样的解中至少含有个解线性无关,即的基础解系所含向量的个数大于等于,这与和的基础解系所含向量的个数相同矛盾.所以与不同解的假设是不成立的,因此与同解.(4)设,显然满足秩(A)=秩(B),但是是的一个解,但是不是的解.所以不能导出与同解.3.证明:首先由题设可得齐次线性方程组同解。然后去证明。4.证明:易证明的解都是的解,又因为秩(CA)=秩(A),根据本节第2个习题(3)可知和同解.同样易证的解都是的解.另一方面,设是的任意一个解则有,即,可知是的一个解,已经证明和同解,所以也一定是的解,即有,所以也就是的解,据此可得的解也一定是的解,所以和同解.根据本节第2个习题(2)可得秩(CAB)=秩(AB).5.证明:6.证明:(1)要证,即证,等价与证明。因为保持内积,所以由内积的双线性性得。第一章特征值和特征向量矩阵对角化
习题5.11.解:(A)设,因为秩()=秩()所以与等价;但是由于tr与tr不相等,所以与不相似.因此(A)不正确.(B)与相似,即存在可逆矩阵使得,所以秩()=秩(),因此与等价.(B)是正确的.(C)与(A)一样,设,秩()=秩(),但是由于tr与tr不相等,所以与不相似.因此(C)不正确.(D)与(A)一样,设,||=||,但是由于tr与tr不相等,所以与不相似.因此(D)不正确.7.解:(1)因为,所以特征值为1,1,3.求解方程组,得属于特征值1的特征向量为(其中为不同时为零的任意数).求解方程组,得属于特征值3的特征向量为(其中为不为零的任意数).习题5.24.证明:的特征多项式为而是A的特征多项式,所以A与有相同的特征多项式.
6.解:因为1是A的一重根,所以(E-A)X=O的基础解系含有1个向量,因此3-秩(E-A)=1,从而可知秩(E-A)=2.又因为2是A的二重根,所以(2E-A)X=O的基础解系含有向量的个数为1或2,由于A不能与对角矩阵相似,则可知A的线形无关的特征值个数小于3,所以(2E-A)X=O的基础解系含有向量的个数只能为1,同样可得3-秩(2E-A)=1,所以秩(2E-A)=2.7.解:因为,所以的特征值为-1,1,1.因为与对角矩阵相似,所以要求特征根的重数与的基础解系所含向量个数相等.-1是一重根所以一定满足,所以只要特征值1满足即可.也就是要求的基础解系含有2个向量,由此可知-秩()=2,因此秩()=1.因为,所以当且仅当时秩()=1,所以能与对角矩阵相似,则必有。习题5.32.解:因为秩(A)=1=秩(B),所以A与B等价.又因为trA=4,trB=1,即有,所以A与B不相似.综上可知(B)是正确的.3.解:(1)因为,所以。因为有三个不同的特征值,所以也可以对角化。所以的所有特征值为。(2)||=.5.解:(1)因为,所以特征值为2,2,-7.
求解方程组,得到属于2的线形无关的特征向量为.对进行施密特正交化化为正交单位向量组得。求解方程组,得到属于-7的线形无关的特征向量为.对进行施密特正交化化为正交单位向量组得。所以,其中.由此可得.(2)的特征值为,所以==.
6.解:因为方阵A的n个特征值为1,2,…,n,所以可以对角化。所以A+E的特征值为2,3,……,n,n+1.所以|A+E|=.11.证明:因为,所以是A的n重根.如果A能与对角矩阵相似,则必有的基础解系含有个向量,即-秩()=n,也就是秩()=0,从而得到此时,即,这与条件矛盾!所以A不能与对角矩阵相似.12.证明:因为,所以,即-2是A的一个特征值。设为A的特征值,是A的属于的特征向量,则有,所以,从而可得,即得,所以A的特征值仅为-2.习题5.41.证明:设是反对称矩阵的一个特征值,是的属于的特征向量,则有.(1)令,其中表示的共扼复数,.对(1)式两边同取共扼得.因为是实矩阵,所以有,因此有.(2)对(1)式两边转置得,因为是反对称矩阵,所以从而.(3)对(2)式两边同左乘,对(3)式两边同右乘,分别得,从而得=,移项得,因为,所以,
所以为零或者纯虚数.2.解:(3)因为,所以特征值为1,1,1,5.解线性方程组,得属于特征值1的线性无关的特征向量为.解线性方程组,得属于特征值5的线性无关的特征向量为.所以,对角矩阵为.3.解:(3)先对属于特征值1的三个特征向量进行正交化..;;.再对向量进行单位化,得到三个正交单位向量.,,,再对属于特征值5的特征向量进行单位化得.
由此得到,对角矩阵为.4.证明:显然成立.因为A,B有相同的特征多项式,则A,B必有相同的特征根.不妨设这些根为,因为A,B均为n阶实对称矩阵,所以存在可逆矩阵使得.由此可知,所以有,其中是可逆的,因此A与B相似.1.解:因为,所以特征值为0,2,2.(然后验证可对角化,从而可对角化)因为(其中),所以的特征值为所以.习题5.55.解:因为,所以A的特征值为一个一重特征值和一个重特征值.因为秩()=,所以与重数相同.因为秩()=,所以与重数相同.所以A
能对角化(也可由实对称矩阵得到),与其相似的对角矩阵为.6.证明:设为n阶方阵A的特征值,为A的属于的特征向量,则有.所以,即有,因此A的特征值或为1,或为-1.7.解:(1)因为矩阵A与B相似,所以trA=trB,,由此可以得到,从而可知.当时,易知A的特征值为2,2,6.求解方程组,得到属于2的线形无关的特征向量为.求解方程组,得到属于6的线形无关的特征向量为.所以此时可以对角化。类似可以证明此时也可以对角化。所以由他们的特征值相同可以知道此时与合同。(2)由(1)可知.8.解:因为,所以A
有一个两重特征值1和一个两重特征值2.秩(),秩(),A能与对角矩阵相似所以必有.因此要求秩()=秩()=2.,要使得秩()=2,必有;,要使得秩()=2,必有.综上,.10.解:(1)由可得三个方程,解之可得结果。(2)略。第一章二次型习题6.12.解:(1),令因为,所以线性替换是非退化的.从而得到标准形.(4)先令则==
令则因为,所以先行替换是非退化的.从而得到标准形.3.解:(1)错,因为,所以线形替换是退化的,所以错.正确的为=,其中线性替换为因为,所以该线形替换是非退化的.(2)错,因为,所以线形替换是退化的,所以错.正确的为=其中线性替换为因为,所以该线形替换是非退化的.习题6.21.解:3.解:(1)
计算特征多项式,得到特征值为1,2,5.解方程,得到属于1的线形无关的特征向量为.解方程,得到属于2的线形无关的特征向量为.解方程,得到属于5的线形无关的特征向量为.三个向量已经两两正交,所以只要单位化即可得到,,.所以,因此正交变换为,而标准型为.6.证明:(1)设,令(满足),则有,再令(满足),则有,因为,并且由于A是一个n阶对称矩阵所以有,所以由可得,因此.
(2)若存在两个对称矩阵使得,则两式相减得对任意成立.由于都是对称矩阵,所以两者的差也是对称矩阵,根据(1)可知,从而得到.8.证明:因为是的一个排列,所以可以通过若干次互换变成.而每次互换就相当于交换的位置,由第8个习题可知这就相当于同时左乘右乘同一个互换得到的初等矩阵.由此可知.设,则所以得到,因此矩阵与合同.习题6.33.证明:与习题3.5T1类似,只不过要把右边的可逆矩阵换成左边的转置。4.解:因为两个矩阵合同的充要条件是有相同的秩和相同的正惯性指数,按秩从0,1,2,到n有n+1大类,秩为0时正惯性指数只有一种可能就是0;秩为1时正惯性指数有0,1两种可能,秩为2时正惯性指数有0,1,2三种可能;……;秩为n时正惯性指数有0,1,2,……,n共n+1种可能.所以一共有1+2+……+n+1=种可能,所以一共有多个合同类.秩为,正惯性指数为的合同类中最简单的矩阵是一个对角矩阵它主对角线上前个元数为1,中间个元素为-1,其他为0.6.解:(1)不正确,令,显然A
与B合同,C与D合同,但是A+C,B+D,两者秩不同所以不合同.所以(1)不正确.(2)正确,A与B合同,C与D合同,所以存在两个可逆矩阵满足.令,因为可逆,所以也可逆.又有,所以与合同.因此(2)是正确的.习题6.42.解:正定,首先要求A是对称矩阵,所以有.还必须要求三个顺序主子式都大于零.所以要求.因此要求,所以选(A).6.解:(1)的矩阵为,要求二次型正定即要求所有顺序主子式,由此可得时此二次型正定.6.解:因为是正定矩阵,所以是正定二次型,所以对于任意非零向量都有.现令
(满足),则有.8.证明:(1)参看下面部分的证明。(2)因为为正定矩阵,所以对任意的n维非零向量都有,即有,所以不存在非零向量使得,因此可得秩(A)=n..首先显然是一个对称矩阵,现取任意一个n维非零向量,不妨设则,并且当且仅当时取到0.又因为秩(A)=n所以只有零解,而是非零向量,所以,因此,由此可得为正定矩阵.9.证明:(2)假设秩(P)
您可能关注的文档
- 《管理运筹学》第二版习题答案(韩伯棠教授)高等教育出版社,超详细版.doc
- 《精品》电大本科专科公共管理学答案期末考试真题全集.doc
- 《系统解剖学》习题参考答案.doc
- 《系统解剖学》复习题及参考答案.doc
- 《红楼梦》章回练习及答案(第1-120回).doc
- 《纤维化学与物理》练习题.doc
- 《纲要》思考题答案.doc
- 《线性代数》(魏_ 黄)习题解.doc
- 《线性代数》同济大学第四版课后答案.doc
- 《组织行为学》练习册答案.doc
- 《细胞生物学》习题及解答.doc
- 《经济博弈论》课后答案、补充习题答案.doc
- 《经济地理学 第二版》课后思考题答案.doc
- 《经济地理学》第二版课后思考题答案.doc
- 《经济地理学》课后思考题答案.doc
- 《经济学基础》习题试卷与答案.doc
- 《经济学基础》各讲习题及参考答案(简).doc
- 《经济应用数学—概率论与数理统计》马统一的习题1一5答案.doc