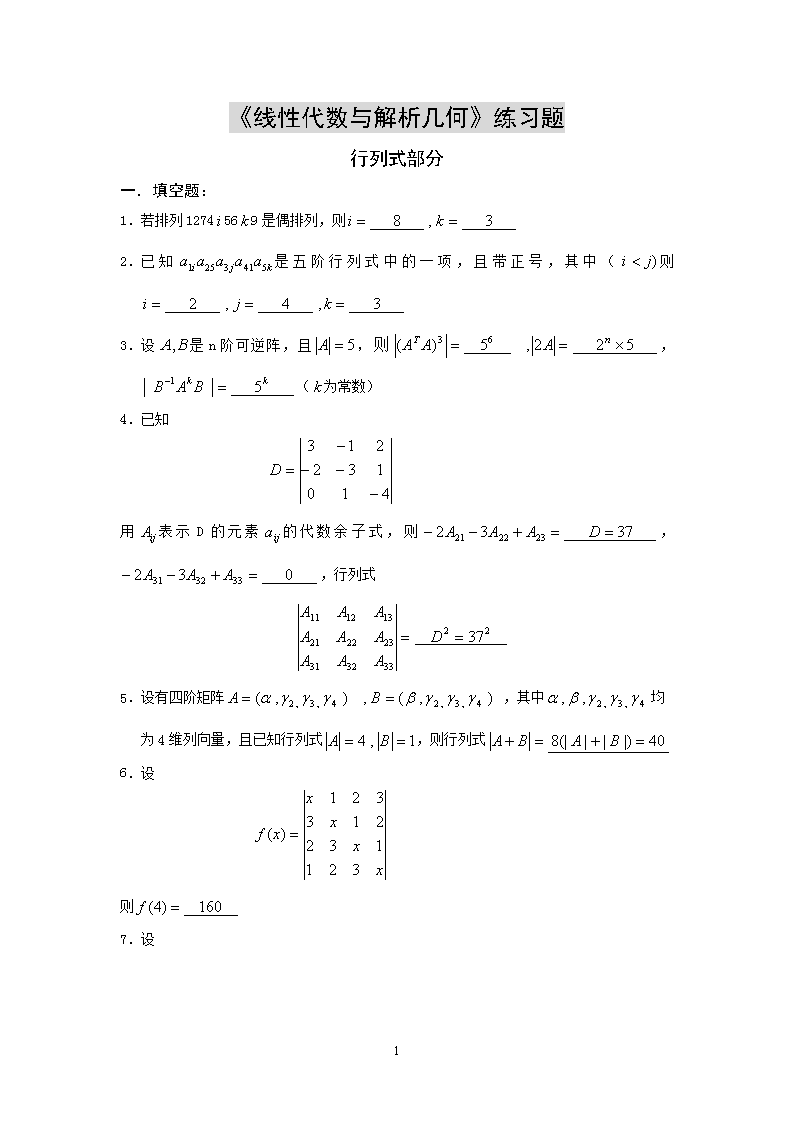- 1.34 MB
- 2022-04-29 14:09:24 发布
- 1、本文档共5页,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,可选择认领,认领后既往收益都归您。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细先通过免费阅读内容等途径辨别内容交易风险。如存在严重挂羊头卖狗肉之情形,可联系本站下载客服投诉处理。
- 文档侵权举报电话:19940600175。
'《线性代数与解析几何》练习题行列式部分一.填空题:1.若排列1274569是偶排列,则2.已知是五阶行列式中的一项,且带正号,其中(则3.设是n阶可逆阵,且,则,(为常数)4.已知用表示D的元素的代数余子式,则,,行列式5.设有四阶矩阵,其中均为4维列向量,且已知行列式,则行列式6.设则7.设20
上述方程的解8.设A是阶方阵,且A的行列式,而是A的伴随矩阵,则9.若齐次线性方程组只有零解,则应满足条件。二.计算题:1.已知5阶行列式求和,其中是元素的代数余子式。解:2.计算行列式。解:3.设是阶方阵,,且,求。20
解:1.设是阶实对称矩阵,,若,求。解:相似于对角阵,.而r(A)=k,所以。对于矩阵A+3I,有一个,以及一个,2.计算解:矩阵部分一.填空题:20
1.设三阶方阵A,B满足,且,则。2.设,其中,则矩阵A的秩=1.3.设A是的矩阵,且A的秩为2,而,则()4.已知a=[1,2,3],b=[],设A=,则()5.设矩阵则逆矩阵6.设,B为三阶非零矩阵,且AB=O,则7.设四阶方阵A的秩为2,则其伴随矩阵的秩为0。20
1.设A,B均为阶矩阵,,则2.设A是三阶方阵,是A的伴随矩阵,,则()。10.设A,C分别为阶和阶的可逆矩阵,则分块矩阵的逆矩阵11.设阶方阵A满足方程,则A的逆矩阵()12.设,而为正整数,则13.设A,B是阶矩阵,且AB=A+B,则()二.选择题:1.设阶矩阵A,B,C满足关系式ABC=E,其中E是阶单位矩阵,则必有(D)(A)ACB=E(B)CBA=E(C)BAC=E(D)BCA=E2.设A是阶方阵,是A的伴随矩阵,又为常数,且,则必有=(B)3.设A是阶可逆矩阵,是A的伴随矩阵,则有(A)4.设20
则必有(C)5.设A,B均为阶方阵,则必有(D)(A)(B)(C)(D)6.设维向量,矩阵,其中为阶单位矩阵,则(C)(A)0(B)–I(C)I(D)7.设A是阶可逆矩阵,是A的伴随矩阵,则(C)(A)(B)(C)(D)8.设阶矩阵,若矩阵A的秩为,则必为(B)(A)1(B)(C)–1(D)9.设均为阶可逆矩阵,则等于(C)(A)(B)(C)(D)二.计算题:1.已知,求(是自然数)20
解:由归纳法,1.已知AP=PB,其中,求:及。解:3.已知阶方阵求A中所有元素的代数余子式之和。解:2.已知矩阵满足:,其中,求矩阵。20
解:5.设矩阵,满足其中是A的伴随矩阵,求矩阵B。解:1.已知,且,其中为三阶单位矩阵,求矩阵。解:2.设阶方阵,求。解:故时,;时,r(A)=n-1;当a≠1且a≠1-n时,r(A)=n二.证明题:20
1.设A是阶非零方阵,是A的伴随矩阵,是A的转置矩阵,当时,证明。证明:另证(反证法):与题设矛盾。2.设是阶方阵,若,证明:(其中是A的伴随矩阵)证明:3.设,为的代数余子式,且,求证:证明:4.用矩阵秩和向量组秩的关系证明证明:设,即的列皆由的列线性表示,故类似可证的行皆由的行线行表示,所以。5.设为矩阵,为矩阵,若,证明证明:20
所以,即为齐次线性方程组的解,因此可由的基础解系线性表示,所以,即。1.设A是阶方阵,是A的伴随矩阵,证明:秩证明:(1)可逆,而可逆,(2),又A至少有一个n-1阶子式不为零,,从而(3)的所有n-1阶子式全为零。故,从而。空间向量与线性方程组部分一.填空题:1.设则2.点在平面上的投影点是(将其代入可得)1.过原点及点且与平面垂直的平面方程是2.平面上的直线绕轴旋转一周所得旋转曲面方程为3.曲线在平面上的投影曲线为4.已知向量组,则该向量组的秩.20
7.设阶矩阵的各行元素之和均为零,且的秩为,则线性方程组的通解为8.已知向量组的秩为2,则.9.若线性方程组有解,则常数应、满足条件。()10.若向量组()可由向量组()线性表示,则秩()秩()。二.选择题1.设直线,平面,则(B)(A)与平行(B)与垂直(C)在上(D)与斜交2.已知是非齐次线性方程的两个不同的解,是对应的齐次线性方程组的基础解系,为任意常数,则方程组的通解必是(B)1.使,都是线性方程组的解,只要系数为(A)20
4.已知向量组线性无关,则向量组(C)线性无关5.设是矩阵,是非齐次线性方程组所对应的齐次线性方程组,则下列结论正确的是(D)若仅有零解,则有唯一解若有非零解,则有无穷多个解若有无穷多个解,则仅有零解若有无穷多个解,则有非零解6.设有向量组,,,,则该向量组的极大线性无关组是(B)7.非齐次线性方程组中未知量个数为,方程个数为,系数矩阵的秩为,则(A)时,方程组有解时,方程组有唯一解时,方程组有唯一解时,方程组有无穷多解8.若向量组线性无关;线性相关,则(C)必可由线性表示必不可由线性表示必可由线性表示必不可由线性表示9.设向量可由向量组线性表示,但不能由向量组:线性表示,记向量组Ⅱ:,则(B)不能由线性表示,也不能由Ⅱ线性表示20
不能由线性表示,但可由Ⅱ线性表示可由线性表示,也可由Ⅱ线性表示可由线性表示,但不能由Ⅱ线性表示三.计算题1.求点向直线所作的垂线方程。解:,得出2.求异面直线与的距离。解:3.已知方程组的解空间的维数为2,求方程组的通解。解:4.设,求一个秩为2的3阶矩阵使。20
解:1.设三元非齐次方程组的系数矩阵的秩为2,且它的三个解向量满足求的通解。解:2.取何值时,线性方程组有唯一解,无解或有无穷多解?当方程组有无穷多解时求其通解。解:,方程组有唯一解,方程组无解,方程组有无穷多解3.已知及,问:(1)为何值时,不能由线性表示。(2)为何值时,有的唯一线性表示?并写出该表示式。20
解:,不能线性表示,四.证明题1.已知,证明:向量共面。证明:等式两边点乘向量c,得到,所以向量a,b,c共面。2.证明:三个平面经过同一条直线的充要条件是。证明:三平面经过同一条直线有非零解,3.已知,其中,三条直线,证明三条直线相交与一点的充要条件为线性无关,线性相关。证明:三条直线交于一点有唯一解其中4.已知向量组(Ⅰ);(Ⅱ);(Ⅲ)如果各向量组的秩分别为(Ⅰ)(Ⅱ)=,(Ⅲ)=。证明:向量组的秩为。20
证明:因为r(I)=r(II)=3,所以由于线性无关,得,所以r(III)=41.设向量组是齐次线性方程组的一个基础解系,向量不是方程组的解,即。试证明:向量组线性无关。证明:设两边左乘A,利用从而有线性无关相似矩阵及二次型部分一.填空题1)为3阶矩阵,若有特征值,则2)设为阶矩阵,,为的伴随矩阵,为阶单位阵,若有特征值,则必有特征值;的特征值。3)为阶矩阵的元素全为1,则的个特征值是n,0,0,……,0。4)二次型是正定的,则的取值范围是。5)n阶矩阵具有n个线性无关的特征向量是与对角阵相似的充要条件。6)n阶矩阵具有n个不同的特征值是与对角阵相似的充分条件。7)设为3阶矩阵,已知均不可逆,则一定相似于矩阵20
。8)已知相似,则。二.选择题1.设是非奇异矩阵的一个特征值,则矩阵有一特征值等于(B)()()()()2.若是矩阵的对应的特征向量,则矩阵对应的特征向量(A)()()()()3.设是的实矩阵,,则方程组只有零解是正定矩阵的(C)条件。()充分()必要()充要()既非充分也非必要三.计算题1.已知是的特征向量,其中,求及所对应的特征值。解:,解出k=1或k=-22.设是阶方阵,2,4,6,……,2n是的个特征值,是阶单位阵,求。20
解:1.已知三阶实对称矩阵的三个特征值为1,1,-2,且是对应的特征向量,求矩阵。解:设特征值对应的特征向量是,由,得,解此线性方程组,求出基础解系2.已知三阶矩阵相似于对角阵,试求。解:同理所以3.已知二次型的秩为2,(1)求参数及二次型对应矩阵的特征值。(2)写出标准形及所用的正交变换矩阵。解:(1),标准形为,正交变换矩阵为 4.设4阶方阵满足条件,求方阵的伴随矩阵的一个特征值。20
解:是矩阵A的一个特征值。四.证明题:1.设为实矩阵,为阶实对称矩阵且正定,证明:正定的充要条件是。证明:2.已知为幂零矩阵(),证明:证明:3.设维向量线性无关,且与都正交,证明:线性相关。证明:若,则线性无关,而线性相关可由线性表示,且表示法唯一设,则,从而线性相关。20
1.设为阶矩阵且正定,为实维列向量,当时,有证明:线性无关。证明:令,两边左乘得:20'
您可能关注的文档
- 《管理运筹学》 第八章 习题答案.pdf
- 《管理运筹学》习题3解答.doc
- 《管理运筹学》复习题及参考答案.doc
- 《管理运筹学》复习题及参考答案管.doc
- 《精通VerilogHDL:IC设计核心技术实例详解》书后习题以及答案.doc
- 《精馏》课后选做题-配有答案.pdf
- 《系统工程》复习题及答案.docx
- 《系统工程》第四版习题解答.doc
- 《线性代数》第3章习题解答(rr).doc
- 《组织行为学》第三版 (张德 着) 课后习题答案 高等教育出版社.pdf
- 《经济学原理》练习题、答案.doc
- 《经济学基础》(精要版)第6版1-3章课后习题详解.docx
- 《经济学基础》各章习题及参考答案.doc
- 《结构力学》第5章习题参考答案.doc
- 《结构力学》第6章习题参考答案.doc
- 《结构力学》课后习题答案.doc
- 《结构力学习题集》(下)-结构的动力计算习题及答案.doc
- 《结构力学习题集》(下)-结构的极限荷载习题及答案.doc