- 280.50 KB
- 2022-04-29 14:07:19 发布
- 1、本文档共5页,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,可选择认领,认领后既往收益都归您。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细先通过免费阅读内容等途径辨别内容交易风险。如存在严重挂羊头卖狗肉之情形,可联系本站下载客服投诉处理。
- 文档侵权举报电话:19940600175。
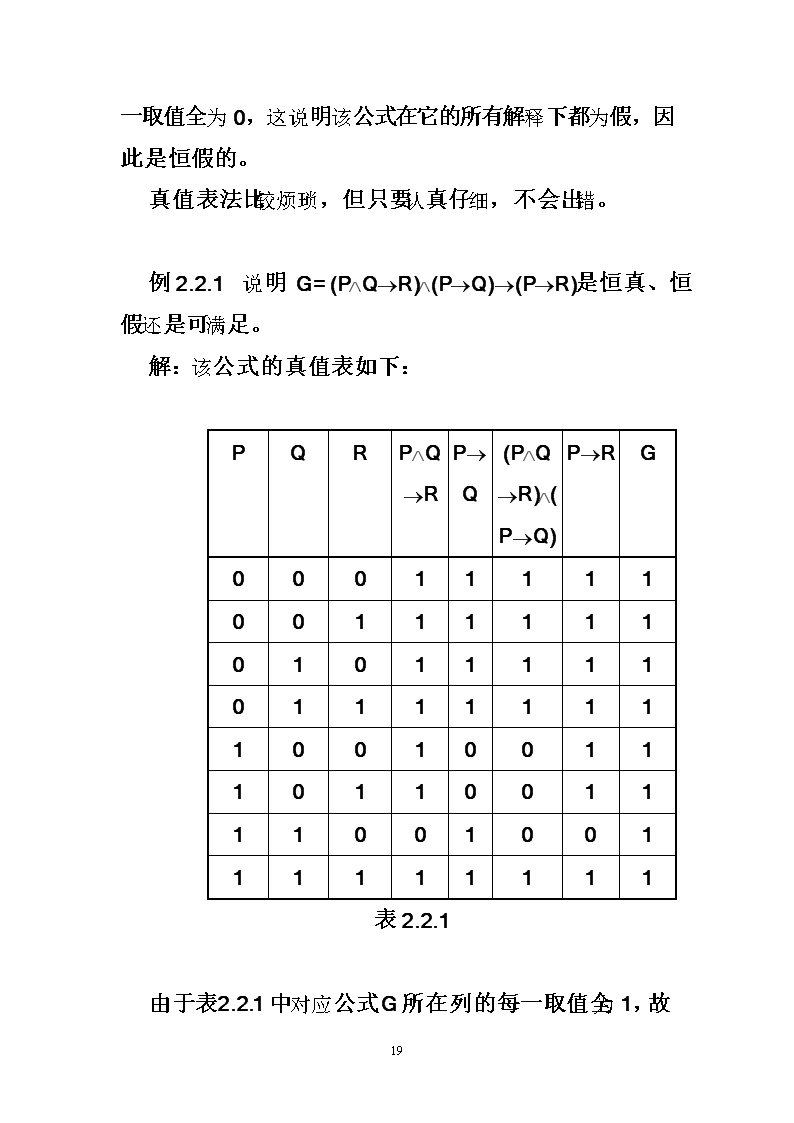
'第二章命题逻辑§2.2主要解题方法2.2.1证明命题公式恒真或恒假主要有如下方法:方法一.真值表方法。即列出公式的真值表,若表中对应公式所在列的每一取值全为1,这说明该公式在它的所有解释下都是真,因此是恒真的;若表中对应54
公式所在列的每一取值全为0,这说明该公式在它的所有解释下都为假,因此是恒假的。真值表法比较烦琐,但只要认真仔细,不会出错。例2.2.1说明G=(PÙQ®R)Ù(P®Q)®(P®R)是恒真、恒假还是可满足。解:该公式的真值表如下:PQRPÙQ®RP®Q(PÙQ®R)Ù(P®Q)P®RG0001111100111111010111110111111110010011101100111100100111111111表2.2.1由于表2.2.1中对应公式G所在列的每一取值全为1,故54
G恒真。方法二.以基本等价式为基础,通过反复对一个公式的等价代换,使之最后转化为一个恒真式或恒假式,从而实现公式恒真或恒假的证明。例2.2.2说明G=((P®R)ÚØR)®(Ø(Q®P)ÙP)是恒真、恒假还是可满足。解:由(P®R)ÚØR=ØPÚRÚØR=1,以及Ø(Q®P)ÙP=Ø(ØQÚP)ÙP=QÙØPÙP=0知,((P®R)ÚØR)®(Ø(Q®P)ÙP)=0,故G恒假。方法三.设命题公式G含n个原子,若求得G的主析取范式包含所有2n个极小项,则G是恒真的;若求得G的主合取范式包含所有2n个极大项,则G是恒假的。方法四.对任给要判定的命题公式G,设其中有原子P1,P2,…,Pn,令P1取1值,求G的真值,或为1,或为0,或成为新公式G1且其中只有原子P2,…,Pn,再令P1取0值,求G真值,如此继续,到最终只含0或1为止,若最终结果全为1,则公式G恒真,若最终结果全为0,则公式G恒假,若最终结果有1,有0,则是可满足的。例子参见书54
中例2.4.3。方法五.注意到公式G蕴涵公式H的充要条件是:公式G®H是恒真的;公式G,H等价的充要条件是:公式G«H是恒真的,因此,如果待考查公式是G®H型的,可将证明G®H是恒真的转化为证明G蕴涵H;如果待考查公式是G«H型的,可将证明G«H是恒真的转化为证明G和H彼此相蕴涵。例2.2.3证明G=(P®R)®((Q®R)®((PÚQ)®R))恒真。证明:要证明(P®R)®((Q®R)®((PÚQ)®R))恒真,只需证明(P®R)Þ((Q®R)®((PÚQ)®R))。我们使用形式演绎法。(1)P®R规则1(2)Q®R附加前提(3)ØPÚR规则2,根据(1)(4)ØQÚR规则2,根据(2)(5)(ØPÚR)Ù(ØQÚR)规则2,根据(3)、(4)(6)(ØPÙØQ)ÚR规则2,根据(5)(7)Ø(PÚQ)ÚR规则2,根据(6)(8)(PÚQ)®R规则2,根据(7)54
(9)(Q®R)®((PÚQ)®R)规则3,根据(2)、(8)2.2.2公式蕴涵的证明方法主要有如下方法:给出两个公式A,B,证明A蕴涵B,我们有如下几种方法:方法一.真值表法。将公式A和公式B同列在一张真值表中,扫描公式A所对应的列,验证该列真值为1的每一项,它所在行上相应公式B所对应列上的每一项必为1(真),则公式A蕴涵B。例2.2.4设A=(PÙQ®R)Ù(P®Q),B=(P®R),证明:AÞB。证明:PQRPÙQ®RP®QAB0001111001111101011110111111100100154
101100111001001111111表2.2.2由表2.2.2可以看出,使A为真的解释均使B亦为真,因此,AÞB。方法二.证明A®B是恒真公式。由例2.2.1知,(PÙQ®R)Ù(P®Q)®(P®R)恒真,因此,立即可得到例2.2.4中的结论:(PÙQ®R)Ù(P®Q)Þ(P®R),即AÞB。例2.2.5设A、B和C为命题公式,且AÞB。请分别阐述(肯定或否定)下列关系式的正确性。(1)(AÙC)Þ(BÙC);(2)(A®C)Þ(B®C)。解:由AÞB知,A®B是恒真公式,故A=1时,B不可能为0。真值表如下:ABCA®B(AÙC)®(BÙC)(A®C)®54
(B®C)000111001111010110011111110111111111表2.2.3从真值表可以看出,(AÙC)®(BÙC)是恒真公式,所以,(A®C)Þ(B®C)(AÙC)Þ(BÙC)正确;(A®C)®(B®C)不是恒真公式,所以,(A®C)Þ(B®C)不正确。例2.2.6设A=(R®P)®Q,B=P®Q,证明A蕴涵B。证明:我们来证明A®B恒真。((R®P)®Q)®(P®Q)=Ø(Ø(ØRÚP)ÚQ)Ú(ØPÚQ)=((ØRÚP)ÙØQ)Ú(ØPÚQ)=(ØRÙØQ)Ú(PÙØQ)ÚØ(PÙØQ)=154
方法三.利用一些基本等价式及蕴涵式进行推导。对于例2.2.6,由基本等价式可得:A=(R®P)®Q=Ø(ØRÚP)ÚQ=(RÙØP)ÚQ=(RÚQ)Ù(ØPÚQ)=(RÚQ)Ù(P®Q)由教材中基本蕴涵式2.PÙQÞQ可知,(RÚQ)Ù(P®Q)Þ(P®Q),即A蕴涵B。方法四.任取解释I,若I满足A,往证I满足B。例2.2.7设A=P®Q,B=(R®Q)®((PÚR)®Q),证明A蕴涵B。证明:任取解释I,若I满足A,则有如下两种情况:(1)在解释I下,P为假,这时,B等价于(R®Q)®(R®Q),因此,I亦满足B。(2)在解释I下,P为真,Q为真,所以,PÚR®Q为真,故B为真,即,I满足B。综上,I满足B,因此,A蕴涵B。方法五.反证法,设结论假,往证前提假。54
对于例2.2.6,证明(R®P)®Q蕴涵P®Q,若使用方法三,是很烦琐的,而使用方法四,就很简单。假设存在解释I使P®Q为假,则只有一种情形,P在I下为真,且Q在I下为假,这时R®P在I下为真,故I弄假(R®P)®Q。因此,(R®P)®Q蕴涵P®Q。方法六.分别将公式A和公式B转化为它们各自的主析取范式或主合取范式。若公式A的主析取范式所包含的所有极小项也包含在公式B的主析取范式中;或者,公式B的主合取范式中所包含的极大项均包含在公式A的主合取范式中,则公式A蕴涵公式B。使用这种方法需要注意,当公式A和公式B中包含的原子不完全相同时,在求两公式的极小项或极大项时,要考虑该两公式包含命题原子的并集中的所有原子。在例2.2.6中,A和B的主析取范式分别为:A=(ØPÙØQÙR)Ú(ØPÙQÙØR)Ú(ØPÙQÙR)Ú(PÙQÙØR)Ú(PÙQÙR),B=(ØPÙØQÙØR)Ú(ØPÙØQÙR)Ú(ØPÙQÙØR)Ú(ØPÙQÙR)Ú(PÙQÙØR)Ú(PÙQÙR),可见,AÞB。A和B的主合取范式分别为:A=(PÚQÚR)Ù(ØPÚQÚR)Ù(ØPÚQÚØR),54
B=(ØPÚQÚR)Ù(ØPÚQÚØR)可见,AÞB。另外若给出前提集合S={G1,…,Gk},公式G,证明SÞG有如下两种方法:1.G1Ù…ÙGkÞG2.形式演绎法:根据一些基本等价式和基本蕴涵式,从S出发,演绎出G。教材中已经给出了这方面的例子,在此不再赘述。2.2.3求主合取范式和主析取范式1.极小项与极大项的性质以3个原子为例,则对应极小项和极大项的表为:PQR极小项极大项000m0=ØPÙØQÙØRM0=PÚQÚR001m1=ØPÙØQÙRM1=PÚQÚØR010m2=ØPÙQÙØRM2=PÚØQÚR011m3=ØPÙQÙRM3=PÚØQÚØR100m4=PÙØQÙØRM4=ØPÚQÚR54
101m5=PÙØQÙRM5=ØPÚQÚØR110m6=PÙQÙØRM6=ØPÚØQÚR111m7=PÙQÙRM7=ØPÚØQÚØR表2.2.4由表2.2.4可知,对n个命题原子P1,…,Pn,极小项有如下性质:(1)n个命题原子P1,…,Pn有个不同的解释,每个解释对应P1,…,Pn的一个极小项。(2)对P1,…,Pn的任意一个极小项m,有且只有一个解释使m取1值,若使极小项取1的解释对应的二进制数为i,则m记为mi,于是关于P1,…,Pn的全部极小项为m0,m1,…,。(3)任意两个不同的极小项的合取式恒假:miÙmj=0,i≠j。(4)所有极小项的析取式恒真:=1。极大项有如下性质:(1)n个命题原子P1,…,Pn有个不同的解释,每个解释对应P1,…,Pn的一个极大项。(2)对P1,…,Pn的任意一个极大项M,有且只有一个解释使M取0值,若使极大项取0的解释对应的二进制54
数为i,则M记为Mi,于是关于P1,…,Pn的全部极大项为M0,M1,…,。(3)任意两个不同的极大项的析取式恒真:MiÚMj=1,i≠j。(4)所有极大项的合取式恒假:=0。2.主合取范式与主析取范式之间的关系由极小项和极大项的定义可知,二者有如下关系:mi=ØMi,Mi=Ømi由此可知,若PÚQÚR为一公式G的主合取范式,则G=ØØG=ØØM0=Ø(M1ÙM2Ù…ÙM6)=ØM1ÚØM2Ú…ÚØM6=m1Úm2Ú…Úm6为G的主析取范式。若(ØPÙQ)Ú(ØPÙØQ)Ú(PÙQ)为一公式H的主析取范式,则H=ØØH=ØØ((ØPÙQ)Ú(ØPÙØ54
Q)Ú(PÙQ))=Ø(Ø(m0Úm1Úm3))=Ø(m2)=M2=ØPÚQ为H的主合取范式。一般地,若公式A中含n个命题原子,且A的主析取范式中含有k个极小项:,则ØA的主析取范式中必含有其余的-k个极小项,不妨设为:,即ØA=。因此,A=ØØA=Ø()==。由此可知,从一公式A的主析取范式求其主合取范式的步骤如下:(1)求出A的主析取范式中没有包含的所有极小项。(2)求出与(1)中极小项下标相同的极大项。(3)将(2)求出的所有极大项合取起来,即得A的主合取范式。类似地,从一公式A的主合取范式求其主析取范式的步骤为:54
(1)求出A的主合取范式中没有包含的所有极大项。(2)求出与(1)中极大项下标相同的极小项。(3)将(2)求出的所有极小项析取起来,即得A的主析取范式。3.求主合取范式和主析取范式的方法方法一.真值表法。主析取范式恰好是使得公式为真的解释所对应的极小项的析取组成,主合取范式恰好是使得公式为假的解释所对应的极大项的合取组成。方法二.公式推导法。设命题公式G中所有不同原子为P1,…,Pn,则G的主析取范式的求法如下:(a)将公式G化为析取范式。(b)删去析取范式中所有恒假的短语。(c)用等幂律将短语中重复出现的同一文字化简为一次出现,如,PÙP=P。(d)对于所有不是关于P1,…,Pn的极小项的短语使用同一律,补进短语中未出现的所有命题原子,并使用分配律展开,即,如果短语Gi’不是关于P1,…,Pn的极小项,则Gi’中必然缺少原子,不妨设为Pj1,…,Pjk,于是Gi’=Gi’Ù(Pj1ÚØPj1)Ù…Ù(PjkÚØPjk)54
=这样,就将非极小项Gi’化成了一些极小项之析取。将相同的短语的多次出现化为一次出现,就得到了给定公式的主析取范式。主合取范式的求法类似,留给读者作为练习。由上面讨论可知,只要求出一种范式,可立即得到另外一种范式。例2.2.8求公式G=P→(Q→R)的主析取范式与主合取范式。解:(1)使用真值表法。见表2.2.5。PQRP→(Q→R)00010011010101111001101111001111表2.2.554
根据真值表中使得公式为真的解释,所对应的极小项的析取即为其主析取范式:G=(ØPÙØQÙØR)Ú(ØPÙØQÙR)Ú(ØPÙQÙØR)Ú(ØPÙQÙR)Ú(PÙØQÙØR)Ú(PÙØQÙR)Ú(PÙQÙR)=m0Úm1Úm2Úm3Úm4Úm5Úm7根据真值表中使得公式为假的解释,所对应的极大项的合取即为其主合取范式:G=ØPÚØQÚR=M6(2)公式推导法G=P→(Q→R)=ØPÚØQÚR=(ØPÙ(QÚØQ)Ù(RÚØR))Ú(ØQÙ(PÚØP)Ù(RÚØR))Ú(RÙ(PÚØP)Ù(QÚØQ))=(ØPÙØQÙØR)Ú(ØPÙØQÙR)Ú(ØPÙQÙØR)Ú(ØPÙQÙR)Ú(PÙØQÙØR)Ú(PÙQÙR)=m0Úm1Úm2Úm3Úm4Úm5Úm7G=P→(Q→R)=ØPÚØQÚR=M654
4.主合取范式与主析取范式的应用(1)由2.2.1可知,利用主合取范式与主析取范式可求解判定问题。(2)证明等价式成立。由于任意公式的主范式是唯一的,所以可以分别求出两个给定的公式的主范式,若二者主范式相同,则给定的两公式是等价的,否则,给定的两公式不等价。例2.2.9判断P→(Q→R)与(PÚQ)→R是否等价。证明:我们利用求主合取范式的方法来判断。由例2.2.8知,P→(Q→R)的主合取范式为:M6。下面求(PÚQ)→R的主合取范式。(PÚQ)→R=Ø(PÚQ)ÚR=(ØPÙØQ)ÚR=(ØPÚR)Ù(ØQÚR)=(ØPÚ(QÙØQ)ÚR)Ù((PÙØP)ÚØQÚR)=(ØPÚQÚR)Ù(ØPÚØQÚR)Ù(PÚØQÚR)=M2ÙM4ÙM654
二者的主合取范式不相同,因此,这两个公式不等价。2.2.4联结词的转化和全功能集关于联结词的转化和全功能集方面一般有如下题型:(1)要求只用几个联结词表示某个命题公式,见例2.2.10。(2)给出一个新的联结词的定义,要求证明其是全功能集,并用其表示某个命题公式。这种题目的做法如下:由于不难证明出{Ø,Ù},{Ø,Ú},{Ø,→},{},{¯}都是全功能联结词集合,因此,若要证明新定义的联结词是全功能集,只需证明上面某个全功能集合(比如{Ø,Ù})中的每个联结词(如,Ø和Ù)都可以用新联结词表示。若想用其表示某个命题公式,可以先将基本联结词(Ø,Ù,Ú)用给定的新联结词表示,然后按要求把原命题公式转化成用新联结词表示的形式。见例2.2.11。(3)证明一个联结词集合不是全功能集。一般用归纳法,证明在有限步内,用这个联结词结合不可能表示所有的命题。见例2.2.12。应该说明的是,寻求最少联结词的全功能联结词集合,主要不是个理论问题,而是为了满足工程实践的需要。但是,一般情况下,为了不至于因为联结词54
的减少而使得公式的形式变得复杂,我们仍常采用“Ø,Ù,Ú,→,«”这5个联结词。例2.2.10将公式(P→(QÚØR))Ù(ØPÙQ)用仅含联结词Ø和Ú的公式等价表示。解:(P→(QÚØR))Ù(ØPÙQ)=(ØPÚ(QÚØR))Ù(ØPÙQ)=(ØPÙ(ØPÙQ))Ú((QÚØR)Ù(ØPÙQ))=(ØPÙQ)Ú(QÙ(ØPÙQ))Ú(ØRÙ(ØPÙQ))=(ØPÙQ)Ú(ØPÙQ)Ú((ØPÙQ)ÙØR)=ØPÙQ=Ø(PÚØQ)例2.2.11定义三元联结词如表2.2.6。e1e2e3f(e1,e2,e3)00010011010054
01101001101111011110表2.2.6三元联结词f(e1,e2,e3)的真值表(1)试证明{f}是完备的,即,联结词集合{Ø,Ù}或{Ø,Ú}可由该联结词表示。(2)用该联结词表示公式:(P→R)ÙQ。(1)证明:因为ØP=f(P,P,P),PÚQ=f(ØP,ØP,ØQ),所以联结词集合{Ø,Ú}可由该三元联结词f表示。而联结词集合{Ø,Ú}是完备的,因此,{f}是完备的。(2)解:因为PÚQ=f(ØP,ØP,ØQ),所以P→Q=ØPÚQ=f(P,P,ØQ).又由PÙQ=Ø(ØPÚØQ)=Ø(ØQÚØP)=Øf(P,P,Q)=Øf(Q,Q,P).因此54
(P→R)ÙQ=f(P,P,ØR)ÙQ=Øf(Q,Q,f(P,P,ØR))=Øf(Q,Q,f(P,P,f(R,R,R)))=f(f(Q,Q,f(P,P,f(R,R,R))),f(Q,Q,f(P,P,f(R,R,R))),f(Q,Q,f(P,P,f(R,R,R))))。例2.2.12{Ù,→}是否是联结词的全功能集合?证明你的结论。在证明此题之前,我们先直观分析一下。考虑Ù和→这两个联结词的特点:当一个命题公式中只含有联结词Ù和→时,则当公式中出现的所有命题原子都取真值1时,公式也必然取真值1。这就是说,仅含Ù和→的公式不能表示所有的命题公式,比如恒假式:AÙØA。因此,联结词集合{Ù,→}不是全功能集。证明:下面证明{Ù,→}不是联结词的全功能集。对公式中出现的联结词个数使用数学归纳法来证明下面的结论:当一个命题公式中只含有联结词Ù和→时,则当公式中出现的所有命题原子都取真值1时,公式也必然取真值1。n=0时,即公式中不含任何联结词时,公式为原子,结论显然。假设n≤k时,命题成立,即,如果一个公式中含有n54
个联结词Ù,→,则当公式的所有原子真值取1时,公式也取真值1。当n=k+1时,设任一含k+1个联结词的公式为A,则存在公式B和C,使得:A=B→C或A=BÙC,且B和C中的联结词个数均≤k。由归纳假设知,当所有原子取真值1时,B和C在该解释下的真值均为1,因此,A在该解释下的真值亦为1。归纳完成。由该结论知,如果一个命题公式中只含有联结词Ù和→,那么至少存在一个解释满足该公式。因此,只含有联结词Ù和→的公式肯定不能表示恒假公式。所以,{Ù,→}不是联结词的全功能集。2.2.5综合应用题综合题主要是先符号化,再使用上面的知识进行联结词的转化、或求主合取范式、主析取范式、利用基本等价式化简、或进行逻辑推理来论证或做逻辑判断等。例2.2.13一个排队线路,输入为A,B,C,其输出分别为FA,FB,FC。在同一时间内只能有一个信号通过。如果同54
时有两个或两个以上信号通过时,则按A,B,C的顺序输出。例如,A,B,C同时输入时,只能A有输出。写出FA,FB,FC的逻辑表达式,并化成全功能集{¯}中的表达式。解:先将已知事实中的各简单命题符号化,设:P:A输入;Q:B输入;R:C输入。然后根据已知条件,写出FA,FB,FC的真值表如表2.2.7。PQRFAFBFC000000001001010010011010100100101100110100111100表2.2.7于是,FA=(PÙØQÙØR)Ú(PÙØQÙR)Ú(PÙQÙØR)54
Ú(PÙQÙR)=((PÙØQ)Ù(ØRÚR))Ú((PÙQÙ(ØRÚR))=(PÙØQ)Ú(PÙQ)=PÙ(ØQÚQ)=P=ØØ(PÚP)=Ø(P¯P)=Ø((P¯P)Ú(P¯P))=(P¯P)¯(P¯P).FB=(ØPÙQÙØR)Ú(ØPÙQÙR)=(ØPÙQ)Ù(ØRÚR)=ØPÙQ=ØØ(ØPÙQ)=Ø(PÚØQ)=P¯ØQ=P¯(Q¯Q)FC=ØPÙØQÙR=Ø(PÚQÚØR)=(PÚQ)¯(ØR)=(ØØ(PÚQ))¯(ØR)=(Ø(P¯Q))¯(ØR)=((P¯Q)¯(P¯Q))¯(R¯R)54
例2.2.14一一个公安人员审查一件盗窃案,已知的事实如下:(1)A或B盗窃了x(2)若A盗窃了x,则作案时间不能发生在午夜前(3)若B证词正确,则在午夜时屋里灯光未灭(4)若B证词不正确,则作案时间发生在午夜前(5)午夜时屋里灯光灭了(6)A并不富裕试用演绎法找出盗窃犯。解:先将已知事实中的各简单命题符号化,设:P:A盗窃了xQ:B盗窃了xR:作案时间发生在午夜前S:B证词正确T:在午夜时屋里灯光未灭U:A并不富裕再将各前提写出:G1:P∨QG2:P→RG3:S→TG4::S→RG5:TG6:U演绎过程为:(1)S→T (规则1)54
(2)T(规则1)(3)S(规则2)(4)S→R(规则1)(5)R(规则2)(6)P→R(规则1)(7)P(规则2)(8)P∨Q(规则1)(9)Q(规则2)因此,是B盗窃了x。例2.2.15一甲、乙、丙、丁四个人有且仅有两个人参加围棋优胜比赛。关于谁参加比赛,下面四种判断都是正确的:(1)甲和乙只有一人参加;(2)丙参加,丁必参加;(3)乙或丁至多参加一人;(4)丁不参加,甲也不会参加。请推断出哪两个人参加了围棋比赛。解:先将已知事实中的各简单命题符号化,设:P:甲参加了比赛;Q:乙参加了比赛;R:丙参加了比赛;54
S:丁参加了比赛.依已知条件(1)--(4)有:(1)(ØPÙQ)Ú(PÙØQ)(2)R→S(3)Ø(QÙS)(4)ØS→ØP将(1)-(4)式合取起来有:((ØPÙQ)Ú(PÙØQ))Ù(R→S)ÙØ(QÙS)Ù(ØS→ØP)=((ØPÙQ)Ú(PÙØQ))Ù(ØRÚS)Ù(ØQÚØS)Ù(SÚØP)=(PÙØQÙØRÙS)Ú(PÙØQÙS)Ú(ØPÙQÙØRÙØS)根据已知,甲、乙、丙、丁四个人有且仅有两个人参加比赛,知,ØPÙQÙØRÙØS为假,所以只有(PÙØQÙØRÙS)Ú(PÙØQÙS)为真,即甲和丁参加了比赛。54
§2.3第二章习题解答2.3.1习题2.1解答1.设P是命题“天下雪”;Q是命题“我上街”;R是命题“我有时间”。(1)用逻辑符号写出以下命题:a.如天不下雪并且我有时间,那么我上街。b.我去上街,仅当我有时间。c.天不下雪。d.天正在下雪,我也没去上街。解:a可表示为:(ØPÙR)®Q;b可表示为:Q®R;c可表示为:ØP;d可表示为:PÙØQ。(2)对下述命题用中文写出语句。a.Q«(RÙØP)b.RÙQc.(Q®R)Ù(R®Q)d.Ø(RÚQ)解:a为:我上街当且仅当我有时间并且天不下雪;b为:我有时间并且上街了;c为:我上街了当且仅当我有时间;d为:我每时间又没上街。2.说出下述每一命题的逆命题和逆否命题:(1)如果天下雨,我将不去。(2)仅当你去我将逗留。(3)如果n是大于2的正整数,则方程xn+yn=zn无正整数解。(4)如果我不获得更多帮助,我不能完成这个任务。解:54
(1)逆命题为:如果我不去,那么天下雨;逆否命题为:如果我去,那么天不下雨。(2)逆命题为:仅当我将逗留你去;逆否命题为:你不去我将不逗留。(3)逆命题为:如果方程xn+yn=zn无正整数解,则n是大于2的正整数;逆否命题为:如果方程xn+yn=zn有正整数解,则n是不大于2的正整数。(4)逆命题为:我不能完成这个任务,因为我没有获得更多帮助。逆否命题:如果我完成了任务,则我获得了更多帮助。3.给P和Q指派真值1,给R和S指派真值0,求出下面命题的真值:a)(PÙ(QÙR))ÚØ((PÚQ)Ù(RÚS))b)(Ø(PÙQ)ÚØR)Ú(((ØPÙQ)ÚØR)ÙS)c)(Ø(PÙQ)ÚØR)Ú((Q«ØP)®(RÚØS))d)(PÚ(Q®(RÙØP)))«(QÚØS)解:a)令G=(PÙ(QÙR))ÚØ((PÚQ)Ù(RÚS))则:TI(G)=(1Ù(1Ù0))ÚØ((1Ú1)Ù(0Ú0))=0ÚØ0=1b)令G=(Ø(PÙQ)ÚØR)Ú(((ØPÙQ)ÚØR)ÙS)则:TI(G)=(Ø(1Ù1)ÚØ0)Ú(((Ø1Ù1)ÚØ0)Ù0)=1Ú0=1c)令G=(Ø(PÙQ)ÚØR)Ú((Q«ØP)®(RÚØS))=(Ø(PÙQ)ÚØR)Ú(Ø((ØQÚØP)Ù(PÚQ))Ú(RÚØS))=(ØPÚØQÚØR)Ú((QÙP)Ú(ØPÚØQ)Ú(RÚØS))则:TI(G)=(Ø1ÚØ1ÚØ0)Ú((1Ù1)Ú(Ø1ÚØ1)Ú(0ÚØ0))=1Ú1=1d)令G=(PÚ(Q®(RÙØP)))«(QÚØS)=(PÚ(Q®(RÙØP)))«(QÚØS)=(PÚ(ØQÚ(RÙØP)))«(QÚØS)=(Ø(PÚ(ØQÚ(RÙØP)))Ú(QÚØS))Ù(Ø(QÚØS)Ú(PÚ(ØQÚ(RÙØP))))=(ØPÙ(QÙ(ØRÚP)))Ú(QÚØS))Ù((ØQÙS)Ú(PÚ(ØQÚ(RÙØP))))TI(G)=(Ø1Ù(1Ù(Ø0Ú1)))Ú(1ÚØ0))Ù((Ø1Ù0)Ú(1Ú(Ø1Ú(0ÙØ1))))=1Ù1=12.3.2习题2.1解答1.构成下列公式的真值表:(1)QÙ(P®Q)®P(2)Ø(PÚQÙR)«(PÚQ)Ù(PÚR)(3)(PÚQ®QÙR)®PÙØR(4)((ØP®PÙØQ)®R)ÙQÚØR解:(1)设G=QÙ(P®Q)®P,其真值表如下:PQG00101054
101111(2)设G=Ø(PÚQÙR)«(PÚQ)Ù(PÚR),其真值表如下:PQRGPQRG00001001001010100100110101101110(3)设G=(PÚQ®QÙR)®PÙØR,其真值表如下:PQRGPQRG00001001001010110101110101101110(4)设G=((ØP®PÙØQ)®R)ÙQÚØR,其真值表如下:PQRGPQRG000110010010101001011101011111112.指出下列公式哪些是恒真的哪些是恒假的:(1)PÙ(P®Q)®Q(2)(P®Q)®(ØPÚQ)(3)(P®Q)Ù(Q®R)®(P®R)(4)(P«Q)«(PÙQÚØPÙØQ)解:(1)是恒真的,(2)是恒真的,(3)是恒真的,(4)是可满足的。3.对P和Q的所有值,证明P®Q与ØPÚQ有同样的真值。证明(P®Q)«(ØPÚQ)是恒真的。解:对P®Q的任意解释I,若I使P®Q为真,则I使P为假或P和Q同时为真,若I使P为假,则使ØP,此时ØPÚQ为真,若I使P和Q同时为真,则Q为真,此时ØPÚQ为真,也就是说P®Q为真时ØPÚQ为真。若I使P®Q为假,则I使P为真Q为假,此时ØPÚQ为假,也就是说P®Q为假时ØPÚQ为假。综上知P®Q与ØPÚQ同真同假,由定义知(P®Q)«(ØPÚQ)是恒真的。4.判断下列公式是恒真?恒假?可满足?a)(P®(QÙR))Ù(ØP®(ØQÙØR));b)P®(PÙ(Q®P));c)(Q®P)Ù(ØPÙQ);d)(ØPÚØQ)®(P«ØQ)。解:(1)设G=(P®(QÙR))Ù(ØP®(ØQÙØR))=(ØPÚ(QÙR))Ù(PÚ(ØQÙØR))54
=(((ØPÚ(QÙR))ÙP)Ú((ØPÚ(QÙR))ÙØQÙØR)=((ØPÙP)Ú(PÙQÙR))Ú((ØPÚ(QÙR))ÙØQÙØR)=((ØPÙP)Ú(PÙQÙR))Ú((ØPÚQ)Ù(ØPÚR)ÙØQÙØR)=((ØPÙP)Ú(PÙQÙR))Ú(((ØPÚQ)ÙØQ)Ù((ØPÚR)ÙØR))=(PÙQÙR)Ú(ØPÙØQÙØR),其真值表如下:PQRGPQRG00011000001010100100110001101111因此G是可满足的。(2)设G=P®(PÙ(Q®P))=ØPÚ(PÙ(ØQÚP))=ØPÚP=T其真值表如下:PQG001011101111因此G是恒真的。(3)G=(Q®P)Ù(ØPÙQ)=(ØQÚP)Ù(ØPÙQ)=Ø(ØPÙQ)Ù(ØPÙQ)=F其真值表如下:PQG000010100110因此G是恒假的。(4)G=(ØPÚØQ)®(P«ØQ)=(PÙQ)Ú((P®ØQ)Ù(ØQ®P))=(PÙQ)Ú((ØPÚØQ)Ù(QÚP))=(PÙQ)Ú(ØPÙQ)Ú(PÙØQ)其真值表如下:PQG00001110154
111因此G是可满足的。2.3.3习题2.3解答1.证明下面的等价式:(1)(ØPÙ(ØQÙR))Ú(QÙR)Ú(PÙR)=R(2)P®(Q®P)=ØP®(P®Q)(3)P®(QÚR)=(P®Q)Ú(P®R)(4)(P®Q)Ù(R®Q)=(PÚR)®Q(1)证明:(ØPÙ(ØQÙR))Ú(QÙR)Ú(PÙR)=(((ØPÙ(ØQÙR))ÚQ)Ù((ØPÙ(ØQÙR))ÚR))Ú(PÙR)=((((ØPÚQ)Ù(RÚQ))Ù((ØPÚR)ÙR))Ú(PÙR)=((ØPÚQ)Ù(RÚQ)ÙR)Ú(PÙR)=((ØPÚQ)ÙR)Ú(PÙR)=(ØPÙR)Ú(QÙR)Ú(PÙR)=RÙ(ØPÚP)Ú(QÙR)=R得证。(2)证明:左边=P®(Q®P)=ØPÚ(ØQÚP)=ØPÚØQÚP=PÚØPÚØQ=T右边=ØP®(P®Q)=PÚØPÚQ=T可有:左边=右边,得证(3)证明:左边=ØPÚQÚR右边=ØPÚQÚØPÚR=ØPÚQÚR可有:左边=右边,得证(4)证明:左边=(ØPÚQ)Ù(ØRÚQ)=(ØPÙØR)ÚQ=Ø(PÚR)ÚQ=(PÚR)®Q=右边得证2设S={G1,…,Gn}是命题公式集合。试求出在不增加新原子的情况下从S出发演绎出的所有命题公式。提示:考虑G1Ù…ÙGn的主合取范式。解:任设一公式G’为从S出发演绎出来的公式。则可知G’为G=G1Ù…ÙGn的一个逻辑结果。而G有唯一一个与其等价的主合取范式,设为G’’。可设G’’共有m个极大项,则可以知道令G’’取1的解释使这m个极大项也取1。则从S出发的演绎出来的的所有命题公式正是从这m个极大项中任取n(0≤n≤54
m)个合取组成,共有2m个,其中包括恒真公式这里用1表示。设H为由若干极大项构成的合取公式。现在证明:1)S=>H,即G=>H。从定义出发,设有一解释I使G=G1Ù…ÙGn取1值,必使G的主合取范式也取1值。即使每一个极大项都取1值。从而使由若干极大项合取组成的公式H也取1值,则有S=>H。2)任意设公式H是S的一个逻辑结果,H是一些极大项的合取。现在要证组成H的极大项都在G的主合取范式G”中。反证法:若不然,假设H中有一个极大项mk不在G的主合取范式中。则取使mk为0的解释I,可有解释I使H取0值。而I使所有不等于mk的极大项都为1,则可有G的主合取范式G’’在I下取1值,即G在I下取1值,这与G=>H矛盾。3.证明:两个公式之间的蕴涵关系具有反身性,反对称性和传递性。证明:a)任意设一公式P,由于P®P是恒真的,则有P=>P即蕴涵关系有反身性。b)任取两个命题公式P,Q如果P=>Q并且Q=>P,则有P®Q恒真,Q®P恒真,则(P®Q)Ù(Q®P)恒真,那么有P«Q恒真,得出P=Q,所以蕴涵关系有反对称性。c)任取命题公式P,Q,R如果P=>Q,Q=>R;对于P,Q,R的任意一个解释I。如果I满足P则I也满足Q,若I满足Q则I满足R。则有I满足P时,也满足R,故有P=>R。因此蕴涵关系有传递性。4.证明:若前提集合S中的公式都是恒真的,G是从S出发的一个演绎的逻辑结果,则G必是恒真公式。证明:设S是由G1,…,Gn构成的,则G1,…,Gn是恒真的,那么G1Ù…ÙGn是恒真的,而由已知有:G1Ù…ÙGn=>G,因此由蕴涵定义有G必为恒真公式。5.设G1,…,Gn是公式。证明:从{G1,…,Gn}出发可演绎出公式G的充要条件是从{G1,…,Gn,ØG}出发可演绎出公式(RÙØR)。其中R为任意公式。证明:充分性,即{G1,…,Gn,ØG}=>(RÙØR),可有G1Ù…ÙGnÙØG=>(RÙØR),因(RÙØR)恒假,则G1Ù…ÙGnÙØG恒假。那么有Ø(G1Ù…ÙGn)ÚG恒真,即(G1Ù…ÙGn)®G恒真,则有(G1Ù…ÙGn)=>G,因此有{G1,…,Gn}蕴涵G。必要性,即已知:{G1,…,Gn}=>G,有(G1Ù…ÙGn)®G恒真,即Ø(G1Ù…ÙGn)ÚG恒真,那么对上式取非有G1Ù…ÙGnÙØG恒假,也就是(G1Ù…ÙGnÙØG)®(RÙØR)恒真,其中R为任意一个公式,则有(G1Ù…ÙGnÙØG)=>(RÙØR),即从{G1,…,Gn,ØG}出发可演绎出公式(RÙØR)。命题得证。6.证明下列蕴涵式:(1)(PÙQ)Þ(P®Q)54
证明:要证上式成立即证(PÙQ)®(P®Q)恒真,则:(PÙQ)®(P®Q)=Ø(PÙQ)Ú(ØPÚQ)=(ØPÚØQ)Ú(ØPÚQ)=ØPÚØQÚQ=T即:(PÙQ)®(P®Q)恒真命题得证。(或从PÙQÞQ,QÞ(P®Q))(2)PÞ(Q®P)证明:同a),P®(Q®P)=ØPÚ(ØQÚP)=ØPÚPÚØQ=T命题得证。(或从PÞ(ØQÚP)出发)(3)(P®(Q®R))Þ(P®Q)®(P®R)证明:(P®(Q®R))®(P®Q)®(P®R)=(PÙQÙØR)ÚØ(PÙQÙØR)=T得证。(4)P®QÞP®(PÙQ)证明:若P®(PÙQ)为假,则PÙQ为假,P为真。因而有Q为假,则P®Q为假,(后件假推出前件假等价于前件真推出后件真)得证。(5)(P®Q)®QÞPÚQ证明:(P®Q)®Q=Ø(ØPÚQ)ÚQ=(PÙØQ)ÚQ=(PÚQ)Ù(QÚØQ)=>(PÚQ)(基本蕴涵式)(6)((PÚØP)®Q)®((PÚØP)®R)Þ(Q®R)证明:若(Q®R)为假,则R为假,Q为真,则(PÚØP)®R为假,而(PÚØP)®Q为真,则有((PÚØP)®Q)®((PÚØP)®R)为假,得证。(用P®Q证明也可)(7)(Q®(PÙØP))®(R®(PÙØP))Þ(R®Q)证明:若(R®Q)为假,则Q为假,R为真,则R®(PÙØP)为假,而Q®(PÙØP)为真。有(Q®(PÙØP))®(R®(PÙØP))为假,得证。7.证明{CÚD,(CÚD)®ØH,ØH®(AÙØB),(AÙØB)®(RÚS)}共同蕴涵RÚS。证明:1)CÚD规则12)(CÚD)®ØH规则13)ØH规则2,根据1),2)4)ØH®(AÙØB)规则15)(AÙØB)规则2,根据3),4)6)(AÙØB)®(RÚS)规则154
7)RÚS规则2,根据5),6)8.证明{PÚQ,Q®R,P®M,ØM}共同蕴涵RÙ(PÚQ)。证明:1)P®M规则12)ØM®ØP规则2,根据1)3)ØM规则14)ØP规则2,根据2),3)5)PÚQ规则16)ØP®Q规则2,根据5)7)Q规则2,根据4),6)8)Q®R规则19)R规则2,根据7),8)10)RÙ(PÚQ)规则2,根据5),9)9.证明{ØPÚQ,ØQÚR,R®S}共同蕴涵P®S。证明:1)ØPÚQ规则12)P规则3(附加前提)3)Q规则2,根据1),2)4)ØQÚR规则15)R规则2,根据3),4)6)R®S规则17)S规则2,根据5),6)8)P®S规则3,根据2),7)2.3.4习题2.4解答1.试证明公式:((PÚQ)ÙØ(ØPÙ(ØQÚØR)))Ú(ØPÙØQ)Ú(ØPÙØR)是恒真公式。证明:原式=((PÚQ)ÙØ(ØPÙ(ØQÚØR)))Ú(ØPÙØQ)Ú(ØPÙØR)=((PÚQ)Ù(PÚ(QÙR)))Ú(ØPÙØQ)Ú(ØPÙØR)=((PÚQ)Ù(PÚQ)Ù(PÚR))ÚØ(PÚQ)ÚØ(PÚR)=(PÙ(QÚR))ÚØ(PÙ(QÚR))=T2.模仿主析取范式的概念,引进主合取范式的概念。并证明:对任意命题公式,存在唯一一个与其等价的主合取范式。首先引进极大项概念:定义6:设P1,…,Pn是n个不同原子,一个子句如果恰好包含所有这n个原子或其否定,且其排列顺序与P1,…,Pn的顺序一致,则称此子句为关于P1,…,Pn的一个极大项。定义7:设命题公式G中所有不同原子为P1,…,Pn,如果G的某个合取范式G’中的每一个子句,都是关于P1,…,Pn的一个极大项,则称G’为G的主合取范式。证明:(对任意命题公式,存在唯一一个与其等价的主合取范式。)54
由定理1知对于命题公式G,存在与它等价的合取范式G’,设G中的不同原子为P1,…,Pn。对于G’中的每一个子句G’i进行检查,如果G’i不是关于P1,…,Pn的极大项,则G’i必然缺少原子Pj1,…Pjk。则可以通过如下方式扩展G’iG’i=G’iÚ(Pj1ÙØPj1)Ú…Ú(PjkÙØPjk)=Mi1Ù…ÙMi2k于是将G’中的非极大项G’i化成了一些极大项的合取。对其它非极大项也做同样处理,得到等价于G的主合取范式G’’。现在证唯一性,也就是证明对任意两个关于P1,…,Pn的主合取范式,如果公式不完全相同,则G与H不等价。任意取两个命题公式G、H是关于P1,…,Pn的两个主合取范式。若G和H不完全相同。则必然存在一个极大项Mi在G’中而不在H中(或相反),则取一解释I使Mi取0值,即使公式G取0值。由定义可知I使非Mi的极大项都为1,从而有I使H取1值。所以G与H不等价。从而有对任意命题公式,存在唯一一个与其等价的主合取范式。3.证明:命题公式G是恒真的当且仅当在等价于它的合取范式中,每个子句均至少包含一个原子及其否定。证明:设公式G的合取范式为:G’=G1ÙG2Ù…ÙGn若公式G恒真,则G’恒真,即子句Gi;i=1,2,…n恒真为其充要条件。Gi恒真则其必然有一个原子和它的否定同时出现在Gi中,也就是说无论一个解释I使这个原子为1或0,Gi都取1值。若不然,假设Gi恒真,但每个原子和其否定都不同时出现在Gi中。则可以给定一个解释I,使带否定号的原子为1,不带否定号的原子为0,那么Gi在解释I下的取值为0。这与Gi恒真矛盾。因此,公式G是恒真的当且仅当在等价于它的合取范式中,每个子句均至少包含一个原子及其否定。4.试将下列公式化为析取范式和合取范式:a)PÙ(P®Q)b)Ø(PÚQ)«(PÙQ)解:a)PÙ(P®Q)=PÙ(ØPÚQ)(合取范式)=(PÙØP)Ú(PÙQ)(析取范式)=PÙQ(合取、析取范式)b)Ø(PÚQ)«(PÙQ)=(Ø(PÚQ)®(PÙQ))Ù((PÙQ)®Ø(PÚQ))=((PÚQ)Ú(PÙQ))Ù((ØPÚØQ)Ú(ØPÙØQ))=(PÚQÚ(PÙQ))Ù(ØPÚØQÚ(ØPÙØQ))=(PÚQ)Ù(ØPÚØQ)(合取范式)=((PÚQ)ÙØP)Ú((PÚQ)ÙØQ)=(ØPÙQ)Ú(PÙØQ)(析取范式)54
5.试将下列公式化为主析取范式和主合取范式:(1)P®((P®Q)ÙØ(ØQÚØP));(2)PÚ(ØP®(QÚ(ØQ®R)))。解:(1)P®((P®Q)ÙØ(ØQÚØP))=ØPÚ((ØPÚQ)ÙQÙP)=ØPÚ(QÙP)=(ØPÙ(QÚØQ))Ú(QÙP)=(ØPÙQ)Ú(ØPÙØQ)Ú(QÙP)(主析取范式)=ØPÚ(QÙP)=(ØPÚQ)Ù(ØPÚP)=ØPÚQ(主合取范式)(2)PÚ(ØP®(QÚ(ØQ®R)))=PÚ(PÚ(QÚ(QÚR)))=PÚ(PÚQÚR)=PÚQÚR(主合取范式)=(PÙ(QÚØQ)Ù(RÚØR))Ú(QÙ(PÚØP)Ù(RÚØR))Ú(RÙ(PÚØP)Ù(QÚØQ))=(PÙQÙR)Ú(PÙØQÙR)Ú(PÙQÙØR)Ú(PÙØQÙØR)Ú(QÙPÙR)Ú(QÙØPÙR)Ú(QÙPÙØR)Ú(QÙØPÙØR)Ú(RÙPÙQ)Ú(RÙØPÙQ)Ú(RÙPÙØQ)Ú(RÙØPÙØQ)=(PÙQÙR)Ú(PÙØQÙR)Ú(PÙQÙØR)Ú(PÙØQÙØR)Ú(QÙØPÙR)Ú(QÙØPÙØR)Ú(RÙØPÙØQ)=(PÙQÙR)Ú(PÙØQÙR)Ú(PÙQÙØR)Ú(PÙØQÙØR)Ú(ØPÙQÙR)Ú(ØPÙQÙØR)Ú(ØPÙØQÙR)(主析取范式)54'
您可能关注的文档
- 司法考试《卷一》模拟试题及答案每日一练(2016.2.5).doc
- 司法考试《卷一》模拟试题及答案每日一练(2016.3.24).doc
- 司法考试《卷一》模拟试题及答案每日一练(2016.8.22).doc
- 司法考试《法制史》考点模拟试题及答案每日一练(2016.2.18).doc
- 各科习题答案.doc
- 各章名词解释很多没答案.doc
- 合肥工业大学《工程图学》习题解答.pdf
- 合集:《健康评估-学习指导与习题集》:.doc
- 吉大11春学期《新视野英语(三)》复习题及答案.doc
- 吉林电子信息职业技术学院2012年《关系数据库与SQL Server 2005》习题参考答案.doc
- 同济-线性代数第五版(课后全部答案).pdf
- 同济大学《建筑混凝土结构设计》习题解答汇总2014-6-24.pdf
- 同济大学《高等数学》第3版下册答案.doc
- 同济大学《高等数学》第三版下册答案.doc
- 同济大学《高等数学》第五版下册答案 2.doc
- 同济大学推荐结构力学习题集 含答案.pdf
- 同济大学朱慈勉 结构力学 第5章习题答案.doc
- 同济大学朱慈勉 结构力学 第6章习题答案.doc