- 1.22 MB
- 2022-04-29 14:07:25 发布
- 1、本文档共5页,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,可选择认领,认领后既往收益都归您。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细先通过免费阅读内容等途径辨别内容交易风险。如存在严重挂羊头卖狗肉之情形,可联系本站下载客服投诉处理。
- 文档侵权举报电话:19940600175。
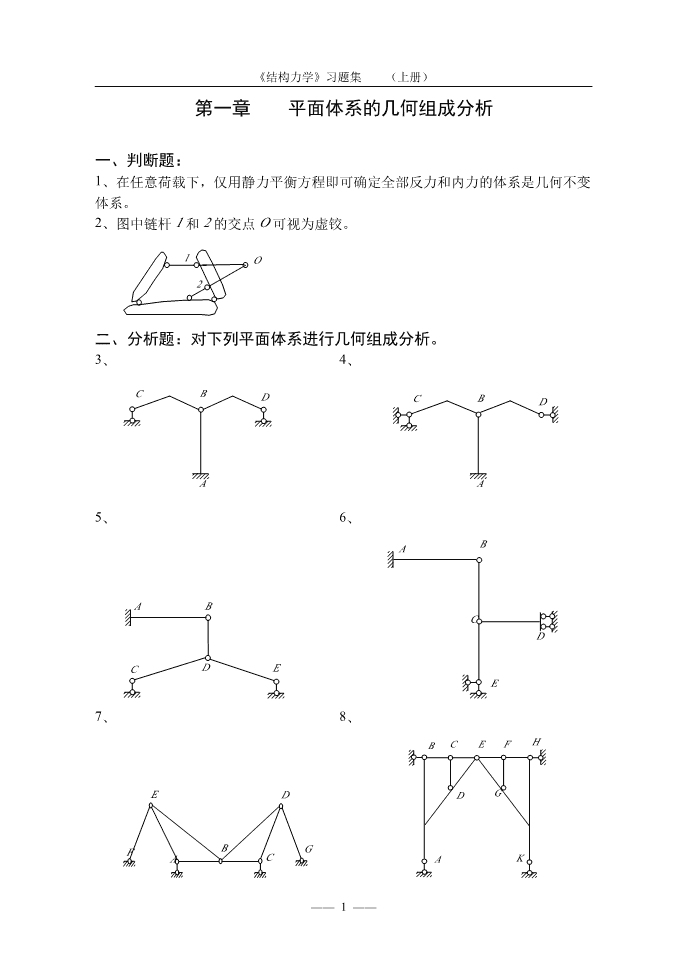
'《结构力学》习题集(上册)第一章平面体系的几何组成分析一、判断题:1、在任意荷载下,仅用静力平衡方程即可确定全部反力和内力的体系是几何不变体系。2、图中链杆1和2的交点O可视为虚铰。1O2二、分析题:对下列平面体系进行几何组成分析。3、4、CBDCBDAA5、6、BAABCDCDEE7、8、BCEFHEDDGFBGACAK——1——
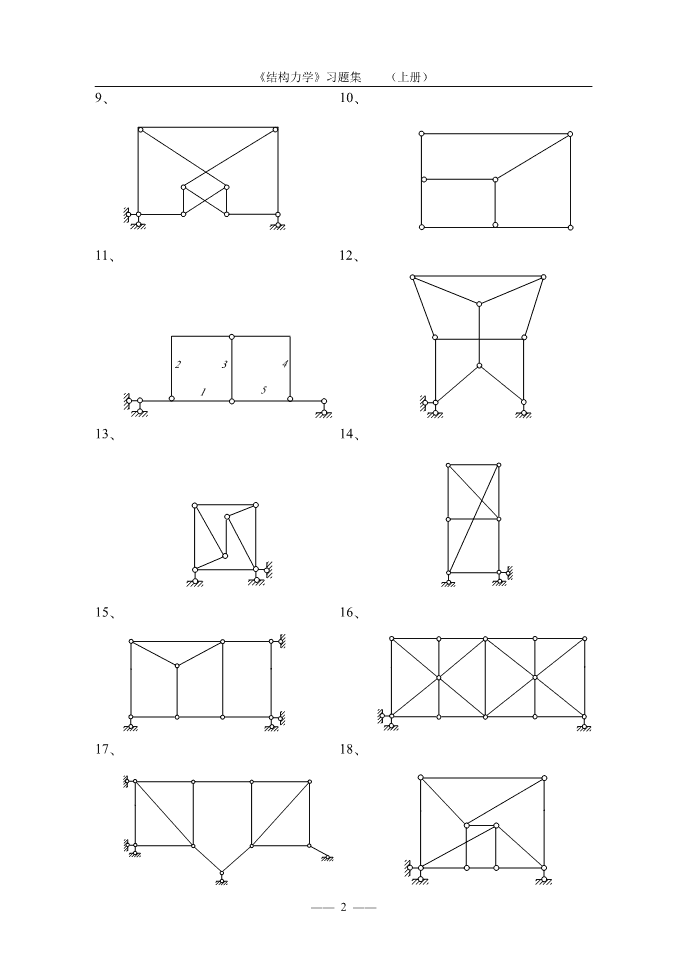
《结构力学》习题集(上册)9、10、11、12、2341513、14、15、16、17、18、——2——
《结构力学》习题集(上册)19、20、4512321、22、567845141232323、24、64512325、26、27、28、——3——
《结构力学》习题集(上册)29、30、31、32、33、ABCFDE三、在下列体系中添加支承链杆,使之成为无多余约束的几何不变体系。34、35、第二章静定结构内力计算——4——
《结构力学》习题集(上册)一、判断题:1、静定结构的全部内力及反力,只根据平衡条件求得,且解答是唯一的。2、静定结构受外界因素影响均产生内力,内力大小与杆件截面尺寸无关。3、静定结构的几何特征是几何不变且无多余约束。4、图(a)所示结构|MC|=0。PCaBCP2aaADϕaa2aaa(a)(b)5、图(b)所示结构支座A转动ϕ角,MAB=0,RC=0。6、荷载作用在静定多跨梁的附属部分时,基本部分一般内力不为零。7、图(c)所示静定结构,在竖向荷载作用下,AB是基本部分,BC是附属部分。ABC(c)8、图(d)所示结构B支座反力等于P/2(↑)。PABll(d)9、图(e)所示结构中,当改变B点链杆的方向(不通过A铰)时,对该梁的影响是轴力有变化。BA(e)10、在相同跨度及竖向荷载下,拱脚等高的三铰拱,水平推力随矢高减小而减小。11、图(f)所示桁架有9根零杆。——5——
《结构力学》习题集(上册)PPPP123ACBaaaa(f)(g)12、图(g)所示桁架有:N1=N2=N3=0。13、图(h)所示桁架DE杆的内力为零。DPaEPPaaa(h)(i)14、图(i)所示对称桁架在对称荷载作用下,其零杆共有三根。15、图(j)所示桁架共有三根零杆。P3m2mP3m3m3m(j)(k)16、图(k)所示结构的零杆有7根。17、图(l)所示结构中,CD杆的内力N1=P。PP/2P/2PPPCa1D4a4a(l)(m)18、图(m)所示桁架中,杆1的轴力为0。——6——
《结构力学》习题集(上册)二、作图题:作出下列结构的弯矩图(组合结构要计算链杆轴力)。19、20、40kN40kNP20kN/mm03a/43a/4a/2a/22m2m2m2m4m21、22、1kN/m2P2PaP2maaaaa4m2m23、24、10kN/mm=20kNm.q=20kN/m40kN1kN.m1kN.m8m4m4m4m2m2m25、26、qqh2aha2aa27、28、PP2aaa2a2aaa29、30、——7——
《结构力学》习题集(上册)PPm0aaaaa/2a/2aa/2a/231、32、q=P/aaCPP1.5aaBmB1.5aaAAaaa33、34、PlmllPll2lll35、36、40kN/mAq=4P/aCD2P3maECE20kN/m6mBABPaaD4m4maaaa37、38、——8——
《结构力学》习题集(上册)qqBlqlllAlllll39、40、qPaaaa2aa2aaa41、42、P=10kNPa3m3ma3m3maa43、44、qllPaqlll45、46、——9——
《结构力学》习题集(上册)ql23mql3m10kNl3m3m47、48、20kNmCEB2m4mD2m2mA4×2m=8m4m2m49、50、PP16kNm.a4kN4maa4m2m2m4maa51、52、10kN/m10kN/m10kN1m4m2m3m1m1m3m3m3m53、54、——10——
《结构力学》习题集(上册)2kN/maEFD3mqaC2maB2mA2a2m4m55、56、q2m2aq=2kN/ma2a2aa2m2m57、58、P10kN3maa3m4m4maaaa59、60、mP0ACD2lEFBllaaa61、62、——11——
《结构力学》习题集(上册)qPPl/2qlllll/2l/2l/263、64、qPqqalPall65、66、8kNP2mEF2kN/m2mCaD2mAa2mBPPaaaa3m1m67、68、PPPPa1lllllaaaa69、70、——12——
《结构力学》习题集(上册)P20kNm.3a6kN3m3m3m2m3ma3a71、72、10kN/m4mPa3m3maaaa73、74、10kN/m2kN/m12kN1m4m2m3m1m1m2m4m2m2m2m75、76、6kN/m20kN2m10kNm.10kN10kN5m4m13kNm2kN/m3m3m3m2m2m2m2m2m2m77、78、——13——
《结构力学》习题集(上册)PPa2a5aaaa2a三、计算题:79、计算图示半圆三铰拱K截面的内力MK,NK。已知:q=1kN/m,M=18kN·m。qMCK30°R=6mAB3m3m6m280、计算图示抛物线三铰拱K截面的内力MK,NK,拱轴方程为:y=4fx(l-x)/l.已知:P=4kN,q=1kN/m,f=8m,|ϕK|=45°.PqyKCfABx4m4m4m4m�81、图示三铰拱K截面倾角ϕ=2633′(sinϕ=0.447,cosϕ=0.894),计算K截2面内力MK,NK。y=4fx(l−x)/l,(l=16m,f=4m)20kNm.ky4mφx4m4m8m——14——
《结构力学》习题集(上册)82、计算图示半圆拱K截面弯矩。PKCRooB4560A83、计算图示桁架中杆1、2、3的内力。a3A1B22P6a84、计算图示桁架中杆1,2的内力。PAB2m12P2mCDPEF2mHG1.5m1.5m85、计算图示桁架中杆1,2的内力。PC2DPB0.707aE1a/2AF0.707aa0.707a86、计算图示桁架中杆1,2,3的内力。80kN40kN40kN140kN324m4mAB4m4m4m4m——15——
《结构力学》习题集(上册)87、计算图示桁架杆1、2的内力。a21Paaaa88、计算图示桁架杆1、2、3的内力。P1Pa3a2aaaaa89、计算图示桁架杆1、2的内力。Pa/31a/32a/3a/2a/290、计算图示桁架杆1、2的内力。a122Paaa91、计算图示桁架结构杆1、2的轴力。P1d2dddd/2d/2d——16——
《结构力学》习题集(上册)92、计算图示桁架结构杆1、2的轴力。P13P24m4m4m4m4m4m93、计算图示桁架杆1、2的轴力。21aP4a94、计算图示桁架中a杆的内力Na,d=3m。40kN10kNdaddd95、计算图示桁架杆a、b的内力。PPaba4a96、计算图示桁架杆1、2的内力。PP3m214m4m3m2m——17——
《结构力学》习题集(上册)97、计算图示桁架杆件a的内力。P4ma4m4m4m4m98、计算图示桁架杆1、2的内力。PP1aa2aaaaa99、计算图示桁架杆a、b的内力。60kN4mba4m4m3m9m100、计算图示桁架各杆轴力及反力。C3m16kNEF3mADB4m4m——18——
《结构力学》习题集(上册)101、作图示结构的M图并求杆1的轴力。P1lllllllll102、作图示结构的M图并求链杆的轴力。Pl12llll103、作图示结构的M图并求链杆的轴力。d=4m。40kNm5kNd40kNmdd104、作图示结构弯矩图。2m1m2m4m4m4m4m第三章静定结构的位移计算——19——
《结构力学》习题集(上册)一、判断题:1、虚位移原理等价于变形谐调条件,可用于求体系的位移。2、按虚力原理所建立的虚功方程等价于几何方程。3、在非荷载因素(支座移动、温度变化、材料收缩等)作用下,静定结构不产生内力,但会有位移且位移只与杆件相对刚度有关。4、求图示梁铰C左侧截面的转角时,其虚拟状态应取:M=1A.B.C;CM=1M=1C.D.C;C5、功的互等、位移互等、反力互等和位移反力互等的四个定理仅适用于线性变形体系。6、已知Mp、Mk图,用图乘法求位移的结果为:(ω1y1+ω2y2)/(EI)。ω1Mp*ω2*P=1AϕBM=1ACBy2y1Mk(a)δ(b)7、图a、b两种状态中,粱的转角ϕ与竖向位移δ间的关系为:δ=ϕ。8、图示桁架各杆EA相同,结点A和结点B的竖向位移均为零。PAPaBBaa9、图示桁架各杆EA=常数,由于荷载P是反对称性质的,故结点B的竖向位移等于零。二、计算题:10、求图示结构铰A两侧截面的相对转角ϕA,EI=常数。——20——
《结构力学》习题集(上册)qAlll/211、求图示静定梁D端的竖向位移∆DV。EI=常数,a=2m。10kN/mDaaa12、求图示结构E点的竖向位移。EI=常数。qEll/32/3ll/313、图示结构,EI=常数,M=90kN⋅m,P=30kN。求D点的竖向位移。MPACBD3m3m3m14、求图示刚架B端的竖向位移。q2EIBEIl/2Al15、求图示刚架结点C的转角和水平位移,EI=常数。qBCl/2Al16、求图示刚架中D点的竖向位移。EI=常数。——21——
《结构力学》习题集(上册)Pl/2Dll17、求图示刚架横梁中D点的竖向位移。EI=常数。qDaaa18、求图示刚架中D点的竖向位移。EI=常数。qDlll/2l/219、求图示结构A、B两截面的相对转角,EI=常数。AB2l/3PPl/3l20、求图示结构A、B两点的相对水平位移,EI=常数。PPABlll21、求图示结构B点的竖向位移,EI=常数。——22——
《结构力学》习题集(上册)AMlClBll22、图示结构充满水后,求A、B两点的相对水平位移。EI=常数,垂直纸面取1m宽,水比重近似值取10kN/m3。BAl2l23、求图示刚架C点的水平位移∆CH,各杆EI=常数。2kN/mC3m4m4m24、求图示刚架B的水平位移∆BH,各杆EI=常数。7kN/mBq4m3m4m25、求图示结构C截面转角。已知:q=10kN/m,P=10kN,EI=常数。Pqc4m3m4m26、求图示刚架中铰C两侧截面的相对转角。——23——
《结构力学》习题集(上册)q2EIC2EIlEIEIll27、求图示桁架中D点的水平位移,各杆EA相同。PDaa28、求图示桁架A、B两点间相对线位移∆AB,EA=常数。AaBPPaaab2b29、已知sinucosudu=[sin(u)/2],求圆弧曲梁B点的水平位移,EI=常数。∫aaPBθRπ/2oA30、求图示结构D点的竖向位移,杆AD的截面抗弯刚度为EI,杆BC的截面抗拉(压)刚度为EA。PACD3aB4a2a——24——
《结构力学》习题集(上册)31、求图示结构D点的竖向位移,杆ACD的截面抗弯刚度为EI,杆BC抗拉刚度为EA。BqAaCD2aa232、求图示结构S杆的转角ϕS。(EI=常数,EA=EI/a)。PaSaaa33、刚架支座移动与转动如图,求D点的竖向位移。Da/400a0.01radaa/2a/234、刚架支座移动如图,c1=a/200,c2=a/300,求D点的竖向位移。a/2DaABB"c1A"aac235、图示结构B支座沉陷∆=0.01m,求C点的水平位移。ClAB∆l/2l/2——25——
《结构力学》习题集(上册)36、结构的支座A发生了转角θ和竖向位移∆如图所示,计算D点的竖向位移。AD∆θlll/237、图示刚架A支座下沉0.01l,又顺时针转动0.015rad,求D截面的角位移。DhA0.01l0.015radlllo38、图示桁架各杆温度均匀升高tC,材料线膨胀系数为α,求C点的竖向位移。3/4aCaa39、图示刚架杆件截面为矩形,截面厚度为h,h/l=1/20,材料线膨胀系数为α,求C点的竖向位移。-3t+tC-3t+tlAl40、求图示结构B点的水平位移。已知温变化t1=10℃,t2=20℃,矩形截面高h=0.5m,线膨胀系数a=1/105。t1B6mt1t24m——26——
《结构力学》习题集(上册)41、图示桁架由于制造误差,AE长了1cm,BE短了1cm,求点E的竖向位移。E2cmACB2cm2cm42、求图示结构A点竖向位移(向上为正)∆AV。MEIEIAaEIEI=∞13EIK=a3aa43、求图示结构C点水平位移∆CH,EI=常数。MC6EIBk=l32lAl44、求图示结构D点水平位移∆DH。EI=常数。PDAl3k=3EIlll45、BC为一弹簧,其抗压刚度为k,其它各杆EA=常数,求A点的竖向位移。CDaABPa第四章超静定结构计算——力法——27——
《结构力学》习题集(上册)一、判断题:1、判断下列结构的超静定次数。(1)、(2)、(a)(b)(3)、(4)、(5)、(6)、(7)、(a)(b)2、力法典型方程的实质是超静定结构的平衡条件。3、超静定结构在荷载作用下的反力和内力,只与各杆件刚度的相对数值有关。4、在温度变化、支座移动因素作用下,静定与超静定结构都有内力。5、图a结构,取图b为力法基本结构,则其力法方程为δ11X1=c。cX1(a)(b)6、图a结构,取图b为力法基本结构,h为截面高度,α为线膨胀系数,典型方2程中∆1t=−a(t2−t1)l/(2h)。——28——
《结构力学》习题集(上册)Ath1t2X1l(a)(b)7、图a所示结构,取图b为力法基本体系,其力法方程为。PPkX1(a)(b)二、计算题:8、用力法作图示结构的M图。28kN3CEI3m4kN/mAEIB3m249、用力法作图示排架的M图。已知A=0.2m,I=0.05m,弹性模量为E0。Aq=2kN/mII6m8m10、用力法计算并作图示结构M图。EI=常数。——29——
《结构力学》习题集(上册)Maaaa11、用力法计算并作图示结构的M图。ql/22EIqEIEIll12、用力法计算并作图示结构的M图。q=2kN/mBCEIEI4mA3m4m13、用力法计算图示结构并作出M图。EI=常数。(采用右图基本结构。)PPX1X22l/3l/3l/32l/3l/314、用力法计算图示结构并作M图。EI=常数。q=10kN/m6m3m3m15、用力法计算图示结构并作M图。EI=常数。——30——
《结构力学》习题集(上册)q=16kN/m4m2m2m2m2m16、用力法计算图示结构并作M图。EI=常数。qllll17、用力法计算并作图示结构M图。EI=常数。PPllll18、用力法计算图示结构并作弯矩图。100kN100kNCDEI2EI2EI4mAB1m6m1m19、已知EI=常数,用力法计算并作图示对称结构的M图。qqEA=∞lll20、用力法计算并作图示结构的M图。EI=常数。——31——
《结构力学》习题集(上册)aqqaaa21、用力法作图示结构的M图。EI=常数。qql2l22、用力法作M图。各杆EI相同,杆长均为l。P23、用力法计算图示结构并作M图。EI=常数。4kN.m2kN4m4m4m2m24、用力法计算并作出图示结构的M图。E=常数。P2III6m2III6m8m25、用力法计算图示结构并作M图。EI=常数。——32——
《结构力学》习题集(上册)20kN4m3m4m3m26、用力法计算图示结构并作M图。EI=常数。PPll/2l/2ll/2l/227、利用对称性简化图示结构,建立力法基本结构(画上基本未知量)。E=常数。PIII2IIl2I2II2IIlIIll28、用力法计算图示结构并作M图。E=常数。PPIII2IIlIIPPl/2l/2l/2l/229、已知EA、EI均为常数,用力法计算并作图示结构M图。——33——
《结构力学》习题集(上册)mCDlEFlABll30、求图示结构A、D两固定端的固端力矩,不考虑轴力、剪力的影响。PA2EIBEIl/2DC2EIll31、选取图示结构的较简便的力法基本结构。EI=常数。6m240kN6m6m6m32、选择图示结构在图示荷载作用下,用力法计算时的最简便的基本结构。IPPIA=∞IIIII2I33、用力法求图示桁架杆AC的轴力。各杆EA相同。PADaBCa34、用力法求图示桁架杆BC的轴力,各杆EA相同。——34——
《结构力学》习题集(上册)PCDaABa35、用力法计算图示桁架中杆件1、2、3、4的内力,各杆EA=常数。P2d143ddd36、用力法求图示桁架DB杆的内力。各杆EA相同。PBD4m4m4m4m4m37、用力法作图示结构杆AB的M图。各链杆抗拉刚度EA1相同。梁式杆抗弯刚度2为EI,EI=aEA1100,不计梁式杆轴向变形。BPaCaAa38、用力法计算并作出图示结构的M图。已知EI=常数,EA=常数。PPEIEAEAEA2aaaaa239、用力法计算并作图示结构M图,其中各受弯杆EI=常数,各链杆EA=EI(4l)。——35——
《结构力学》习题集(上册)lPll40、图示结构支座A转动θ,EI=常数,用力法计算并作M图。lAθl41、图a所示结构EI=常数,取图b为力法基本结构列出典型方程并求∆1c和∆2c。ccX1lθX2l(a)(b)42、用力法计算图示超静定梁并作M图。E=常数。ϕ=12IIl/2l/243、用力法计算并作图示结构由支座移动引起的M图。EI=常数。cclll44、用力法计算并作图示结构由支座移动引起的M图。EI=常数。——36——
《结构力学》习题集(上册)ClABcl/2l/245、用力法作图示结构的M图。EI=常数,截面高度h均为1m,t=20℃,+t为温度升高,-t为温度降低,线膨胀系数为α。-t-t+t8m6m46、用力法计算图示结构由于温度改变引起的M图。杆件截面为矩形,高为h,线膨胀系数为α。-10�CEI+10�Cl47、用力法计算并作图示结构的M图,已知:α=0.00001及各杆矩形截面高52h=0.3m,EI=2×10kN⋅m。�+10CEI��+10CEI+30C4m6m——37——
《结构力学》习题集(上册)48、图示连续梁,线膨胀系数为α,矩形截面高度为h,在图示温度变化时,求MB的值。EI为常数。�+20C�-10CB-10�Cll49、已知EI=常数,用力法计算,并求解图示结构由于AB杆的制造误差(短∆)所产生的M图。Aa/2EA=ooa/2Baa50、求图示单跨梁截面C的竖向位移∆CV。ϕ∆EICBAl/2l/251、图示等截面梁AB,当支座A转动θA,求梁的中点挠度fC。θACEIABfCl/2l/252、用力法计算并作图示结构M图。EI=常数,Kϕ=EIl。PKϕl2l2l——38——
《结构力学》习题集(上册)53、图b为图a所示结构的M图,求B点的竖向位移。EI为常数。2qql3AB2lql82ql6(a)(b)M图54、求图示结构中支座E的反力RE,弹性支座A的转动刚度为k。kqBEIAEA=∞CDEEIEIlll55、用力法作图示梁的M图。EI=常数,已知B支座的弹簧刚度为k。1AB3k=EI/ll3EI56、用力法计算图示结构并作M图。EI=常数,k=。35aPkaaa第五章超静定结构计算——位移法一、判断题:1、判断下列结构用位移法计算时基本未知量的数目。(1)(2)(3)——39——
《结构力学》习题集(上册)PCEA=ooDEI1EI=ooGBEEI2EI1EI1AFH(4)(5)(6)EI=EIEIEI=EAb2EI2EI2EIEAEI=a4EI4EI4EI2、位移法求解结构内力时如果MP图为零,则自由项R1P一定为零。3、位移法未知量的数目与结构的超静定次数有关。4、位移法的基本结构可以是静定的,也可以是超静定的。5、位移法典型方程的物理意义反映了原结构的位移协调条件。6、图示结构,当支座B发生沉降∆时,支座B处梁截面的转角大小为1.2∆/l,方向为顺时针方向,设EI=常数。B∆ll7、图示梁之EI=常数,当两端发生图示角位移时引起梁中点C之竖直位移为(3/8)lθ(向下)。2θθCl/2l/28、图示梁之EI=常数,固定端A发生顺时针方向之角位移θ,由此引起铰支端B之转角(以顺时针方向为正)是-θ/2。θBAl39、用位移法可求得图示梁B端的竖向位移为ql/24EI。——40——
《结构力学》习题集(上册)qAELBl二、计算题:10、用位移法计算图示结构并作M图,各杆线刚度均为i,各杆长均为l。qDCBA11、用位移法计算图示结构并作M图,各杆长均为l,线刚度均为i。qCBA12、用位移法计算图示结构并作M图,横梁刚度EA→∞,两柱线刚度i相同。qh2h13、用位移法计算图示结构并作M图。EI=常数。lPPl2EI2EIEIll/2l/2l14、求对应的荷载集度q。图示结构横梁刚度无限大。已知柱顶的水平位移为512/(3EI)(→)。qEIEIEI8m12m12m——41——
《结构力学》习题集(上册)15、用位移法计算图示结构并作M图。EI=常数。lqlll16、用位移法计算图示结构,求出未知量,各杆EI相同。A16kN/m4m20kNBD4mCE4m17、用位移法计算图示结构并作M图,EI=常数。10kN3m3m3m18、用位移法计算图示结构并作M图。3kN2kN/mii2i6m6m2m19、用位移法计算图示结构并作M图。2i2iqiiilll——42——
《结构力学》习题集(上册)20、用位移法计算图示结构并作M图。各杆EI=常数,q=20kN/m。qCDE6mAB6m6m21、用位移法计算图示结构并作M图。EI=常数。l/2P/2l/2l/2P/2l/2l22、用位移法计算图示结构并作M图,E=常数。I2I2m10kNI=1II2m2m23、用位移法计算图示结构并作M图。EI=常数。2qqllll24、用位移法计算图示结构并作M图。EI=常数。——43——
《结构力学》习题集(上册)qII2I2Illl25、用位移法计算图示结构并作M图。l=4m。60kN/mm2EI2EIEIEIlll26、用位移法计算图示结构并作M图。EI1=2EI6mEI1=30kN/m2EI2EIEI6m27、用位移法计算图示刚架并作M图。已知各横梁EI1=∞,各柱EI=常数。PDEhPBChAh28、用位移法计算图示结构并作M图,EI=常数。4kN/m3m5m5m4m29、用位移法计算图示结构并作M图。设各杆的EI相同。——44——
《结构力学》习题集(上册)lqql/2l/230、用位移法作图示结构M图。并求AB杆的轴力,EI=常数。PlAEA=BllPl31、用位移法作图示结构M图。EI=常数。l/2qqlll32、用位移法作图示结构M图。EI=常数。ql/2l/2qll33、用位移法计算图示结构并作出M图。——45——
《结构力学》习题集(上册)30KN/m2EIEIEI4m2EIEIEI4m6m34、用位移法计算图示结构并作M图,E=常数。40kNII2mII4mI3II4m2I2I4m2m2m4m35、用位移法计算图示结构并作M图。EI=常数。qllllll36、用位移法计算图示对称刚架并作M图。各杆EI=常数。CDqlEFlAB2l37、用位移法计算图示结构并作M图。EI=常数。——46——
《结构力学》习题集(上册)PPll/2lll/238、用位移法计算图示结构并作M图。EI=常数。q1.5lllll39、用位移法计算图示结构并作M图。EI=常数。lqll40、用位移法计算图示结构并作M图。设各柱相对线刚度为2,其余各杆为1。60kN3m3m3m41、用位移法计算图示结构并作M图。——47——
《结构力学》习题集(上册)qEI2EIlEIEIq2EIlll42、用位移法计算图示结构并作M图。PEI=13mEIEIEA=3m2m2m43、用位移法计算图示结构并作M图。EI=常数。qlqlqqlll44、用位移法计算图示结构并作M图,C支座下沉∆,杆长为l。2EIBEIC∆45、用位移法计算图示结构并作M图。杆长均为l,支座A下沉c。BAEIc2EI46、用位移法计算图示结构并作M图。——48——
《结构力学》习题集(上册)BEI=∞CliiADαl47、用位移法计算图示结构并作M图。EI=常数。lθll48、已知B点的位移∆,求P。∆ABl/2PEI=l/2ll49、用位移法计算图示结构并作M图。E=常数。θI2Ill50、图示对称刚架制造时AB杆件短了Δ,用位移法作M图。EI=常数。A2lB4l51、用位移法计算图示结构并作M图。——49——
《结构力学》习题集(上册)qEIEI=1ll52、用位移法计算图示刚架,作M图。除注明者外各杆EI=常数。qAFBlCDEI1=ll53、用位移法计算图示刚架,作M图。除注明者外各杆EI=常数。PDEFEI1=ABCll54、用位移法计算图示刚架作M图。除注明者外各杆EI=常数,EI1=∞。qClEI1EI1ADEBll/2l/2l255、图示结构C为弹性支座,弹簧刚度k=i/l,用位移法计算,并作M图。AqBCiikll56、用位移法计算图示结构并作M图。E=常数。——50——
《结构力学》习题集(上册)P/l3k=EI/lI1=Pl/2IIIl/2ll57、用位移法计算图示结构并作M图。EI=常数,k0=EI/l。PEA=lk0l58、用位移法计算图示结构并作M图。PEI=EI13k=EI/l2ll/2l/2EI59、用位移法求图示梁的M图。已知EI=常数,B支座弹簧刚度k=。3l1Bk=EI/l3l360、用位移法作图示结构的M图。弹簧刚度系数k=EI/l,设EI=常数。qkl第六章超静定结构计算——力矩分配法——51——
《结构力学》习题集(上册)一、判断题:1、力矩分配法中的分配系数、传递系数与外来因素(荷载、温度变化等)有关。2、若图示各杆件线刚度i相同,则各杆A端的转动刚度S分别为:4i,3i,i。AAA3、图示结构EI=常数,用力矩分配法计算时分配系数µ=4/11。A42l1A3l4ll4、图示结构用力矩分配法计算时分配系数µAB=1/2,µAD=1/8。Ci=1BADi=1i=1i=1E5、用力矩分配法计算图示结构,各杆l相同,EI=常数。其分配系数µBA=0.8,µBC=0.2,µBD=0。ACBD6、在力矩分配法中反复进行力矩分配及传递,结点不平衡力矩愈来愈小,主要是因为分配系数及传递系数<1。37、若用力矩分配法计算图示刚架,则结点A的不平衡力矩为−M−Pl。16——52——
《结构力学》习题集(上册)DIlMPC3IBA2I1.5IlEll/2l/2二、计算题:8、用力矩分配法作图示结构的M图。已知:M0=15kN⋅m,µBA=3/7,µBC=4/7,P=24kN。M0PABC3m3m9、用力矩分配法计算连续梁并求支座B的反力。.m20kN50kN10kN/mDA2EIBEIC6m4m2m10、用力矩分配法计算图示结构并作M图。EI=常数。PClIBADI2Ill11、用力矩分配法作图示梁的弯矩图。EI为常数。(计算两轮)10kN5kN2kN/mABCDE2m2m8m6m2m——53——
《结构力学》习题集(上册)12、用力矩分配法作图示梁的弯矩图。EI为常数。(计算两轮)10kN6kN/mABCDE8m8m6m3m13、计算图示结构的力矩分配系数和固端弯矩。16kN20kN/mABCDi=1i=2i=14m10m1m14、用力矩分配法作图示连续粱的M图。(计算两轮)3kN/m24kNi=4i=3i=26m8m3m3m15、用力矩分配作图示连续粱的M图。(计算两轮)56kN6kN/mEI2EIEI3m3m8m6m16、用力矩分配法作图示结构M图。Pm/lmBDAEICEIl2ll17、求图示结构的力矩分配系数和固端弯矩。EI=常数。100kN30kN/mBAD30kN.m4mC4m2m2m——54——
《结构力学》习题集(上册)18、已知:q=20kN/m,µ=0.32,µ=0.28,µ=0.25,µ=0.15。用ABACADAE力矩分配法作图示结构的M图。DqECAB4m19、已知:q=20kN/m,M0=100kN⋅m,µAB=0.4,µAC=0.35,µAD=0.25。用力矩分配法作图示结构的M图。qM0BADC6m20、已知图示结构的力矩分配系数µA1=8/13,µA2=2/13,µA3=3/13,作M图。160.m10kN/mkN021A2m40kN2m34m4m21、求图示结构的力矩分配系数和固端弯矩。B12kN/m32kNADEI1.5EI2EI4mC3m2.5m2.5m22、求图示结构的力矩分配系数和固端弯矩。EI=常数。——55——
《结构力学》习题集(上册)100kN30kN/mBAD30kN.m4mC4m2m2m23、用力矩分配法作图示结构M图。已知:P=10kN,q=2.5kN/m,各杆EI相同,杆长均为4m。qPBDAC24、用力矩分配法作图示结构的M图。已知:P=10kN,q=2kN/m,横梁抗弯刚度为2EI,柱抗弯刚度为EI。qPDCB6mA3m3m3m25、用力矩分配法计算图示结构,并作M图。qEI2EIl3EIll26、用力矩分配法计算并作图示结构M图。EI=常数。——56——
《结构力学》习题集(上册)8kNBA2IID6mIC3m3m3m27、求图示结构的力矩分配系数和固端弯矩。已知q=20kN/m,各杆EI相同。qDAC1.5m3mB2m2m28、用力矩分配法计算图示结构,并作M图。(EI=常数)M2MMlllll29、用力矩分配法作图示对称刚架的M图。EI为常数。EA=∞。(计算二轮)P=10kN2mEA2m2m2m30、用力矩分配法作图示对称刚架的M图。EI=常数。——57——
《结构力学》习题集(上册)80kNmABE36kNm36kNm2mFCD80kNm3m3m31、用力矩分配法计算图示对称结构,并作M图。EI=常数。P=10kNP=10kNq=20kN/m5m2m5m5m2m32、用力矩分配法计算图示结构并作M图。各杆线刚度比值如图所示。20kN/m242116m6m9m6m33、用力矩分配法作图示结构的M图。各杆的线刚度比值如图所示。8kN3116m33m3m34、用力矩分配法计算图示对称结构并作出M图。EI=常数。——58——
《结构力学》习题集(上册)20kN4m4m2m2m4m35、用力矩分配法作图示对称结构的M图。(EI=常数)qIII2II6m4m4m36、图a所示结构的力矩分配系数与固端弯矩如图b所示,作结构M图。(计算二轮)4i,l/2BABEBC(a)ABC(b)1/32/38/153/154/152i,l2-12-12000lilii∆()lDE40θ=∆l∆37、用力矩分配法计算图示结构并作M图。2EIEIEIl∆ll38、已知图示结构支座下沉∆B=0.01m,∆C=0.015m,各杆EI=4.2×104kN·m2,用力矩分配法作M图。(计算二轮)——59——
《结构力学》习题集(上册)ABCD6m6m6m39、已知:各杆EI=6×104kN·m2,用力矩分配法作图示结构由于荷载及支座移动引起的M图。(计算二轮)。40kN/m0.01m0.01m3m4m6m2m40、用力矩分配法计算图示结构并作M图。MEIk=4ϕlEIEIll第七章影响线及其应用一、判断题:1、图示结构MC影响线已作出如图(a)所示,其中竖标yE表示P=1在E时,C截面的弯矩值。P=160kN60kNAECDB2mABCMC6my12mE(a)(b)2、图(b)所示梁在给定移动荷载作用下,支座B反力最大值为110kN。二、作图、计算题:3、作图示梁中RA、ME的影响线。——60——
《结构力学》习题集(上册)AEBCDaaa2a4、单位荷载在梁DE上移动,作梁AB中RB、MC的影响线。P=1DEABCaa2a5、作图示结构RB、QB右影响线。P=1ABCDE4m2m2m4m6、作图示梁的MK、QE影响线。KEF2aaaaaaaa7、单位荷载在刚架的横梁上移动,作MA的影响线(右侧受拉为正)。xP=1lAl2l8、图示结构P=1在DG上移动,作MC和QC右的影响线。P=1DEFGACB4m4m4m4m9、作图示结构的MB影响线。——61——
《结构力学》习题集(上册)P=1ABDE4m4m4m2m10、作图示结构:(1)当P=1在AB上移动时,MA影响线;(2)当P=1在BD上移动时,MA影响线。P=1BCDP=1lAll11、作图示结构的MC、QF影响线。设MC以左侧受拉为正。P=1ABCDFl/2l/2l/2l/212、单位荷载在桁架上弦移动,求Na的影响线。xP=1ACDBadddd13、单位荷载在桁架上弦移动,求Na的影响线。xP=1AaCdBddd——62——
《结构力学》习题集(上册)14、作图示桁架的V3影响线。P=1V3aaaaa15、单位荷载在DE上移动,求主梁RA、MC、QC的影响线。P=1DEACB2m2m11112mQ16、作图示结构C右的影响线。P=1EFGHDABClllllll17、作出图示梁MA的影响线,并利用影响线求出给定荷载下的MA值。20kN5kN/mA2m2m1m18、P=1沿AB及CD移动。作图示结构MA的影响线,并利用影响线求给定荷载作用下MA的值。40kN/mCD100kN2mAB2m2m4m19、作图示梁的QC的影响线,并利用影响线求给定荷载作用下QC的值。——63——
《结构力学》习题集(上册)30kN/m100kN20kN/mABCDEF3m1m3m3m2m2m20、图示静定梁上有移动荷载组作用,荷载次序不变,利用影响线求出支座反力RB的最大值。2m48kN40kNABC6m4m21、绘出图示结构支座反力RB的影响线,并求图示移动荷载作用下的最大值。(要考虑荷载掉头)1kN3kN3kNP=1BDC1m2mE4mA4m2m4m第八章矩阵位移法一、判断题:1、单元刚度矩阵反映了该单元杆端位移与杆端力之间的关系。2、单元刚度矩阵均具有对称性和奇异性。3、局部坐标系与整体坐标系之间的坐标变换矩阵T是正交矩阵。4、结构刚度矩阵反映了结构结点位移与荷载之间的关系。5、结构刚度方程矩阵形式为:[K]{∆}={P},它是整个结构所应满足的变形条件。6、图示结构用矩阵位移法计算时(计轴向变形)未知量数目为8个。——64——
《结构力学》习题集(上册)7、在直接刚度法的先处理法中,定位向量的物理意义是变形连续条件和位移边界条件。8、等效结点荷载数值等于汇交于该结点所有固端力的代数和。9、矩阵位移法中,等效结点荷载的“等效原则”是指与非结点荷载的结点位移相等。10、矩阵位移法既能计算超静定结构,也能计算静定结构。11、已知图示刚架各杆EI=常数,当只考虑弯曲变形,且各杆单元类型相同时,采用先处理法进行结点位移编号,其正确编号是:B.A.2(0,1,2)2(1,2,0)4(0,0,0)4(0,0,0)1(0,0,0)1(0,0,0)3(0,1,3)3(0,0,3)C.D.yM,θ2(1,0,2)2(0,1,2)x1(0,0,0)4(0,0,0)1(0,0,0)4(0,0,0)(1,0,3)3(0,3,4)()3二、计算题:12、用先处理法计算图示结构刚度矩阵的元素K,K,K。2233131(0,0,0)2(0,0,1)3(0,2,3)4(0,0,0)EI2EI(0,2,4)EIylEAM,θx5(0,0,0)lll——65——
《结构力学》习题集(上册)13、用先处理法计算图示刚架结构刚度矩阵的元素K,K,K。EI,EA均为常223415数。2(2,3,4)3(0,5,0)lyM,θ1(0,0,1)xl14、计算图示结构整体刚度矩阵的元素K,K,K。E为常数。4455661A,I22A,2I3A2AAl/2yM,θ4xll15、写出图示结构以子矩阵形式表达的结构原始刚度矩阵的子矩阵[K22],[K24]。21:3ii[k11][k12]yiM,θ[k]=iix4[k21][k22]16、已知平面桁架单元在整体坐标系中的单元刚度矩阵,计算图示桁架结构原始刚度矩阵[K]中的元素K,K,EA=常数。C=cosα,S=sinα,A=C⋅C,7778B=C⋅S,D=S⋅S,各杆EA相同。34iA−B−ABiEADB−Dl[k]=lA−BiD12yyxlαx——66——
《结构力学》习题集(上册)17、计算图示刚架结构刚度矩阵中的元素K,K(只考虑弯曲变形)。设各层高1188度为h,各跨长度为l,h=0.5l,各杆EI为常数。d1d1d1d2d3d4d5d5d5yM,θd6d7d8x18、计算图示结构原始刚度矩阵的元素K,K。4445②23A①③lII14l19、用先处理法写出图示梁的整体刚度矩阵[K]。0123yi1i2i3M,θxlll20、用先处理法写出图示梁的结构刚度矩阵[K]。1234y2EIEI3EIM,θlllx21、已知图示结构在整体坐标系中的单元刚度矩阵。用先处理法集成结构刚度矩阵[K]。(用子块形式写出)。——67——
《结构力学》习题集(上册)5:3ii4[k11][k12]i[k]=ii[k21][k22]1222、用先处理法写出图示结构的结构刚度矩阵[K]。E=常数。P1(0,0,0)M3(0,0,3)y2I2(0,1,2)IM,θxll23、用先处理法写出图示刚架的结构刚度矩阵[K],只考虑弯曲变形。EI=ooEIEIEIlyM,θxll24、用先处理法写出图示结构的结构刚度矩阵[K]。各杆长度为l,EA、EI为常数。CyM,θxDAB25、用先处理法写出图示结构的结构刚度矩阵[K]。各杆长度为l。CEAyM,θDx2EIEIAB——68——
《结构力学》习题集(上册)26、用先处理法写出以子块表示的图示结构的结构刚度矩阵[K]。23②①③6m1412m27、用先处理法写出图示桁架的结构刚度矩阵[K]。已知各杆EA=常数。⎡10−10⎤⎢⎥①②EA⎢0000⎥[k]=[k]=l⎢−1010⎥⎢⎥⎣0000⎦,整体坐标系中的单元刚度矩阵:1③⎡1−1−11⎤l①⎢⎥y③2EA⎢−111−1⎥[k]=2②x4l⎢−111−1⎥3⎢⎥⎣1−1−11⎦l28、用先处理法写出图示刚架结构刚度矩阵[K]。已知:⎡30000−30000⎤⎢⎥012300−1230⎢⎥①②③⎢0301000−3050⎥4[k]=[k]=[k]=10×⎢⎥⎢−3000030000⎥⎢0−12−30012−30⎥⎢⎥⎢⎣030500−30100⎥⎦——69——
《结构力学》习题集(上册)123①②③yM,θx429、计算图示结构结点3的等效结点荷载列阵{P3E}。3kN/m2352m4kN4kNy2mM,θ146x4m4m30、计算图示结构结点2的等效结点荷载列阵{P2E}。ql23lqqyM,θ14xl/2l/231、计算图示结构结点2的等效结点荷载列阵{P2E}。qlq1234yM,θxl/2l/2ll32、计算图示结构的综合结点荷载列阵{P}。——70——
《结构力学》习题集(上册)ql2qqlqql4(0,0,4)y0(0,0,0)1(0,0,1)2(0,0,2)3(0,0,3)M,θxll/2l/2ll/2l/233、计算图示连续梁对应于自由结点位移的荷载列阵{P}。PPq1M23yM,θxl/2l/2l34、计算图示连续梁对应于自由结点位移的荷载列阵{P}。20kN10kN6kN/my1234M,θx3m3m4m4m35、用先处理法计算图示连续梁的结点荷载列阵{P}。2kN4kN5kNm.12kN/myM,θ2EIEIEIx4m4m4m36、计算图示结构的综合结点荷载列阵元素P,P,P。134q4(0,5,6)l2ql2(1,2,3)l/2ql3(0,0,4)yM,θl/2x1(0,0,0)l——71——
《结构力学》习题集(上册)37、用先处理法计算图示结构的综合结点荷载列阵{P}。q2ql23l/2qlyM,θl/2x1l38、计算图示结构结点荷载列阵中的元素P,P,P。4565(0,7,8)qqll3(1,2,3)4(4,5,6)lyqM,θx1(0,0,0)2(0,0,0)l/2l/239、计算图示结构综合结点荷载列阵中的元素P,P,P。134P3MqP2(2,3,4)l/2(0,0,0)P1yl/2M,θ(0,0,1)xl40、计算图示结构综合结点荷载列阵{P}中的元素P,P,P,P。3789——72——
《结构力学》习题集(上册)ql25lql2qlq132yqlM,θx4ll41、计算图示刚架对应于自由结点位移的综合结点荷载列阵{P}。10kN24kN5kN23y3kN/m4mM,θ14x3m3m42、计算图示刚架对应自由结点位移的综合结点荷载列阵{P}。各杆长度为4m。10kN3kN/m10kNq235y3kN/mM,θx1443、计算图示结构结点2的综合结点荷载列阵{P2}。PPPPl/2123lPyl/2M,θ4xl/2l/2l44、计算图示刚架考虑弯曲、轴向变形时的综合结点荷载列阵{P}。——73——
《结构力学》习题集(上册)1EI,EA7kNm.10kNm.2EA=oo2kNEI=oo35kNyM,θ8kNEI,EAx445、若考虑弯曲、轴向变形,用先处理法写出图示结构综合结点荷载列阵{P}。2ql2qql123l/2qlyM,θl/24xll46、考虑弯曲、轴向变形,计算图示结构综合结点荷载列阵{P}。20kN10kNm.40kN12kN/m234myM,θx13m2m2m47、考虑弯曲、轴向变形时,用先处理法计算图示结构综合结点荷载列阵{P}。5kNm.2kN4.8kN/m6kN122.5m8kNy2.5mM,θ3x5m48、用先处理法计算图示结构的综合结点荷载列阵{P}。——74——
《结构力学》习题集(上册)4l/2Pqyl/2M,θ312xll49、用先处理法计算图示桁架的综合结点荷载列阵{P}。10kN3myM,θx4m50、计算图示结构的自由结点荷载列阵{P}。20kN3110kN6myM,θ4230kNx40kN8m51、计算图示结构中杆12的杆端力列阵中的第6个元素。已知杆12的杆端位移列T阵为{δ12}=[00−0.3257−0.0305−0.1616−0.1667]。1kN/m132y0.5mM,θx4EA=1kN1m1mEI=1kNm.252、计算杆14的轴力。已知图示桁架EA=1kN,结点位移列阵为:T{∆}=[002.56770.04151.04151.36731.6092−1.72651.640801.2084−0.4007]。——75——
《结构力学》习题集(上册)1kN1kN2461my15M,θ3x1m1m53、计算杆23的杆端力列阵的第2个元素。已知图示结构结点位移列阵为:T{∆}=[000-0.1569-0.23380.4232000]。1kNm.1kN/m230.5mEA=1kN1kNEI=1kNm.yM,θ0.5mx11m54、计算图示结构中杆34的杆端力列阵中的第3个元素和第6个元素。不计杆件的轴向变形。已知图示结构结点位移列阵为:T{∆}=[000−0.200.1333−0.20.20.333300.36670−0.75560.20.6667]。1kN25A(m)4I(m)A=I=1.51m234A=I=1A=I=11mA=I=2yM,θ1E=1kN/m2x(0,0,0)1m1m55、已知图示桁架的结点位移列阵(分别为结点2、4沿x、y方向位移)为:T{∆}=(1/(EA))×[342.322−1139.555−137.680−1167.111],设各杆EA为常数。计算单元①的内力。——76——
《结构力学》习题集(上册)40kN1220kN3myM,θ360kNx440kN4m56、已知图示桁架杆件①的单元刚度矩阵为式(a),又已知各结点位移为式(b),则①杆件①的轴力(注明拉力或压力)应为N=。⎧u1⎫⎧5⎫⎪⎪⎪⎪v−1⎪1⎪⎪⎪⎪u⎪⎪0⎪2⎡10−10⎤⎪⎪⎪⎪13v0⎢0000⎥⎪2⎪⎪⎪[]①=EA⎢⎥�(a)⎪�⎪=Pl⎪�⎪�(b)k⎨⎬⎨⎬lyl⎢−1010⎥⎪⎪EA⎪⎪⎢⎥u32M,θ⎣0000⎦⎪⎪⎪⎪2x⎪v3⎪⎪3⎪4⎪u⎪⎪0⎪⎪4⎪⎪⎪l⎪v⎪⎪0⎪⎩4⎭⎩⎭57、已求得图示结构结点2、3的结点位移为式(a)、(b)并已知单元②的整体坐标的单元刚度矩阵为式(c)。计算单元②2端的弯矩。(长度单位m,力单位kN,角度单位弧度)⎧u2⎫⎧0.2⎫⎧u3⎫⎧−0.3⎫⎪⎪⎪⎪-5⎪⎪⎪⎪-5⎨v2⎬=⎨-160⎬×10��(a),⎨v3⎬=⎨−159.8⎬×10��(b)⎪φ⎪⎪-40⎪⎪φ⎪⎪−10⎪⎩2⎭⎩⎭⎩3⎭⎩⎭⎡1.501.5−1.50−1.5⎤1⎢05000−500⎥2⎢⎥②⎢−1.5021.501⎥5[k]=⎢⎥×10��(c)⎢−1.501.51.501.5⎥y⎢0−5000500⎥M,θ⎢⎥43x⎢⎣−1.5011.502⎥⎦58、计算单元①的轴力。已知图示结构结点1、3的结点位移为:TT[u1v1u3v3]=[5−123]⋅Pl/EA。——77——
《结构力学》习题集(上册)1①3⑤yl②④M,θx2③4l42−22T59、已知各杆的E=2.1×10kN/m,A=10m,{∆}=[0.09524−0.25689]。计2×1算图示桁架单元①的杆端力列阵。2(0,0)3(1,2)2kN3kN4myM,θ1(0,0)x4m③60、计算图示结构单元③的杆端力列阵{F},已知各杆4242E=2.1×10kN/cm,I=300cm,A=20cm,l=100cm,结点2位移列阵{}[]T−2[]T∆=uvθ=1×10×0.4730cm−0.4596cm−0.5313rad。2222yM,θx20kN40kNm.20kN31①2②③l4ll①61、考虑杆件的轴向变形,计算图示结构中单元①的杆端力{F}。已知:4722I=(1/24)m,E=3×10kN/m,A=0.5m。结点1的位移列阵−6T{δ1}=1×10×[3.7002m−2.7101m−5.1485rad]。——78——
《结构力学》习题集(上册)50kNm.2kN4.8kN/m6kN1①22.5m②8kNy2.5mM,θ3x5m①62、计算图示刚架单元①在局部坐标下的杆端力{F}。已知各杆E、A、I、l均为2qlT常数,{∆}=[0027l−527l−1900],不考虑杆件的轴向变形。1000EI2②3yq①③lM,θx14lT2263、已知图示梁结点转角列阵为{∆}=[0-ql/56i5ql/168i],EI=常数。计算B支座的反力。q123yABCM,θx1m1m第九章结构的动力计算一、判断题:1、结构计算中,大小、方向随时间变化的荷载必须按动荷载考虑。2、仅在恢复力作用下的振动称为自由振动。3、单自由度体系其它参数不变,只有刚度EI增大到原来的2倍,则周期比原来的周期减小1/2。4、结构在动力荷载作用下,其动内力与动位移仅与动力荷载的变化规律有关。5、图示刚架不计分布质量和直杆轴向变形,图a刚架的振动自由度为2,图b刚架的振动自由度也为2。——79——
《结构力学》习题集(上册)(a)(b)6、图示组合结构,不计杆件的质量,其动力自由度为5个。7、忽略直杆的轴向变形,图示结构的动力自由度为4个。8、由于阻尼的存在,任何振动都不会长期继续下去。9、设ω,ωD分别为同一体系在不考虑阻尼和考虑阻尼时的自振频率,ω与ωD的关系为ω=ωD。二、计算题:10、图示梁自重不计,求自振频率ω。EIWll/411、图示梁自重不计,杆件无弯曲变形,弹性支座刚度为k,求自振频率ω。WEIookl/2l/2——80——
《结构力学》习题集(上册)12、求图示体系的自振频率ω。mEI2EI0.5l0.5ll13、求图示体系的自振频率ω。EI=常数。ml0.5l14、求图示结构的自振频率ω。mlEI=lll15、求图示体系的自振频率ω。EI=常数,杆长均为l。m16、求图示体系的自振频率ω。杆长均为l。——81——
《结构力学》习题集(上册)EIEA=ooEIEIm17、求图示结构的自振频率和振型。ml/2EImEIEIl/2l/24218、图示梁自重不计,W=200kN,EI=2×10kN⋅m,求自振圆频率ω。WEICBA2m2m19、图示排架重量W集中于横梁上,横梁EA=∞,求自振周期ω。WhEIEI20、图示刚架横梁EI=∞且重量W集中于横梁上。求自振周期T。WEIhEI2EI21、求图示体系的自振频率ω。各杆EI=常数。——82——
《结构力学》习题集(上册)m2aaa22、图示两种支承情况的梁,不计梁的自重。求图a与图b的自振频率之比。EImEIEImEIl/2l/2l/2l/2(a)(b)23、图示桁架在结点C中有集中重量W,各杆EA相同,杆重不计。求水平自振周期T。WC4m3m3m24、忽略质点m的水平位移,求图示桁架竖向振动时的自振频率ω。各杆EA=常数。m3m4m4m42−1425、图示体系E=2×10kN/cm,θ=20s,P=5kN,W=20kN,I=4800cm。求质点处最大动位移和最大动弯矩。PsinθtEIW4m2m——83——
《结构力学》习题集(上册)52-15326、图示体系EI=2×10kN⋅m,θ=20s,k=3×10N/m,P=5×10N。W=10kN。求质点处最大动位移和最大动弯矩。PsinθtkW2m2m27、求图示体系在初位移等于l/1000,初速度等于零时的解答。θ=0.20ω(ω为自振频率),不计阻尼。PsinθtmEI=1oolEIEIl28、图示体系受动力荷载作用,不考虑阻尼,杆重不计,求发生共振时干扰力的频率θ。Psin()θtmEI1=ool/3EIl29、已知:m=3t,P=8kN,干扰力转速为150r/min,不计杆件的质量,32EI=6×10kN⋅m。求质点的最大动力位移。PsinθtmEIEI2m2m——84——
《结构力学》习题集(上册)30、图示体系中,电机重W=10kN置于刚性横梁上,电机转速n=500r/min,水4平方向干扰力为P(t)=2kN⋅sin(θt),已知柱顶侧移刚度k=1.02×10kN/m,自振−1频率ω=100s。求稳态振动的振幅及最大动力弯矩图。P()tW4m31、图示体系中,W=10kN,质点所在点竖向柔度δ=1.917,马达动荷载P(t)=4kNsin(θt),马达转速n=600r/min。求质点振幅与最大位移。P(t)W−132、图示体系中,W=8kN,自振频率ω=100s,电机荷载P(t)=5kN·sin(θt),电机转速n=550r/min。求梁的最大与最小弯矩图。P(t)W2m2m33、求图示体系支座弯矩MA的最大值。荷载P(t)=P0sinθt,θ=0.4ω。ml/2P(t)l/2A34、求图示体系的运动方程。——85——
《结构力学》习题集(上册)Psin(θt)mEI0.5l0.5l35、求图示体系稳态阶段动力弯矩幅值图。θ=0.5ω(ω为自振频率),EI=常数,不计阻尼。Psin()θtmlll36、图示体系分布质量不计,EI=常数。求自振频率。2mm12aa37、图示简支梁EI=常数,梁重不计,m1=2m,m2=m,已求出柔度系数3δ12=7a/(18EI)。求自振频率及主振型。m1m212aaa38、求图示梁的自振频率及主振型,并画主振型图。杆件分布质量不计。mEI=m12aaa39、图示刚架杆自重不计,各杆EI=常数。求自振频率。——86——
《结构力学》习题集(上册)m22mm12m2m40、求图示体系的自振频率和主振型。EI=常数。mml/3l/3l/341、求图示体系的自振频率及主振型。EI=常数。mml/2l/2l/2l/242、求图示体系的自振频率及相应主振型。EI=常数。mm2ll/2l/2l/2l/243、求图示结构的自振频率和主振型。不计自重。mEI=ll/2l/2——87——
《结构力学》习题集(上册)44、求图示体系的自振频率和主振型。不计自重,EI=常数。mm12aaa45、求图示体系的第一自振频率。mEI=ml/2l/2l/2l/246、求图示体系的自振频率。已知:m1=m2=m。EI=常数。m1m21.5m1.5m1m1m1m47、求图示体系的自振频率和主振型,并作出主振型图。已知:m1=m2=m,EI=常数。m1m24m4m2m48、求图示对称体系的自振频率。EI=常数。mml/2l/2l/2l/249、图示对称刚架质量集中于刚性横粱上,已知:m1=m,m2=2m。各横梁的层间侧移刚度均为k。求自振频率及主振型。m22m11——88——
《结构力学》习题集(上册)50、求图示体系的自振频率并画出主振型图。mEI=oo1EIEI6mmEI=oo1EIEI6m51、求图示体系的自振频率和主振型。EI=常数。m2EI=oo0lEImEI1EI0=oolEIEIll52、用最简单方法求图示结构的自振频率和主振型。mlmEI=lll53、求图示体系的频率方程。mmEI=ll54、求图示体系的自振频率和主振型。EI=常数。——89——
《结构力学》习题集(上册)m2aaa55、求图示体系的自振频率和主振型。不计自重,EI=常数。mm12a/2a/2a/2a/256、求图示体系的自振频率。设EI=常数。mll57、图示体系,设质量分别集中于各层横梁上,数值均为m。求第一与第二自振频率之比ω1:ω2。mEI0ooEIEIlmEI0oo2EI2EIl58、求图示体系的自振频率和主振型。mEI=∞EI1EI1l2mEI=∞2EI12EI1ll——90——
《结构力学》习题集(上册)59、求图示体系的自振频率和主振型。m1=m,m2=2m。m1EIlm22EI2EIl60、求图示桁架的自振频率。杆件自重不计。WEAEA4m3m3m61、求图示桁架的自振频率。不计杆件自重,EA=常数。m4m3m3mEI62、作出图示体系的动力弯矩图,已知:θ=0.82567。3mlPsin(θt)EImEIm120.5l0.5l63、作图示体系的动力弯矩图。柱高均为h,柱刚度EI=常数。——91——
《结构力学》习题集(上册)m2EI0=∞EIθ=1.32573mhPsinθt2m1EI0=∞0.5l0.5l−164、绘出图示体系的最大动力弯矩图。已知:动荷载幅值P=10kN,θ=20.944s,62质量m=500kg,a=2m,EI=4.8×10N⋅m。Psin(θt)mPsin(θt)ma4a65、已知图示体系的第一振型如下,求体系的第一频率。EI=常数。3m/2l2m⎧0.1618⎫l⎪⎪1m振型1⎨0.5401⎬l⎪⎪⎩1⎭第十章结构弹性稳定计算一、判断题:1、稳定方程即是根据稳定平衡状态建立的平衡方程。2、压弯杆件和承受非结点荷载作用的刚架丧失稳定都属于第一类失稳。3、在稳定分析中,有n个稳定自由度的结构具有n个临界荷载。4、两类稳定问题的主要区别是:荷载—位移曲线上是否出现分支点。5、静力法确定临界荷载的依据是结构失稳时的静力平衡条件。6、能量法确定临界荷载的依据是势能驻值原理。——92——
《结构力学》习题集(上册)二、计算题:7、用静力法推导求临界荷载P的稳定方程。crPEI,l8、写出图示体系失稳时的特征方程。ABPEIkkϕl9、求刚架在反对称失稳时的稳定方程。n为常数。PPBDEIEIlnEIACl210、求图示完善体系的临界荷载Pcr。转动刚度kr=kl,k为弹簧刚度。EIOOEIOOPkkkrll311、求图示刚架的临界荷载P。已知弹簧刚度k=3EIl。cr——93——
《结构力学》习题集(上册)PBEI0OOlAEICkl12、求图示中心受压杆的临界荷载P。crPEIl13、用静力法求图示结构的临界荷载P,欲使B铰不发生水平移动,求弹性支承cr的最小刚度k值。PBkEIlA14、用静力法确定图示具有下端固定铰,上端滑动支承压杆的临界荷载P。crPδPlEIyxy——94——
《结构力学》习题集(上册)15、用能量法求图示结构的临界荷载参数P。设失稳时两柱的变形曲线均为余弦crbbπx2⎡u1⎤曲线:y=δ(1−cos).提示:∫cosudu=⎢+sin2u⎥。2ha⎣24⎦aP2PEAEI3EIh16、用能量法求中心受压杆的临界荷载P与计算长度,BC段为刚性杆,AB段失稳cr3x时变形曲线设为:y(x)=a(x−).2lxPCEI→∞0lBEIlAy17、用能量法求图示体系的临界荷载P。crPEI1=HEIl——95——
《结构力学》习题集(上册)18、用能量法求图示中心压杆的临界荷载P,设变形曲线为正弦曲线。提示:crbb2⎡u1⎤∫Sinudu=⎢−Sin2u⎥a⎣24⎦aPl2EIl22219、设y=Ax(l−x),用能量法求临界荷载P。crPyEI,lx第十一章结构的极限荷载一、判断题:1、静定结构只要产生一个塑性铰即发生塑性破坏,n次超静定结构一定要产生n+1个塑性铰才产生塑性破坏。2、塑性铰与普通铰不同,它是一种单向铰,只能沿弯矩增大的方向发生相对转动。3、超静定结构的极限荷载不受温度变化、支座移动等因素影响。4、结构极限荷载是结构形成最容易产生的破坏机构时的荷载。5、极限荷载应满足机构、内力局限和平衡条件。6、塑性截面系数W和弹性截面系数W的关系为W=W。ss二、计算题:7、设M为常数。求图示梁的极限荷载M及相应的破坏机构。uu——96——
《结构力学》习题集(上册)ABMl8、设极限弯矩为M,用静力法求图示梁的极限荷载。uPMuACBl/32l/39、图示梁各截面极限弯矩均为M,欲使A、B、D三处同时出现塑性铰。确定铰uC的位置,并求此时的极限荷载P。uxPCDABabl10、画出下列变截面梁极限状态的破坏机构图。P()a3MuMu0.4l0.3l0.3lP()b3MuMu0.3l0.35l0.35lP()c3MuMul/3l/3l/311、图示简支梁,截面为宽b高h的矩形,材料屈服极限σ。确定梁的极限荷载P。yuPPl/3l/3l/3——97——
《结构力学》习题集(上册)12、图示等截面梁,截面的极限弯矩为M=90kN⋅m,确定该梁的极限荷载P。uuPPMu2m2m2m13、图示等截面梁,截面的极限弯矩M=90kN⋅m,求极限荷载P。uuP2m4m14、求图示梁的极限荷载P。已知极限弯矩为M。uuqABl15、图示梁截面极限弯矩为M。求梁的极限荷载P,并画出相应的破坏机构与uuM图。P0.4PBCDAEF0.5l0.5l0.5l0.5l0.5l16、求图示梁的极限荷载q。u2qaqAMuBMuCa2aa2a——98——
《结构力学》习题集(上册)17、求图示结构的极限荷载P。AC段及CE段的M值如图所示。uu10P5P6PBMu=80kNmAMu=100kNmCDE2m2m2m2m18、求图示结构的极限荷载P,并画极限弯矩图。各截面M相同。uuPq=4/3PABCFDEMu=20kN.mP2m1m3m1.5m1.5m19、求图示结构的极限荷载P,并画极限弯矩图。M=常数。uuPPABCD2P2llll2ll20、计算图示等截面连续梁的极限荷载P。uA2PPDBECMuMu2l/3l/3l/2l/221、求图示等截面连续梁的屈服荷载P和极限荷载P。yuPABCDMuMul/2l/2l/222、求图示梁的极限荷载q。u——99——
《结构力学》习题集(上册)qMu1.5MuMul3l3lll23、计算图示梁的极限荷载P。uPq=P/l3Mu1.5Mul/32/3ll24、计算图示结构在给定荷载作用下达到极限状态时,其所需的截面极限弯矩值M。uq3q2MuMu6m2m2m25、求图示梁的极限荷载P。uMuPl/2l/226、求图示连续梁的极限荷载q。uqMu2Mul2l27、求图示连续梁的极限荷载P。u——100——
《结构力学》习题集(上册)P/l2PPMuMuMul/2l/2ll/2l/228、计算图示结构的极限荷载q。已知:l=4m。u2qqqA4BCDMuMu1.2Mu2l/3l/3l/2l/2l29、计算图示结构在给定荷载作用下达到极限状态时,其所需截面极限弯矩值M。u20kN10kN/m40kNMuMu1.2Mu4m2m2m2m2m30、图示等截面梁,其截面承受的极限弯矩M=6540kN⋅cm,有一位置可变的u荷载P作用于梁上,移动范围在AD内,确定极限荷载P值及其作用位置。uPADBC62m4mm31、图示等截面梁,截面的极限弯矩M=80kN⋅m,求极限荷载q。uuq4m2m——101——
《结构力学》习题集(上册)32、图示等截面的两跨连续梁,各截面极限弯矩均为M,确定该梁的极限荷载quu及破坏机构。qCABqll33、求图示梁的极限荷载q。截面极限弯矩M=140.25kN⋅m。uuqlqP=2ABCD8m4m4m8m34、求图示连续梁的极限荷载P。uPq=P/()2aP2PABMC4MDMuuua/2a/22aaaa35、求图示结构的极限荷载P。uP3MuMu2Mu4m2m2m36、求图示结构的极限荷载P。uPADCBM=4kN.mM=2.4kN.muu2m1m2m——102——
《结构力学》习题集(上册)37、求图示梁的极限荷载P。uPP2MuMu2Mul/4l/2l/438、画出图示变截面梁的破坏机构并确定极限荷载P。uPABC3MuMu3a3a3a39、求图示刚架的极限荷载参数q并画M图。M为极限弯矩。uuP=ql2MuMulql/2l/240、图示刚架各截面极限弯矩均为M,欲使B,C,D,E截面同时出现塑性铰而u成机构。求P与q的关系并求极限荷载P,Q。uuqPDBClEAl/2l/2——103——
《结构力学》习题集(上册)41、讨论图示变截面梁的极限荷载P。已知AB段截面的极限弯矩为M′,BC段uu截面的极限弯矩为M,且M′>M。uuuPABDCM"Muuaaa答案第一章平面体系的几何组成分析(参考答案)1、(O)2、(X)3、7、9、10、11、13、14、17、18、19、20、22、23、25、27、28、30、31、32、33、均是无多余约束的几何不变体系。4、8、12、29、均是几何瞬变体系。5、15、均是几何可变体系。6、21、24、26、均是有一个多余约束的几何不变体系。16、是有两个多余约束的几何不变体系。第二章静定结构内力计算(参考答案)1、(O)2、(X)3、(O)4、(O)5、(O)6、(O)7、(X)8、(X)9、(O)10、(X)11、(O)12、(O)13、(O)14、(X)15、(X)16、(O)17、(X)18、(O)19、20、3Pa+1.5m1204040A3m1m80C4020DB40401m.m20M图(kN)21、24、——104——
《结构力学》习题集(上册)Pa2PaPaPa4020M6031、35、2Pa160160401.5Pa253.33.5Pa216.65Pa3PaM图(kN.m)36、39、2PaDC2PaE6PaPaFGPa2Pa2Pa6PaPa3PaPaPaABM图40、41、22qa2qa215F15152qa215151515ECD152qa2AB2qaM图M(kN.m)42、44、——105——
《结构力学》习题集(上册)2ql2/2ql/22Pa/32Pa/32Pa/32ql/22Pa/3BAMM图45、47、10100.5100.50.125101010210(×ql)50、51、PaPaPaPa2PaPaPaPaPa2Pa52、53、N=4.5qa_1175qa2N=9qaqa24.581364.5qa361.5qa24090M图54、55、——106——
《结构力学》习题集(上册)4545444N=-28.8kN364436M(kN.m)56、qa2222qaM57、1512.55551515557.512.5152M图(kN.m)Q(kN)N(kN)58、59、11mPa2m02011m2m020m2Pa0M图61、63、B2qaA2ql8DC23ql2M图64、65、——107——
《结构力学》习题集(上册)PPl0.5Pa0.5PaPPPlM图66、67、46X=30kN5672AXB=18kN3Pl1Pl44PlPlYA=2kN22YB=6kNMN=-P169、70、188818121273、74、1204812075、76、——108——
《结构力学》习题集(上册)406.758021273211168020213130M图(kN.m)M图(kN.m)77、78、P1.5papapa2pa1.5paP2PaPa3pa0.5pa4Pa3012PaPa2P33P/23/2P2P1P335/2P3/2PM图79、H=3kNMK=-2.09kN⋅mNK=-4.098kN80、H=3kN(→←)MK=2kN·mNK=-4.242kN81、MK=15kN⋅m(下拉),Nk=−4.470kNRR82、V=0.5P(↑),H=0.289P(→←),MK=VA(R−)−HA⋅=−0.058PR()2283、N1=0,N2=4P(拉),N3=−5P(压)84、N1=2.5P/3=0.833P(拉),N2=-2P/3=-0.667P(压)85、N1=-P/2(压),N2=-P(压)86、N1=120kN(拉),,N2=0,N3=198kN(拉)87、N1=0,N2=2P88、N1=0,N2=P,N3=2P/289、N2=P,N1=0.6P"="=0反对称情况:N"N"P90、对称情况:N1N21=−2=−2""""N1=N1+N1=−2PN2=N2+N2=2P91、N1=−2P,N2=2.236P92、N1=−0.5P,N2=−P93、N1=5P/2,N2=P94、Na=−20kN——109——
《结构力学》习题集(上册)3595、Na=P,Nb=096、N1=0,N2=-4/3P497、Na=-2P/398、N1=P,N2=−1.414P99、Na=-100kN,Nb=0100、101、12-10-1016-1010160-12160Pl/2Pl/2012N(kN)MN=2P1102、103、40PlPl10330604Pl-28.28.M(kNm)310N(kN)12MN=−22P/3N=−22P/312104、2P/32P/3M图第三章静定结构位移计算(参考答案)1、(X)2、(O)3、(X)4、(C)5、(O)6、(X)7、(O)8、(O)9、(X)37ql10、ϕ=()11、∆DV=140/(EI)(↓)A24EI——110——
《结构力学》习题集(上册)41485312、∆EV=−7ql/(432EI)(↑)13、∆DV=kN⋅m(↓)2EI4ql35ql14、∆BV=↓15、ϕC=()(16EI)()24EI347Pl65qa16、∆DV=(↓)17、∆DV=(↓)24EI24EI4218、∆DV=253ql/384EI(↓)19、ϕAB=4Pl/9EI()2Pl3/EI←→21、Ml()20、3()∆=↓BV2EIH522、∆AB=-8l/3EI(→←)(m)23、∆CH=380(EI)(→)116224、∆BH=272.76/(EI)()25、ϕc=(↓)EI3ql26、∆C=()27、∆DH=2(1+2)PaEA(→)2EI1.414Pa28、∆AB=()EA329、MP=−PRsinθ,M=−R(1−cosθ),∆BH=PR/2EI(→)330、∆DV=8Pa/EI+125Pa/4EA(↓)4231、∆DV=11qa/24EI+15qa/8EA(↓)23Pa32、φSR=()EI−333、∆==6⋅25×10aDV34、∆DV=−∑R⋅c=−a/480(↑)35、∆CH=−∑R⋅∆=−(−1⋅∆)=∆(→)36、∆DV=θl/2+∆/2(↑)37、ϕ=0.025rad()D38、∆=∑αt0Nl=αt(2×2×a/3+1×3×a/4+2×(−5/6)×5×a/4)=0CV——111——
《结构力学》习题集(上册)H39、∆cv=αtl−120αtl=−119αtl(↑)40、∆CD=0.795cm()24Ma41、042、(↑)3EI2343、∆CH=Ml(→)44、∆=5Pl(→)EIDH4EI第四章超静定结构计算——力法(参考答案)1、(1)、4,3;(2)、3;(3)、21;(4)、6;(5)、1;(6)、7;(7)、5,62、(X)3、(O)4、(X)5、(X)6、(X)8、M=31kN⋅m(上侧受拉);M=15kN⋅m(有侧受拉)。ABBC9、X1=2.219(压力)(水平链杆轴力)10、M7M/8M/8X1M/8M11、X=ql(←)(有侧支座水平反力)12、M=2.06kN⋅m(上侧受拉)CB12813、PX1X215、17、——112——
《结构力学》习题集(上册)PlX1PlPlPl2PlPl2Pl2M1图MP图M图332lPlδ11=,∆1P=−,X1=1.5P3EIEI18、M=600kN⋅m(右侧受拉)CA72ql19、四角处弯矩值:M=(外侧受拉)2020、21、2ql/8MPql2/82ql/2X1=1lM223ql/83ql/8M1——113——
《结构力学》习题集(上册)22、l/2P/2P/2l/2X1=1MX11l/2l/2Pl/4Pl/4P/2P/2Pl/4Pl/2MPPl/4M23、.m.m344kN4kN11X13M图(kN.m)24、X1P/2P/21.77P1.77P4.23P3P1.23P3P4.23P1.23P基本体系M图25、11.82210kNX111.82210.445M图(kN.m)10.445——114——
《结构力学》习题集(上册)26、29、141114m(×)2830、MA=MD=Pl/3(上侧受拉)33、X1=NAC=0.561P34、X1=NCB=−0.789P35、N1=2P2,N2=−P2,N3=0,N4=P2036、NDB=NDB+X1=0.086P(拉力)37、M=0。38、Pa2Pa239、3Pl6429Pl64X1M图——115——
《结构力学》习题集(上册)40、X=11M图l3EIθ(4l)41、δX+δX+∆=0,δX+δX+∆=−θ,∆=−c,∆=−c/l.1111121c2112222c1c2c43、6EIc25lM44、6EIC27lX1c/2M图45、644X1=1M1M(´�EIa)46、30EIα/(hl)XM图1——116——
《结构力学》习题集(上册)45αEI48、MB=,下侧受拉h⎛3l5⎞50、∆CV=⎜⋅ϕ−∆⎟(↓)⎝1616⎠1⎛1l13EI⎞3l51、fC=⎜×l××θA⎟=θA(↓)EI⎝242l⎠1652、11PlPl29Pl1P80280X1=11M1图MP图14.5Pl80M图25l−29Pl29Plδ11=,∆1P=,X1=3EI48EI804ql53、∆B=(↓)24EI54、BX1X1=16EIk1=3lqqqA22l2qlkkkk32⎛2ql44ql3⎞⎛l2⎞8l4l3δ11=+∆1P=−⎜+⎟=−2ql⎜+⎟3EIk,⎝EIk⎠⎝EIk⎠,l2+3EIkX1lX1=2qlXδX+∆=−=−X17l411111P1+RE=k6EI1,6EIk,255、1∆X133Xll1δX+∆=−∆,∆==X,δ=,∆=−l,1111∆1111∆kEI3EI——117——
《结构力学》习题集(上册)332lllX13EIX1−l=−X1,(1+3)=1,X1=23EIEI3EI4l3EI4lM图第五章超静定结构计算——位移法(参考答案)1、(1)、4;(2)、4;(3)、9;(4)、5;(5)、7;(6)、7。2、(X)3、(X)4、(O)5、(X)6、(O)7、(O)8、(O)9、(O)10、11、13.515145.522/64)232(×ql(×ql)12、13、pl/469/1041510421/10414/1043.51762/40)()(×qh×Pl14、q=3kN/m15、——118——
《结构力学》习题集(上册)2Z=ql(18)i112ql9Zl121ql21222qlql18ql92ql9Mll320332816、θB=(),∆B=(→)7EI21EI17、10kN20/320/3Z120/310/3Z2M(kNm).18、Z13kN258/72kN/m6120/7162/7M(kN⋅�m)Z219、Z13Z2283156q8111156814(×ql2)20、21、——119——
《结构力学》习题集(上册)25P/2Z17180Z290DCE60P/260BA825M()kN.mM()kNm.22、23、11184441434441M图(×ql2)28M图(kNm).24、Z1Z2q5818189189186189734037818920189M()×ql225、Z60kN/mZ2197.1445.7128.571285.715.7117.14M(kNm.)2.868.5726、——120——
《结构力学》习题集(上册)44730kN/mZ1174Z2298149540447745546298149M(kN.m)27、28、1/23/2Z150/74kN/m75/14Z21/2125/141M图()PlM(kNm).29、30、1/53/101/10221/8.ql1/8.ql(×Pl)31、32、2ql/8Z112411q4885248ql/833、——121——
《结构力学》习题集(上册)51.8513551.8517.8817.8810.7310.735.365.36M(kN.m)36、37、23.5211112M图(ql/7)38、7101010ql2/)(×23340、Z220.7720.7724.33Z120.7720.7715kN24.33M()kNm.41、42、——122——
《结构力学》习题集(上册)3P/23P/22ql362ql722ql3P/23P/29M图(kNm).M43、Z1ql0.410.41ZqEI220.840.5120.842(×ql)44、45、24242412122M(EIc/l11)2M(EI∆/l11)46、iαiαiαiαiα3iα2222+=αα2iα2iα5iα3iα222247、0.7ZZ120.151.30.60.35θ3.65(×iθ)——123——
《结构力学》习题集(上册)912EI48、P=∆325l49、50、542θ176274518M(i∆/3)l(×iθ/5)对称51、52、8265ql5611102ql15562M图M()ql/3253、54、11/61/81/85/61/21/41/41/81/121/41/417/242M()×�PlM图(ql)2klql55、⋅3i/l+2kl8M56、——124——
《结构力学》习题集(上册)57、PZ1Z2k4/51/50M图()×�Pl58、31/120PlPl/649/240PlM图59、M3EI4l60、213ql/32M图第六章超静定结构计算——力矩分配法(参考答案)1、(X)2、(O)3、(X)4、(O)5、(O)6、(O)7、(O)8、18334.5(kN·m)9、RB=8kN——125——
《结构力学》习题集(上册)10、M=3Pl(下侧受拉)AD511、M=1.67kN⋅m(下侧受拉),M=11.67kN⋅m(上侧受拉),ABBCM=3.63kN⋅m(上侧受拉)CD12、M=11.63kN⋅m(下侧受拉),M=23.25kN⋅m(上侧受拉),ABBCM=13.97kN⋅m(上侧受拉)CD13、µBA=1/3,µBC=2/3,µCB=1,µCD=0,FFFFMBA=40kN·m,MBC=8kN·m,MCB=16kN·m,MCD=-16kN·m15、41.8542.2910.73844821.5241.93M(kN.m)16、m225mm147mmmm5m717、18、28.8661012.825.612024120G6.4ABC48.m(kN·m)M(kN)——126——
《结构力学》习题集(上册)19、20、117.947619.4822.175269.2352.83141038.9813.39267M()kN.mM图(kN.m)FF21、µAB=0.103,µAC=0.619,µAD=0.278,MBA=18kN⋅m,MAB=36kN⋅m,FFFFMAD=−30kN⋅m,MDA=0,MCA=0,MAC=0FF22、µAB=0.375,µAC=0.125,µAD=0.5,MBA=0,MAB=60kN⋅m,FFFFMAD=−50kN⋅m,MDA=50kN⋅m,MCA=0,MAC=023、24、402097.5201.51.510.510M(kNm).0.75(kN⋅m)26、M=4.5kN⋅m(上侧受拉),M=1.5kN⋅m(上侧受拉)ABAD53018FFF2027、µAB=,µAC=,µAD=,MAD=10kN·m,-MAC=MCA=kN·m535353330、73.7232.5736.8514.5732.57(kN⋅m)——127——
《结构力学》习题集(上册)31、47.0830.8330.832020ADC10.8410.8423.5523.55B5.425.42,,M()kNm.34、35、92010kN53101561105q5(kN·m)(×)936、37、4.471.956i∆l4.542.606i5.23l∆i∆M()lM图38、M=37.9kN⋅m(上侧受拉),M=4.9kN⋅m(下侧受拉),ABBCM=54.7kN⋅m(下侧受拉),M=79.9kN⋅m(上侧受拉)CDDC40、0.533M0.133M0.267M0.467MM图——128——
《结构力学》习题集(上册)第七章影响线及其应用(参考答案)1、(O)2、(O)7、l/2lMA影响线8、(1)MC影响线(2)QC右影响线3EFG2DD1/2EFG3/49、MB影响线10、MA影响线(设内侧受位为正)BCDABDE4mA11、12、lMC1QF1x13、Na=−114、V3影响线d4aAC——129——
《结构力学》习题集(上册)Q16、C影响线17、MA影响线右1/21m+EFGH2mM=0A18、MA4mMA=-520kNm19、11+QCACDEFG1QC=70kN20、RB影响线21132R=72kN。Bmax21、RB影响线3kN3kN1kN1333/25/413/4+A"BDCR=8.625KNBmax第八章矩阵位移法(参考答案)1、(O)2、(X)3、(O)4、(X)5、(X)6、(O)7、(O)8、(X)9、(O)10、(O)11、(A)——130——
《结构力学》习题集(上册)212、K=36i/l+k,k=EA/l,K=12i,i=EI/l,K=4i2233133213、K22=EA/l+12EI/l,K34=6EI/l,K15=0314、K44=3EA/l,K55=36EI/l+4EA/l,K66=12EI/l①②③③15、[K22]=[K22]+[K22]+[K22],[K24]=[K21]⎛2⎞EA2EA16、K77=⎜⎜+1⎟⎟,K78=−⎝4⎠l4l317、K11=288EI/l,K88=20EI/l(4,5,0)(7,8,0)2(4,5,6)②3(7,8,9)①③12EIEA1(1,2,3)4(10,11,12)18、K=+K45=0443ll19、⎡4(i1+i2)2i20⎤⎢⎥[K]=⎢2i24(i2+i3)2i3⎥⎢02i4i⎥⎣33⎦⎡8i4i00⎤⎢⎥12i2i0⎢⎥20、[K]=,i=EI/l⎢对16i6i⎥⎢⎥⎢⎣称12i⎥⎦⎡K①+K③K③⎤[22][22][21]21、[K]=⎢⎥⎢③③②④⎥⎢⎣[K12][K11]+[K22]+[K22]⎥⎦22、2⎡36i/l−6i/l6i/l⎤⎢⎥EI[K]=⎢对12i2i⎥,式中:i=⎢⎥l⎢⎣称4i⎥⎦——131——
《结构力学》习题集(上册)⎡36EI⎤23、[K]=⎢3⎥⎣l⎦24、25、::3(0,0,0)3(0,0,0)1(0,0,0)6(1,0,4)2(0,0,0)1(0,0,0)2(0,0,0)4(1,0,2)5(1,0,3)5(1,2,0)4(1,2,3)⎡⎛2EA12EI⎞-6EI⎤⎡2EI⎤⎢⎜+3⎟002⎥⎢00⎥⎢⎝ll⎠l⎥l⎢⎥⎢4EI00⎥⎢⎛36EIEA⎞−6EI⎥⎢⎥[K]=⎜+⎟[K]=l⎢l3ll2⎥⎢⎥⎝⎠⎢4EI⎥⎢⎥⎢0⎥⎢12EI⎥⎢l⎥⎢⎥⎣l⎦⎢4EI⎥⎢⎣l⎥⎦⎡k①+k②k②⎤22111226、、⎢②②③⎥⎢⎣k21k22+k22⎥⎦27、1(0,1)(0,1)③①⎡22+11−1⎤(0,0)2EA⎢⎥2②(2,3)[K]=×⎢122+1−1⎥34l⎢⎥(0,0)−1−11(2,3)⎣⎦28、⎡612030⎤4⎢⎥[K]=10×⎢03240⎥⎢⎣300300⎥⎦⎧2kN⎫⎧ql/2⎫⎪⎪⎪⎪29、{P3E}=⎨−12kN⎬30、{P2E}=⎨−ql/2⎬⎪⎩2kN⋅m⎪⎭⎪−ql224⎪⎩⎭——132——
《结构力学》习题集(上册)2⎧−ql/24⎫⎪⎪2⎧−ql⎫⎪25ql/24⎪31、{P2E}=⎨2⎬32、{P}=⎨2⎬⎩ql/24⎭⎪−ql/24⎪⎪2⎪⎩ql/8⎭T2233、{P}=[(−M−Pl/8)(Pl/8−ql/12)ql/12]T34、{P}=[7−340]35、⎧−2kN⎫(0,0)(0,0){}⎪−5kN⋅m⎪(1,2)(0,3)P=⎨⎬⎪⎩−16kN⋅m⎪⎭2236、P1=ql,P3=ql/24,P4=−ql⎧ql/2⎫⎪⎪37、{P}=⎨−ql/2⎬⎪2⎪⎩25ql/24⎭238、P4=ql/2,P5=−ql/2,P6=ql/12239、P=−pl8,P=−P−ql2,P=M−Pl8+ql12113341240、2685、P3=11ql/12,P7=−ql/2,P8=−ql/2,P9=0T41、{P}=[6−22−145−1218]T42、{P}=[−41040−6−4]⎧P/2⎫⎪⎪43、{P2}=⎨−3P/2⎬⎪⎪⎩−3Pl/4⎭44、——133——
《结构力学》习题集(上册)1(0,0,0)⎧−3kN⎫3(1,4,3)⎪⎪2(1,2,3)⎪−8kN⎪{P}=⎨⎬−17kN⋅m⎪⎪⎪0⎪4(0,0,0)⎩⎭45、⎧0⎫⎪2⎪⎪11ql/12⎪⎪⎪ql/2⎪⎪(1,0,2)(3,4,5){P}=⎨⎬−3ql⎪⎪(0,6,0,)⎪ql2/8⎪⎪⎪(0,0,0)⎪⎩−ql/2⎪⎭T46、{P}=[40-32-14]⎧10kN⎫⎪⎪47、{P}=⎨−10kN⎬⎪⎩−10kN⋅m⎪⎭T2⎡PqlqlPl⎤48、{P}=⎢0,0,−,−,+⎥⎣22128⎦⎧8kN⎫49、{P}=⎨⎬⎩6kN⎭T50、{P}=[10,−20,30,−40]kN51、S=F=−0.43196652、N14=−0.0587kN53、F2=0.2336kN54、F3=0.333kN⋅m,F6=−0.333kN⋅m①T55、{F}=[−85.581kN85.581kN]56、3P(压力)②57、M2=−89.25kN——134——
《结构力学》习题集(上册)①58、N=3P(压力)59、⎧−5kN⎫⎪⎪{}①⎪0⎪F=⎨⎬⎪5kN⎪⎪⎩0⎪⎭60、⎧19.3kN⎫⎪⎪−19.726kN⎪⎪③⎪⎪−651.561kN.m⎪⎪{F}=⎨⎬−19.3kN⎪⎪⎪19.726kN⎪⎪⎪⎪⎩−1321kN.m⎪⎭61、⎧11.1006kN⎫⎪⎪10.1302kN⎪⎪{}①⎪⎪−4.0385kN⋅m⎪⎪F=⎨⎬⎪−11.1006kN⎪⎪13.8698kN⎪⎪⎪⎪⎩13.3873kN⋅m⎪⎭62、⎧0⎫⎪⎪0.79ql⎪⎪①⎪⎪0.234ql2⎪⎪{F}=⎨⎬(7分)0⎪⎪⎪0.208ql⎪⎪⎪2⎪⎩0.0575ql⎪⎭63、RB=0.67857ql(↑)第九章结构的动力计算(参考答案)1、(X)2、(X)3、(X)4、(X)5、(O)6、(O)7、(O)8、(X)9、(X)——135——
《结构力学》习题集(上册)310、ω=192EIg/5Wl11、ω=(4kg/W)32312、δ=3l/48EI,ω=16EI/(ml)1132313、δ=5l/48EI,ω=48EI/(5ml)14、24EIEIω==1.4773311mlml32315、δ=5l/3EI,ω=3EI/(5ml)329EI16、k=9EI/l,ω=113mlEI232317、ω=1.5,(24EI−4mωl)A−6mωlA=0,1312mlEI2323ω=4.28,3mωlA+(8mωl−24EI)A=02312ml110.451.10.451.11.112−118、ω=54.2s319、T=2π(Wh/6EIg)320、T=2π(Wh/48EIg)321、ω=2.889EI/(ma)——136——
《结构力学》习题集(上册)22、ω:ω=1:2ab23、T=16.56(W/EAg)24、ω=1/mδ=EA/10.5m-122ω=(EI/8ml/2)=24.25s,µ=1/(1−θ/ω)=3.127,25、M=µ,Y=µYstp=1.3029cmDmaxMstpMax−12226、ω=1/mδ=1/m(4/3EI+1/4k)=34.16sµ=1/(1−θ/ω)=1.522Y=µy=0.006m,,M=µM=7.61kNm,DmaxstpDmaxstp27、2PY=P/mω,µ=1.04067,Y=Asin(ωt)+Bcos(ωt)+µcos(θt),stD2DmωθA=Yµ,B=l/1000,stDωY=0.001lcos(ωt)−0.20833Ysin(ωt)+1.04167Ysin(θt),stst28、27/(3)θ=EIml-1-1329、ω=38.92s,θ=15.71s,µ=1.19,y=2.09/10mmax-1−430、θ=52.36s,β=1.378,,y=1.9610m,A=βy=0.27mmststM=βFM=2.756MD-1-131、ω=71.50s,θ=62.83s,;β=4.389;A=βFδ=3.37mm;y=(w+βF)δ=5.28mmmax-132、θ=57.596s,β=1.496,MD=βFM=7.48M,{}TM=M+M=15.480.52MmaxstD3EI3EI33、ω=,k=,33mll——137——
《结构力学》习题集(上册)25P运动方程:m�y�+ky=k⋅∆,�y�+ωy=1P16m*特征解y:*5P01P0y=sinθt=0.0595sinθt2216mωθm1−2ω*PlP0l()M=m�y�l+=(0.0595Pl+)sinθt=0.56Plsinθt,M=0.56PlA00Amax0223EI5Psin(θt)34、m�y�+y=3l1635、3−PlY=Pl/4EI,µ=4/3,Y=(sit(θt))st3EIPPl/1213Pl/2423T36、λ=1/ω=ma{3.21230.1211}/EI33ω=0.558(EI/ma),ω=2.874(EI/ma)1223T37、λ=1/ω=ma{0.1259840.07350}/EI33ω=0.8909(EI/ma),ω=3.6886|(EI/ma)12Y/Y=1/0.954,Y/Y=1/(−2.097)112112223338、δ=δ=2a/3EI,δ=a/6EI,11221233ω=1.0954(EI/ma),ω=1.414(EI/ma)1223Tλ=1/ω=ma{5/61/2}/EI,Y11/Y21=1/1,Y12/Y22=1/(−1)——138——
《结构力学》习题集(上册)aa11MM21111139、4821m⎧8.554⎫δ11=,δ22=,δ12=−λ=2=EI⎨0.779⎬3EIEIEI,ω⎩⎭EIEIω=0.3419,ω=1.132812mm331/240、对称:δ=5l/162EI,ω=5.69(EI/ml),1331/2反对称:δ=0.00198l/EI,ω=22.46(EI/ml),233341、δ=5l/48EI,δ=l/24EI,δ=δ=5l/96EI1122122133ω=2.736EI/ml,ω=9.054EI/ml12T{Φ1}=[10.565],(3分)0.56511.766T{Φ2}=[1−1.766](3分)1331/242、对称:δ=5l/24EI,ω=2.191(EI/ml),112333反对称:δ11=4l/EI,δ21=δ12=l/8EI,δ22=l/48EI,31/2ω=0.5(EI/ml),131/2ω=7.69(EI/ml),2——139——
《结构力学》习题集(上册)TTT{Y1}=[10.03-0.03],{Y2}=[011],,{Y3}=[1-31.8631.86]EIEI43、ω1=1.23,ω2=8.23,mlml333l2llδ=,δ=,δ=δ=,1122122148EI38EI16EIY111Y121=,=−Y10.4Y0.12122λ1⎡1.07⎤3ω1⎡0.97⎤344、=⎢⎥ma/EI;=⎢⎥EI/maλ0.0975ω3.22⎣⎦2⎣⎦(1)(1)(2)(2)A/A=−0.28;A/A=+3.611212345、ω=48EI/ml46、δ=4.5/(EI),δ=1/(EI),δ=δ=−1.6875/(EI),11221221λ=5.1818m/(EI),λ=0.3189m/(EI),12ω=0.4393(EI)/m,ω=1.7708(EI/m),1247、δ=14/(3EI),δ=δ=−4/(EI),δ=32/(3EI)11122122λ=12.6645m/(EI),λ=2.6664m/(EI)12ω=0.281(EI/m),ω=0.6124(EI/m)12Φ:Φ=1:−2,Φ:Φ=1:0.5112112223348、ω=10.47EI/ml,ω=13.86EI/ml,1249、k11=2k,k22=k,k12=k21=−k2k⎧2.2808⎫kkω=⎨⎬,ω1=0.4682,ω2=1.5102m⎩0.2192⎭mmY1Y11112=,=Y1.781Y−0.281212222250、k11=6i/l,k21=k12=−6i/l,k22=30i/l,——140——
《结构力学》习题集(上册)ω=0.146(EI/m)1/2,1/21ω2=0.381(EI/ml),{}[]T{}[]TΦ=10.236,Φ=1-4.241233351、k11=18EI/l,k12=−12EI/l,k22=99EI/8l,EIEIω=1.692,ω=5.2451323mlml52、利用对称性:3l6EIEI反对称:δ11=,ω1=3=2.453,6EImlml3l96EIEI对称:δ11=,ω2=3=3.7396EI7mlml53、列幅值方程:2222δ2mωx+δ2mωy=x⎫2mωδ−1δmω11121112⎬,=0,2222δ2mωx+δ2mωy=y2mωδδmω−12122⎭2111333ll4lδ=,δ=δ=,δ=111221223EI2EI3EI2x2δ11δmωxmmωx1122yδ21δ22mωy13aEI54、对称:δ22=0.1833,ω2=3.30323EIma34aEI反对称:δ11=,ω1=0.70713EIma55、对称:11δ=a3/(24EI),ω=24EI/(ma3)111反对称:11δ=7a3/(768EI),ω=768EI/(7ma3)111——141——
《结构力学》习题集(上册)3356、ω1=0.648EI/ml,ω2=7.92EI/ml57、3设k=24EI/l频率方程:(2)(2)224222k()3k−ωmk−ωm−k=0,mω−4kmω+2k=0,ω=2±2mω:ω=0.1716:1=1:5.8281212EI48EIΦΦ111258、ω1=4,ω2=4,=0.5,=−1mlmlΦΦ21223EI3EI51EI59、k11=3,k12=−3,k22=3lll⎡10⎤EIEI⎡11⎤[M]=⎢⎥m,ω1=1.6733,ω2=5.073,[Φ]=⎢⎥⎣02⎦mlml⎣14.02−0.132⎦60、ω=0.379EAg/W,ω=0.506EAg/W1261、ω1=0.34EA/m,ω2=0.48EA/m62、33l5lδ=,δ=,111224EI48EI3A0.05313l⎧1⎫⎧⎫Plδ22=,⎨⎬=⎨⎬3EI⎩A2⎭⎩0.1397⎭EI0.61332Pl0.047612Pl63、482424A0.05383EIEIEI⎧1⎫⎧⎫Phk11=3,k22=3,k12=−3,⎨⎬=⎨⎬hhh⎩A2⎭⎩0.0500⎭EI——142——
《结构力学》习题集(上册)0.0252Ph0.3220Ph0.347Ph8−164、反对称结构:δ=,ω=34.641s,µ=1.5762EI两竖杆下端动弯矩为31.524kN⋅m,左侧受拉。65、333δ=l=3EI,δ=5l/6EI,δ=8l/3EI,11122233δ=4l/3EI,δ=14l/3EI,1323233ω=0.1382EI/(ml),δ=9l/EI,1332ω(δmA+δmA+δmA)=Ai1111i1222i1333i1i第十章结构弹性稳定计算1、(X)2、(X)3、(X)4、(O)5、(O)6、(O)7、2(1−cosαl)=αl⋅sinαl.1⎛Pk⎞⎛kl⎞8、⎜−⎟sinαl+⎜−1⎟cosαl=0α⎝kϕP⎠⎝P⎠αkrkr6n9、tgαl===,αl⋅tgαl=6npαEIαl10、P1cr=0.586kl,P2cr=3.414klkr6EI11、Pcr==2ll2πEI12、Pcr=2(2l)——143——
《结构力学》习题集(上册)22πEIπEI13、=kl,K=。2min3ll222πEI14、cosnl+sinnl=0,nl=π/2Pcr=2。4l2πEI15、P=cr23hπ16、l0=l=1.987l.1.584EI17、Π=0,Pcr=lH2⎛u⎞2πEI18、Pcr=⎜⎟=2.⎝λ⎠lmin574EIl4l42EI19、−P=0,Pcr=25210l第十一章结构的极限荷载1、(X)2、(O)3、(O)4、(O)5、(O)6、(X)7、Mu=Mu(铰B单向转动)P8、Mu=2Mua2l9、x=,Pu=Mu2ab10、极限状态为:PPuuPu()a()b()c22bhbh11、Mu=σy,Pu=0.75σy4l12、Pu=60kNMu13、Pu=9=135kNlMu14、qu=162l——144——
《结构力学》习题集(上册)15Mu15、Pu=。2l2Pl/15Pl/102Pl/15Pl/10Mu16、qu=2a17、Pu=6.25kN18、Pu=22.1kN20206.851.420M图(kN.m)19、Pu=1.3Mu/lMu0.2Mu0.4MuMMuuMu20、Pu=4.5l21、(1)6Pl/48PACDB9Pl/48l/2l/2l/2µ2/31/3MF-3Pl/1600+6Pl/48+3Pl/48M0+6Pl/48-6Pl/4809Pl16Mu令MD=Mu得屈服荷载=Mu,Py=。483l——145——
《结构力学》习题集(上册)(2)PuMu2Mu6MuP=ul9Mu22、q=u2l6Mu23、Pu=l24、Mu=1.8q4Mu25、Pu=l6.964126、qu=2Mul4Mu27、P=ul28、qu=0.5Mu4029、Mu==23.53kN⋅m1.730、Pu=32.7kN,作用在C点。31、qu=40kN/mMu32、qu=11.662,BC跨先破坏。l33、qu=25.54kN/m,塑性铰在B处和距A点3.31m处。34、Pu=2.6Mu/a7Mu35Pu=636、Pu=5kN12Mu37、对称性取半结构,Pu=l38、Pu=Mu/a——146——
《结构力学》习题集(上册)PPθθ122θ3θ39、PMθu2θMu2MMuuθ1.5MuθMθuMMu(a)u(b)1l+2(a)联合机构:q⋅⋅l⋅l⋅θ+P⋅⋅θ=Mu⋅θ+2Mu×2θ,q1=5Mu/l,221+22(b)侧移机构:q⋅⋅l⋅lθ=Mu(θ+θ),q2=4Mu/l,qu=4Mu/l240、θMuMMuuθθ2θ2θMMuuθMu(a)梁机构(b)联合机构+1l+16Muq×⋅l⋅⋅θ=Mu(θ+θ+2θ),q=222l22lqlPlθ+q⋅⋅θ=Mu(θ+θ+2θ),(Pl+)θ=5Muθ44M16Muu内力可接受Pu=,或qu=2ll3Mu41、在截面B和D处出现塑性铰时,Pu=a1当A、D处出现塑性铰时,Pu=(Mu′+3Mu)2a——147——'
您可能关注的文档
- 合集:《健康评估-学习指导与习题集》:.doc
- 吉大11春学期《新视野英语(三)》复习题及答案.doc
- 吉林大学离散数学课后习题答案.doc
- 吉林电子信息职业技术学院2012年《关系数据库与SQL Server 2005》习题参考答案.doc
- 同济-线性代数第五版(课后全部答案).pdf
- 同济大学《建筑混凝土结构设计》习题解答汇总2014-6-24.pdf
- 同济大学《高等数学》第3版下册答案.doc
- 同济大学《高等数学》第三版下册答案.doc
- 同济大学《高等数学》第五版下册答案 2.doc
- 同济大学朱慈勉 结构力学 第5章习题答案.doc
- 同济大学朱慈勉 结构力学 第6章习题答案.doc
- 同济大学第3版《高等数学》下册答案.doc
- 同济大学第六版高等数学上下册课后答案全集.pdf
- 同济大学第六版高等数学课后答案全集.pdf
- 同济大学结构力学习题答案-朱慈勉.pdf
- 同济大学钢结构基本原理(沈祖炎)课后习题答案完全版.doc
- 同济大学顾祥林 混凝土结构课后答案.pdf
- 同济第六版(高等数学课后习题解答)下册.pdf