- 2.02 MB
- 2022-04-29 14:15:07 发布
- 1、本文档共5页,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,可选择认领,认领后既往收益都归您。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细先通过免费阅读内容等途径辨别内容交易风险。如存在严重挂羊头卖狗肉之情形,可联系本站下载客服投诉处理。
- 文档侵权举报电话:19940600175。
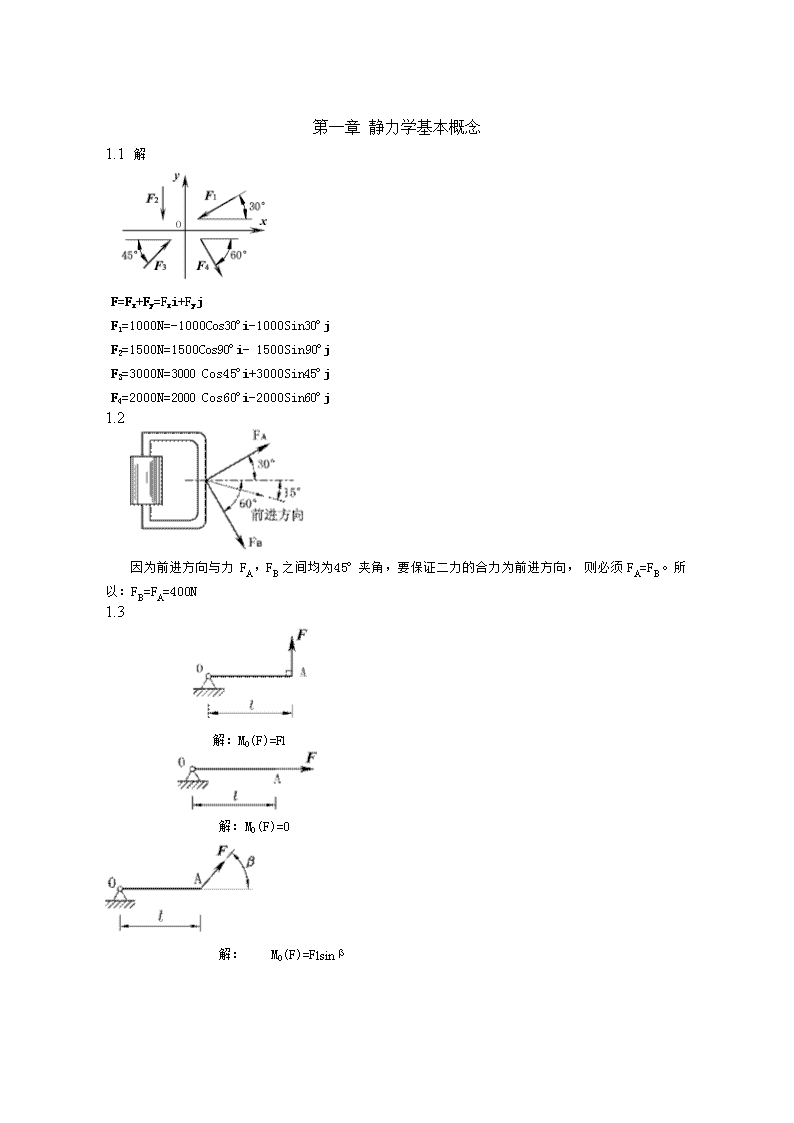
'第一章静力学基本概念1.1解F=Fx+Fy=Fxi+FyjF1=1000N=-1000Cos30ºi-1000Sin30ºjF2=1500N=1500Cos90ºi-1500Sin90ºjF3=3000N=3000Cos45ºi+3000Sin45ºjF4=2000N=2000Cos60ºi-2000Sin60ºj1.2因为前进方向与力FA,FB之间均为45º夹角,要保证二力的合力为前进方向,则必须FA=FB。所以:FB=FA=400N1.3解:MO(F)=Fl解:MO(F)=0解:MO(F)=Flsinβ
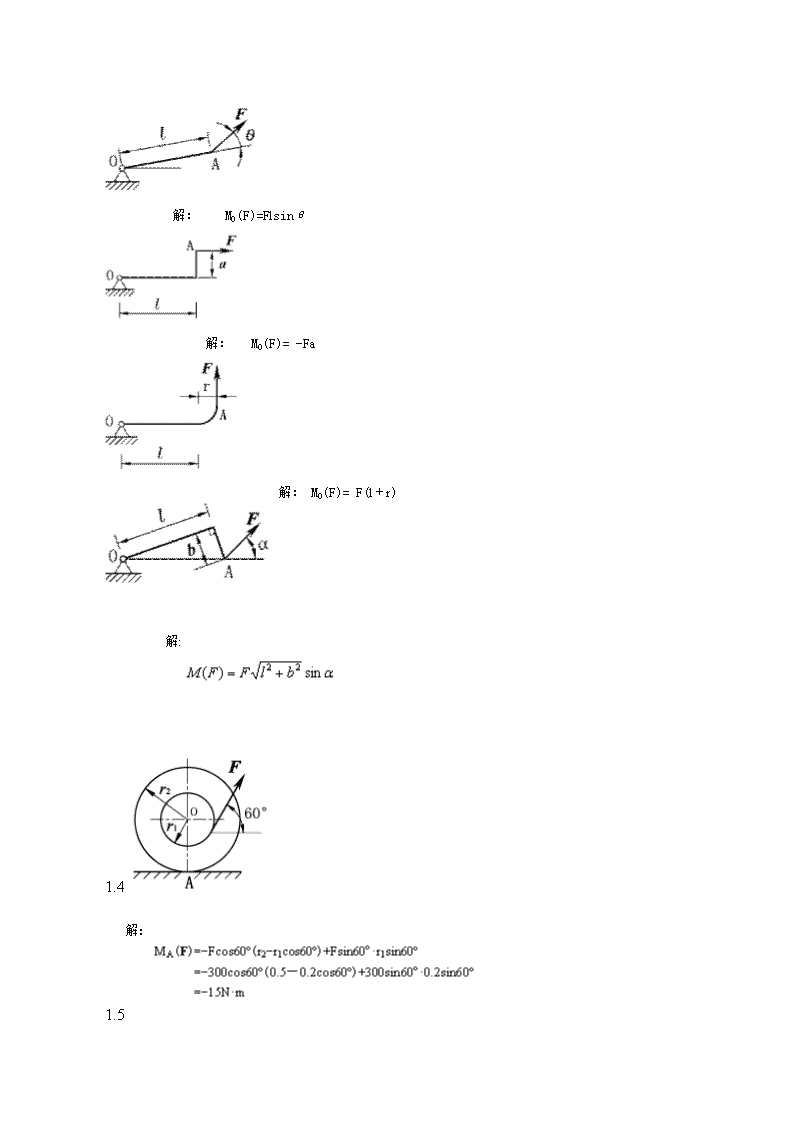
解:MO(F)=Flsinθ解:MO(F)=-Fa解:MO(F)=F(l+r)解:1.4解:1.5
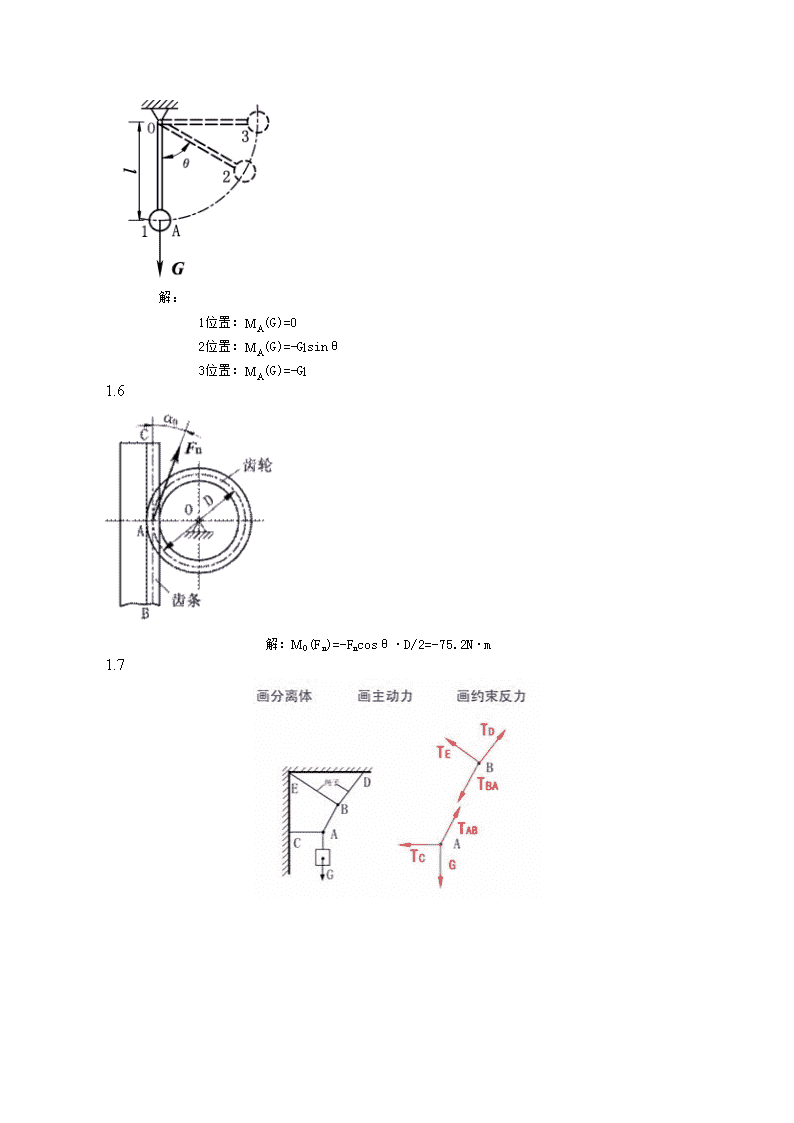
解:1位置:MA(G)=02位置:MA(G)=-Glsinθ3位置:MA(G)=-Gl1.6解:MO(Fn)=-Fncosθ·D/2=-75.2N·m1.7
1.8
第二章平面力系2.1力系简化解:(1)主矢大小与方位:F/Rx=∑Fx=F1cos45º+F3+F4cos60º=100Ncos45º+200N+250cos60º=395.7NF/Ry=∑Fy=F1sin45º-F2-F4sin60º=100Nsin45º-150N-250sin60º=-295.8N
(2)主矩大小和转向:MO=∑MO(F)=MO(F1)+MO(F2)+MO(F3)+MO(F4)+m=0-F2×0.3m+F3×0.2m+F4sin60×0.1m+F×0.1m=0-150N×0.3m+200N×0.2m+250Nsin60×0.1m+50N×0.1m=21.65N·m(Q)向O点的简化结果如图所示。2.2起吊重量解:根据O点所能承受的最大力偶矩确定最大起吊重量G×0.15m=5kN·mG=33.33kN2.3求支架的力A图:解:(1)取销钉A画受力图如图所示。AB、AC杆均为二力杆。(2)建直角坐标系,列平衡方程:∑Fx=0,-FAB+FACcos60°=0∑Fy=0,FACsin60°-G=0(3)求解未知量。FAB=0.577G(拉)FAC=1.155G(压)
B图:解(1)取销钉A画受力图如图所示。AB、AC杆均为二力杆。(2)建直角坐标系,列平衡方程:∑Fx=0,FAB-FACcos60°=0∑Fy=0,FACsin60°-G=0(3)求解未知量。FAB=0.577G(压)FAC=1.155G(拉)C图:解(1)取销钉A画受力图如图所示。AB、AC杆均为二力杆。(2)建直角坐标系,列平衡方程:∑Fx=0,-FAB+Gsin30°=0∑Fy=0,FAC-Gcos30°=0(3)求解未知量。FAB=0.5G(拉)FAC=0.866G(压)D图:解(1)取销钉A画受力图如图所示。AB、AC杆均为二力杆。(2)建直角坐标系,列平衡方程:∑Fx=0,-FABsin30°+FACsin30°=0∑Fy=0,FABcos30°+FACcos30°-G=0(3)求解未知量。FAB=FAC=0.577G(拉)
2.4约束力解(1)取圆柱A画受力图如图所示。AB、AC绳子拉力大小分别等于G1,G2。(2)建直角坐标系,列平衡方程:∑Fx=0,-G1+G2cosα=0∑Fy=0,FN+G2sinα-G=0(3)求解未知量。2.5求滚轮A,B所受到的压力解(1)取翻罐笼画受力图如图所示。(2)建直角坐标系,列平衡方程:∑Fx=0,FNAsinα-FNBsinβ=0∑Fy=0,FNAcosα+FNBcosβ-G=0(3)求解未知量与讨论。将已知条件G=3kN,α=30°,β=45°分别代入平衡方程,解得:FNA=2.2kNFNA=1.55kN有人认为FNA=Gcosα,FNB=Gcosβ是不正确的,只有在α=β=45°的情况下才正确。
2.6求AB和AC所受的力A图:解(1)取滑轮画受力图如图所示。AB、AC杆均为二力杆。(2)建直角坐标系如图,列平衡方程:∑Fx=0,-FAB-Fsin45°+Fcos60°=0∑Fy=0,-FAC-Fsin60°-Fcos45°=0(3)求解未知量。将已知条件F=G=2kN代入平衡方程,解得:FAB=-0.414kN(压)FAC=-3.15kN(压)B图:解:(1)取滑轮画受力图如图所示。AB、AC杆均为二力杆。(2)建直角坐标系如图,列平衡方程:∑Fx=0,-FAB-FACcos45°-Fsin30°=0∑Fy=0,-FACsin45°-Fcos30°-F=0(3)求解未知量。将已知条件F=G=2kN代入平衡方程,解得:FAB=2.73kN(拉)FAC=-5.28kN(压)2.7求挡板所受的压力解(1)取两圆管画受力图如图所示。
(2)建直角坐标系如图,列平衡方程:∑Fx=0,FNcos30°-Gsin30°-Gsin30°=0(3)求解未知量。将已知条件G=4kN代入平衡方程,解得:FN=4.61kN若改用垂直于斜面上的挡板,这时的受力上图右建直角坐标系如图,列平衡方程:∑Fx=0,FN-Gsin30°-Gsin30°=0解得:FN=4kN2.8求支座A,B处的约束力A图:解(1)取AB杆画受力图如图所示。支座A,B约束反力构成一力偶。(2)列平衡方程:∑Mi=015kN·m-24kN·m+FA×6m=0(3)求解未知量。FA=1.5kN(↓)FB=1.5kN(↑)B图:解(1)取AB杆画受力图如图所示。支座A,B约束反力构成一力偶。(2)列平衡方程:∑Mi=0,FA×lsin45°-F×a=0(3)求解未知量。C图:解(1)取AB杆画受力图如图所示。支座A,B约束反力构成一力偶。
(2)列平衡方程:∑Mi=0,20kN×5m-50kN×3m+FA×2m=0(3)求解未知量。FA=25kN(↓)FB=25kN(↑)2.9求螺栓A,B,C,D所受的力解螺栓A,B受力大小(1)取电动机画受力图如图所示。螺栓A,B反力构成一力偶。(2)列平衡方程:∑Mi=0,-M+FA×a=0(3)求解未知量。将已知条件M=20kN·m,a=0.3m代入平衡方程,解得:FA=FB=66.7kN螺栓C,D受力大小(1)取电动机和角架画受力图如图所示。螺栓C,D反力构成一力偶。(2)列平衡方程:∑Mi=0,-M+FC×b=0(3)求解未知量。将已知条件M=20kN·m,b=0.6m代入平衡方程,解得:FC=FD=33.3kN2.10求连杆AB所受的力解
求连杆AB受力(1)取曲柄OA画受力图如图所示。连杆AB为二力杆。(2)列平衡方程:∑Mi=0,-M1+FAB×OAsin30º=0(3)求解未知量。将已知条件M1=1N·m,OA=0.4m,代入平衡方程,解得:FAB=5N;AB杆受拉。求力偶矩M2的大小(1)取铰链四连杆机构OABO1画受力图如图所示。FO和FO1构成力偶。(2)列平衡方程:∑Mi=0,-M1+M2-FO×(O1B-OAsin30º)=0(3)求解未知量。将已知条件M1=1N·m,OA=0.4m,O1B=0.6m代入平衡方程,解得:M2=3N·m2.11求钢绳拉力F和A,B的反力解(1)取上料小车画受力图如图所示。(2)建直角坐标系如图,列平衡方程:∑Fx=0,F-Gsinα=0∑Fy=0,FNA+FNB-Gcosα=0∑MC(F)=0,-F×(d-e)-FNA×a+FNB×b=0(3)求解未知量。将已知条件G=240kN,a=1m,b=1.4m,e=1m,d=1.4m,α=55°代入平衡方程,解得:FNA=47.53kN;FNB=90.12kN;F=196.6kN2.12求立柱A端的约束反力
解(1)取厂房立柱画受力图如图所示。A端为固定端支座。(2)建直角坐标系如图,列平衡方程:∑Fx=0,q×h-FAx=0∑Fy=0,FAy-G-F=0∑MA(F)=0,-q×h×h/2-F×a+MA=0(3)求解未知量。将已知条件F=60kN,q=2kN/m,G=40kN,a=0.5m,h=10m代入平衡方程,解得:FAx=20kN(←);FAy=100kN(↑);MA=130kN·m(Q)2.13求图示梁的支座反力A图:解(1)取梁AB画受力图如图所示。(2)建直角坐标系,列平衡方程:∑Fx=0,FAx-Fcos45º=0∑Fy=0,FAy-Fsin45º+FNB=0∑MA(F)=0,-Fsin45º×2m+FNB×6m=0(3)求解未知量。将已知条件F=6kN代入平衡方程。解得:FAx=4.24kN(→);FAy=2.83kN(↑);FNB=1.41kN(↑)。B图:解(1)取梁AB画受力图如图所示。(2)建直角坐标系,列平衡方程:∑Fx=0,FAx-Fcos30º=0∑Fy=0,FAy-q×1m-Fsin30º=0
∑MA(F)=0,-q×1m×1.5m-Fsin30º×1m+MA=0(3)求解未知量。将已知条件F=6kN,q=2kN/m代入平衡方程,解得:FAx=5.2kN(→);FAy=5kN(↑);MA=6kN·m(Q)。C图:解(1)取梁AB画受力图如图所示。因无水平主动力存在,A铰无水平反力。(2)建直角坐标系,列平衡方程:∑Fy=0,FA-q×2m+FB=0∑MA(F)=0,-q×2m×2m+FB×3m+M=0(3)求解未知量。将已知条件q=2kN/m,M=2kN·m代入平衡方程,解得:FA=2kN(↑);FB=2kN(↑)。D图:解(1)取梁AB画受力图如图所示。(2)建直角坐标系,列平衡方程:∑Fx=0,FAx-q×a=0∑Fy=0,FAy=0∑MA(F)=0,-q×a×0.5a+MA=0(3)求解未知量。将已知条件q=2kN/m,M=2kN·m,a=1m代入平衡方程,解得:FAx=2kN(→);FAy=0;MA=1kN·m(Q)。E图:解(1)取梁AB画受力图如图所示。因无水平主动力存在,A铰无水平反力。(2)建直角坐标系,列平衡方程:
∑Fy=0,FA-q×a+FB-F=0∑MA(F)=0,q×a×0.5a+FB×2a-M-F×3a=0(3)求解未知量。将已知条件F=6kN,q=2kN/m,M=2kN·m,a=1m代入平衡方程,解得:FA=-1.5kN(↓);FB=9.5kN(↑)。F图:解(1)取梁AB画受力图如图所示。(2)建直角坐标系,列平衡方程:∑Fx=0,FA-FBx=0∑Fy=0,FBy-F=0∑MB(F)=0,-FA×a+F×a+M=0(3)求解未知量。将已知条件F=6kN,M=2kN·m,a=1m代入平衡方程,解得:FA=8kN(→);FBx=8kN(←);FBy=6kN(↑)。G图:解(1)取梁AB画受力图如图所示。(2)建直角坐标系如图,列平衡方程:∑Fx=0,FAx-FBsin30º=0∑Fy=0,FAy-F+FBcos30º=0∑MA(F)=0,-F×a-FBsin30º×a+FBcos30º×2a+M=0(3)求解未知量。将已知条件F=6kN,M=2kN·m,a=1m代入平衡方程,解得:FB=3.25kN(↖);FAx=1.63kN(→);FAy=3.19kN(↑)。H图:解:求解顺序:先解CD部分再解AC部分。解CD部分(1)取梁CD画受力图如图所示。(2)建直角坐标系,列平衡方程:∑Fy=0,FC-F+FD=0∑MC(F)=0,-F×a+FD×2a=0
(3)求解未知量。将已知条件F=6kN代入平衡方程,解得:FC=3kN;FD=3kN(↑)解AC部分(1)取梁AC画受力图如图所示。(2)建直角坐标系,列平衡方程:∑Fy=0,-F/C-FA+FB=0∑MA(F)=0,-F/C×2a+FB×a=0(3)求解未知量。将已知条件F/C=FC=3kN代入平衡方程,解得:FB=6kN(↑);FA=3kN(↓)。梁支座A,B,D的反力为:FA=3kN(↓);FB=6kN(↑);FD=3kN(↑)。I图:解:求解顺序:先解CD部分再解ABC部分。解CD部分(1)取梁CD画受力图如上左图所示。(2)建直角坐标系,列平衡方程:∑Fy=0,FC-q×a+FD=0∑MC(F)=0,-q×a×0.5a+FD×a=0(3)求解未知量。将已知条件q=2kN/m,a=1m代入平衡方程。解得:FC=1kN;FD=1kN(↑)解ABC部分(1)取梁ABC画受力图如上右图所示。(2)建直角坐标系,列平衡方程:∑Fy=0,-F/C+FA+FB-F=0∑MA(F)=0,-F/C×2a+FB×a-F×a-M=0(3)求解未知量。将已知条件F=6kN,M=2kN·m,a=1m,F/C=FC=1kN代入平衡方程。解得:FB=10kN(↑);FA=-3kN(↓)梁支座A,B,D的反力为:FA=-3kN(↓);FB=10kN(↑);FD=1kN(↑)。J图:解:求解顺序:先解IJ部分,再解CD部分,最后解ABC部分。
解IJ部分(1)取IJ部分画受力图如右图所示。(2)建直角坐标系,列平衡方程:∑Fy=0,FI-50kN-10kN+FJ=0∑MI(F)=0,-50kN×1m-10kN×5m+FJ×2m=0(3)求解未知量。解得:FI=10kN;FJ=50kN解CD部分(1)取梁CD画受力图如图所示。(2)建直角坐标系,列平衡方程:∑Fy=0,FC-F/J+FD=0∑MC(F)=0,-F/J×1m+FD×8m=0(3)求解未知量。将已知条件F/J=FJ=50kN代入平衡方程。解得:FC=43.75kN;FD=6.25kN(↑)解ABC部分(1)取梁ABC画受力图如图所示。(2)建直角坐标系,列平衡方程:∑Fy=0,-F/C-F/I-FA+FB=0∑MA(F)=0,-F/C×8m+FB×4m-F/I×7m=0(3)求解未知量。将已知条件F/I=FI=10kN,F/C=FC=43.75kN代入平衡方程。解得:FB=105kN(↑);FA=51.25kN(↓)梁支座A,B,D的反力为:FA=51.25kN(↓);FB=105kN(↑);FD=6.25kN(↑)。K图:解:求解顺序:先解BC段,再解AB段。解BC段解AB段
(1)取梁BC画受力图如上左图所示。(2)建直角坐标系,列平衡方程:∑Fy=0,FC-q×a+FB=0∑MB(F)=0,-q×a×0.5a+FC×2a=0(3)求解未知量。将已知条件q=2kN/m,a=1m代入平衡方程。解得:FC=0.5kN(↑);FB=1.5kN(1)取梁AB画受力图如图所示。(2)建直角坐标系,列平衡方程:∑Fy=0,FA-q×a-F/B=0∑MA(F)=0,-q×a×1.5a+MA-F/B×2a=0(3)求解未知量。将已知条件q=2kN/m,M=2kN·m,a=1m,F/B=FB=1.5kN代入平衡方程,解得:FA=3.5kN(↑);MA=6kN·m(Q)。梁支座A,C的反力为:FA=3.5kN(↑);MA=6kN·m(Q);FC=0.5kN(↑)L图:解:求解顺序:先解AB部分,再解BC部分。解AB部分(1)取梁AB画受力图如图所示。(2)建直角坐标系,列平衡方程:∑Fy=0,FA-F+FB=0∑MA(F)=0,-F×a+FB×a=0(3)求解未知量。将已知条件F=6kN,a=1m代入平衡方程。解得:FA=0;FB=6kN解BC部分(1)取梁BC画受力图如图所示。(2)建直角坐标系,列平衡方程:∑Fy=0,FC-F/B=0∑MC(F)=0,F/B×2a+M-MC=0(3)求解未知量。将已知条件M=2kN·m,a=1m,F/B=FB=6kN代入平衡方程。解得:FC=6kN(↑);MC=14kN·m(P)。梁支座A,C的反力为:FA=0;MC=14kN·m(P);FC=6kN(↑)2.14试求A,B间的最小距离解(1)取水塔和支架画受力图如图所示。当AB间为最小距离时,处于临界平衡,FA=0。
(2)建直角坐标系,列平衡方程:∑MB(F)=0,-q×6m×21m+G×0.5lmin=0(3)求解未知量。将已知条件G=160kN,q=16kN/m代入平衡方程,解得:lmin=2.52m2.15试求汽车的最大起重量G解:(1)取汽车起重机画受力图如图所示。当汽车起吊最大重量G时,处于临界平衡,FNA=0。(2)建直角坐标系,列平衡方程:∑MB(F)=0,-G2×2.5m+Gmax×5.5m+G1×2m=0(3)求解未知量。将已知条件G1=26kN,G2=4.5kN代入平衡方程,解得:Gmax=7.41kN2.16试求汽车自重G2解:(1)分别取BCE和AOB画受力图如图所示。
(2)建直角坐标系,列平衡方程:对BCE列∑Fy=0,FBy-G2=0对AOB列∑MO(F)=0,-F/By×a+F×l=0(3)求解未知量。将已知条件FBy=F/By,F=G1代入平衡方程,解得:G2=lG1/a2.17求驱动力偶矩解:求解顺序:先解锯弓,再解锯床转盘。解锯弓(1)取梁锯弓画受力图如图所示。(2)建直角坐标系,列平衡方程:∑FX=0,F-FBAcos15º=0∑Fy=0,FD+FBAsin15º-FC=0∑MB(F)=0,-FC×0.1m+FD×0.25m+F×0.1m=0(3)求解未知量。将已知条件F=5kN代入平衡方程。解得:FBA=5.18kNFD=-2.44kN(↓)FC=-1.18kN(↑)解锯床转盘(1)取锯床转盘画受力图如图所示。 (2)建直角坐标系,列平衡方程:∑FX=0,FABcos15º-FOX=0∑Fy=0,FOy-FABsin15º=0∑MO(F)=0,-FABcos15º×0.1m+M=0(3)求解未知量。将已知条件FAB=FBA=5.18kN代入平衡方程,解得:FOX=5kN(→)FOy=1.34kN(↑)M=500N·m(Q)2.18求作用于曲柄OA上之力偶矩M解:
(1)分别取电机O,连杆AB,推料板O1C画受力图如图所示。(2)取连杆AB为研究对象∑MA(F)=0,-F/By×2m-G2×1m=0∑MB(F)=0,-FAy×2m+G2×1m=0∑Fx=0,FAx-F/Bx=0将已知条件G2=300N代入平衡方程,解得:FAy=150N;F/By=150N;FAx=F/Bx(3)取推料板O1C为研究对象∑MO1(F)=0,-FBx×0.4m×sinα+G×0.4m×cosα-FBy×0.4m×cosα+F×0.4m=0将已知条件G=600N,α=45°,F=1000N,F/By=FBy=-150N代入平衡方程,解得:FBx=2164NFAx=F/Bx=2164N(4)取电机O为研究对象∑MO(F)=0,-F/Ax×0.2m×cosα+F/Ay×0.2m×sinα+M=0将已知条件FAx=F/Ax=2164N,FAy=F/Ay=150N,α=45°代入平衡方程,解得:M=285N·m。2.19求人能够达到的最大高度 解:设能够达到的最大高度为h,此时梯子与地面间的摩擦力为最大静摩擦力。(1)取梯子画受力图如图所示。(2)建直角坐标系,列平衡方程:∑Fy=0,FNB-G-G人=0∑MA(F)=0,
-G×0.5l×cosα-G人×(l-h/sinα)×cosα-Ffm×l×sinα+FNB×l×cosα=0Ffm=fSFNB(3)求解未知量。将已知条件G=200N,l=3m,fS=0.25,G人=650N,α=60°代入平衡方程。解得:h=1.07mm2.20尺寸b应为多大解:由砖的受力图与平衡要求可知:Ffm=0.5G=0.5F;FNA=FNB至少要等于Ffm/fs=F=G再取AHB讨论,受力图如图所示:要保证砖夹住不滑掉,图中各力对B点逆时针的矩必须大于各力对B点顺时针的矩。即:F×0.04m+F/fm×0.1m≥F/NA×b代入Ffm=F/fm=0.5G=0.5F;FNA=F/NA=F=G可以解得:b≤0.09m=9cm2.21求制动所需的最小力F1的大小A图:解:(1)取圆轮、制动装置画受力图如图所示。(2)建直角坐标系,列平衡方程:取圆轮列平衡方程:∑MO(F)=0,-Ffm×r+M=0Ffm=fSFN解得Ffm=M/r;FN=M/rfS取制动装置列平衡方程:∑MA(F)=0,-F1×b-F/fm×c+F/N×a=0
解得:B图:解:(1)取圆轮、制动装置画受力图如图所示。(2)建直角坐标系,列平衡方程:取圆轮列平衡方程:∑MO(F)=0,-Ffm×r+M=0Ffm=fSFN解得Ffm=M/r;FN=M/rfS取制动装置列平衡方程:∑MA(F)=0,-F2×b+F/N×a=0解得:C图:解:(1)取圆轮、制动装置画受力图如图所示。(2)建直角坐标系,列平衡方程:取圆轮列平衡方程:∑MO(F)=0,-Ffm×r+M=0Ffm=fSFN解得Ffm=M/r;FN=M/rfS取制动装置列平衡方程:∑MA(F)=0,-F3×b+F/fm×c+F/N×a=0解得:
第四章轴向拉伸与压缩4.1求轴力画轴力图A图:解:(1)分段计算轴力杆件分为2段。用截面法取图示研究对象画受力图如图,列平衡方程分别求得:FN1=F(拉);FN2=-F(压)(2)画轴力图。根据所求轴力画出轴力图如图所示。B图:解:(1)分段计算轴力杆件分为3段。用截面法取图示研究对象画受力图如图,列平衡方程分别求得:FN1=F(拉);FN2=0;FN3=2F(拉)(2)画轴力图。根据所求轴力画出轴力图如图所示。
C图:解:(1)计算A端支座反力。由整体受力图建立平衡方程:∑Fx=0,2kN-4kN+6kN-FA=0FA=4kN(←)(2)分段计算轴力杆件分为3段。用截面法取图示研究对象画受力图如图,列平衡方程分别求得:FN1=-2kN(压);FN2=2kN(拉);FN3=-4kN(压)(3)画轴力图。根据所求轴力画出轴力图如图所示。D图:解:(1)分段计算轴力杆件分为3段。用截面法取图示研究对象画受力图如图,列平衡方程分别求得:FN1=-5kN(压);FN2=10kN(拉);FN3=-10kN(压)(2)画轴力图。根据所求轴力画出轴力图如图所示。
4.2求应力和应变解:4.3求杆件变形解:由截面法可以计算出AC,CB段轴力FNAC=-50kN(压),FNCB=30kN(拉)。4.4求应力和变形
4.5校核强度4.6校核强度
4.7设计直径4.8求所吊重物重量
4.9求许用荷载 4.10求弹性模量和泊松比
4.11求许用荷载4.12求支座反力第五章剪切与挤压的实用计算5.1计算切断力
5.2求螺栓直径与螺栓头高度的比例5.3计算焊接板的许用荷载
5.4求接头处所需的尺寸5.5求拉杆的许用荷载
第六章圆轴扭转6.1扭矩图A图:解:(1)计算扭矩。将轴分为2段,逐段计算扭矩。对AB段:∑MX=0,T1-3kN·m=0可得:T1=3kN·m对BC段:∑MX=0,T2-1kN·m=0可得:T2=1kN·m(2)画扭矩图。根据计算结果,按比例画出扭矩图如图。B图:
解:(1)计算扭矩。将轴分为3段,逐段计算扭矩。对AB段:∑Mx=0,T1+4.5kN·m-1.5kN·m-2kN·m=0可得:T1=-1kN·m对BC段:∑Mx=0,T2-1.5kN·m-2kN·m=0可得:T2=3.5kN·m对BC段:∑Mx=0,T3-2kN·m=0可得:T3=2kN·m(2)画扭矩图。根据计算结果,按比例画出扭矩图如图。6.2是否有利解:(1)计算外力偶矩。MA=9549×60/200=2864.7N·m同理可得:MB=954.9N·m,MC=716.2N·m,MD=1193.6N·m(2)计算扭矩。将将轴分为3段,逐段计算扭矩。对AB段:∑Mx=0,T1+MB=0可得:T1=-954.9N·m对BC段:∑Mx=0,T2+MB-MA=0可得:T2=1909.8N·m对BC段:∑Mx=0,T3-M=0可得:T3=1193.6N·m(3)画扭矩图。根据计算结果,按比例画出扭矩图如右图。(4)将轮A和轮C位置对调后,由扭矩图可知最大绝对值扭矩较之原来有所降低,对轴的受力有利。
6.3求圆轴传递功率解:WP=πd3/16=24543.7mm3由τmax=T/WP可得:T=1472.6N·m由M=T=9549×P/n可得:P=T×n/9549=18.5kW6.4空心与实心轴比较6.5校核轴强度和刚度
6.6设计轴直径
6.7求钢材的E和G第七章平面弯曲内力7.1指定截面上的剪力和弯矩A图 B图
C图D图
7.2画剪力图和弯矩图A图B图
C图
D图
E图
F图
7.3梁的剪力图和弯矩图解:(1)由静力平衡方程得:FA=F,MA=Fa,方向如图所示。(2)利用M,FS,q之间的关系分段作剪力图和弯矩图。(3)梁最大绝对值剪力在AB段内截面,大小为2F。梁最大绝对值弯矩在C截面,大小为2Fa。B图
解:(1)由静力平衡方程得:FA=3ql/8(↑),FB=ql/8(↑)。(2)利用M,FS,q之间的关系分段作剪力图和弯矩图。(3)梁的最大绝对值剪力在A右截面,大小为3ql/8。梁的最大弯矩绝对值在距A端3l/8处截面,大小为9ql2/128。C图解:(1)由静力平衡方程得:FB=2qa,MB=qa2,方向如图所示。(2)利用M,FS,q之间的关系分段作剪力图和弯矩图。(3)梁的最大绝对值剪力在B左截面,大小为2qa。梁的最大绝对值弯矩在距AC段内和B左截面,大小为qa2。D图
解:(1)由静力平衡方程得:FA=qa/2(↓),FB=qa/2(↓)。(2)利用M,FS,q之间的关系分段作剪力图和弯矩图。(3)梁的最大绝对值剪力在AC和DB段内,大小为qa/2。梁的最大弯矩绝对值在AB跨中间截面,大小为5qa2/8。E图
解:(1)由静力平衡方程得:FA=9qa/4(↑),FB=3qa/4(↑)。(2)利用M,FS,q之间的关系分段作剪力图和弯矩图。(3)梁最大绝对值剪力在A右截面,大小为5qa/4。梁最大弯矩绝对值在A截面,大小为qa2/2。F图解:(1)由静力平衡方程得:FA=F(↑),FB=3F(↑)。(2)利用M,FS,q之间的关系分段作剪力图和弯矩图。(3)梁最大绝对值剪力在DB段内截面,大小为3F。梁最大弯矩绝对值在D截面,大小为3Fa。
G图解:(1)由静力平衡方程得:FA=4.5qa(↑),FB=0.5qa(↑)。(2)利用M,FS,q之间的关系分段作剪力图和弯矩图。(3)梁最大绝对值剪力在A右截面,大小为3.5qa。梁最大弯矩绝对值在A右截面,大小为3qa2。 H图解:(1)由静力平衡方程得:FA=1.25qa(↑),FB=0.75qa(↑)。(2)利用M,FS,q之间的关系分段作剪力图和弯矩图。(3)梁最大绝对值剪力在CA段内截面,大小为qa。梁最大弯矩绝对值在A右截面,大小为qa2。
7.4试画梁的荷载图和弯矩图解:利用M,FS,q之间的关系推出荷载图和弯矩图如下。7.5判断图中的FS,M图是否有错A图解:有错,改正如下图。
B图解:有错,改正如下图。C图解:有错,改正如下图。
D图解:有错,改正如下图。第八章平面弯曲梁的强度与刚度计算
8.1立放和平放时产生的最大正应力8.2求梁内最大拉应力和最大压应力
8.3截面二次矩A图:B图:8.4截面二次矩
8.5选择此梁的工字钢型号
8.6求内经d的最大值8.7试校核此梁的强度
8.8设计正方形截面和矩形截面
8.9求最大许可荷载[F]8.10试校核压板的强度
8.11点和b点的正应力和切应力
8.12求梁内最大正应力和切应力8.13试校核梁的强度
8.14试选择合适的工字钢型号
第九章应力状态与强度理论9.1求试样拉力F9.2求最大正应力和最大切应力9.3绘出A点处的原始单元体A图解:
B图解:9.4求图示单元体指定斜面上的应力A图:B图:
C图:9.5求主应力的大小和主平面的方位A图:
B图:C图:
9.6求主应力的大小和主平面的方位A图:B图
9.7试对钢制零件进行强度校核1)2)
9.8试对铸铁零件进行强度校核1)2)9.9按第三强度理论设计壁厚δ9.10第三和四强度理论校核轴的强度
第十章组合变形时杆件的强度计算10.1试求切口的允许深度10.2试校核梁的强度
10.3最大压应力之比10.4确定许用荷载[F]
10.5选择圆柱的内径d
10.6按第三强度理论校核轴的强度
10.7按第三强度理论校核轴的强度
'
您可能关注的文档
- 工程力学习题解答.doc
- 工程力学习题集及部分解答指导.doc
- 工程力学作业解答(重大版).doc
- 单辉祖_谢传锋_著)_高等教育出版社_课后答案.doc
- 工程力学答案.doc
- 工程力学答案.pdf
- 工程力学课后习题答案.doc
- 工程力学课后习题答案.pdf
- 工程力学课后答案 高等教育出版社出版.doc
- 工程力学课后答案-高等教育出版社出版.doc
- 工程力学课后答案.doc
- 工程力学课后答案.pdf
- 工程力学课后答案合_单祖辉主编.doc
- 工程化学(魏云鹤)习题解答.pdf
- 工程数学《复变函数》西安交通大学第四版高等教育出版社课后习题答案.doc
- 工程数学习题答案.doc
- 工程数学习题集(含部分湖大版《大学数学5》课后答案).doc
- 工程材料与成型工艺基础习题汇编答案--老师版.doc