- 1.30 MB
- 2022-04-29 13:52:40 发布
- 1、本文档共5页,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,可选择认领,认领后既往收益都归您。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细先通过免费阅读内容等途径辨别内容交易风险。如存在严重挂羊头卖狗肉之情形,可联系本站下载客服投诉处理。
- 文档侵权举报电话:19940600175。
'平新乔《微观经济学十八讲》答案目录第一讲偏好、效用与消费者的基本问题.....................................................................................2第二讲间接效用函数与支出函数.................................................................................................9第三讲价格变化对消费者配置效应与福利效应.......................................................................18第四讲VNM效用函数与风险升水............................................................................................25第五讲风险规避、风险投资和跨期决策...................................................................................32第六讲生产函数与规模报酬.......................................................................................................45第七讲要素需求函数、成本函数、利润函数与供给函数.......................................................57第八讲完全竞争与垄断...............................................................................................................68第九讲Cournot均衡、Bertrand均衡与不完全竞争..................................................................80第十讲策略性博弈与纳什均衡...................................................................................................93第十一讲广延型博弈与反向归纳策略.....................................................................................100第十二讲子博弈与完美性.........................................................................................................105第十三讲委托–代理理论初步.................................................................................................110第十四讲信息不对称、逆向选择与信号博弈.........................................................................118第十五讲工资、寻找工作与劳动市场中的匹配.....................................................................125第十六讲一般均衡与福利经济学的两个基本定理.................................................................134第十七讲外在性、科斯定理与公共品理论.............................................................................140
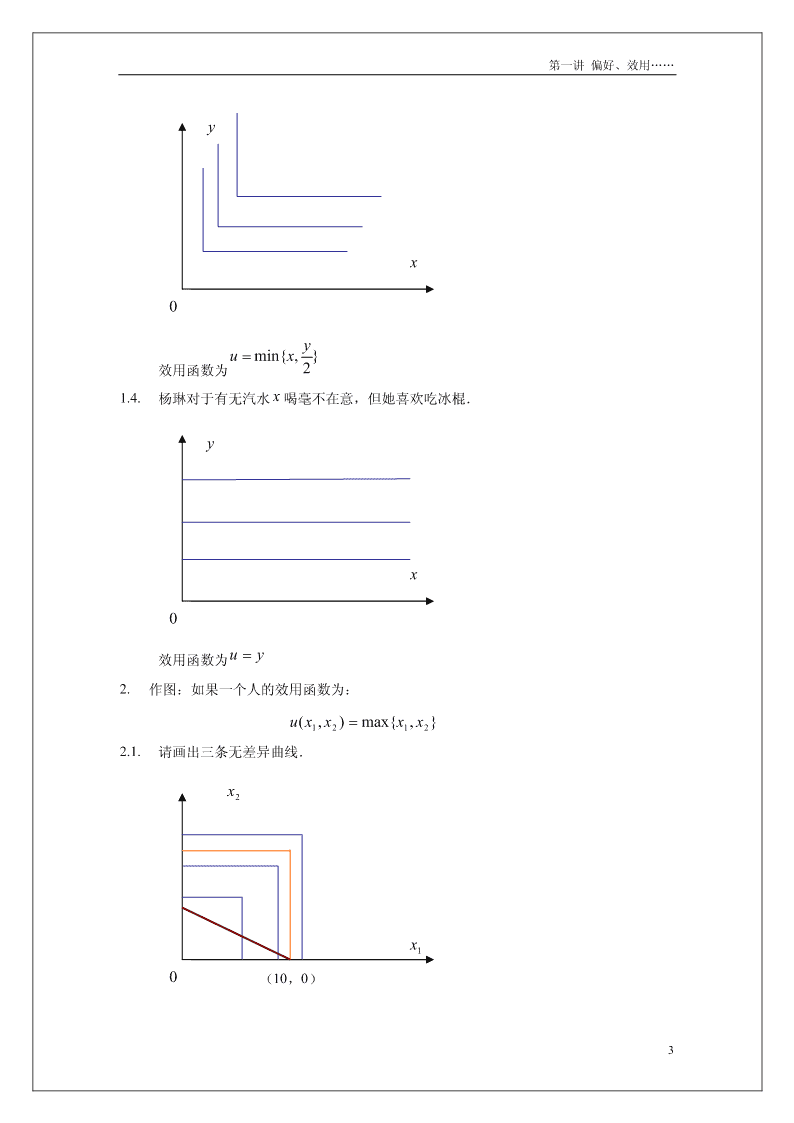
第一讲偏好、效用……第一讲偏好、效用与消费者的基本问题1.根据下面的描述,画出消费者地无差异曲线.对于1.2和1.3题,些出效用函数.1.1.王力喜欢喝汽水x,但是厌恶吃冰棍y可能的一个无差异曲线是这样:yx01.2.李楠既喜欢喝汽水x,又喜欢吃冰棍y,但她认为三杯汽水和两根冰棍是无差异的.只要满足(0,2)和(3,0)在同一条无差异曲线上就符合题目要求.可能的一个无差异曲线是这样:y2x031.3.萧峰有个习惯,它每喝一杯汽水x就要吃两根冰棍,当然汽水和冰棍对他而言是多多益善.2
第一讲偏好、效用……yyx0yu=min{x,}效用函数为21.4.杨琳对于有无汽水x喝毫不在意,但她喜欢吃冰棍.yx0效用函数为u=y2.作图:如果一个人的效用函数为:u(x1,x2)=max{x1,x2}2.1.请画出三条无差异曲线.x2x10(10,0)3
第一讲偏好、效用……2.2.如果p1=1,p2=2,y=10.请在图上找出该消费者的最优的消费组合.在图中,赭线是预算线.与之有公共点集的唯一最高无差异曲线是过点(10,0)的那条无差异曲线(上图中为橙线).消费者的最优的消费选择是(10,0).3.下列说法对吗?为什么?若某个消费者的偏好可以由效用函数22uxx=x+xx+x−(1,2)10(12122)50来描述,那么对此消费者而言,商品1和商品2是完全替代的.答:此说法正确.u+50t(x,x)=12令10,由单调变换的定义知,t与u是同一个偏好的效用函数.且t(x,x)=x+x,即t所描述的偏好中,商品1与商品2是完全替代的.因此u所描1212述的偏好中,商品1与商品2是完全替代的.4.若某个消费者的效用函数为11u(x,x)=lnx+lnx121222其中,x1,x2∈R+4.1.证明:x1与x2的边际效用都递减.证明:u(x1,x2)对x1取二阶偏导:2∂u1=−<022∂x2x11i因此x1的边际效用是递减的.同理,x2的边际效用也是递减的.4.2.请给出一个效用函数形式,使该形式不具备边际效用递减的性质.答:可能的一个效用函数是u(x1,x2)=x1+x2.5.常见的常替代弹性效用函数形式为1(ρρ)u(x,x)=αx+αxρ121122请证明:5.1.当ρ=1,该效用函数为线性.证明:当ρ=1时,效用函数为u(x1,x2)=α1x1+α2x2此时,函数u是线性的.4
第一讲偏好、效用……u(x,x)=xα1xα25.2.当ρ→0时,该效用函数趋近于1212α1β=1α+α证明:令12,β2=1−β1.则u的一个单调变换结果是1ρρρt=(βx+βx)1122又:1(ρρ)lnβ1x1+β2x2ρlimt(x,x)=lime12ρ→0ρ→0ρρlim1⎛βxρ+βxρ⎞limβ1x1lnx1+β2x2lnx21ββρρln⎜⎝1122⎟⎠ρ→0ρρlnx11x22→0β1x1+β2x2β+βββ=e=e=e12=x1x212t(x,x)=xβ1xβ2u(x,x)=xα1xα21212的一个单调变换结果是1212,因此,当ρ→0时,原效用函数所描述的偏好趋近于效用函数u(x,x)=xα1xα21212所描述的偏好.如果α1与α2满足α1+α2=1,那么当ρ→0时,同时有效用函数1(ρρ)u(x,x)=αx+αxρ121122趋近于以下效用函数:u(x,x)=xα1xα21212ii5.3.当ρ→−∞时,该效用函数趋近于u(x1,x2)=min{x1,x2}α1β=1α+α证明:令12,β2=1−β1.则u的一个单调变换结果是1ρρρt=(βx+βx)1122当x1x2时,有limt(x,x)=x122ρ→−∞5
第一讲偏好、效用……当x1=x2时,有t(x1,x2)≡x1=x2综上所述,当ρ→−∞时,原效用函数描述的偏好关系趋近于u(x1,x2)=min{x1,x2}所描述的偏好关系.如果α1与α2满足α1+α2=1,那么当ρ→−∞时,同时有效用函数1(ρρ)u(x,x)=αx+αxρ121122趋近于以下效用函数:u(x,x)=min{x,x}12126.茜茜总喜欢在每一杯咖啡里加两汤匙糖.如果每汤匙糖的价格是p1,每杯咖啡的价格是p2,她有M元可以花在咖啡和糖上,那么她将打算购买多少咖啡和糖?如果价格变′′为p1和p2,对她关于咖啡和糖的消费会发生什么影响?解:咖啡和糖对茜茜而言是完全互补品(perfectcomplements),即她的效用函数可以表示为(假设她的偏好满足单调性):1u(c,s)=min{c,s}2其中,c代表咖啡的量,以杯为单位;s表示糖的量,以汤匙为单位.很明显,她的最优选择必然是1c=s2(*)1c≠s考虑2,那么“多”出来的糖或者咖啡不会让茜茜觉得更好,反而还浪费了——1c=s还不如将买“多”出来的糖或咖啡的钱用来买咖啡或糖使得2.她面临的约束条件为:p1c+p2s≤M由于她的偏好是单调的,而收入的增加可以有机会买到更多量的咖啡和(或)糖,因此她的最优选择必然在预算线上.也就是说,她的约束条件可以表达为:p1c+p2s=M(**)2MMs=c=p+2pp+2p综合*与**式,可以得到,12,126
第一讲偏好、效用……2MMs′=c′=′′p′+2p′p′+2p′如果价格变成p1和p2,同样可以得到12,12.咖啡和糖的消费比例不会发生变化.7.令≥为偏好关系,>为严格偏好关系,≈为无差异关系.证明下列关系7.1.≥⊂≥说明:感觉能力不济;这道题只能说说自己的想法了.由于偏好的完备性,因此定义在任何一个选择集上的偏好关系都是唯一的.又由于任何集合都是自己的子集,所以≥⊂≥7.2.=⊂≥证明:≈=≥∩≤⇒≈⊂≥7.3.≈∪>=≥证明:≈=≥∩≤⎫⎬>=≥−≤⎭⇒≈∪>=≥7.4.≈∩>=∅证明:≈=≥∩≤⎫⎬>=≥−≤⎭⇒≈∪>=≥8.证明下列结论(或用具说服力的说理证明)8.1.>与≈都不具有完备性说明:严格偏好关系真包含于偏好关系,而偏好关系是完备的,因此,严格偏好关系不具有完备性.同理可以说明无差异关系也不具有完备性.8.2.≈满足反身性说明:如果无差异关系不具有完备性,那么根据无差异关系的定义,则必存在一个消费束严格偏好于它自身,也就是说,这个消费束同时既偏好于它本身又不偏好于它本身,这是矛盾的.8.3.严格偏好关系不满足反身性说明:如果严格偏好关系满足反身性,那么根据严格偏好关系的定义,则对任一对消费束a,b,如果a严格偏好于b,则说明b不可能偏好于a;而根据假设b严格偏好于a,b必然偏好于a.因此它们是矛盾的.121221128.4.对于任何X中的x与x,在下列关系中,只能居其一:x>x,x>x,或x≈x122112说明:根据8.3的说明,x>x与x>x不可能同时成立,那么,当x>x和21122112x>x同时不成立的时候,必有x≥x且x≥x,即x≈x9.一个只消费两类物品的消费者面临正的价格,其拥有正的收入,他的效用函数为:u(x1,x2)=x1导出其马歇尔需求函数.7
第一讲偏好、效用……解:解线性规划maxu(x,x)12x1,x2s.t.px+px=y1122由约束条件p1x1+p2x2=y知y−px22x=1p1yypp当x2=0时,u有最大值1.此时,x1的消费量为1.yp即,马歇尔需求函数为x1=1,x2=0α1−αu(x,x)=Axx,这里0<α<1,A>0.假定存在内点解,10.一个人的效用函数为1212请导出其马歇尔效用函数.解:解线性规划α1−αmaxAxx12x1,x2..+=stp1x1p2x2y其拉格朗日函数为α1−αLλxx=Axx+λy−px−px(;1,2)12(1122)使L(⋅)最大化的x1,x2,λ满足一阶条件:∂Lα−11−α=αAxx−λp=0121∂x1(1)∂Lα−α=(1−α)Axx−λp=0122∂x2(2)∂L=y−xp−xp=01122∂λ(3)将1式除以2式,得αx2p1x1p11−α=x=21−αxppα12,即2(4)代4式入3式,得αyx=1p1(5)8
第一讲偏好、效用……代5式入4式,得(1−α)yx=2p2(6)5与6式即为x1与x2的马歇尔需求函数.第二讲间接效用函数与支出函数u=alnq+q1.设一个消费者的直接效用函数为12.构造出该消费者的间接效用函数.并且运用罗尔恒等式去构造其关于两种物品的需求函数.验证:这样得到的需求函数与从直接效用函数推得的需求函数是相同的.解:解线性规划:max(alnq+q)12q1,q2s.t.pq+pq=y1122y−pq11q=2p将约束条件变形为2,将它代入式alnq1+q2中,我们的问题转化为:y−pq11max(alnq+)1q1,q2p2满足最大化的一阶条件是:1pap12a−=0⇒q=1qpp121代入约束条件中,可以得到:y−ap2q=2p2即为消费者的需求函数.消费者的间接效用函数为:apy−ap22v(p,y)=aln+pp12由罗尔恒等式,有:9
第二讲间接效用……p⎛ap⎞1⎜2⎟∂va−⎜2⎟∂p1ap2⎝p1⎠ap2q=−=−=1∂v1p1∂yp2p1ay∂va−2∂papppy−ap22122q=−=−=2∂v1p2∂yp2与从直接效用函数中推得的结果一致.2u(x,x)=xx,商品1和2的价格分别是p和p,此消费2.某个消费者的效用函数是121212者的收入为m,求马歇尔效用函数和支出函数.解:解线性规划:2maxxx12x1,x2..+=stp1x1p2x2y其拉格朗日函数为:2Lλxx=xx+λy−px−px(;1,2)12(1122)使L(⋅)最大化要求x1,x2,λ满足一阶条件∂L=2xx−λp=0121∂x11∂L2=x−λp=012∂x22∂L=y−px−px=01122∂λ31式除以2式,得:2xppx2111=⇒x=2xp2p1224代4入3式,得x1的需求函数:32yy−px=0⇒x=11123p15代5入4式,得x2的需求函数:10
第二讲间接效用……yx=23p26代5、6两式入效用函数中,得到当效用最大化时有间接效用函数:22⎛2y⎞yv(p,y)=u(x,x)=xx=⎜⎟1212⎜⎟3p3p⎝1⎠2又消费者效用最大化意味着y=e()p,v(p,y)即可得到支出函数:11232e()p,u=e(p,v(p,y))=y=()108ppu3=()2ppu3121223.考虑下列间接效用函数mv()p,p,m=12p+p12这里m表示收入,问:**xppm与x(p,p,m)什么是该效用函数所对应的马歇尔需求函数1(1,2,)212iii解:根据罗尔恒等式,可以得到这个效用函数所对应的马歇尔需求函数:m∂v−()2∂p1p1+p2mx=−=−=1∂v1p+p12∂yp+p12m∂v−()2∂p1p1+p2mx=−=−=2∂v1p+p12∂yp+p124.考虑一退休老人,他有一份固定收入,想在北京、上海与广州三成事中选择居住地.假定他的选择决策只根据其效用函数,设该效用函数的形式为u=x1x2,这里()2aabbx,x∈R.已知北京的物价为(p,p),上海的物价为(p,p),并且12+1212aabbababpp=pp,但p≠p,p≠p.又知广州的物价为12121122cc⎛1ab1ab⎞()p1,p2=⎜()p1+p1,()p2+p2⎟⎝22⎠.若该退休老人是理智的,他会选择哪个城市去iv生活?abc解:设老人在北京、上海、广州的效用分别为u,u,u,设老人的收入为m.11
第二讲间接效用……有22mm+abaabb22⎡⎤u+uc4p1p24p1p2mm112−u=−cc=⎢aa+bb−cc⎥224pp8pppppp12⎣121212⎦aabbpp=pp,所以因为1212ab2u+ucm⎡11⎤−u=⎢aa−cc⎥24pppp⎣1212⎦(*)ababp≠p,p≠p,有又11222821=<=pcpc()pa+pb()pa+pbpapapbpbpapa121122121212(**)abu+uc−u<0由*与**,得2abacbc又u=u,所以有u−u<0,u−u<01即老人将选择在广州生活.5.()2x,x∈R,求与该效用函数想对应的支出函数e()p,p,u5.1.设u=x1x2,这里12+12.解:解线性规划:minpx+px1122x1,x2s.t.xx=u12其拉格朗日函数为:L()λ;x,x=px+px+λ(.u−xx)12112212使L(⋅)最大化要求x1,x2,λ满足一阶条件∂L=p−λx=012∂x11∂L=p−λx=021∂x22∂L=u−xx=012∂λ31该题解答的修正得益于网友caidb在中心论坛上的帖子.关于caidb的个人信息在http://forum.ccer.edu.cn/forum/user_info.asp?id=121264上12
第二讲间接效用……e()p,p,u由1式、2式,得12pp12x=x=21λ,λ4代4入3,得pppp1212u−=0⇒λ=2λu5代5入4,得upup12x=x=21pp2,1于是可以得到对应的支出函数e()p,p,u=px+px=2ppu121122122′(x,x)∈R,求与该效用函数想对应的支出函数5.2.又设u=lnx1+lnx2,同样12+e′()p,p,u′12解:解法与5.1完全相同,得到()u′e′p,p,u′=2ppe1212e′()p,p,u′=e()p,p,u5.3.证明:1212u=x1x2⎫u′lnu⎬⇒u′=lnu⇒2p1p2e=2p1p2e=2p1p2uu′=lnx+lnx证明:12⎭根据5.1与5.2的结果,得到e′()p,p,u′=e(p,p,u)1212mv()p,p,m=12α1−αpp6.设某消费者的间接效用函数为12,这里0<α<1.什么是该消费者对物品1的希克斯需求函数?解:若消费束x是消费者的最优选择,那么根据引理一,间接效用函数与支出函数存在以下关系m=e()p,v(p,m)1由该消费者的间接效用函数,得到α1−αm=upp,其中u=v(p,p,m)21212由1式和2式,得到()()α1−αep,vp,m=upp1213
第二讲间接效用……因此,由Shepard引理,得到α−1αh∂e⎛p1⎞h∂e⎛p1⎞x==u⎜⎟x==u⎜⎟1∂p⎜p⎟2∂p⎜p⎟1⎝2⎠,2⎝2⎠7.考虑含n种商品的Cobb-Douglass效用函数nu(x)=A∏xαiii=1n∑αi=1这里,A>0,i=17.1.求马歇尔需求函数解:解线性规划:nmaxA∏xαiixi=1s.t.px=y其拉格朗日函数为:nL()λ;x=A∏xαi+λ(y−px)ii=1使L(⋅)最大化要求x1,x2,λ满足一阶条件∂Lα−1αu=αxjA∏xi−λp=α−λp=0jjijjj∂xji≠jxj,j=1,2,3,...,n1∂L=y−px=0∂λ2由1式,得uαjx=jλpj,j=1,2,3,...,n3代3入2,得nnu∑αiuαii=1uuy−∑pi=y−=y−=0⇒λ=i=1λpiλλy4代4入3,得希克斯需求函数αyjx=jpj,j=1,2,3,...,n14
第二讲间接效用……7.2.求间接效用函数解:根据7.1的结果nnαinαinαi⎛αy⎞∑αi⎛α⎞⎛α⎞v()p,y=u(x)=A∏⎜i⎟=Ayi=1∏⎜i⎟=Ay∏⎜i⎟⎜⎟⎜⎟⎜⎟i=1⎝pi⎠i=1⎝pi⎠i=1⎝pi⎠其中x为消费者的需求量.7.3.计算支出函数(同第6题的解法.不过这样的写法可能会好些☺)解:令αin⎛⎞α⎜i⎟u=v(p,y)=Ay∏⎜⎟i=1⎝pi⎠得到−αin⎛⎞−1αiy=uA∏⎜⎜⎟⎟i=1⎝pi⎠又由y=e(p,v()p,y),得到αin⎛⎞−1pie()p,u=uA∏⎜⎜⎟⎟i=1⎝αi⎠7.4.计算希克斯需求函数解:根据Shepard引理和7.3的结果,得到希克斯需求函数αih∂e−1αj−1⎛αi⎞xj==uApj∏⎜⎜⎟⎟∂pji≠j⎝pi⎠,j=1,2,3,...,n8.以Cobb-Douglass效用函数为例说明求解效用最大化问题和求解支出最小化问题可以得到同一需求函数.nu(x)=A∏xαii解:令效用函数形式为i=1,预算约束为px=y*************************************************************求解效用最大化问题得到的需求函数为(见7.1题)αyjx=jpjj=1,2,3,...,n,*************************************************************求解支出最小化问题的拉格朗日函数为n⎛α⎞L′()λ;x=px+λ′⎜u−A∏xi⎟⎜i⎟⎝i=1⎠L(⋅)x,λ′使最大化要求满足一阶条件15
第二讲间接效用……λ′uαjx=jpj1nαiu−A∏xi=0代入i=1,得αiαin⎛⎞n⎛⎞αi−1piu−Aλ′u∏⎜⎜⎟⎟=0⇒λ′=A∏⎜⎜⎟⎟i=1⎝pi⎠i=1⎝αi⎠2代2入1得到希克斯需求函数:αiλ′uαn⎛p⎞αhj−1⎜i⎟jxj==A∏⎜⎟upji=1⎝αi⎠pj,j=1,2,3,...,n3nu(x)=A∏xαii代i=1入3得到αin⎛p⎞αh⎜i⎟jxj=∏⎜xi⎟i=1⎝αi⎠pj,j=1,2,3,...,n4px=y代4入预算约束得nαinαinαin⎡⎛p⎞αj⎤⎡⎛p⎞⎤⎛n⎞⎡⎛p⎞⎤ii⎜⎟iy=∑pj⎢∏⎜⎜xi⎟⎟⎥=⎢∏⎜⎜xi⎟⎟⎥⎜∑αj⎟=⎢∏⎜⎜xi⎟⎟⎥j=1⎢⎣i=1⎝αi⎠pj⎥⎦⎢⎣i=1⎝αi⎠⎥⎦⎝j=1⎠⎢⎣i=1⎝αi⎠⎥⎦5代5入4得αin⎛p⎞αyαh⎜i⎟jjxj=∏⎜xi⎟=i=1⎝αi⎠pjpj,j=1,2,3,...,n6由3式与6式知,求解支出最小化与效用最大化得到的需求函数是一样的.9.下列说法对吗?为什么?1xh(p,u)=(p+u)2函数jxx可以作为某种商品的希克斯需求函数.答:不对.由于该需求函数仅与该商品的价格相关,因此可以令所有其它商品的消费量为零.根据Shepard引理,支出函数是该希克斯需求函数的一个原函数.又123()p+u2dp=()p+u2+C∫xxx323()p+u2+Cxp其中,无论C取什么值,3都不是x的一次齐次函数,因此该函数不可以作为某种商品的希克斯需求函数.10.下列函数能成为一个马歇尔需求函数吗?为什么?2pI()xxp,p,y=xy22p+pxy16
第二讲间接效用……这里,x与y是两种商品,I为收入.答:假设该函数是一个马歇尔需求函数.∂x>0由∂I可知,x是正常商品,它的需求量在任何情况下随收入上升而上升.∂x>0又当py>px时,∂px,因此在py>px时,x的需求量随价格上升而上升.p>p综上所述,当yx时,该商品的替代效应为正.而任何商品价格变化对该商品需求量所起的替代效应为非正.因此,该函数不是一个马歇尔需求函数.17
第三讲价格变化……第三讲价格变化对消费者配置效应与福利效应1.证明,x1与x2不可能都是劣等品.说明:如果仅仅要求偏好满足完备性与传递性假设,两个产品都是劣等品是可能的.如果要求偏好满足局部非餍足性,那么一个产品都成不了劣等品.也就是说,这是不可能的.如果再加些性状良好(单调性、凸性或严格凸性)的条件,这就更不可能了.2.如果偏好是凹的,替代效应仍然为负吗?答:不是.对不同相对价格水平来说,替代效应为零或负无穷大.3.已知一个消费者对牛奶的需求函数为yx=10+10p这里x为一周内牛奶的消费量,y=120元为收入,p=3元/桶,现在假定牛奶价格从p′3元降为=2元.问:3.1.该价格变化对该消费者的需求总效应是多少?(即其牛奶消费会变化多少?)yyx=10+=14x′=10+=16解:10p,10p′.所以需求的变化量∆x=x′−x=2桶3.2.请算出价格变化的替代效应.这里的替代效应指斯勒茨基替代效应.有:y′′=y+∆px=120+(−1)×14=106y′′x′′=10+=15.310p′s因此,价格变化的替代效应∆x=x′′−x=1.33.3.请算出价格变化的收入效应.m解由3.1与3.2得,价格效应为∆x=x′−x′′=0.72u(x,x)=xxpp4.某个消费者的效用函数为1212.令1,2与m分别表示商品1的价格、商品2的价格和收入.18
第三讲价格变化……4.1.如果m=24,p1=1,p2=1,现在p1上升为2,求此消费者关于商品1的斯拉茨基替代效应和收入效应.′解:令x1为商品1价格变化前的消费量,x1为变化后的消费量.有:2m′2mx==8x==161′13p3p1,1′′令x1为调整收入以保持购买力条件下,对商品1的消费量.m′′为为保持购买力对收入进行调整后得到的收入.有:m′′=m+p′px(−)1=24+(2−1)×16=402m′′2×4040x′′===13p′3×23s其中,斯拉茨基替代效应∆x为408x′′−x=−16=−1133m收入效应∆x为4016x′−x′′=8−=−11334.2.请根据计算,验证恩格尔加总规则.解:由4.1知2∂x1y224∂x2y124S=S=1η1=×=×=1η1=×=×=112∂yx1316∂yx383,3,,2因此S1η1+S2η2=1恩格尔加总规则成立.5.(单项选择)当价格是(3,1)时,某个消费者选择的消费束是(x,y)=(6,6).在新(p,p)的价格xy下,他选择的消费束是(x,y)=(5,8),若此消费者的行为满足显示偏好的弱公里,那么必定有:2p3p3p=p(1)yx(2)xy(3)xy(4)xy解:选择1.如果该消费者的行为满足显示偏好弱公理,那么必然有6p+6p>5p+8pxyxy即:19
第三讲价格变化……2p0.7.1.求反需求函数p(Q)1−ε⎛A⎞εQ=Ap⇒p=⎜⎜⎟⎟解:⎝Q⎠7.2.计算需求的价格弹性∂Qp−ε−1pE=×=−ε×Ap×=−ε=ε−ε∂pQAp解:7.3.ε的值为多少时,称需求是无弹性的?答:当ε<1时,称需求是无弹性的.p(Q)7.4.证明边际收入函数对反需求函数的比,MR(Q),独立于产出Q.111−TR(Q)=pQ=AεQε,因此证明:1dTR⎛1⎞⎛A⎞εMR(Q)==⎜1−⎟⎜⎜⎟⎟dQ⎝ε⎠⎝Q⎠p(Q)1εMR(Q)==p(Q)1−1ε−1因此,ε,因此MR(Q)与Q无关.8.判断下述论断是否正确,并给出理由:8.1.如果需求曲线是一条直线,则直线上各点的需求价格弹性是一样的.判断:并不是所有直线上的弹性都是一样的.20
第三讲价格变化……理由:一类线性需求曲线可以由q=−ap+b,a>0,b>0来表示,它的弹性dqpapE==dpq−ap+b即,弹性E是价格p的函数,也就是说,这样的直线上需求价格弹性是随价格变化,不是一样的.但考虑与x轴垂直的需求曲线(a=0),它的弹性就是不变的.最后考虑与x轴水平的需求曲线,它的弹性不存在(无穷大的),讨论各点上的弹性是否相等无意义.8.2.如果对X的需求是由X的价格、Y的价格和收入决定的,则当X的价格、Y的价格和收入都上涨一倍时,对X的需求不变.判断:正确理由:考虑典型的预算约束表达式pxx+pyy≤m,其中px、py和m分别为X、Y的价格和收入.在这样的预算约束和一定的偏好下,消费者将选择一定的X和Y的消费量.消费者的选择变化无非基于两个条件的变化,这两个条件就是选择集-预算约束和偏好.当X的价格、Y的价格和收入都上涨一倍时,其预算约束为()2px+(2p)y≤2mpx+py≤mxy,它与xy表示的是同样的选择集,在偏好不变的情况下(这是“如果对X的需求是由X的价格、Y的价格和收入决定的”的含义),消费者的选择将不会发生变化,也就是说,对X的需求不变.9.判断对错并简要说明理由:∂x1>0x1和x2是一个消费者消费的两种物品,我们说x1是x2的替代品,如果∂p2,p2为x2的价格.如果x1是x2的替代品,则x2也是x1的替代品.判断:第一句错误,第二句正确.说明:两个商品之间的替代关系是通过净替代效应的正负来定义的(张定胜《高级微观经济学》第一章),也即是对x1的希克斯需求函数求p2的偏导,如果是正,则替代,是负为互补.根据马歇尔需求函数求偏导得出的是总替代和总互补关系,即使总替代关系为正,由于未剔除收入效应,仍有可能净替代效应为负,从而两种商品互补.该命题第一句是错误的.根据净替代效应的对称性,如果商品2是商品1的替代品,则1也是2的替代品,命题21
第三讲价格变化……2第二句是正确的.10.以需求函数q=a−bp为例,试分析为什么在需求曲线缺乏弹性的部分经营不可能产生最大利润.分析:该需求的弹性表达式为dqppbpE==−b=dpqa−bpa−bp需求曲线缺乏弹性时,有bpa<1⇒p0,()≥0企业的利润函数为π=TR−C最大利润产生在利润对价格一阶导等于零的地方:dπdTRdCdqa+bc′(q)a=−=a−2bp+bc′(q)=0⇒p=>dpdpdqdp2p2b因此在需求曲线缺乏经营不可能产生最大利润.11.判断对错并简要说明理由:11.1.如果消费者是一个理性的效用最大化者,那么他对某种商品的斯拉茨基替代效应必定是负的.错.考虑完全互补偏好,相对价格变化的斯拉茨基替代效应为零.αβ11.2.假设某消费者的效用函数是u(x,y)=xy,则他关于x的需求对y价格的交叉价格弹性为零.αmx=对.他关于x的需求为()α+βpx,其中m为收入,px为x的价格.从需求函∂x=0∂xpyE==0p∂pxy数与y的价格y无关可以得到y,由此可以得到∂pyx.12.下面的说法对吗?为什么?某个消费者将他的全部收入花在两种商品上,其中一种商品是吉芬商品.如果吉芬商品的价格上升,那么他对另外一种商品的需求必定下降.对.如果吉芬商品价格上升,消费量增大,另一种商品的预算份额下降,在价格不变的前提下,需求必定下降.2该题解答的修正得益于网友54gg在中心论坛上的回复.关于54gg的个人信息请见http://forum.ccer.edu.cn/forum/user_info.asp?id=14260322
第三讲价格变化……⎛h⎞∂x⎜i⎟⎜⎝∂pj⎟⎠sijsijxxj13.令斯拉茨基公式中右端第一项为,叫做i与的净替代效应.对于效用r=,证明:sp+sp=0函数ux1x2111122r=和预算约束px≤y,得到x、x的需求函数证明:由ux1x212ryyx=x=12(1+r)p(1+r)p1,2由此可以得到间接效用函数r1+rryv(p,y)=r+1r(1+r)pp12然后,根据本章引理一,得到1⎛prpu⎞1+r⎜12⎟e(p,u)=(1+r)⎜r⎟⎝r⎠s由Shepherd引理和ij的定义,得到112⎡2+r1⎤11∂e(p,u)r⎛u⎞1+r−r⎛u⎞1+r−ps=p=p⎢−⎜⎟p1+rp1+r⎥=−⎜⎟p1+rp1+r111121⎢r12⎥r12∂p11+r⎝r⎠1+r⎝r⎠⎣⎦112⎡1r⎤11∂e(p,u)r⎛u⎞1+r−−r⎛u⎞1+r−ps=p=p⎢⎜⎟p1+rp1+r⎥=⎜⎟p1+rp1+r21222⎢r12⎥r12∂p1∂p21+r⎝r⎠1+r⎝r⎠⎣⎦因此,s11p1+s12p2=014.我们观察到,一个消费者在p1=2,p2=6时,购买的x1=20,x2=10;当价格为p=3,p=5时,购买的x=18,x=4.他的行为符合显示性偏好的弱公理吗?1212答:符合.如果要符合显示性偏好弱公理,因为2×20+6×10=100≥2×18+6×4=60所以必然应当预测到3×20+5×10≥3×18+5×4而后一个等式确实是成立的(110≥74),符合预测.因此他的行为符合显示性偏好的弱公理.15.设消费者的反需求函数为p=a−bq,这里a,b>0.假定政府开征消费税(从价税),因此消费者支付的价格会从p上升到p(1+t)(这里,t为税率).证明:消费者剩余的23
第三讲价格变化……损失总是超过政府通过征税而获得的收入.证明:征税前消费者的消费者剩余为1()1()⎛a1⎞CS=a−pq=a−p⎜−p⎟22⎝bb⎠征税后,消费者的剩余为1[]()⎡a1()⎤CS′=a−p1+t−p1+t⎢⎥2⎣bb⎦他们所损失的消费者剩余为2221⎛apta2ptpt⎞∆CS=CS′−CS=⎜−−pt++⎟⎜⎟2⎝bbbb⎠政府征税所获收入为⎡a1()⎤T=pt−p1+t⎢⎥⎣bb⎦221⎛pt⎞T+∆CS=⎜−⎟<0⎜⎟因此,2⎝b⎠即消费者剩余的损失总是超过政府通过征税而获得的收入.16.设一个消费者只消费两类商品,他在p1=10元,p2=5元时购买了x1=5,x=10.现在,p下降至8元,p上升至6元.问该消费者的生活水平在价格变动212后提高了还是降低了?为什么?答:因为价格变化前后,消费者都能买到x1=5和x2=10(购买力不变),也就是说,他至少会和价格变化前一样好.在不清楚消费者的偏好是否连续和可导的情况下,还不能判定他的效用水平(也就是生活水平)会不会有提高.24
第四讲VNM效用……第四讲VNM效用函数与风险升水−bw1.(单项选择)一个消费者的效用函数为u(w)=−ae+c,则他的绝对风险规避系数为:(A)a(B)a+b(C)b(D)c解:B.计算过程为2−bwu′′(w)−abeR(w)=−=−=bau′(w)abe−bw−cw2.证明:若一个人的绝对风险规避系数为常数c,则其效用函数形式必为u(w)=−e,这里w代表财产水平.(这个结论是有问题的,见证明结果)证明:由已知得u′′(w)R(w)=−=cau′(w)u′′(w)dw=−cdw~∫∫−cw+C−cw因此u′(w)⇒lnu′(w)=−cw+C⇒u′(w)=e=Ce⇒~C−cwu(w)=−e+C1~Cc,其中C=e>0,C1为任意实数.如果c>0,根据效用函数可单调变换的性质,该偏好可以用效用函数形式−cw−cwu(w)=−e表示.如果c<0,那么该偏好可以用效用函数形式u(w)=e表示.23.若一个人的效用函数为u=w−αw,证明:其绝对风险规避系数是财富的严格增函数.证明:直接运用绝对风险规避系数的定义:u′′(w)2α1Ra(w)=−=w≠u′(w)1−2αw,当2α时.1w≠因此,当2α时,2dRa(w)−(2α)=−>0()2dw1−2αw,即,绝对风险规避系数是财富的严格增函数.4.设一种彩票赢得900元的概率为0.2,而获得100元的概率为0.8.计算该彩票的期望收入.若一个人对该彩票的出价超过彩票的期望收入,请写出这个人的效用函数形式.(形25
第四讲VNM效用……式不唯一)解:最方便的一个形式就是有常绝对风险规避系数的效用函数形式,比如wu(w)=e5.证明:在下列效用函数中,哪些显示出递减的风险规避行为:()β5.1.u(w)=w+α,α≥0,0<β<1.β−2u′′(w)β(β−1)(w+α)1−βdR(w)R(w)=−=−=aa′β−1<0由u(w)β(w+α)w+α,得到dw,因此该效用函数显示出递减的风险规避行为.5.2.u(w)=wdR(w)a()=0Rw=0由a,知dw,因此该效用函数不显示出递减的风险规避行为.5.3.u(w)=ln(w+α),α≥0−12u′′(w)(w+α)1R(w)=−=−=dR(w)aau′(w)1w+α<0由w+α,得到dw,因此该效用函数显示出递减的风险规避行为.35.4.u(w)=wu′′(w)6w2dR(w)R(w)=−=−=−a>0a2由u′(w)3ww,得到dw,因此该效用函数不显示出递减的风险规避行为.6.一个具有VNM效用函数的人拥有160000单位的初始财产,但他面临火灾风险:一种发生概率为5%的火灾会使其损失70000;另一种发生概率为5%的火灾会使其损失120000.他的效用函数形式是u(w)=w.若他购买保险,保险公司要求他自己承担前7620单位的损失(若火灾发生).什么是这个投保人愿支付的最高保险金?(需要补充的条件为:两种火灾的发生是相斥事件)解:如果保险人不购买保险,他不发生火灾损失的概率为他的期望效用水平为Eu(w)=0.9×160000+0.05×90000+0.05×40000=3853同时,他愿支付的最高保险金I,就是使他在支付前后效用水平相等的保险金.E′wII即有()=0.9×160000−+0.1×1600000−7620−=3853一般的假定是,如果决策者在选择间无差异的时候,就表示他在做一个随机决策,也就是说,任何决策都是可以接受的.反过来,假定决策者在选择间无差异时,却出现了他不愿意选择某一个决策的情况,那就是说明他在决策间不是无差异的.26
第四讲VNM效用……解得:I=22008,-141280.125(舍去)即,投保人愿意付的最高保险金为22008元.7.考虑下列赌局10000元1000元0元支赌10.100.900.00付局20.200.600.2030.020.060.9240.010.090.90上表内,矩阵中的数字代表每一种结果的发生概率(比如,在赌局1中,发生10000元的概率为0.1).如果有人告诉你,他在赌局“1”与“2”之间严格偏好于“1”,在赌局“3”与“4”之间严格偏好于“3”.请问他的选择一致吗?请做出说明.说明:他的选择是一致的.设该赌徒的效用函数为u(w),设它原来的财富为零(初始财富量不影响分析结果,后面会看到.)那么Ew1=0.1×10000+0.9×1000=1900,2σ(w)=E(w−1900)=300011同理可得Ew2=2600,σ(w2)≈3352.7从σ(w1)<σ(w2),Ew12(1−P)000(0,1]无论P取上的哪个值,这个等式都是成立的.(当P=0时,这个等式恒不成立)2(1−P)∈[0,2)P⋅x∈[2,+∞)因此,.综上所述,.9.一个消费者具有VNM效用函数,他面临四种结局:A、B、C、D.其偏好序为AfBfCfD.试验显示,他认为B=0.4A+0.6DC=0.2B+0.8D(这里的等号表示“无差异”)请对A、B、C、D四种结局构筑出一组VNM效用值.解:令uA=1,uB=0,(由连续性公理)有uB=0.4uA+0.6uD=0.4u=0.2u+0.6u=0.08CBD10.近年来保险业在我国得到迅速发展,本题应用经济学原理分析为什么人们愿意购买保险.假定有一户居民拥有财富10万元,包括一辆价值2万元的摩托车.该户居民所住地区时常发生盗窃,因此有25%的可能性该户居民的摩托车被盗.假定该户居民的效用函数为u(w)=lnw,其中w表示财富价值.28
第四讲VNM效用……10.1.计算该户居民的效用期望值.解:Eu(w)=0.25×ln80000+0.75×ln100000=2.82+8.63=11.4510.2.如何根据效用函数判断该户居民是愿意避免风险,还是爱好风险?解:利用绝对风险规避系数来计算,具体地,由−1u′′(w)w21R(w)=−=−=>0au′(w)1ww,(w>0)可以得到该户居民是愿意避免风险的.10.3.如果居民支付一定数额的保险费则可以在摩托车被盗时从保险公司得到与摩托车价值相等的赔偿.试计算该户居民最多愿意支付多少元的保险费.解:思路同第六题.该户居民最多愿意支付的保险费就是使他的期望效用在支付前后不变的保险费.设保险费为I,有11.45=ln(100000−I)⇒I≈6099元即该户居民最多愿意支付的保险费是6099元.10.4.在该保险费中“公平”的保险费(即该户居民的期望损失)是多少元?保险公司扣除“公平”的保险费后的纯收入是多少元?解:公平保险为0.25×20000=4000元.保险公司扣除公平保险费的纯收入R的期望值为E(R)=0.75×4000+0.25×(4000−20000)=011.下列三个说法对吗?请说明理由.11.1.摸彩票的期望收益低于消费者付出的货币,而消费者却常常热衷于此,说明在这种情况下,摸彩票的人是喜爱风险的.对.11.2.一个人面对两种收入可能,一种是获得2000元和1000元收入的概率均为0.5,另一种是获得2500元和500元收入的概率各为0.5,两种情况的期望收入相同,故消费者对二者的评价相同.不全面.它没有考虑风险问题.假如消费者对不同的风险水平不是无差异的,这两种收入可能的风险是不一样的(比如,它们收入的标准差是不一样的),因此,消费者对二者的评价不一定会相同.0.511.3.一个消费者的效用函数为u(w)=w,有两种可能的收益,第一种是获得4元和25元的概率均为0.5,另一种情况是他获得9元和16元的概率分别为0.4和0.6,则他对第一种的评价好于第二种.错.在第一种情况g1下,u(g)=Eu(w)=0.5×ln4+0.5×ln25≈0.69+1.61=2.31在第二种情况g2下29
第四讲VNM效用……u(g)=Eu(w)=0.4×ln9+0.6×ln16≈0.88+1.66=2.54.2即他对第二种的评价好于第一种.12.一个人具有期望效用函数,其效用函数的原形是u(w)=lnw.他有机会参与掷硬币,头面向上的概率均为π.如果他下赌注x元,若头面向上,他会拥有w+x;反之,若1π=背面向上,则他只拥有w−x.请解出其作为π的函数的最优赌注x量.当2,什么是他的关于x的最佳选择?解:设掷硬币为赌局g.那么该赌局的效用u(g)=Eu(⋅)=πln(w+x)+(1−π)ln(w−x)(使u(g)最大化的x所满足的一阶条件为:π1−π(−(=0w+xw−x(解得x=2πw−w.又x≥0,因此他的最优赌注为:⎧(1x=2πw−w1≥π≥⎪⎪2⎨⎪(1x=0>π≥0⎪⎩21π=当2时,直接应用前面得到的结果,得出他的最佳选择是x=0.13.一个人具有期望效用函数,其效用函数原形为u(w)=w.他的财产初值为4元.他拥有一张奖券,该奖券值12元的概率为0.5,值零元的概率为0.5.什么是这个人的期望效用?若要他出让该彩票,他索取的最低价会是多少?解:拥有这张奖券意味着参加了抽奖的赌局,设该赌局为g.他的期望效用为u(g)=0.5×4+12+0.5×4=3若让他出让该彩票,他索取的最低价应当是使他出让前后效用水平不变化的价格,设该价格为p,有4+p=3u(w+p)=u(g),即解得p=5.即他索取的最低价会是5元.30
第四讲VNM效用……1u(w)=−14.一个人具有期望效用函数,其效用函数原形为w.他有机会参加一场赌博,若赢了,他的财产会达到w1,赢率为P;但该赌局下他的财产为w2的概率为1−P.为w使他对持有当前财产与参与赌博无差异,则他当前的财产水平0应该是多少?解:对持有当前财产与参与赌博无差异,也就是说,有1⎛1⎞⎛1⎞−=⎜−⎟P+⎜−⎟()1−P⎜⎟⎜⎟www0⎝1⎠⎝2⎠解得P(1−P)w=0(1−P)w+Pw12P(1−P)w=0(1−P)w+Pw即,当前财产水平应当为12时,才使他对持有当前财产与参与赌博无差异.31
第五讲风险规避……第五讲风险规避、风险投资和跨期决策1.一个农民认为在下一个播种的季节里,雨水不正常的可能性是一半对一半.他的预期效用函数的形式为11=lny+lnyNBB预期效用22y这里,NB与yB分别代表农民在“正常降雨”与“多雨”情况下的收入.1.1.假定农民一定要在两种如下表所示收入前景的谷物中进行选择的话,会种哪种谷物?谷物yNByB小麦28000元10000元谷子19000元15000元u解:设种小麦(wheat)和谷子(rice)的效用分别为w和ur,有11Eu=ln28000+ln10000≈9.725w22,同理可得Eur≈9.734Eu>Eu有rw,因此他会选择种谷子.1.2.假定农民在他的土地上可以每种作物都播种一半的话,他还会选择这样做吗?请解释你的结论.解:设农民这样播种的效用为u1,有128000+19000110000+15000Eu=ln+ln≈9.749112222因为Eu1>Eur,因此他会选择这样做.我的解释:根据他的效用函数,农民是风险规避的.因此,能降低风险的组合,只要预期收入属于一定范围内,农民会更偏好能降低风险的组合.每种作物播种一半就是这样的情况.1.3.怎样组合小麦和谷子才可以给这个农民带来最大的效用?解:解线性规划问题11maxln[28000S+19000(1−S)]+ln[10000S+15000(1−S)]S∈[0,1]2232
第五讲风险规避……其中S是小麦在组合中所占的比例.(满足最大化的S值S必定满足的一阶条件为:90005000(−(=019000+9000S15000−5000S(4S=解得9.45即,使小麦占9,谷子占9的组合能给他带来最大效用.1.4.如果对于只种小麦的农民,有一种要花费4000元的保险,在种植季节多雨的情况下会赔付8000元,那么这种有关小麦种植的保险会如何改变农民的种植情况?u解:考虑选择只种小麦并投保的农民的效用wI11Eu=ln(28000−4000)+ln(10000−4000+8000)≈9.816wI22u在1.3中,最佳比例的效用值约为9.7494,小于wI.因此,这个保险会使农民都种小麦.*2.证明:如果一个人拥有初始财产w,他面临一场赌博,赌博的奖金或罚金都为h.赌博的赢输概率都为0.5(公平赌博).若这个人是风险厌恶型的,则他便不会参加该赌博.证明:风险厌恶型意味着u(g)1,()<0Eu[]g()mP,w+f>Eu[]g()P,w+mf00,即罚金按比例增加在防止非法停车上更有效.4.在固定收益率为r的资产上投资w美元,可以在两种状态时获得w(1+r);而在风险资**产上的投资在好日子收益为w(1+rg),在坏日子为w(1+rb),其中rg>r>rb.通过上述假定,风险资产上的投资就可以在状态偏好的框架中被加以研究.4.1.请画出两种投资的结果.4.2.请说明包含无风险资产与风险资产的“资产组合”这样可以在你的图中得到显示.你怎样说明投资在风险资产中的财富比例?4.3.请说明个人对于风险的态度会怎样的决定它们所持有的无风险资产与风险资产的组合.一个人会在什么情况下不持有风险资产?5.设题4中的资产收益要上交税收.请说明(用文字):5.1.为什么对财富按比例征税不会影响配置只在风险资产上的财富比例5.2.假定只有从安全资产中获得的收益才按比例交税.这会怎样影响风险资产在财富中的比例?哪些投资者可能受这样一个税收的影响最大?5.3.如果所有的资产收益都要按比例交收入税,你对5.2的回答会怎样变化?4题和5题的答案在后面.1u(c,c)=cc2c6.某消费者的效用函数为0101.这里0表示其在时期0的消费开支,c1达标其在时期1的消费开支.银行存贷利率相等且为r,该消费者在t=0期的收入为I=600,在t=1的收入I1=100.问6.1.如果r=0,他该储蓄还是借贷?I1I+=I+I=160001解:他的财富现值为1+r,解线性规划maxu(c,c)01c0,c1c1s.t.c+=c+c=1600011+r320160c=c=00得,3,3c−I>0因为00,因此,他该借贷.34
第五讲风险规避……6.2.如果r=1,他该储蓄还是借贷?解:解线性规划maxu(c,c)01c0,c1cI11s.t.c+=I+=1100022220220c=c=00得,3,3c−I>0因为00,因此,他还是该借贷.7.一个人拥有固定财富w,并把它分配在两时期的消费中,个人的效用函数由u(c1,c2)给c2w=c+1出,预算约束为1+r,这里r是单期利率.MRS=1+r7.1.证明如果个人在此预算约束下要最大化其效用,则它应当选择1,2时c1与c的组合.2证明:解线性规划maxu(c,c)12c0,c1c2s.t.c+=w11+r((使u最大化的c1,c2必然满足((((((∂u(c1,c2)∂u(c1,c2)du(c,c)=dc+dc=01212∂c∂c12((((MU1(c1,c2)dc2MRS(c,c)=((=−1,212MU(c,c)dc即21211c2c+=w1同时由约束条件1+r,得到dc2dc+=011+rdc2−=1+rdc即12((MRS(c,c)=1+r由1式和2式,得到1,212.结论得证.35
第五讲风险规避……∂c∂c21≥07.2.证明∂r,但是∂r的符号不确定.c2c=w−1u(c,c),有证明:由约束条件,得1+r,代入12⎛c2⎞u=u⎜w−,c2⎟⎝1+r⎠使u最大化的c2,和r必然满足uuc112du=−dc+dr+udc=022221+r()1+r也就是dcuc212=dr()()1+r[]u−1+ru12∂c2因为u1c2≥0,但u1−(1+r)u2的符号不定,因此∂r的符号不确定.c=()1+r()w−c,代入u(c,c),有由约束条件,得2112u=u[]c,(1+r)(w−c)11使u最大化的c1,和r必然满足du=udc+(w−c)udr−(1+r)udc=0111221也就是dc(c−w)u112=dru−()1+ru12∂c1()c−wu≤0,但u−(1+r)u的符号不定,因此∂r5因为1212的符号也不确定.8.一个人寿保险推销员说:“在你这个年纪购买一张100000美元终身寿险保单比一张定期保单要好得多.持有终身寿险保单,你只在前4年里每年支付2000美元,但在你生命的以后的日子里就无须支付了.一张定期保单每年需要你支付400美观,而且永远是这样.如果你再活35年,你只须对终身保单支付8000美元,但对定期保单则要支付14000美元,所以终身保单无疑是笔更好的交易.假定推销员的寿命预期是正确的,你将如果评价他的论断?更确切地说,假定利率为10%,请计算两张保单的保费成本的贴现现值.5这是个与题目的结论不同的答案.事实上,我认为题目是有问题的——正如我所证明的一样.36
第五讲风险规避……解:如果他的预期是正确的,终身保单的现值为32000100000PV=−∑+≈−3059p()y()34y=01+r1+r定期保单的现值34400100000PV=−∑+≈329f()y()34y=01+r1+r定期保单更划算.9.一个强行推销汽车贷款的女推销员对一个刚刚购车的人说:“假定你用现金购买这辆10000美元的汽车,因为你用那笔钱可在银行获得10%的利率,所以三年内你将至少损失3000美元.另一方面,如果你要选择我们的低成本的汽车贷款购买10000美元的汽车,那么只需每月支付350美元持续36个月即可,总体上你只需为汽车支付12600−10000=2600美元的利息.因此,你通过这样融资就可以省钱.”你是如何评价这一说法的?汽车贷款果真是低成本之举吗?r解:仍通过现值计算.现金支付的现值−10000.年利率为10%,那么月利率m可以()121+r=1.1r≈0.0079计算为m,得到m,那么36个月连续支付350美元的现值为35350−∑≈−11106()mm=01+rm.因此,这个推销员的建议是没有理由的.10.某人计划花1万元去旅游,其旅游的效用函数为v(w)=lnw,这里w为其支出的价值量.如果他在旅途中丢失1000元的概率为25%,他如想为丢钱的损失买保险,且保险价是公平价,则他愿为这1000元损失支付的最高保险金为多少?解:保险公司的价格为公平价,即为购买R的保险,损失后的赔付为0.25R.因此他的期望效用为Eu()w=0.25ln(10000−0.25R−1000+R)+0.75ln(10000−0.25R)他的问题是0.25ln()10000−0.25R−1000+R+0.75ln(10000−0.25R)≥0.25ln9000+0.75ln10000解得(这个不等式方程我实在解不出来)说明一下:个人感觉本题的目的是考察风险规避和公平保险条件下的最优保险金额,但是提的问题感觉偏离了这个意图.()0.40.6uc,c=cc,在第一期和第二期的收入分别为100元和18011.消费者的效用函数为1212元,利率为r.求:11.1.第一期和第二期的消费分别是多少?37
第五讲风险规避……解:(题目假定消费者能自由借贷)消费者的问题可以表述为:maxu()c,c12c2180s.t.c1+=100+1+r1+r6由于消费者的效用函数是Cobb-Douglass形式的,可以直接解得第一期和第二期的消费,⎛180⎞0.6⎜100+⎟⎛180⎞⎝1+r⎠()0.4⎜100+⎟c2==601+r+108⎝1+r⎠721c==40+111+r,1+r11.2.r取什么值时,该消费者在第一期储蓄、贷款或不借贷?72c=40+<1001解:当期消费小于收入则储蓄.令1+r,则该消费者在第一期储蓄.解得r>0.2.72c=40+=1001同理,令1+r,得r=0.2时,消费者不借贷;令72c=40+>10011+r,得r<0.2时,消费者贷款.11.3.当利率变化对c1和c2的影响是什么?dc721=−<0()2解:由dr1+r,得第一期的消费额变动与利率变动方向相反.dc2=60>0由dr,得第二期的消费额变动与利率变动方向相同.12.一个人买了一打鸡蛋,并一定要把它们带回家.尽管回家的旅行是无成本的,但在任何一条路上所带的鸡蛋被打破的概率都是50%.这个人会考虑两个战略.第一个战略:走一条路带所有12个鸡蛋.第二个战略:走两条路,每次带6个鸡蛋.结果(未打碎的鸡蛋)012可能性0.50.56请参考《十八讲》25页.38
第五讲风险规避……12.1.请列出每种战略的可能结果与每种结果的可能性.请说明在每种战略下,回家之后平均都有6个鸡蛋没有被打碎.解:战略一:结果(未打碎的鸡蛋)0612平均打碎的鸡蛋个数为可能性0.250.50.250×0.5+12×0.5=6(个)战略二:平均打碎的鸡蛋个数为0×0.25+6×0.5+12×0.25=6(个)12.2.画一图表示在每种战略下可获得的效用,人们会倾向于哪一个战略?解,如图效用战略二战略一未打碎的鸡蛋0612如果人们是风险规避的偏好,他们的个人效用函数是凹函数.如图所示,他们将选择39
第五讲风险规避……战略二.12.3.采用多于两条路的方案,效用是否可以被进一步改善?如果其他的路是由成本的,那么这种可能性会受到什么样的影响.解:直观地,如果方案多于两条路,效用可以被进一步的改善.(可以参考本章最后一段)如果其他路是有成本的,那么这种可能性将减小.13.判断:下列说法对么?为什么?13.1.当利率上升时,原来的贷款者仍将贷款,而且贷款数量一定会增加;当利率下降时,原来的借款者将继续借款,而且借款数量至少不会减少.答:这里假定,消费的收入效应为正.第一句错误.因为利率上升除了带来跨期间的替代效应(倾向增加贷款,至少不会减少贷款),也会带来贷款者财富的增加,这将倾向于增加当期的消费,产生减少贷款的因素.因此不能确定原来的贷款者将贷款.第二句正确.因为利率下降无论是跨期间的替代效应(倾向增加借款,至少不会减少借款),还是收入效应(财富增加导致当期的消费量增加,因此倾向于增加借款)对借款的影响都是非负的.如果某一期的收入效应不确定正负(理论上是可能的),那么两句话都是错误的,分析方法完全相同.13.2.跨期消费的第一期和第二期的消费之间的边际替代率为1+r.答:正确.消费者效用最大化的标准为边际替代率等于价格之比,若令第一期商品价1格为1,那么第二期商品的价格为1+r.p11MRS===1+r1,2p121+r由此可知其正确性.13.3.如果名义利率小于通货膨胀率,则一个理性的消费者不会选择存钱.答:错误.考虑这个理性消费者只在第一期有收入,无论名义利率如何,他不存钱,第二期就会饿死.消费者是否存钱取决于他第一期的收入是否大于第一期最优消费额,第一期的收入是先在决定的,利率只能部分地影响最优消费者,利率不能完全左右这个关系.14.在一个封闭的村庄里中唯一的产品是玉米,由于土地的原因好收成与坏收成交替出现,今年的收成是1000公斤,明年的收成是150公斤,这个村庄与外界没有贸易.玉米可u(c,c)=cc,c是今年的消费,c以储存但是老鼠会吃掉25%,村民的效用函数为121212是明年的消费.14.1.画出跨时期预算曲线,指出截距位置.40
第五讲风险规避……c2(0,900)(1000,150)c114.2.村民今年消费量是多少?此题与11题的计算方式完全相同,所不同的是,因为老鼠的参加使利率r=−0.25,再有,今年消费不能超过1000公斤.解:(方法类似11题)消费者的问题是maxu(c,c)12c2s.t.c1+=1200,c1≤10000.75解得:c1=600(公斤)即,村民今年消费600公斤玉米.14.3.老鼠吃掉多少?解:根据14.2的结果,村民将储存1000−600=400公斤玉米,其中400×25%=100公斤玉米被老鼠吃掉.14.4.村民明年消费多少?解:把14.2解完,得到c2=450(公斤),即村民第二年吃450公斤玉米.41
第五讲风险规避……第五讲,第4题wgABwb第一问,第二问基本上的图就是这样,A点为将财富全部投入到风险投资时的状态,B点为全部投入到安全资产时的状态,以这两点为端点的线段表示的就是投资者所有可能的资产组合.第三问见第5题的解答.第五讲,第5题设投资者的效用函数为u(w).设wg为投资者在好的状态下的财富,wb为坏状态下的财富.设投资者认为有P的概率出现好的状态.设λ∈[0,1]为风险资产在投资组合中所占比例.由题意知,投资者决定λ是以u的最大化为标准.即:*λ∈argmaxu(w,λ)λ∈[0,1]7du(·)=0因此,λ必须满足dλ*又7事实上,很明显这个集合里面至多只有一个元素.42
第五讲风险规避……*[**]u(w,λ)=Pu(w+(1−P)u(w)=Puλ(1+r)w+(1−λ)(1+r)wgbg[]**+(1−P)uλ(1+r)w+(1−λ)(1+r)wg代入(*)得,du(w)gdw1−Prb−r=−·=kdu(wb)Prg−rdw**du(w)gdwdu(w)b现在证明dw是λ的单调函数.u′wu′′w若()>0,()<0***jijijiuwgλ>uwgλu[w(λ)]λ则有[()][()],bbjidu[w(λ)]du[w(λ)]ggdwdw>jidu[w(λ)]du[w(λ)]bb由假设(***)知,必然有dwdw(即为λ的单调递增函数)也就是说,等式(**)决定了唯一一个最优风险资本比例λ.du(w)gdwdu(w)b如果k值并不在dw的值域内,事实上就说明,投资者将选择纯风险投资,即λ=1,如果k=1,那么,投资者将选择λ=1(这解答了第4题的第三问)第一问du(wg,tw)(1−t)du(wg)du(wg)dwwdwdw==du(w)du(w)du(w)b,tw(1−t)bbtwdwwdw设对财富按比例征税的税率为,那么dw,而仍然对应原有的风险资产比例λ,风险资产的比例不变.第二问t设对安全资产的收益按比例征税的税率为s那么du(w)g,tsdw1−Prb−r+ts+rts1−Prb−r=−·>−·=kdu(wb,ts)Prg−r+ts+rtsPrg−rdw所以,如果考虑对安全资产的征税,风险资产比例λ应该增加.这对只投资无风险资产的投43
第五讲风险规避……资者的影响最大.第三问t设对安全资产的收益按比例征税的税率为s,对风险资产收益按比例征税的税率为tr.du(w)g,ts,trdw1−Prb−r−tr−rgtr+ts+rts=−·du(wb,ts,tr)Prg−r−tr−rgtr+ts+rts那么dw−t−rt+t+rt>0结果是,如果rgrss,那么最优风险资产比例λ应该上升,如果−t−rt+t+rt<0−t−rt+t+rt=0rgrss,那么最优λ应当下降,rgrss时,最优λ应当保持不变.44
第六讲生产函数……第六讲生产函数与规模报酬21.生产函数为Q=−KL+16L−18,工人工资为w=8,产品价格为p=1.计算:1.1.短期内K=2,最优劳动投入是多少?解:短期内生产函数为2Q=−2L+16L−18S,S表示短期.厂家的问题是maxπ(L)SL≥0其中()2πL=pQ(L)−wL=−2L+8L−18SS(解决这个问题的劳动最优投入量L满足一阶条件dπ(S=−4L+8=0dL因此((L=2(L≥0,因此符合约束条件)即,最优劳动投入为2.1.2.最大平均产量的劳动投入为多少?此时的最大平均产量是多少?解:这个问题可以表述为:Q(L)SmaxL≥0LQ其中,S同1.1.解决这个问题的劳动投入量Lˆ满足一阶条件d⎛QS⎞18⎜⎟=−2+=0dLLLˆ2⎝⎠即Lˆ=310即,人均产量最大的劳动投入为3,此时的最大平均产量为3.45
第六讲生产函数……2.确定下列函数是不是齐次函数,如果是,规模报酬情况如何?()332.1.fx,y=x−xy+yr解:因为∃t>0,使得对∀r∈R,f(tx,ty)=tf(x,y)在R2上都不成立.所以,它不是齐次函数.比如t=2时,()()r(r)3(r)(r)3f2x,2y−2fx,y=8−2x−4−2xy+8−2y=0恒成立的条件是,∃r∈R,使得rr8−2=4−2=0即8=4r而8=4是不可能的.因此对∀r∈R,f(2x,2y)=2f(x,y)在R2上都不成立,这就证明了前面的结论.12.2.f()x,y=2x+y+3()xy211解:因为对∀t>0,都有f()tx,ty=2tx+ty+3t()xy2=tf()x,y,所以它是一次齐次函数,规模报酬不变.1432.3.f()x,y,w=()x−5yw22f()tx,ty,tw=t3f(x,y,w),因此,它是齐次函数.当t>1解:因为对∀t>0,都有时,有f(tx,ty,tw)1,令f()tK,tL=tf(K,L),有47
第六讲生产函数……11β+βt()KL2+βtK+βtL=tβ+βt()KL2+βtK+βtL01230123β=tββ=0即,对∀t>1,有00,因此0时,该生产函数呈现规模报酬不变.4.2.证明在规模报酬不变的情况下,该函数呈现出边际生产力递减而且边际生产力函数是零次齐次的.1f(K,L)=β()KL2+βK+βL解:对1231∂f1⎛L⎞2MPK()L,K==β1⎜⎟+β2有K的边际生产力∂K2⎝K⎠则MPK()tL,tK=MPK()L,K即函数对K的边际生产力函数是零次齐次的.231df1−=−βK2L2<021又dK4,即K的边际生产力递减同样可以得到L的边际生产力函数一次齐次和递减.5.判断下列结论是否正确,并说明理由:5.1.边际产出大于零,则总产量将随着投入的增加而上升,平均产量则不一定上升.答:边际产出大于零,即多增加一个单位的投入,总产出的增量为正,即总产量将随着投入的增加而上升.如果多增加一个单位的投入,总产量的增量高于平均产量,那么平均产量在增加该单位的投入后将上升,但是,也可能出现总产量增量在为正的同时低于平均产量的情况(因为平均产量严格大于零),那么平均产量在增加该单位的投入将上升.5.2.如果生产是有效率的,生产的可能性边界一定是外凸的.答:假设一个经济生产的产品包括q1,q2,利用唯一的生产要素x;生产可能性边界可以表述为x=h()q,q12范围经济生产有效率,必然有联合经营所需要素投入低于分别经营要素投入量总(αq,()1−αq,h(αq,(1−α)q))是有效率的生产,必有:和.即,如果1212h()αq,0+h(0,(1−α)q)≥h(αq,(1−α)q)1212h(q,0)+h(0,q)≥h(q,q),这样在生产可如果生产可能性边界是外凸的,必然有1212能性边界上必然存在一个最高效率的生产线.但是,考虑下面的图,绿线是等要素投入线,橙线表示两种产出的(消费者)边际替代率.尽管A点是有效率的,但是,它所在的生产可能性边界不是外凸的.它是一个凹集.48
第六讲生产函数……q2Ah(q,q)=x12q1即,生产有效率并不是一定意味着生产可能性边界外凸.1y=L3,产出品价格p=3,工资率w=4,固定资本成6.假定一家企业的生产函数为本为2.*6.1.求最优要素投入量L1π()L=pL3−wL−2,最大化的一阶条件是解:企业利润*dπ()L1*−23=pL−w=0dL3*1L=代入p=3,w=4,解得8.又2*dπ()L2*−53=−pL<02dL9.*11L=因此函数在8取得最大值.即最优要素投入量为8.6.2.最优供给量*1*1L=y=解:当8时,产出2.6.3.计算这家企业的利润量.*1()*3*解:πL=pL−wL−2=−16.4.这家企业应不应关闭?49
第六讲生产函数……答:应该,因为它无法取得非负的利润.7.证明:若某家企业的生产函数为ALα,(0<α<1),如果该企业的资本支出为一常数J,则7.1.其供给量q随产品价格p上升而上升.()α证明:设该企业的工资率为一常数w,则它的利润πL=pAL−wL−J最大化的1dπ()L*α−1*⎛αpA⎞1−α1=αpAL*−w=0L=⎜⎟>0一阶条件是dL,即⎝w⎠,因为1−α,所以**L是p的增函数,又生产函数是L的增函数,所以供给量随产品价格p上升而上升.7.2.q随工资率w上升而下降1*⎛αpA⎞1−αL=⎜⎟证明:从⎝w⎠知,L*是w的减函数,又生产函数是L*的增函数,因此q随工资率w上升而下降.111F()K,L=4K2L4,产品价格为1,工资率为48.已知一家企业的生产函数为,利率为12.固定资本成本为k.8.1.求L:K的最优比率.1111π()K,L=4K2L4−L−K−k解:企业利润42最大化的一阶条件为()**11*∂πK,L*−41F1=2K2L−=−=0*∂K22K2**13*∂π()K,L*−1F1=K2L4−=−=0*∂L44L4*F1*2K=2*1F*即有4L4,即L:K最优为1:18.2.求L与K的最优量.50
第六讲生产函数……113***F()K,L=4K2L4,有**4解:由上一问的解,可以得到K=L=F,代入F=4F,***解得F=256.因此K=L=256.9.某公司有甲、乙、丙三分公司,每个分公司都生产X和Y两种产品,下面是三个分公司用其全部资源可生产的X和Y的最大产量.解:(具体数据在书上.)要说明的是,这道题对生产集没有任何限制,甚至没有说明生产集的连续性,因此,这个生产可能性边际曲线甚至可能不存在.10.在落日湾用手挖海蚶只需要劳动投入.每小时可获得的海蚶总量q由下式给出q=100L其中,L是每小时的劳动投入.10.1.用图表示出q与L的关系.q单位100L单位1(刻度不知道怎么标)10.2.落日湾中劳动的平均生产力为多少?用图表示这一关系并表明随着劳动投入的增加AP下降.Lq100AP==L平均生产力为LL.见图上的虚线,它们的斜率表示平均生产力.随着L的增加,这些虚线的斜率减小.说明随着劳动投入的增加,APL减小.51
第六讲生产函数……50MP=L10.3.证明落日湾的劳动边际产出为L用图表示这一关系,并证明对于所有的L值,MPL0,MPL>0;∂K,∂Lα−1βMP=αLK,其中L,K,α均大于零,因此MP>0.而证明:KK2∂q()α−2β=α−1αLK<02∂K,因为0<α<1.KK12.3.证明MRTS只取决于L而不依赖于生产规模,而且MRTS(L对K)随着L的增加而递减.α−1βMPLαLKαKMRTSL,K==αβ−1=KK证明:MPKβLKβL,即MRTS只取决于L,而随着L的增加而递减.13.我们已知,对于欧拉定理(见本讲第五节),它意味着规模报酬不变的生产函数q=f()K,L,有q=fKK+fLL运用这一结论,证明对于这种生产函数,如果MPL>APL,则MPK必为负数.这意味着生产应该在何处进行呢?一个企业能够在APL递增的点进行生产吗?证明:在等式两边同除以K,得qK=f+fKLLLqAP=L其中L,MPL=fL,MPK=fK.因此有:LMP=−()MP−APKLLK因此当MPL>APL时,MPK必为负.这说明生产应当在边际产出大于平均产出的地方进行,也就是,不应当在平均产出达到最低点前进行.这也是最后一个问的答案,一个企业不能在APL递增的点进行生产.14.再次运用欧拉定理证明,对于只有两种投入K和L的一个规模报酬不变的生产函数,54
第六讲生产函数……f必定为正.解释这一结论.KL证明:在q=fKK+fLL两边对L求一阶偏导数.有:=′′+′′fLfKLKfLL即1f=()f−fKLLLLK其中fL大于零,fLL小于零,因此fKL为正.函数的规模报酬不变,这说明产出与有效率的要素总投入量具有线性关系,但是对各个生产要素,同等要素投入增量的边际产出却呈现递减的趋势,这说明一个要素的边际生产能力会受另一个要素投入量提高而提高.15.生产函数形式如下11q=K2L215.1.劳动和资本的平均生产力是多少?11⎛K⎞2⎛L⎞2APL=⎜⎟APK=⎜⎟解:⎝L⎠,⎝K⎠15.2.图示当K等于100时的APL曲线.AP,MPLLL解:这里没有办法标出点(word技术问题),边际产出为红线.11MP=APMP=APLLKK15.3.证明2,2.运用这一信息,加一个MPL函数到2图中,这一曲线有何特别的地方?1∂q1⎛K⎞211MPL==⎜⎟=APLMPK=APK解:∂L2⎝L⎠2,同理2.15.4.画出q=10时的等产量线.55
第六讲生产函数……解:见上图.15.5.运用3的结果,在点K=L=10,K=25,L=4及K=4,L=25处,q=10上的等产量上的MRTS是多少?这一函数呈现边际技术替代率递减吗?解:事实上可以利用12题第3问的结论.在三个点,边际技术替代率(L对K)分别为1,25/4和4/25,这个函数呈现边际技术替代率递减.56
第七讲要素需求函数……第七讲要素需求函数、成本函数、利润函数与供给函数f()x,x=0.5lnx+0.5lnxπ(w,w,p)1.已知生产函数为1212,求利润函数12,并用两种y()w,w,p方法求供给函数12wiMP=i解:(生产函数严格凹,因此)厂家利润最大化的充分必要条件是p,i=1,2,1pMP=x()w,w,p=ii122x2w代入i解得i,i=1,2,因此厂商的利润函数为2pπ()w,w2,p=pf()(x1()⋅,x2()⋅−∑wixi⋅)=plnp−pln2−ln()w1w2−pi=12.1y()(w,w,p=f()x⋅),x(⋅)=lnp−ln()ww−ln2121212厂商的供给函数为2,该供给函数也可以通过利润函数对p求偏导得到.()22.已知成本函数为CQ=Q+5Q+4,求厂商供给函数S(p)与利润函数π()p.解:(成本函数边际成本递增,因此)厂家利润最大化的充分必要条件是MC()Q=p,15S()p=p−代入MC()Q=2Q+5,得到供给函数22,利润函数()()()()12πp=pSp−CSp=p−5p−443.下列说法对么?为什么?()0.5函数πp=p可以成为一个利润函数.答:不对.因为该函数对p不是一次齐次函数,因此它不可以成为一个利润函数.4.在一篇著名的论文里(J.Viner:“CostCurvesandSupplyCurves”.ZeitschriftfurNationalokonomie3(September1931):23–46),维纳批评他的绘图员不能画出一组SATC曲线,并令其与U型AC线的切点也分别是每一条SATC线的最低点.绘图员抗议说这种画法是不可能做出的.在这一辩论中,你将支持哪一方?我支持绘图员.如果AC与所有SATC线最低点相切,那么它将有多个斜率为零的点,57
第七讲要素需求函数……这意味AC上存在二阶导数为零的点(微分中值定理).又AC是U型,即二阶导数恒大于零的.这两者是矛盾的.5.施教授与纪教授将出版一本新的初级教科书.作为真正的科学家,他们提供了写作该书的生产函数如下11q=S2J2其中q=完成该书的页码数,S=施教授将要支出的工作时间(小时)数,J=纪教授花费的工作小时数.施教授认为其每小时工作价值为3美元,他花费了900小时准备初稿.纪教授的每小时工作价值为12美元,并将修改施教授的初稿以完成此书.5.1.纪教授必须花费多少小时,以完成一本具有下列页数的书:150页?360页?450页?11q=S2J2,得到纪教授必须花费的时间分解:将q=150,360,450与S=900代入别为25小时,144小时和225小时.5.2.一本150页的成书的边际成本是多少?300页的书的边际成本是多少?450页的书的边际成本是多少?解:当S=900时,该书的生产成本函数为22()⎛q⎞qCq=3S+12J=2700+12⎜⎟=2700+⎝30⎠75它的边际成本为2MC()q=q75代入q=150,300,450代入上式,得边际成本分别是4美元,8美元和12美元.6.假定厂商生产函数为柯布-道格拉斯生产函数,有αβq=KL,其中α,β>0厂商可以在竞争性投入市场购买租金价格分别为v与w的任意数量的K与L.6.1.证明成本最小化要求vK=wLαβ该厂商的生产扩张县的形状是什么MPwL=αβ−1α−1β证明:成本最小化要求MPKv,代入MPL=βKL,MPK=αKL,即得到结论.αwK=L因为βv,因此该厂商的生产扩张线是一条射线.6.2.假定成本最小化,证明总成本可以表示为下述的关于q,v与w的函数.58
第七讲要素需求函数……1βαα+βα+βα+βTC=Bqwv这里,B是依赖于α与β的常量.αwK=Lαβ证明:代βv入q=KL中,得到α⎛αw⎞α+βq=⎜⎜⎟⎟L⎝βv⎠,解出α1−α+β⎛αw⎞α+βL=q⎜⎜⎟⎟⎝βv⎠α1−α+β⎛αw⎞α+βαwL=q⎜⎜⎟⎟K=L将⎝βv⎠代入βv,得到β1α+β⎛αw⎞α+βK=q⎜⎜⎟⎟⎝βv⎠因此生产成本就可以表示为⎡βα⎤1βαα+βα+βα+β⎢⎛α⎞α+β⎛β⎞α+β⎥qwv⎢⎜⎜⎟⎟+⎜⎟⎥⎝β⎠⎝α⎠C=vK+wL=⎢⎣⎦⎥βα⎛α⎞α+β⎛β⎞α+βB=⎜⎜⎟⎟+⎜⎟令⎝β⎠⎝α⎠,则得到欲证结论.7.假定厂商固定要素比例的生产函数如下q=min(5K,10L)资本与劳动的租金价格分别为v=1,w=3.7.1.计算厂商的长期总成本、平均成本与边际成本.解:厂商的要素需求函数为qqK=L=5,10q1LTC()q=因此长期总成本为2,平均成本和边际成本恒为2.7.2.假定K在短期内固定为10,计算:厂商的短期总成本、平均成本与边际成本,第1059
第七讲要素需求函数……单位的边际成本是多少?第50单位呢?第100单位呢?(prettyboring)解:厂商的短期生产函数为⎧10L0≤L≤5q=⎨50L>5⎩因此,厂商的短期总成本为⎧3⎪q+100≤q≤50STC()q=⎨10⎪⎩+∞q>50平均成本为⎧310⎪+0≤q≤50SAC()q=⎨10q⎪⎩+∞q>50边际成本为⎧3⎪0≤q≤50SMC()q=⎨10⎪⎩+∞q>50由此,可以得到第10和第50单位的边际成本为0.3,而第100个单位的边际成本为正无穷大.8.假定某曲棍球生产厂商的生产函数是q=2KL在短期,厂商的资本装备数量固定为K=100.K的租金价格为v=1元,L的工资率为w=4元.8.1.计算厂商的短期总成本曲线22qqSTC()q=vK+wL=vK+w=100+解:4K1008.2.厂商的短期边际成本函数是什么?如果生产25个曲棍球棒,则厂商的短期平均成本与短期边际成本是多少?若生产数量分别为50、100与200时,它们又是多少?()100qqSACq=+SMC()q=解:q100,50.由此可得当生产数量分别为50、100和200时,短期平均成本分别为2.5,2和2.5,短期边际成本分别为1,2和4.8.3.画出厂商的短期成本曲线和短期边际成本曲线.标出2中所求的点.SMC60
第七讲要素需求函数……SAC,SMC4SAC2.5210q501002008.4.短期边际成本曲线与短期平均成本曲线在何处相交?解释为什么短期边际成本曲线将通常交于短期平均曲线的最低点.解:两者在短期平均成本曲线最低点相交.当多生产的一单位产品的成本低于平均成本时,平均成本下降;而多生产的一单位产品的成本多于平均成本时,平均成本上升.因此,当多生产一单位产品的成本(即边际成本)等于平均成本时,平均成本最低.9.一个富有进取心的企业家购买了两个工厂以生产装饰品.每个工厂生产相同的产品而且每个工厂的生产函数都是q=KLiii,i=1,2每个工厂在各自拥有的资本存量方面却不同.工厂1拥有K1=25,工厂2拥有K=100.K与L的租金价格由w=v=1元给出.29.1.如果该企业家试图最小化短期生产总成本,则产出应如何在两个工厂分配?5L+10L≥q解:厂商的问题是在12的条件下,最小化L1+L2+125,其一阶条件为L=2L21qL=L=2L5L+10L=q1代21入12得25q4qq=5L=q=q−q=1121因此,5,5.9.2.给定在两个工厂间的最优产量分配,计算短期总成本、平均成本与边际成本曲线.产量为100、125与200时的边际成本为多少?22q4qL=L=11解:由上题知625,625q2125q2qSTC=125+L+L=125+SAC=+SMC=12所以125,同时q125,125.61
第七讲要素需求函数……816因此,产量为100、125与200时的边际成本分别为5,2和5.9.3.在长期,应如何在两个工厂间分配产量?计算长期总成本、平均成本与边际成本.LTC(q)8LMC()q解:设两个工厂的的长期总成本为i,长期边际成本i,又设总产量q=(1−λ)q为q,令q1=λq,2,那么厂商的问题是确定一个λ值,使LTC()λq+LTC[]()1−λq最小.其一阶条件为LMC()λq−LMC[(1−λ)q]=0,因为技术呈现规模报酬不变,LMC(⋅)不变,因此任意λ∈[]0,1均满足该条件,使得总成本最低.成本函数为C(q)=2q,而产量可以在两个厂任意分配.平均成本LAC=2,边际成本LMC=2.9.4.如果两个工厂呈现规模报酬递减,则3将会有什么变化.解:因为两个工厂均呈现规模报酬递减,则它们的长期边际成本随各自的产量增加而单调递增.考察9.3中的一阶条件LMC(λq)−LMC[(1−λ)q]=0,因为LMC()⋅单1λ=调递增,因此这意味着λq=(1−λ)q,即2.10.假定某曲棍球棒厂商的生产函数是q=2KL而资本在短期固定为K.K、L的租金分别为v和w.10.1.计算厂商的总成本为q,w,v和K的函数.2qL=解:当K=K时,4K,此时厂商的(短期)总成本为2qTC()q=vK+w4K10.2.给定q,w与v,资本投入应如何加以选择以使成本最小?8事实上这个假定是不必要的.如果假定两个工厂的生产函数不同,那么最后的结论就是两个厂的边际成本相等的条件隐性地确定了λ的值.62
第七讲要素需求函数……2∂TC21w∂TC21=v−wq=0K=q=wq>0223解:令∂KK,得到一阶条件v.又∂KK,wK=q因此成本最小化的资本投入是v.10.3.用你在2中求得的结果去计算曲棍球棒生产的长期总成本.2qwTC()q=vK+wK=q解:令4K中v,就可以得到曲棍球棒生产的长期总成本5LTC()q=qwv为4.10.4.对于w=4美元,v=1美元,试画出曲棍球棒生产的长期总成本曲线.运用K=100,K=200与K=400证明它是由1所算出的短期成本曲线的包络线.解:此时,LTC()q=2.5q,K=100,K=200与K=400时的短期成本分别为222qqqSTC()q,100=100+STC()q,200=200+STC()q,400=400+100,200,400.画图结果可以参考范里安那本书上的相关内容.11.下列说法对吗?为什么?因为利润最大化是成本最小化的充分条件,所以要素需求函数具有条件要素需求函数的所有性质.答:最好说成“所有共同性质”.成本最小化刻画了所有条件要素需求函数的共同性质,也就是说成本最小化所刻画的条件要素需求的性质属于所有被如此刻画的函数的性质的交集,因此,说要素需求函数首先要满足成本最小化,等价于说要素需求函数首先要满足条件要素需求函数的共同性质.211C()w,r,Y=w3r4y2可以成为一个成本函数么?(这里w是工资率,r是利率,12.函数y为产量.)并请陈述您的理由.答:因为违反了成本关于要素价格具有一次齐次性的要求,它不可以成为一个成本函数.C()r,r,q13.推导成本函数12,当生产函数分别为以下形式时.注:假设每个生产函数都只有一种产出.z1、z2为两种投入,r1、r2分别为两种投入的单价,q为产量.f()z,z=z+z13.1.121263
第七讲要素需求函数……rz+rz=r()q−z+rz=rq+(r−r)z,z∈[0,q]解:1122122212122C(⋅)=rq因此,当r2−r1≤0时,令z2=q,得到2,当r2−r1≥0时,令z2=0,得C()⋅=rq到1.C()⋅=qmin{r,r}综上,12f(){}z,z=minz,z13.2.1212rz+rz≥()r+rq解:因为112212C()(⋅=r+r)q因此成本函数121ρρf()z,z=()z+zρ13.3.1212max()rz+rz解:11221()ρρz+zρ≥qs.t.12一阶条件满足1⎛r⎞ρ−11z=⎜⎟z1⎜⎟2r⎝2⎠,,−1−111⎡⎤⎡⎤⎛r⎞ρ−1⎛r⎞ρ−1⎢⎜1⎟⎥⎢⎜2⎟⎥z=q1+z=q1+2⎢⎜r⎟⎥1⎢⎜r⎟⎥⎝2⎠⎝1⎠代入生产函数,得⎢⎣⎥⎦,⎢⎣⎥⎦,则−1−11ρ−21ρ−2⎡⎤⎡⎤()ρ−1ρ−1ρ−1ρ−1C⋅=q⎢r2+r1r2⎥+q⎢r2+r2r1⎥⎢⎣⎥⎦⎢⎣⎥⎦14.下列说法对么?为什么?14.1.当边际成本下降时,平均成本必下降.1⎡Q⎤[]0,QAC=Q⎢⎣∫0MC()tdt+T⎥⎦答:若MC在上连续.记,那么dAC1⎡Q⎤1=QMC()Q−MC()tdt−T=[]Q()MC()Q−MC()ξ−TdQQ2⎢⎣∫0⎥⎦Q2,其中64
第七讲要素需求函数……dAC<0ξ∈()0,Q(因为边际成本下降),那么有MC(Q)MC(ξ),但是因为有固定成本T使得dQ的符号不能确定.f(z,z)=alnz+alnz,a>0,a>0.计算利润最大化的利15.对于生产函数12112212润函数、供给函数.并判断利润函数是否满足课本上讲过的性质1到4.解:(生产函数为拟凹函数,因此)利润最大化的条件为pf=wwii,其中i=1,2,i为要素i的价格,p为产出价格.paiz=iwy=()a+alnp−alnw−alnw+φ,(φ=alna+alna)解得,i,1211221122π()p,w=()a+aplnp−pa(1+lnw)−pa(1+lnw)+pφi121122.其中y为供给.对性质一的验证:∂π=y>0∂p对性质二的验证:∂π=−z<0i∂wi对性质三的验证:π()tp,tw=()a+atplnp+(a+a)tplnt−tpa(1+lnw)(−tpalnt−tpa1+lnw)i121211122−tpalnt+tpφ2=t()a+aplnp−tpa()1+lnw−tpa(1+lnw)−tφ121122=tπ()p,wi对性质四的验证:f()λx+()1−λx≤λf(x)+(1−λ)f(x),但是这个看起来比较一个办法是根据1212((2))H=f难.还有一个是通过矩阵fij3×3的正定性来判断.但是好麻烦,这里就饶了我吧.估计平老师也不会考这个的.16.求证:在竞争型的市场中,如果一个厂商的生产技术具有规模报酬不变的特性,那么如果最大利润存在,它一定为零.65
第七讲要素需求函数……证明:厂商生产技术规模报酬不变,意味着它没有固定成本;因此,当最大利润为负时,厂商可以选择生产规模为零,使得利润为零.又假设最大利润大于零,那么考虑这个厂商将生产规模扩大一倍.根据竞争性市场的假设,这时产出价格不会变化,总收益为原来的两倍,同时(仍根据竞争性假设)要素价格也不会变化,它和厂商技术规模报酬不变一起决定了总成本等于原来的两倍,这就意味着利润等于原来利润的两倍,也就是说,最大利润如果存在,它不可能大于零.综上,如果最大利润存在,它一定为零.17.说明生产者剩余也能由如下运算得出:*p∫()∂π∂pdp0*这里p是市场给出的价格,企业是价格接受者.说明:无法说明.这仅仅在企业边际成本在q>0上非减才会成立.18.假定一个从事非法复制计算机光碟的长沙国内有如下每日短期总成本函数:2STC=q+2518.1.如果非法复制的计算机光碟每盘卖20元,则这个厂商每天生产多少?它的利润是多少?解:令厂商短期边际成本等于20,即2q=20,得到厂商每天生产10张光碟,其利润为每天75元.18.2.当p=20元时,厂商的短期生产者剩余是多少?解:其生产者剩余等于利润加固定成本,由上题结果知其利润为75元,固定成本25元,因此生产者剩余为100元.18.3.写出这个厂商的生产者剩余作为非法光碟价格的一般表达式.22pp⎛p⎞pq=p−⎜⎟−25=−25解:由边际成本等于价格p,得2,那么利润为2⎝2⎠4,2p加上固定成本得到生产者剩余4.19.给出下列论断不成立的反例.19.1.平均成本在任何地方都递减,意味着边际成本在任何地方都递减.反例:考虑平均可变成本存在最低点,且存在固定成本的情况.这使得边际成本先与平均可变成本最低点相交,然后与平均成本最低点相交.很明显在于平均成本相交之前,边际成本是递增的,而平均成本递减.图形可以参考十八讲122的图7.2.19.2.成本函数呈次可加性意味着平均成本在任何地方都递减.66
第七讲要素需求函数……q反例:如果说成本函数次可加性是定义为存在q1,q2…n,使得∑∑C()q>C(q)ii,那么一个反例就是可以假设一个离散的生产技术.因为递减是建立在函数的连续性上的,因此一个离散的生产函数在满足成本次可加性(这很容易找到)的同时,却没有平均成本的递减.20.学习曲线的出现与规模报酬递增是一回事么?如果不是,请说明两者之间的区别.答:不是(这里答不全).出现学习曲线是规模报酬递增的原因之一,规模报酬递增也会因为一些别的原因,比如更精密的分工和企业内部交易成本的递减等等.21.有学者对美国化工行业的平均成本AC,行业的累积产量X,以及企业平均规模Z做了回归.其计算结果如下:lg()AC=−0.387lgX−0.173lgZ21.1.请你对上述计算结果作出经济解释.这里,什么的学习曲线效应,什么是规模经济效应?它是多少?答:学习曲线效应是等式右边第一项,行业累积产量增加1%,平均成本下降0.387%.而规模经济效应是右边第二项,企业规模每增加1%,平均成本则下降0.173%.21.2.这项研究对于你研究中国工业行业中的学习曲线效应与规模报酬效应有什么启发?若你想做这样的研究,应该首先确定哪些供给指标?对统计数据先做什么样的处理?答:因为没有学过计量,不敢妄下结论.67
第八讲完全竞争与垄断第八讲完全竞争与垄断1.某产品的市场需求曲线为Q=1800−200p.无论什么市场结构,该产品的平均成本始终是1.5.当该产品的市场是完全竞争市场时,市场价格和销量多大?消费者剩余、生产者剩余和社会的无谓损失是多大?当该产品的市场是完全垄断市场时,只能实行单一价格,市场价格和销量多大?消费者剩余、生产者剩余和社会的无谓损失是多大?当该产品的市场是完全垄断市场,同时生产者可以实行一级差别价格,市场销量是多少?消费者剩余、生产者剩余和社会的无谓损失是多少?1.1.平均成本始终为1.5,说明边际成本也是1.5.令市场价格等于边际成本1.5,则得到市场销量为1500.9∫Q()pdp=5625这时,消费者剩余为1.5,生产者剩余为零,社会无谓损失为零.1.2.完全垄断市场上的单一定价意味着厂商将令边际收益9−0.01Q等于边际成本,得到,9Qm=750,pm=5.25,此时消费者剩余为∫5.25Q()pdp=1406.25,生产者剩余为5.25Qm()pm−MC=2812.5,这时社会无谓损失为∫1.5[]Q()p−750dp=1406.25.还有一种计算无谓损失的就是用完全竞争市场的消费者剩余(同时也是社会剩余)减去垄断市场下的消费者剩余和生产者剩余之和.1.3.当垄断者可以实施一级垄断价格时,市场销量为1500,消费者剩余为零,生产者剩余为5625,社会的无谓损失为零.2.一个有垄断势力的企业面临的需求曲线为0.5p=100−3Q+4A总成本函数为2C=4Q+10Q+A2.1.试求出实现企业利润最大化时的A、Q和p的值.[(0.5)(2)]maxQ100−3Q+4A−4Q+10Q+A解:企业的问题是A,Q.0.5−0.5其一阶条件为90−14Q+4A=0,2QA−1=0,解得Qm=15,A=900,p=175这时,m.pm−MC(Qm)9=p352.2.这时,企业的勒纳指数为m68
第八讲完全竞争与垄断2j()pkπp,k=−k3.如果某行业中典型企业的利润函数为16,k为资本规模;市场需求294Q=为P.3.1.求典型企业的供给函数.jjdπpky==解:根据霍太林引理有供给dp8.3.2.求长期均衡价格.jpe.解:长期均衡价格就是使利润等于零的价格,令π=0,得长期均衡价格=43.3.证明:[长期均衡中]行业中单个企业的资本规模k会与行业中存在的企业个数成相反关系.e证明:记长期均衡中市场上存在的企业个数为J.代p=4入需求函数,得到长期Jejpke∑y=J=Qe均衡的市场供给为Q=73.5[零经济利润条件].令市场j=18[市场均e8Q147J==e衡条件],得到pkk.即J与k成相反关系.4.在一个完全竞争,成本不变的行业中有几十个企业,它们的长期成本函数均为32LTC=0.1q−1.2q+111q,其中q是单个企业的年产量,市场对该行业产品的需求D曲线为Q=6000−20p,其中Q是行业的年产量[似应为对行业产品的总需求量].问:4.1.该行业的长期均衡产量和(4.2问)有多少家企业.解:竞争意味着长期边际成本等于价格,即LMC−p=0JSj()j()D()Q=∑qp=Jqp=Qp行业的长期均衡意味着供求相等,即j=1[上标s表示供给;所有企业都是完全相同的,均衡中供给量也会相同],同时经济利润为零,即(j)jLMCq=pq.将这三个方程式联立,有69
第八讲完全竞争与垄断2⎧0.3q−2.4q+111−p=0⎪⎨Jq=6000−20p⎪32⎩0.1q−1.2q+111q=pqqe,pe=107.4,e=642可以解得:=6J.长期均衡中行业产出量为eeeQ=Jq=3852.[另外一个列方程式的办法是将第一和第三个方程联合起来,它们等价于平均成本等于边际成本的长期竞争均衡条件.]4.2.若政府决定将该行业的企业个数减至60家,并且用竞争性投标的方法每年出售65份许可证.于是企业的数目固定为60家,并且这60家企业的竞争性经营将形成新的均衡,那么产品的新价格是多少?一份一年期许可证的竞争均衡价格是多少?解:[这里按照完全市场均衡的前提解.也有认为应当用古诺均衡解,我这样解是基于(1)本讲尚未涉及古诺均衡,以及(2)完全竞争由“如果一个市场中每家厂商都认为市场价格与自身产量大小无关,那么这个市场就是纯粹竞争市场”(范里安)来定义以及在他书(中文1994版)上举的鱼市的例子,这两个理由]令上题的J=60,且将经济利润等于许可证价格R条件,则有方程组:2⎧0.3q−2.4q+111=p⎪⎨60q=6000−20p⎪32⎩pq−()0.1q−1.2q+111q=Rrr可以解得,q≈49.24,p≈152.28,r表示政府的管制.均衡许可证价格R≈3934.8.TC=8+20(q+q)5.设某完全垄断企业的总成本函数为ab,其产品分别在A、B两个市p=100−qp=120−2q场销售.若两市场的需求函数分别为aa,bb.试求A、B两市场的价格、销售量、需求价格弹性及企业利润.解:根据边际成本等于边际收益,得到MC()q=MR(q)aa,MC()q=MR(q)bb.q=40q=25解方程,得到a,b.pdqaaε==1.5a相应地得到价格,pa=60,pb=70.需求价格弹性qadpa,70
第八讲完全竞争与垄断pdqbbε==1.4bqdpbb.2TC=q+,6.设某完全垄断企业拥有A、B两个工场,成本函数分别为A4A52TC=2q+10.市场需求函数为p=100−2Q.BB6.1.求该企业利润最大的产量,价格和利润.MR()Q=100−4QMC(q)=MC(q)=MR(Q),有方程组解:,令AB8q=100−4()q+q,4q=100−4(q+q)AABBAB解得qA=5,qB=10.因此利润最大的产量为15,价格为70,利润为735.6.2.若政府采用边际成本定价法对其产品价格加以限制,则该企业的产量、价格、利润为多少?这时,政府宜采取何种辅助措施.50100q=q=MC(q)(=MCq)=100−2(q+q),有A7B解:令ABAB,7.价格为4007,利润约为597.这时,政府应当补贴边际成本定价法与垄断定价法的利润差额,为238.7.判断对错并说明理由7.1.在长期竞争性均衡中厂商的利润为零,所以在竞争性行业的财务报告中部应看到普遍的正的利润.答:错.财务报告中的利润包括了经济利润和企业自身拥有的资本带来的收入,在竞争性企业长期均衡中,经济利润为零,这种普遍为正的利润是企业自身拥有的资本收入.7.2.如果市场需求曲线向下倾斜,则每个厂商面对的需求曲线也向下倾斜.答:经济理论中允许无穷数量的厂商存在,在该情况下,向下倾斜的需求曲线也不会意味着一个厂商可以单独影响价格,即需求曲线水平.在实践中,竞争性行业中单独厂商规模如果足够小,其足够小的一个产出变化不会影响市场价格;这时也可以认为它的需求曲线是水平.7.3.垄断厂商的供给曲线是向上倾斜的.答:无意义的命题.供给曲线是厂商作为价格接受者时,它利润最大化的产出与价格的关系.因此垄断厂商无所谓供给曲线.[注:它的供给水平由边际成本等于边际收益决定,即使在同一个价格水平,也会因为需求曲线弹性的不同而供给量不同.]7.4.垄断企业有可能在需求曲线的任何点选择生产.答:由Leanerindex知,如果需求曲线存在弹性小于1的地方,垄断企业就不可能在该点生产.7.5.如果利率为10%,垄断者将会选择在边际成本基础上加价10%.答:利率决定了资本利用的边际成本,但是[据我所知]与需求曲线弹性的变动在理论71
第八讲完全竞争与垄断上没有已知的确定关系.8.已知汽油市场上的供求如下DS需求:Q=150−50pD,供给:Q=60+40pS.求8.1.市场上的均衡价格与数量.DSee解:令Q=Q,pD=pS.解得,p=1,Q=100.上标e表示均衡.8.2.此时若政府对每单位产品征收0.5单位的税收,求此时的市场价格与数量.e11e800DSppp=pD=Q=解:令Q=Q,D=S+0.5.解得,9,9.8.3.求解消费者剩余与生产者剩余的损失,与政府所得比较,社会存在净损失么?1D()∆CS=∫11QpDdpD≈−21.0解:消费者剩余的变化9,生产者剩余的变化13()S∆PS=18pQdp≈−26.2∫1SS,∆SW=∆CS+∆PS=−47.2,而政府所得800∆T=0.5×≈44.49.因此有社会福利变化∆SW=∆CS+∆PS+∆T=−2.8.所以,社会存在净损失.9.假设你作为中国电信的经理正在决策北京和石家庄固定电话的定价问题,已知需求函数为石家庄:p1=a−Q1北京:p2=b−Q2C(Q)=cQ(cR,a−b1()2p=+cA=3b−a−2c那么最佳策略就是2,8.如果π10,但π13c时,a−ca−c≤b02()其一阶条件为−3x+2x−C′x=0.若垄断电信公司实现100%的电话普及率,即x=1,一阶条件为−1−C′()1=0.又C′()x>0,所以一阶条件不成立.所以,垄断公司不可能实现100%的普及率.79
第九讲Cournot均衡,Bertrand……第九讲Cournot均衡、Bertrand均衡与不完全竞争1.考虑一个由两家企业组成的寡头垄断行业,市场的需求由p=10−Q给出.两家企业的成本函数分别为C1=4+2Q1,C2=3+3Q2.1.1.若两家串通追求共同的利润最大化总的产量水平是多少?市场价格多大?各自生产多少?各自利润多大?解:两家串通追求共同的利润最大化,有maxQ[10−Q]−(C+C)12Q1≥0,Q2≥0解得,Q1=4,Q2=0****Q=,市场价格为p=6.Q=4,Q=0;1的利即,利润最大化的产量水平412润为12,2的利润为零.1.2.若两家追求各自的利润最大化,利用古诺模型,各自生产多少?各自利润多大?市场价格多大?并给出各自的反应函数.解:给定企业2的产量Q2,企业一的反应函数由maxQ1[10−(Q1+Q2)]−C1Q1≥0的一阶条件决定,为Q2Q=4−12同理,可得企业二的反应函数Q1Q=3.5−22CC古诺均衡意味着Qi=Qi,i=1,2.可以得到古诺均衡为Q1=3,Q2=2.市场价格为5,利润两家分别为5和1.()Q,Q注:从任何一个12的组合开始,通过相继进行的产量决策,都会得到该均衡结果.1.3.若串通是非法的,但收购不违法.企业1会出多少钱收购企业2?解:至多为7.2.一个垄断企业的平均成本和边际成本为AC=MC=5,市场的需求曲线为80
第九讲Cournot均衡,Bertrand……Q=53−p.2.1.计算这个垄断企业利润最大化时的产量和市场价格,以及其最大化的利润.解:记该垄断企业的产出为q1,有Q=q1,则市场的边际收益MR=53−2q.令MR=MC=5,得q1=24.因此垄断利润最大化的产量为24,价格为29,利润为576.2.2.若又有第二个企业加入该市场,市场的需求不变.第二个企业生产成本和第一个相同,在古诺模型下,求各企业的反应曲线、市场价格、各企业的产量和利润.q解:记第二个企业的产出为2.对厂商一,它的反应函数由利润最大化问题maxq(53−q−q)−5q1121q1≥0qq21q=24−q=24−12的一阶条件2决定,同理可以得到厂商2的反应函数2.古诺CC均衡意味着qi=qi,i=1,2.解得q1=q2=16,市场价格为21,两个企业的利润均为256.2.3.若有N个企业加入该市场,市场的需求不变.这N个企业生产成本和第一个相同,在古诺模型下,求市场价格,各企业的产量和利润.q解:记第i个企业的产出为i;它的反应函数由利润最大化问题⎛⎞maxqi⎜⎜53−qi−∑qj⎟⎟−5qiqi≥0⎝j≠i⎠1qi=24−∑qj的一阶条件2j≠i,i=1,2,...,N.N−1Q=24N−Q加总所有企业的反应函数,并注意Q=∑qi,得到2.古诺均衡C48NQ=意味着Q=Q,解出N+1.C1C48q=24−∑qqC=48−QC=ij2i又由在均衡下j≠i,可得在均衡下N+1.25N+53⎛48⎞⎜⎟市场价格为N+1,单个企业利润为⎝N+1⎠.81
第九讲Cournot均衡,Bertrand……注:这个问题的很多解法,均依赖一个概念叫“对称均衡”[我没有发现它的定义];但是,至少对该问题,事实上是不需要这个概念作为支撑的.2.4.当N趋于很大时,市场价格有什么变化趋势?C5+53Nlimp=lim=5pC(N)N→∞N→∞1+1N解:记N个企业的古诺均衡价格为,则有,接近完全竞争市场价格.311/2−1/2S=p3.在世界石油市场上,石油的需求W=160p,非欧佩克的供给为3,欧佩克的净需求为D=W−S.3.1.试画出世界石油市场上石油的需求曲线,非欧佩克的供给曲线和欧佩克的需求曲线,为简单起见,设欧佩克的生产成本为零.在图中指出欧佩克的最优价格、欧佩克的最优产量,以及非欧佩克的产量.解:pSpopecWDSopec−1/2311/2D=160p−p由3,可以令欧佩克的边际收益等于边际成本,即−1/2311/216080p−p=0p=MR(popec)=MC(popec)opec2opecopec,有,得到31,其产量S=47.17opec,非欧佩克的产量S=23.46.3.2.若非欧佩克国家石油储量资源开始枯竭,生产成本开始上升,各条曲线会如何移动?答:以价格为纵坐标,非欧佩克国家供给曲线左移,欧佩克面临的需求曲线左移,世界需求曲线不变.3.3.若石油消费国联合起来,形成买方垄断势力,这会对世界石油价格造成怎样的冲击?答:[我能得到的结果]油价非增.原来的竞争是欧佩克领导价格的模型,但是,在买方垄断形成后,则可以通过谈判来确定油价;而很明显,谈判时买方的底线明显是买方处于价格接受者时的价格.所以可以预见油价非增.82
第九讲Cournot均衡,Bertrand……4.一个生产榴莲的卡特尔由四个果园组成.它们的总成本函数分别为2TC=20+5Q112TC=25+3Q222TC=15+4Q132TC=20+6Q444.1.用列表的形式列出产量在1到5之间各果园的总成本、平均成本、边际成本.ACMC解:记i为i的平均成本,i为i的边际成本,i=1,2,3,4.qi12345TCi25|28|19|2640|37|31|4465|52|51|74100|73|79|116145|100|115|170MCi5|3|4|615|11|12|1825|15|20|3035|21|28|4245|27|36|54ACi25|28|19|2620|18.5|15.5|2232.5|26|25.5|3750|36.5|39.5|5872.5|50|57.5|85每一项从左到右分别是第1、2、3、4个果园的对应值.4.2.如果该卡特尔将总产量控制为10,而价格定为25,产量在各果园之间应怎样分配?解:从第一个的列表里,找出各个边际成本里最小的十个值,在上面我标成了黑体字,结论是,第1,4个果园分别生产2,另外两个分别生产3.4.3.在4.2的产量水平和价格下,是否每个果园都没有欺诈的激励?若有,哪个果园欺诈的激励最大?解:只有两个果园有欺诈的非负激励,分别是第1个和第2个,它们的数字被打成斜体.其它两个都高过价格25,它们的价格被打了下划线.第1个果园多生产一个的边际成本为25,刚好和价格水平相同;第2个果园多生产一个的边际成本为21,比价格水平低4;所以第二个果园背叛的激励是最大的.5.假定有n家相同的厂商处于古诺均衡情况下,求证市场需求曲线弹性一定大于1/n.证明:设厂商i的成本函数为C(qi),市场需求反函数为p=p()Q,其中Q=∑qi.给定qj,j≠i,厂商i的问题是maxp()Qq−C(q)iiqip′()⋅q+p(⋅)−MC(q)=0其一阶条件为ii,是为其反应函数.q[注:由于所有厂商相同,因为该处i不会等于零.这里只能这样说.应该有严格的证明.不过这点不影响结果.]83
第九讲Cournot均衡,Bertrand……加总所有厂商的反应函数,并利用Q=∑qi,以及均衡时,qi=qi,有:p′Q+np−∑MC(q)=0i两边同除以p,整理得到:dQp11ε==>dpQ∑MC()qinn−pMC(q)i<1注:p6.(价格竞争模型)有两个寡头企业,它们的利润函数分别是:()222π=−p−ap+c+p[原文此处为p,怀疑有误]1122()2π=−p−b+p221其中,p1,p2分别是两个企业采取的价格,a、b、c为常数.6.1.求企业1先决策时的均衡.6.2.求企业2先决策时的均衡.解:由霍太林引理得到两个寡头企业给定对方价格的反应函数:p()p=ap−c122p()p=b21企业1先决策情况:根据企业2的反应函数,得到p2=b,代入1的反应函数,得到p1=ab−c.因此,()p,p=(ab−c,b)企业1先决策的均衡是12(p,p)=(ab−c,b).企业2先决策情况,其均衡也是126.3.是否存在某些参数值,使得每个企业都希望自己先决策.答:否.7.对某商品,市场需求曲线为p=100−2Q,生产该产品的任何厂商的总成本函数都为TC()q=4q.7.1.假设市场上有两个古诺厂商A、B,这两个厂商的反应线分别是什么?求解古诺均衡时的产量.解:记A、B的产出分别为qA、qB.给定qB=qB,A的问题是84
第九讲Cournot均衡,Bertrand……maxq()100−2Q−4qAAqA从一阶条件可以得到A的反应线:qA=48−0.5qB同理,B的反应线是qB=48−0.5qAcc古诺均衡意味着qi=qi,i=A,B,这样可以得到古诺均衡(qA,qB)=()32,32.7.2.假设市场上由两个厂商,一个是领导者A,一个是追随者B,求解Stackelberg均衡时的产量.解:因为B决策时,qA已知,所以B的反应函数为qB=48−0.5qA,代入A的最大化问题中,有maxq()100−q−(48−0.5q)−4qAAAAqA由一阶条件解得:qA=48(ss)()q,q=48,24.再将qA=48代入B的反应函数,由此可得Stackelberg均衡为AB8.考虑一个新开发的市场,该市场每年的需求为Q=10−p.在第一期企业1抢先进入,并以广告的方式进行大量宣传.在它正要进行生产时得知企业2正在订购生产此产品的()2CQ=Q.已知企业1的成本函数为设备,并通过调查得知企业2的成本函数为222C()Q=4+2Q.1118.1.如果你是厂商1,你将抢先向社会宣布什么样的生产计划(即产量为多少),这时厂商2会宣布生产多少?解:Stackelberg竞争已知Q1,厂商2的最大化问题是()2maxQ10−Q−Q22Q2由一阶条件得到反应函数Q2=2.5−0.25Q1将该函数代入厂商1的最大化问题中,有maxQ()10−Q−(2.5−0.25Q)−(4+2Q)1111Q1由一阶条件得厂商1宣布的产量85
第九讲Cournot均衡,Bertrand……11Q=1319Q=2代入厂商2的反应函数,得到厂商2宣布的产量12.8.2.在第二年初出于行业的惯例,两厂商同时发布产量,这是你预计产量会有变化么?解:古诺竞争问题.令Q2=Q2,有厂商1的最大化问题maxQ()10−Q−(4+2Q)11Q1由一阶条件得厂商1的反应函数Q1=4−0.5Q2令Q1=Q1,由8.1的解答得厂商2的反应函数Q2=2.5−0.25Q1.cc⎛2212⎞()Q1,Q2=⎜,⎟令Q1=Q1,Q2=Q2,得到古诺均衡⎝77⎠9.下列说法对吗?请说明理由在垄断竞争行业中,价格竞争的结果可能是Bertrand均衡.答:错.Bertrand均衡存在的必要条件之一是商品同质.而垄断竞争存在的必要条件之一就是产品异质.10.考虑一个垄断竞争市场,其中有101家企业.每家企业所面临的市场需求与各自的成本函数都是相同的pk=150−qk−0.02∑qj32j≠k,Ck=0.5qk−20qk+270qk,k=1,2,...,101请确定该市场中代表性的企业(每一家企业的行为都是相同的)的最大利润价格与产量水平.(假定行业中的企业个数不发生变化)解:代表性企业的最大化问题是⎛⎞maxqk⎜⎜150−qk−0.02∑qj⎟⎟−Ckqk⎝j≠k⎠一阶条件为2−1.5qk+38qk−0.02∑qj−120=0j≠kq=q由于每一家行为均相同,有ij,i≠j,上式为2−1.5q+36q−120=0kkq=20解得,k或4(舍去).即,代表性企业的最大利润产量为20,价格为30.q=4注:舍去k,可以通过最大化的二阶条件来验证.11.某一市场需求函数如下86
第九讲Cournot均衡,Bertrand……p=100−0.5(q+q)12在该市场上只有两家企业,它们各自的成本函数为2c=0.5qc1=5q1,2211.1.在斯塔克博格模型中,谁会成为领导者?谁会成为追随者?11.2.该市场最后的结局是什么?为什么?解Stackelberg模型,可参考一下8.1,这里我懒了,主要是要说一下逻辑上的问题.这道题有不同解答.一个可以参考的是,中心考过.中心参考答案的逻辑是这样,对于第1问,假如说企业A领先的情况下,企业B能在自身利润非负的条件下使得企业A的利润为负,企业A就不会成为领导者.这个答案的逻辑在于将这个博弈看作广延博弈.第二个问题中心的解答基于Stackelberg均衡中领先者的利润大于它古诺均衡下的利润.因此,两个企业都希望能当第一,当然结论就是同时出手,古诺均衡.考虑一次博弈则得到这个结论.广延博弈中也可能得到这个结论.也就是说,两个问题的解答,一是有附加条件;二是,加上这些假设,也不见得自洽.我相信需要放在广延博弈的背景下才能看出谁能成为领导者.第二个问题的古诺解,则可以通过重复交互定价的过程得到.12.设一市场上只有两个生产者.产品稍有差别,但仍可以相互替代.寡头1所面临的市场2c=2.5q.假定寡头2只想维持逆需求函数为p1=100−2q1−q2,其成本函数为111/3的市场份额.求:q1,q2,p1与π1.解:由“寡头2只想维持1/3的市场份额”知,q2=0.5q1.因此寡头1所面临的市场为需求为p1=100−2.5q1.寡头1的最大化问题为()2maxq100−2.5q−2.5q111q1由一阶条件,求得q1=10.因此,q2=5,p1=75,π1=500.13.考虑一个两期的垄断者问题.在第1期与第2期,市场需求函数都是q=1−p.在时期1中,单位成本为c;在时期2中,单位成本为c−2λ.时期之间的贴现因子为1,记q1为时期1的产量.87
第九讲Cournot均衡,Bertrand……1−cq=1求证:2−λ[两个时期的成本不同,为什么?一种解释是,两时期的产品在耐用度上是不一样的.时期1卖的产品要用完两个时期,禁得用,就要多费工.这个思路来自平老师产业组织的讲义,第1章]证明:市场反需求函数为p=1−q.r消费者可以选择第1时期买,也可以选择第2时期买;如果一个消费者的保留价格为x,2(r−p)那么他在第一时期买的消费者剩余为x1,第二时期买的消费者剩余为rx−p2.这意味着,在价格组合(p1,p2)满足一定的条件时,存在一个消费者在第一2(r−p)=r−p时期和第二时期购买是无差异的,他的保留价格由x1x2确定,即为rx=2p1−p2.这里先假定2p1−p2∈(0,1).很明显,保留价格高于他的人愿意在第一时期购买,保留价格低于他的人愿意在第二时期购买.再考虑厂商的决策.第二阶段,厂商的问题是max[]p−(c−2λ)(1−p−p)212p2得到p=0.5()−p+c−2λ+1.21于是,第一期的需求就是q=1−r(p,p)=−2.5p+0.5(c−2λ)+1.51x121其最大化问题为max[]p−c(−2.5p+0.5(c−2λ)+1.5)11p2一阶条件可以解到p1=0.6c−0.2λ+0.313(《十八讲》第2版)考虑一个两期的垄断者问题.在第1期与第2期,市场需求函数都是q=1−p.在时期1中,单位成本为c;在时期2中,单位成本为c−q1λ.时期之间的贴现因子为1,记q1为时期1的产量.1−cq=1求证:2−λ证明:记两期利润分别为π1、π2,又贴现因子为1,所以垄断者的利润为π=π1+π2.88
第九讲Cournot均衡,Bertrand……因此厂家的利润最大化问题为max[]q()1−q+q(1−q)−cq−(c−qλ)q1122112q1,q2一阶条件为−2q1+λq2+1−c=0λq1−2q2+1−c=01−cq=1由此,可以解得2−λ.注:此解答来自billqian的“十八讲个人意见.rtf”,来自gsmer.net.解答过程有所不同.第二版的这个题目大概是“正确”的版本,毕竟解答不是太麻烦.q1进入第二期的成本函数可以看成学习效应.14测度厂商分布的一个方法是使用荷凡达尔指数,定义为2H=∑αiα这里i是厂商i在总行业收益中的份额.证明,如果行业中所有厂商有不变规模收益的生产函数且遵循古诺产出决策,总行业利润对总收益的比等于荷凡达尔指数除以需求的价格弹性.这一结果意味着行业集中与行业盈利有什么样的关系?c(q)=cq解:设有N家相同的厂商.记厂商i的成本函数为ii,c>0.记行业的需求函数为p=p()Q,Q=∑qi.从第5题的解答,在古诺均衡中p′Q+N()p−c=0q=q均衡中,i,i=1,2,L,N,则有Q=Nq,带入上式有单个厂商的产出决定式p′q+()p−c=0()22单个厂家利润是p−cq=−p′q,收益为pq,总行业利润Π=−Np′q,总收益R=Npq.2Π−Np′qp′q==−RNpqp.211H=∑αi=N⋅2=因为所有厂商都相同,所以NN.89
第九讲Cournot均衡,Bertrand……Πp′Q111H=−==综上,RpNNεε.注:周惠中的书上有一个在更一般条件下的证明.15在克罗若克斯(Clorox)案例中,宝洁公司推断一个潜在的进入者要进入洗涤液市场.你是否可以设计一个运用厂商的成本曲线与厂商所面对的需求曲线的方法,用来区别真正的进入者、潜在的进入者与没有进入者时的情况?运用你的分析说明在这一反托拉斯的案例中,法庭应该寻找什么?答:该案例是美国六十年代的一个反托拉斯案例FederalTradeCommissionvs.Procter&Gambler.当时Clorox在该市场占有70%的市场份额.当时宝洁想收购该公司以进入此市场.最后最高法院阻止了收购,理由是,宝洁是该市场唯一没有进入、且有强劲实力进入的厂商,它的存在已经能使Clorox的行为保持一定的竞争性;因此一旦收购成功,该产业的集中程度将升高,并且垄断性更强(尽管宝洁声称从未打算自己进入该市场).从这个角度来说,原题中的“推断”应当是翻译错了.从我在网上找到的资料,“真正的进入者、潜在的进入者”很大可能译自“actualpotentialentrant(APE)”,是一个概念翻译成了两个概念.该案的关键是确定宝洁是否在未进入该市场时仍能对Clorox保持“压力”.一个APE需要满足的条件是,该厂商是有经济动机自己进入该市场的,而它不进入市场,也会使市场的在位者(incumbent)保持寡头垄断行为.从洗涤剂生产的成本曲线,和洗涤剂Clorox之外市场剩余需求出发,如果能够发现在Clorox保持垄断定价水平时,宝洁进入该市场,面临剩余需求而仍然能保持利润为正的生产,那么宝洁就是一个actualpotentialcompetitor.因为,有这样的进入可能,必然使Clorox保持寡头竞争的一些行为,比如说产量大于垄断产量等.最后,该题目考察的实际上是一个价格或产量领导模型,如果Clorox在价格或产量领导的条件下,宝洁自身进入后,可以保持利润非负,那么宝洁就是一个APE.回到法庭应该寻找的证据,Clorox和洗涤剂产业当前的边际成本、价格水平、销售量和需求弹性,以及进入产业的固定资本投资都是可观察到的变量.利用这四个变量可以粗略计算出Clorox是否具有寡头竞争的行为,由于宝洁很明显是唯一可能对该市场形成压力的对手(宝洁太强了),由此可推断宝洁是否是APE.注:参考了http://law.cwru.edu/student_life/journals/law_review/52-1/KWOKA.PDF上对APE等相关概念的定义和该案例相关内容.16在一个中等城市中,电话的需求为Q=1000−50p这里Q是家庭安装电话的数量(单位:千门),p是使用电话的每月租金(单位:美元).电话系统得成本由下式给出TC=500ln(0.1Q−20)对于Q>20016.1本城市的电信业务是否是一个自然垄断的行业?500MC=解:电信业务的边际成本Q−200,因为MCQ′<0,平均成本随产出增大而减少,因此他是自然垄断.90
第九讲Cournot均衡,Bertrand……16.2在这种情况下,什么样的产出水平将产生一个无管制的垄断?消费者要支付的价格是多少?垄断利润是多少?1MR=20−Q解:25.令MC=MR,得到Q=450,或Q=250(舍去,因为二阶条件不符合最大化).因此,450千台的产出水平将产生垄断,消费者的价格为11,垄断利润约为3341.16.3如果允许活跃的竞争,价格会有什么变化?解:自然垄断条件下,他人无法以非负利润进入市场.但是,可以通过购买该公司进入.综上在竞争条件下,价格没有变化.(但厂商的经济利润为零.)cyy17假定平板玻璃市场有j个厂商,它们的成本函数都是j,其中j代表第j个厂商的产量,c为正的常数.市场的反需求函数p(y)是递减函数.17.1如果该市场完全竞争,那么市场价格、每个企业的销售量和利润额将是多少?1q()c答:市场价格将是c,销售量为j,利润额为零.17.2这个行业里的厂商认为低价倾销使它们的利润受损失,于是成立行业协会规定最低限价,那么将由什么原则决定各自的产量定额和自律价标准?它们各自的利润较前有多大变化?mc−pq=c=p+p′qp′答:垄断定价.令MC=MR,即q,来确定总产量q.各mmqqπ=()p−c(m)自产量为j,自律价为pq,各自利润从零增加到j.17.3这种合谋定价,如果没有政府支持,可能长久么?为什么?(用数学公式表述)p−cπ′=π′=>0qjq答:不可能.因为j,所以任何一家厂商都有动力提高产量水平.17.4从社会经济效率的角度看,政府是否应该帮助此行业实行价格“自律”?为什么?(用图形或数学公式表达)dswq=p()q−csw=∫()p()y−cdydq答:不应该.社会的福利为0,非负,只要mmp>0,由于p(q)>c,又p(y)单减,所以q(c)>q.综上,(m)()()swq1且c<1,(2)c<1且b<1,(3)b<1且c0clti,i.因此,满足以上条件的策略组合(a,b),都是该博弈的混合策略纳什均衡.7巧克力市场上有两个厂商,各自都可以选择取市场的高端(高质量),还是去低端(低质量).相应的利润由如下得益矩阵给出.厂商2低高厂商1低-20,-30900,600高100,80050,507.1如果有的话,哪些结果是纳什均衡.答:(高,低),(低,高),对应结果分别为(100,800),(900,600).7.2如何各企业的经营者都是保守的,并都采用最大最小化策略,结果如何?答:均衡为(高,高),结果为(50,50).7.3合作的结果是什么?答:均衡为(低,高),结果为(900,600).7.4哪个厂商从合作的结果中得好处最多?那个厂商要说服另一个厂商需要给另一个厂商多少好处?答:厂商1得好处最多.应该给200.[这个问根据不同的标准,应有不同的答案.]8考虑在c,f,g,三个主要汽车生产商之间的博弈.每一个厂商可以生产要么打大型车,要么小型车,但不可同时生产两种型号的车.即,对于每一个厂商i,i=c,f,g,他95
第十讲策略性博弈与……AI={}SM,LG.用iiIΠIac,af,ag的行动集合为a代表i所选择的行动,a∈A,()代表厂商i的利润.假设,每个厂商的利润函数定义如下:πi≡γj,如果a=LG,j=c,f,g;jγ,如果a=SM,j=c,f,g;ijα,如果a=LG,且a=SM,j≠i;ijα,如果a=SM,且a=LG,j≠i;ijkβ,如果a=a=LG,且a=SM,j≠k≠i;ijkβ,如果a=a=SM,且a=LG,j≠k≠i.8.1当α>β>γ>0时,是否存在纳什均衡,请证明.(ijk)()答:存在纳什均衡.纳什均衡是a,a,a=SM,SM,LG,(LG,LG,SM).考虑三家选择行动相同,那么任何人得到γ,又α>β>γ,所以任何厂商都有动力背(ijk)()离自身选择.当三家选择行动不同时,不妨考虑a,a,a=SM,SM,LG,给定其他人的选择i没有动力背离,因为α>γ,而给定其他人的选择,j、k对背离与否是无差异的,因此该策略组合是一个纳什均衡.8.2当α>γ>β>0时,是否存在纳什均衡,请证明.答:存在纳什均衡.如果三家行动相同,那么给定其他人的选择,任何一个人都有动(ijk)()力背离,因为α>γ.如果三家行动不同,考虑a,a,a=SM,SM,LG,k没有动力背离,因为α>β,而给定其他人的选择,i、j对背离与否是无差异的,因此,该策略组合是一个纳什均衡.9考虑下列策略性博弈:BLMRU1,-2-2,10,0AM-2,11,-20,0D0,00,01,196
第十讲策略性博弈与……请问,该博弈里有几个均衡?为什么?答:只有一个均衡,即纯策略均衡(D,R).考虑混合策略均衡,设B选择L、M、R的概率分别为a、b、c,使A对各个纯策略无差异,它们需要满足a+b+c=1,a−2b=−2a+b=c,且1≥a,b,c≥0但由前两个条件解得唯一解a=b=1,c=−1,但该解不满足最后一个不等式条件.所以该博弈不存在混合策略纳什均衡.10考虑下列策略型博弈:A2LR1U0,0,10-5,-5,0D-5,-5,01,1,5B2LR1U-2,-2,0-5,-5,0D-5,-5,0-1,-1,5每一格左边的数字是游戏者1的得益,中间的数字为游戏者2的得益,右边的数字为游戏者三的得益.游戏者三的策略是选择A矩阵或选B矩阵.10.1上述博弈中有几个纯策略纳什均衡?为什么?答:有两个,(U,L,A)和()D,R,A、(D,R,B).在矩阵中,对任意行动者,将给定其它两个游戏者的行动,他的占优行动用下划线表示出来;由此可以得到这三个纯策略纳什均衡.10.2如果三个游戏者中可以有两个人结盟共同对付另一个人,会出现什么结果.在哪一个均衡结果中没有人会有“结盟”动机?为什么?答:在均衡中,当存在一个策略的同时改变,使得“同盟”中成员的收益非减.那么,我认为这样的同盟是可能的.在均衡()U,L,A中,3没有动力与任何人结盟以改变,因为它在该均衡中得到了最高payoff,10.给定3选择A,1和2有动力结盟,同时改变选择,以到达均衡()D,R,A,使双方的收益增加1.在均衡()D,R,B中,给定3的选择B,1和2没有结盟动力.而给定1或2的选择,2或1都可以与3结盟,以到达均衡(D,R,A),使得2或1的收益增加2,而3的收97
第十讲策略性博弈与……益不变.由于在三个纯策略均衡中,以上两个均衡中所形成的同盟,其转移目标均为均衡()D,R,A,所以在()D,R,A,没有同盟可以存在.11在下列策略型博弈里,什么是占优解?什么是纯策略纳什均衡解?IILMRT2,01,14,2IM3,41,22,3D1,30,23,0没有占优解.纯策略纳什均衡解为(M,L),(T,R).12判断对错,并简要说明理由.12.1如果每个人的策略都是优超策略,那么必将构成一个纳什均衡.答:对.因为在优超策略组合中,给定其他人的策略,每个人都没有动力改变自己的选择.12.2在囚徒困境中,如果每一个囚犯都相信另一个囚犯会抵赖,那么两个人都会抵赖.答:错.因为每一个囚犯都不知道对方知道自己会抵赖,以此类推.12.3一个将军有两个纯策略,要么把所有的部队从陆地运输,要么把所有的部队从海洋上运输.那么把1/4的部队从陆地运输,把其余3/4的部队从海洋运输构成一个混合策略.答:错.这仍然是一个纯策略.混合策略是在纯策略集合上确定的一个概率分布.而该题中,将军分割军队的决定事实上是扩大纯策略的集合.13一个小镇中,有N个人,每人有100元钱,如果每人都向一个集资箱中捐一笔钱(可以为零)而共收集到F元,那么从一个基金中拿出相同数量的钱放入集资箱,最后当集资被分配时,每人获得2FN元,求解这一博弈的均衡.ii答:考虑行动者i,1≤i≤N.记i捐出的钱为F,i的收益为π,又记i2(i−i)iπ=F+F−F−ii−i−iF=F−F.给定F=F,N,最大化收益的一阶条件iidπdπ2≤0=−1iii为dF,且在F≠0,等号成立.又dFN.所以idπ<0ii当N>2时,dF,所以F=0.98
第十讲策略性博弈与……idπ≡0i当N=2时,dFi,所以F∈[0,+∞).idπ>0ii当N=1时,dF,所以F→+∞.i由于所有行动者的行为相同,所以当N>2时,纳什均衡为F=0,i=1,2,...,N.当Fi,i=1,2.当N=1时,纳什均衡为i→+∞N=2时,纳什均衡为∈[0,+∞)F.14Frank和Nancy约定下一周的某一天在小镇的咖啡厅见面,但他们如此兴奋以至于忘记了在哪一个咖啡厅约会,所幸得是小镇上只有两个咖啡厅,“夕阳”和“海湾”,并且他们知道彼此的偏好.事实上,如果二人都去了“夕阳”,Frank的效用是3而Nancy的效用是2,如果二人都去了“海湾”,Frank的效用是2而Nancy的效用是3,如果而然去的地方不同,则效用水平都是0.14.1这一博弈存在纯策略纳什均衡吗?存在混合均衡吗?答:纯策略纳什均衡为二人都去“夕阳”,二人都去“海湾”.以下求混合均衡.令p为Frank去“夕阳”的概率,那么让Nancy对去“夕阳”或“海湾”无差异的p值需要满足2p=3()1−p,得到p=0.6.令q为Nancy去“夕阳”的概率,那么让Frank对去“夕阳”或“海湾”无差异的q值需要满足3q=2()1−q,得到q=0.4.因此,混合均衡为()()0.6,0.4,(0.4,0.6).14.2这一博弈存在占优策略均衡吗?答:不存在.99
第十一讲广延性博弈……第十一讲广延型博弈与反向归纳策略1考虑下图所示的房地产开发博弈的广延型表述开发商A(开发)(不开发)开发商B开发商B(开发)(不开发)(开发)(不开发)()−3,−3(1,0)(0,1)(0,0)1.1写出这个博弈的策略式表述.A开发不开发B开发()−3,−3(1,0)不开发(0,1)(0,0)1.2求出纯策略纳什均衡.在策略式表述的收益矩阵里,将给定对方策略,本方占优策略所对应收益以下划线表示.由此可得该博弈的纯策略纳什均衡为(开发,不开发),(不开发,开发).1.3求出子博弈完美纳什均衡.用反向归纳法.当A选择开发,B将选择不开发,因为这样B的收益0大于开发的收益−3,这样A选择开发的收益为1.同理可得A选择不开发收益为0.因此,A会选择开发.(用箭头表示在给定结点行动者的最优策略.)可得到子博弈纳什均衡(开发,不开发).2你是一个同质产品的双寡头厂商之一,你和你的竞争者生产的边际成本都是零.而市场的需求为p=30−Q2.1设你们只有一次博弈,而且必须同时宣布产量,你会生产多少?你期望的利润时多少?为什么?答:我的产量为古诺解.解古诺均衡得到,q=10,利润为100.因为,一次产量竞争,各方均按照预期对方产量来确定利润最大化产量,在均衡中意味着预期与实际产100
第十一讲广延性博弈……量相等.所以预期产量应为古诺均衡解.2.2若你必须先宣布你的产量,你会生产多少?你认为你的竞争者会生产多少?你预计你的利润是多少?先宣布是一种优势还是劣势?为了得到先宣布或后宣布的选择权,你愿意付出多少?答:先宣布产量等同于在Stackelberg竞争中作为领先者.这时,我的最优产量为15,预期利润为112.5.而此时对方产量为7.5,预期利润为56.25.与同时宣布和后宣布相比,先宣布为一种优势.[与古诺解相比,这只是一种角度.]我愿意付出12.5.2.3现在假设你正和同一个对手进行十次系列博弈中的第一次,每次都同时宣布产量,你想要你十次利润的总和(不考虑贴现)最大化,在第一次你将生产多少?你期望第十次生产多少?第九次呢?为什么?答:第一次仍将生产10,而第十次,第九次仍然生产10.按反向归纳法,考虑第十次博弈,子博弈纳什均衡要求该次博弈必然为纳什均衡,即古诺均衡.由于第九次博弈的结果对第十次没有影响,因此第九次的均衡也是古诺均衡.[同理可得在十次博弈中任一次的均衡皆古诺均衡.]3考虑下列三个广延型博弈,哪一个博弈有多重反向归纳策略.答:a的子博弈纳什均衡有两个,((L,L′′),L′),((R,R′′),R′).b的是(O,(L′,L′)),其中O是指向结果(2,0)的行动.c的是((L′,R′),L),((L′,R′),R).但我不知“多重”是什么意思.注:说明一下,比如策略((R,L′′),L′).外面括号表示这是一个策略组合,该括号内按先写1的策略,再写2的策略.1的策略包括两个结点上的行动,因此用括号包101
第十一讲广延性博弈……括起来.这两个行动按在博弈树上离初始结点的“距离”近远来排列先后次序,如果“距离”相等,则按结点在具体图中的左右位置排列,如b博弈中2的策略.若无特殊说明,以后均按此例.4请将下列广延型博弈转化为策略型博弈,并求纳什均衡.解:该博弈转化为策略型博弈为1LR2l1,30,0r0,03,1其纳什均衡为(L,l),()R,r.5两家电视台竞争周末黄金时段晚8点到10点的收视率.可选择把较好的节目放在前面还是后面.他们决策的不同组合导致收视率如下:电视台1前面后面电视台2前面18,1823,20后面4,2316,16[我怀疑该题目有问题]5.1如果两家是同时决策,有纳什均衡吗?答:有,是(后面,前面)5.2如果双方采用规避风险的策略,均衡的结果是什么?答:毋需规避风险.5.3如果电视台1先选择,结果有什么?若电视台2先选择呢?答:如第1题,按反向归纳法解.若1先选择,结果为(23,20);若2先选择,结果为(23,20).5.4如果两家谈判合作,电视台1许诺将好节目放在前面,这许诺可信吗?结果可能是什么?答:不可信.因为该博弈只有一个纳什均衡,在该均衡中1选择将好节目放后面.6两个厂商(A与B)考虑健康雪茄的竞争品牌.厂商报酬如表所示:B生产不生产A生产3,35,4102
第十一讲广延性博弈……不生产4,52,26.1这个策略有纳什均衡吗?答:有,分别为(生产,不生产)和(不生产,生产).6.2这个对策对于厂商A或者厂商B有先动优势吗?答:有.若A先选择,它将选择“生产”,B随之必选择“不生产”;这样结果为(5,4).同理,若B先选择,将有结果(4,5).因此,两家厂商做先行动者比后行动者收益均大1,即,两家厂商皆存在先动优势.6.3厂商B发现厂商A欺骗,能把它赶出市场吗?答:“欺骗”的定义这里没有给出.不过没有关系,B没有任何可行的策略能使A利润小于零.所以B无法把A赶出市场.7WET公司垄断了震动充水床垫的生产.这种床垫的生产是相对缺乏弹性的——当价格为每床1000美元时,销售25000床;当价格为每床600美元,销售30000床.生产充水床垫的唯一成本是最初的建厂成本.WET公司已经投资建设生产能力达到25000床的工厂,滞留成本与定价决策无关.注:“滞留成本”为sunkcost的另译,这里指25,000床的生产能力所用投资.7.1假设进入这个行业能够保证得到一半市场.但是要投资10,000,000美元建厂,构造WET策略(p=1,000或p=600)反对进入策略(进入或不进入)的报酬矩阵.这个对策有纳什均衡吗?答:报酬矩阵如下,支付的单位为million.潜在进入者进入不进入WET$1,00012.5,2.525,0此时市场为25,000床,价格为1000美元.$6009,-115,0此时市场为30,000床,价格为600美元.有纳什均衡($1000,进入).7.2假设WET公司投资5,000,000美元将现有工厂的生产能力扩大到生产40,000床充水床垫.阻止竞争对手的进入是有利可图的策略吗?答:此时报酬矩阵如下:潜在进入者进入不进入WET$1,0007.5,2.520,0$6004,-113,0显然,生产能力的扩充不能阻止对手反而降低自身均衡利润水平,只要进入行业能保证得到一半的市场,市场进入对潜在进入者就是有动力的.8解下列广延型博弈:103
第十一讲广延性博弈……解:该博弈有唯一子博弈纳什均衡((L,L′),L′′).9讨论本讲中的“蜈蚣博弈”(见图11.3),若三方都采取“向前看”的态度,有没有“妥协”并使三方都获利的可能?这对讨论中国的“债转股”问题有什么启发?答:“债转股”是指国家在1999年将国有企业的部分债务转为股份性质,并设立四家国有资产管理公司进行管理.这部分债务总额高达2万亿人民币,但偿付率很低,即真实价值很低.更进一步的了解就很少了.不过可以提一下的是,中心的讨论稿只有林毅夫2000年有篇文章以此为主题,国企的问题根源仍在政策性负担上.10考虑下列广延型博弈:10.1写出该博弈的策略型博弈形式.解:策略型博弈形式为:2(L′,L′)()L′,R′(R′,L′)(R′,R′)1L3,13,11,21,2R2,10,02,10,010.2该策略型博弈中有纳什均衡吗?答:有,它们是(L,(R′,R′)),(R,(R′,L′)).104
第十二讲子博弈与……第十二讲子博弈与完美性1在Bertrand价格博弈中,假定有n个生产企业,需求函数为p(Q)=a−Q,其中p是市场价格,Q是n个生产企业的总供给量.假定博弈重复无穷多次,每次的价格都立即被观测到,企业使用“触发策略”(一旦某个企业[未]选择垄断价格,则执行“冷酷策略”).求使垄断价格可以作为完美均衡结果出现的最低贴现因子σ?解释σ与n的关系.解:设任一生产企业的边际成本恒为c,a>c>0.由需求函数知边际收益ma+cma−cp=Q=MR=a−2Q,令MR=MC,得垄断价格2,垄断产出2,垄()2()2a−cma−cπ=i断总利润4,企业i在一个时期可获得利润4n,i=1,2,...,n.考虑时期t企业i的选择.给定其它企业按照垄断条件生产,若企业仍遵守垄断定价,那么它从t期到无穷的的利()2a−cπ()m=i()润的现值4n1−σ,m代表垄断定价.mn−1()Q=a−c−i,t给定其它企业按照垄断条件生产,即2n;若企业i选择背离垄断价格,追求利润最大化的问题是(m)maxQa−Q−Q−cQitii,t−i,t,Qi()2()2n+1n+1a−cQ=()a−cπ=i,ti,t2由一阶条件得到4n,此时,16n.又因为在t期,企π()b=π业i不遵守垄断定价规则,从t+1期开始,它的利润都是零.因此,ii,t,b代表背叛垄断定价.2⎛2⎞σ=⎜1−⎟令πi()m=πi(b),得⎝n+1⎠时,因此使企业i将保持垄断定价,又所有企业相同,由此垄断价格可以作为完美均衡结果出现的最低贴现因子为2⎛2⎞σmin=⎜1−⎟⎝n+1⎠.105
第十二讲子博弈与……dσ4min()=n−1≥0()3又dnn+1,且当n≥2时,不等式严格成立,因此σmin随n的增加而增加.即,当n越大,不遵守垄断规则,图一时好处,不顾未来收益的吸引力就越大,因此,只有更高的折现率,提高未来收益在利润中的权重,才能保持厂商遵守垄断规则.2下表给出了一个俩人的同时博弈,若这个同时博弈进行两次,第二次博弈是在知道第一次博弈的前提下进行的,并且不存在贴现因子.收益(4,4)能够在纯策略的子博弈完备的纳什均衡中作为第一次博弈的结果吗?如果它能够,给出策略组合;如果不能,请说明为什么不能.2LCRT3,10,05,01M2,11,23,1B1,20,14,4[我将“不存在贴现因子”理解为“贴现因子为1”]解:若该博弈为一次博弈,有两个纯策略纳什均衡(T,L),(M,C),和一个混合策略纳什均衡()()0.5,0.5,0,()0.5,0.5,0.三个均衡分别对应结果(3,1),(1,2)和(1.5,1.5).之所以(4,4)能在纯策略的子博弈完美纳什均衡中作为第一次博弈的结果,是其中一方都可以威胁对方,如果对方不在第一次博弈时选择(4,4)所对应的行动,第二次博弈时将采取最小化对方最大化收益的行动,如果对方在第一次选择了(4,4)所对应的行动,第二次博弈时将采取最大化对方最大化收益的行动.并且给定对方的行动,威胁者无动力改变自己的策略.游戏者2最小化对方最大化收益的行动是C.那么,参与者2试图引导结果(4,4)的策略为:第一次选择R.如果第一次1没有选择R,那么第二次选择C;如果第一次2选择R,1将选择L.用反向归纳法.第二次博弈必然是纳什均衡,(T,L)或(M,C).考虑第一次博弈,给定2选择R,1如果选择T,那么两时期的收益现值为6,如果选择B,该现值为7.因此,1在第一次博弈中会选择B.综上,给定2的策略,1的可能策略之一是,第一次选择B,第二次选择T.106
第十二讲子博弈与……然后考虑给定1的这个策略,2是否有动力偏移自己的策略.第二期的选择必然是纳什均衡,无动力偏移.而在第一次博弈中,给定1选择B,2必然选择R.因此2没有动力偏移自己的策略.因此(4,4)能够作为第一次博弈的结果.其均衡策略组合为参与者1:第一次选择B,第二次选择T.参与者2:第一次选择R.如果第一次1没有选择R,那么第二次选择C;如果第一次2选择R,1将选择L.注:事实上,只要1的策略满足“第一次选择B,然后如果2第一次选择R,第二次就选择M”就可以了.进一步地,1非均衡路径上的行动不影响结果.因为,第二次选择的行动必然是一次博弈中的纳什均衡;同时,1无法也没有必要威胁2第一次要选择R(无法:我们的均衡路径上,给定第一次博弈结果,2的均衡收益已经最小化;没有必要:R是2在第一次博弈中,给定1选择B的占优行动).3什么是重复博弈中的策略?什么是一个重复博弈中的子博弈?什么是一个子博弈完美纳什均衡?答:重复博弈中的一个策略规定了第一次博弈的选择的策略,规定了在除第一次博弈外的任何一次博弈中,对应该次博弈前任一策略组合序列,所要选择的策略.[或:记重复博弈为Γ()n,它的任一次博弈记为ΓN[I,S,{u(⋅)}],I为参与者的集合,S和u()⋅分别标志所有参与者的策略集的幂集和该参与者在给定策略组合时的收益.t−1nHt=∏SH=UHtS记i=1,为在t时期的博弈“历史”,又记t=1.若i为参与者i在一次博弈中的策略集,那么映射HaSi为行动者i在重复博弈Γ(n)中的策略.博弈为无限次重复时,定义方式类似.]重复博弈的子博弈,是某次博弈的一个策略组合以及该次博弈后的所有博弈.重复博弈的子博弈完美纳什均衡,是对该重复博弈的任何子博弈来说都是纳什均衡的策略组合.4在一个由n个企业组成的古诺寡头经济中,市场需求的反函数为p(Q)=a−Q,这里Q=∑qii.考虑以此为基础的一个无穷期重复博弈.为了在一个子博弈完美纳什均衡中运用“触发策略”(一旦某企业违背了产量卡特尔定下的额度,则全体企业都会执行107
第十二讲子博弈与……冷酷战略,实行古诺模式中的个别企业最优产量),贴现因子最低应为多少?当n变化时,δ的最低值要求会有什么变化?解:该题与第一题相同.5考虑下列三阶段的谈判博弈(分1美元)(1)在第一阶段,游戏者1拿走1美元中s1部分,留给游戏者2的是1−s1;2或者接受1−s1(博弈结束),或拒绝1−s1.(2)第二阶段,2提出,1得s2,2得1−s2.1或接受s2(博弈结束),或拒绝.(3)在第三阶段开始,1获s,2获1−s.0δ(1−s),所以这里把它略去了.109
第十三讲委托–代理……第十三讲委托–代理理论初步21一家厂商的短期收益由R=10e−ex给出,其中e为一个典型工人(所有工人都假设为完全一样的)努力水平.根据下列每种工资安排,确定努力水平和利润水平(收入减去支付的工资).解释为什么这些不同的委托代理关系产生不同的结果.1.1对于e≥1,w=2;否则w=0.解:该工资安排将使工人努力水平确定在e=1上,此时,利润为π=R−w=8−x.1.2w=R2.d⎛R(e)⎞4⎜−e⎟=0e=解:此时工人愿投入的最佳努力水平由de⎝2⎠决定,即x.此时,利12润为x.1.3w=R−12.5.d9[]()R()e−12.5−e=0e=解:此时工人愿投入的最佳努力水平由de决定,即2x.此时利润为12.5.这些关系不同在于(1)典型工人努力的边际激励,和(2)典型工人可接受的最低收入水平.这两者使它们产生不同的结果:不同(1)使厂商与工人的剩余之和不同,不同(2)使剩余在两者间分配结果不同.2假定有几位企业家,每位企业家都有一个投资项目,每个项目的回报,R,是服从于[]a,b上的均匀分布的,这里a=100,b=150.每个项目的成本为100,而所有的企业家都没有自有资金.若银行向企业家贷款,银行是委托人,企业家则成了代理人.银行为了观察与监督企业家对资金的使用情况,则要在每一项目上花费5(观察的成本)2.1项目的期望毛回报E()R是多少?a+bE()R==125解:由于R属于[]a,b上的均匀分布,所以2.2.2如果银行需要25%的利率去吸引存款,上述项目能从银行贷到资金吗?解:除去利息因素,该项目对每一个企业家的期望利润为25.而银行贷款100给一个项目,其成本是30,包括支付存款利息25,和对该项目的考察成本5.即使企业将所有的利润给银行,对每一个项目,银行都仍有5的损失.因此上述项目是无法向银行110
第十三讲委托–代理……贷到款的.2.3如果银行以10%的利率去吸引存款,又要监管所有项目,则银行从项目的回报R中,要分多少的百分比才能使银行收支相比.解:银行现在给每个项目贷款的成本为15.又除去利息支付,项目的期望回报为125.那么银行需要分92%(115/125)才能收支相抵.2.4(3)问中的分享合约在有监督成本的条件下能产生纳什均衡吗?为什么?解:这里监督成本固定且意味着由此不存在信息不对称情况(正如题目所言,)会产生纳什均衡,对预期纯利润的任何一种分配方式都是纳什均衡.3考虑一个道德风险模型.在这里,所有者是风险中立的,而代理人的偏好是被定义于其收入w的均值与方差以及付出的努力e上,代理人的效用为E()u=E()w−φVar(w)−g(e)这里,g()e代表代理人的努力成本,且g′(0)=0;g′(e),g′′(e)(),g′′′e>0,且limg′()e=∞e→∞.e的可能值为e∈R+.利润π是取决于e的,并且π服从整正态分布,2其均值为e,方差为σ.3.1考虑线性契约w()π=α+βπ,证明:当w(π),e与σ2给定时,代理人的期望效用22()为α+βe−φβσ−ge.证明:E()w=E(α+βπ)=α+βE(π)=α+βe,()()2()22Varw=Varα+βπ=βVarπ=βσ.代入代理人的效用函数,得到代理人22()的效用为α+βe−φβσ−ge.3.2推导:当e可观察时的最优契约.解:e可观察时,委托人可以直接规定利润最大化努力水平,并在达到最优努力水平时给与代理人其保留效用水平的工资.利润最大化努力水平由maxE()()π−Ew+E(u)e决定,其一阶条件为g′()e=1.g′()()e,g′′e>0*g′e*=.由于当e>0时,.所以存在唯一的一个努力水平e,使得()1**记代理人的保留效用水平为r,且如果r≤e,那么,最佳契约就可以为,如果e≥e,*w=r,否则w=0;如果r>e.那么最佳契约为,w≡0.3.3当e是不可观察时,请导出最优线性契约.解:这里先假设r=0.111
第十三讲委托–代理……给定w的决定,那么代理人的最大化问题是:(22())maxα+βe−φβσ−gee从一阶条件得到g′()e=β明显β>0,同3.2,给定任何一个β,都存在一个唯一的努力值满足该条件,记该1e′()β=>0函数关系为e()β,当β>0时,有e(β)>0,g′′()e,g′′′()ee′′()β=−<03[]g′′()e.当β=0时,有e(0)=0.给定代理人的努力水平e()β,委托人的最大化目标为:maxE()(e()β−Ew)α,βs.t.E(u)≥0()()()[()]()(22())构造拉格朗日函数L=Eeβ−Ew−λ−Eu+0=eβ−φβσ−geβ.它最大化的一阶条件为1−g′()e()β1−ββ=e′()β=e′()β222φσ2φσ,λ=1e′(β)β=2**有e′()β+2φσ,由它确定值β=β.将它带入个人理性约束,得到α=α**=g(e()β**)()+φβ**2σ2−β**e(β**)****因此,最优线性约束为w=α+βπ.**注:β是唯一的.理由如下:补充定义g′′(0)=g′′(0+)≥0,为了方便起见,先假1e′()0=>0设它严格大于零.此时g′′()0.e′()βf()β=β−()2记e′β+2φσ,f(β)在[0,1]上连续.有f(0)<0;当β≥1时,e′()β<1()2e′β+2φσ,所以f()β>0.112
第十三讲委托–代理……222φσe′′(β)2φσg′′′/g′′f′()β=1−=1+>022又当β∈()0,1时,[]e′()β+2φσ()1+2g′′φσ.所以在(0,1)**上存在唯一的β使得f()β=0.如果g′′()0=0,那么有e()0=∞,f(β)在β→0时,仍然有f(β)<0;其他结论完全相同.E={e,e,e}4考虑下列“道德风险”模型:代理人的行为有三种可能,123;而理论π的结果只有两种πL=0与πH=10.高水平的πH是取决于努力水平e的,具体的条件概率为f()πH|e1=2/3,f(πH|e2)=1/2,f(πH|e3)=1/3;代理人的努力成本函数为g()e1=5/3,g()e2=8/5,g(e3)=4/3.代理人的效用函数为v()w=w,并且代理人的保留效用为u=0.求解:4.1当e是可观察时,什么是最优契约?解:事实上代理人的效用函数为,u(e)=v(w(e))−g(e),根据个人理性约束,委托2()w=ge.因此对应e的期望利润为人将始终保持代理人的剩余为零.也就是说,1()(2)356114π=fπ|eπ−ge=π=π=1H1H12e39,同理对应e2有25,对应3有9.显π>π>π然123.委托人需要代理人选择e1.所以,可行契约为,w=25/9,当e=e;w=0,当为其他情况.1g(e)要等于多少才能使e4.2证明:若e不可观察,则e2是不会被代理人付诸实施的.22被代理人付诸实施?解:e不可观察,意味着只能根据利润水平确定工资水平.记⎧wH,π=10w=⎨w,π=0⎩L那么代理者的效用水平为113
第十三讲委托–代理……⎧20.510.55w+w−,e=e⎪HL1333⎪()⎪10.510.58ue=⎨wH+wL−,e=e2⎪225⎪10.520.54w+w−,e=e⎪HL3⎩3330.50.52w≥w+u(e)≥u(e),即LH5所以选择e=e2,需要满足21,以及满足0.50.58w≤w−u()()e≥ueLH23,即5.显然两式是矛盾的.所以e2不可能实施.()0.50.50.50.5ge=gw≤w−6g+10w≥w+6g−8令2,则以上条件为HL,HL.所以,3g≤当2时,e2可能实施.g()e=8,且f()π|e=x∈(0,1),如果e是可观察的,什么是x→1时的4.3假定1H1最优契约?解:当x→1时,若引导代理人选择e1,那么委托人期望利润趋近并严格小于2.与4.1中的结果比较,这时,引导代理人选择e2可以获得最大期望利润.可行契约为,w=64/25,当e=e2;w=0,当为其他情况.5考虑下列基本的代理人模型(2)y=kα+ε,ε服从N0,σ这里,y为代理人对委托人的贡献,α是代理人的努力程度,k>0为阐述(k可代表委托人为代理人所创造的工作环境与技术装备,k越高,则给定α会产生更大的贡献.又假定,委托人与代理人都是风险中立的.代理人的努力成本函数为C()α.求解:5.1假定委托人与代理人之间签订一个线性合约w=s+by.代理人会采取什么行动?代理人的行动α会如何随b发生变化?代理人的行动会如何随k而发生变动?114
第十三讲委托–代理……解:代理人的期望剩余为s+bEy−C(α)=s+bkα−C(α)最大化问题是maxs+bkα−C()αα满足于s+bkα−C()α≥0不考虑约束,从无条件最大化的一阶条件得到C′(α)=bk.*s+bkα*−Cα*≥,代理人会将工作努力保持在记满足该条件的α=α,如果()0边际成本等于bk的水平上.由于(一般情况下)C′′(α)>0,因此,随着b、k的增加,α也会增加.*(*)若s+bkα−Cα≥0不满足,代理人将选择α=0,且b、k的变化均不影响努力水平.5.2现在假定代理人的效用函数形式为()−rxux=−e()12Cα=α又假定代理人努力成本为2.*证明:最优线性契约中的激励系数b必满足2*kb=*2k+rσ22⎧rbσ⎫Eu()w=exp⎨s+bkα−⎬证明:令x=w=s+by=s+bkα+bε,有⎩2⎭.因此,给定b,s满足代理人个人理性约束,代理人的最优努力水平由22rbσ12maxs+bkα−−αb222b()22s+k−rσ确定,即α=bk,此时,代理人的效用水平为2委托人的问题是()2max1−bkb−sb,s2b()22s+k−rσ≥0满足于2115
第十三讲委托–代理……2kb=22构造拉格朗日函数,并解得k+rσ.2*kb=*22因此,最优线性契约中激励系数b满足k+rσ.6与第5题的情况类似,代理人对委托人的贡献为(2)y=a+ε,ε服从N0,σ委托人与代理人都对风险中立.只是代理人的努力成本函数为()2Ca=ma,m>0问:6.1若委托人与代理人签订了一个线性合约w=s+by.代理人会采取什么样的a?a会怎样随b而发生变动?a会如何随m而变动?(())2解:代理人的期望收益水平为Ew−Ca=s+ba−ma,因此,代理人的最大化问题为2maxs+ba−maa2满足于s+ba−ma≥0ba=不考虑约束,从无条件最大化一阶条件中得到2m.2bbs+≥0a=如果4m,代理人将选择2m,并且a随着b的增加而增加,m的减少2bs+≥0而减少.如果4m不满足,代理人将选择a=0,并且不受b、m变化的影响.()−rx6.2现在假定,代理人是风险规避的,其效用函数为ux=−e.*证明:在最优线性契约中,激励系数b必满足*1b=21+2mrσ证明:给定b、s满足个人理性约束,代理人的最大化问题为222rbσmaxs+ba−ma−a2116
第十三讲委托–代理……222bbrbσa=s+−其一阶条件为2m,此时代理人的剩余为4m2.委托人的最大化问题是2bbmax−−sb,s2m2m222brbσs+−≥0满足于4m2.1b=2构造拉格朗日函数,解得1+2mrσ.*1b=*2因此,最优线性契约中,激励系数b满足1+2mrσ.117
第十四讲信息不对称……第十四讲信息不对称、逆向选择与信号博弈1假定二手车的质量q是服从于[t,z]上的均匀分布,t>0.卖主效用函数为u1=−pn+qn,其中n∈{0,1}为购买数量,p为价格,;3u=−pn+µn2n∈{0,1}买主效用函数为2,其中为出售数量,p为价格,µ为对市场二手车质量的期望值.[原文为“在本讲给出的u1与u2形式下,(见公式(14.1)–(14.9)).”有略微形式上的改动,不影响结果.]证明:1.1当市场价格为p时,平均质量µ必然为0.5t+0.5p,p≥t.u()p≥0,得q≤p,即整个车市的质量将是在[t,p]上均匀分布.所以,证明:令1tp+质量期望值µ=Eq=22.1.2市场不会彻底萎缩.t+zµ=0证明:记2为初始市场质量期望,那么,第1期市场消费者的最高保留价格3⎡3⎤p1,1=µ0⎢t,µ0⎥为2,因此在第2期,质量分布就在⎣2⎦.考虑k+1期市场,质量分1µk1=()t+p1,k[t,p1,k]+2布为时,质量期望值则为,而买主的保留价格为33p1,k1=µk1=()t+p1,k++24333p−p=tp=()t+z1,k+11,k1,1解差分方程44,初始条件为4,解得:k⎛3⎞()pk=⎜⎟−3t+z+3t⎝4⎠.limp=3tk有k→∞.118
第十四讲信息不对称……即,若z≥3t,那么市场的均衡就是质量均匀分布在[t,3t]之间,市场的均衡价格为3t;如果z<3t,那么市场的均衡就是质量均匀分布在[t,z]上,市场均衡价格在区间⎡3()⎤z,t+z⎢⎥⎣4⎦上.综上,市场不会彻底萎缩.注:还有一种更直观的办法.即,在均衡中,当依据质量的分布[t,p],得到期望质量3()t+p既而得到买家保留价格4,而这个值恰好等于质量分布上限.即有3p=()t+p4e解得结果p=3t.而,z<3t时的结果可以直观得得到,区间的上下限分别是均衡时买家和卖家的保留价格.1.3与信息完全相对照,关于q的信息不对称使交易缩小了多少?使买卖双方的利益损失了多少?z⎛3⎞122∫⎜q−q⎟dq=()z−t解:在信息完全条件下,买家与卖家的剩余之和为t⎝2⎠4.当z≥3t时,交易缩小量为L=z−3t.3t()2∫3t−qdq=2t此时卖家的剩余为t,买家剩余为零.1(22)z−9t所以买卖双方的剩余之和减少了4.当z<3t时,交易无缩小.z12∫()z−qdq=()z−t但此时卖家剩余大于或等于t2.2假定二手车市场上的质量仍服从[0,2]上的均匀分布,但卖主与买主一样不知道产品质量.其他情况与本讲第一节完全一样[效用函数与第1题相同].证明:在以上条件下,市场均衡时会有p>0,q>0.并且不存在逆向选择.119
第十四讲信息不对称……证明:由于双方均不知车的质量,所以对双方而言车的质量等于其期望值1.代q=1入卖家效用函数,令u1=−np+nq=0,得到保留价格p=1,同理,代µ=1入买家效用函数,并令u2=0,得到保留价格1.5.因此,所有交易均会成交,成交量q>0,成交价格p∈[1,1.5],也有p>0.不存在逆向选择.3在本讲第二节所描述的Salop-Stiglitz一时期的质量模型中,如果ap0时,L+de−ee时,120
第十四讲信息不对称……**H+de−ke0,v′′<0.在未发生事故时,其财产为Ig=1−p,发生后其财产Ib=I−L−p+s.所以,他的期望效用E()(u=1−θ)v(I)+θv(I)gb未发生事故,保险公司的利润为p,发生时为p−s.所以它的期望利润E()π=p−θs6.2如果保险公司要选择s与p,来确保max(p−sθ)s,p应该满足投保人什么样的“约束”?解:应该使投保人的效用不低于投保前的效用.即,E(u)≥θv(I)(+1−θ)(vI−L).6.3解出(2)列出的数学规划,证明最优赔偿金s应满足s=L.解:构造拉格朗日函数Λ=p−sθ−λ[]()1−θ(v(I)−v(I−p))+θ(v(I−L)−v(I−L−p+s))一阶条件为:∂Λ=1−λ()1−θv′()(I−p−λθv′I−p+s−L)=0∂p∂Λ=−θ+λθv′()I−p+s−L=0∂p由第二个条件得到1=λv′()I−p+s−L122
第十四讲信息不对称……代入第一个条件,得到1=λv′()I−p综上,v′()I−p+s−L=v′(I−p).又v′′<0,说明v′单调,所以,I−p+s−L=1−p,即s=L.7福格小姐计划花10,000美元旅行.她的效用形式为u(Y)=lnY.她在旅行中丢失1,000美元的可能性为25%.福格小姐相当愿意去为了丢失这笔钱的可能性去买保险.假如买了这种保险的人在管理现金方面都趋向于变得更粗心,那么他们丢失1,000美元的概率就会上升到30%.在这种情况下,实际的公平保险率是多少?福格小姐现在还会买保险吗?解:实际的公平保险率为30%.按照30%的公平保险率购买全额保险,福格小姐的期望效用为Eu(Y)=ln9700≈9.180;而不参加保险,福格小姐的期望效用Eu()Y=0.25ln9000+0.75ln10000≈9.184.比较两种情况,福格小姐现在不会买保险.8我们在本讲第四节研究了分担的健康保险政策,并且表明风险厌恶者会愿意购买全额保险.然而,假定买了费用分担保险的人会更好地照顾他们自己的健康,这样,他们在生病时所遭受的损失就由10,000美元下降到7,000美元.现在,费用分担保险的公平价格实际上是多少?与全额保险相比,一些人会偏爱费用分担保险,这是可能的吗?什么会决定个人是否会有这样的偏好?(对于本题,只用图形来说明就可以了.)解:第四节有模型,但是没有具体的数值.可以预见的是,实际自负损失降低了3,000美元.而偏爱费用分担也是可能的;在生病概率θ不变的情况下,存在一种费用分担和价格的组合()D,p,使得在生病情况下,收入水平与参加全额保险而生病时相同.也就是说,使得−7000p−D=−10,000θ,而在未生病时有−7000p>−10,000θ.也就是说,存在费用分担和价格的组合,使得选择集包括全额保险的选择.而生病与未生病1−θ1−p的相对价格的变化:从θ到p,这意味着对一定形式的偏好,将会选择费用分担计划.9蓝眼睛的人会比棕眼睛的人更容易丢失他们的贵重手表.具体地说,蓝眼睛的人一年之内就会丢失他们100美元的概率为80%,而棕眼睛同样的概率却只有20%.蓝眼睛的人和棕眼睛的人在人口中有同样的代表性.9.1如果保险公司假定蓝眼睛的棕眼睛的人具有同样的可能去买手表丢失保险,实际上公平的保险费率会是多少?答:实际上会是50%.9.2如果蓝眼睛与棕眼睛的人有对数效用–财富函数,并且每个人当前的财富都是10,000美元,那么,这些人会不会以(1)的保险费率购买手表保险?123
第十四讲信息不对称……答:对蓝眼睛的人,不买保险的期望效用为0.8ln9900+0.2ln10000≈9.20230,对棕眼睛为0.2ln9900+0.8ln10000≈9.20833;所有的人买了保险效用水平为ln9950≈9.2053.因此,蓝眼睛会买,而棕眼睛不会买.9.3给定(2)的结果能否正确计算保险费率,它应该等于什么,每一类型的人的效用会怎样.答:不能.此时保险费率应当按照蓝眼睛的禀性来确定.若按公平保险率计算,保险率为80%,此时蓝眼睛的效用约为9.20231.而棕眼睛的效用不变.9.4假定保险公司对蓝眼睛的人和棕眼睛的人要收不同的保险费率.这些人的最大化效用与(2)和(3)中所计算的效用相比会怎样?解:两种不同的保险费率为,蓝眼睛80%,棕眼睛20%.蓝眼睛的效用增加了0.00001,棕眼睛的效用约为9.20834,也相较前增加了0.00001.10假定有两类工人:高能力的工人与低能力的工人.工人的工资由他的能力决定——高能力的赚50,000元,低能力的赚30,000元.厂商不能测度工人的能力,但是它却可以了解到工人是否有高中文凭.工人的效用由他们在工资上与为获得文凭所支付的费用上的差异所决定.10.1如果高能力工人与低能力工人在获取高中文凭中的花费是一样的,那么,在这种情况下,是否可以存在一种高能力工人拿高工资、低能力工人拿低工资的分离的均衡?答:不可能.如果存在这样的均衡,显然只有某一类工人去获取高中文凭,否则必然是混同均衡.给定厂商的规定,有文凭的工资50000元,其它为30000元.那么高能力的获取高中文凭,这说明高工资减去教育成本,所得大于低工资不教育.但对低能力的也是这样,对他们而言,50000的工资减去教育成本,所得必然也大于低工资不教育.因此,低能力也会去获得文凭.而给定没文凭30000元,有文凭50000元,那么显然所有人都不会要文凭.所以,不存在这样的分离均衡.10.2高能力的工人为了获得高中文凭所愿意支付的费用数量是多少?如果有一种文凭可以让雇主去识别高能力工人的话,为什么对于低能力工人来说,这种文凭一定要其花费更多?答:最多支付20000元(给定混同均衡收益为30000元).仍然考虑厂商的规定,有文凭的工资50000元,其它为30000元.对高能力工人来说,必然有50000元减去教育成本大于30000元,而对低能力工人来说,50000元减去教育成本小于30000元;这就意味着高能力的教育成本要低于低能力的教育成本.124
第十五讲工资、寻找工作……第十五讲工资、寻找工作与劳动市场中的匹配1偏远小镇上,独一公司是唯一的雇主.该公司对劳动力的需求为w=12−2L,其中w是工资率.劳动供应函数为w=2L.1.1独一公司作为垄断买方,它的边际劳动成本是多少?()2解:给定劳动供应函数,公司的劳动总成本为C=wLL=2L,边际劳动成本为MC=4L.1.2独一公司将雇佣多少工人?工资率是多少?解:令12−2L=4L,得到工人雇佣量L=2,工资为w=2L=4.1.3如果当地的最低工资率是7元,独一公司将雇佣多少工人.⎧7,0≤L≤3.5w=⎨2L,L≥3.5解:最低工资率为7元意味着劳动供给曲线为⎩,由此可得到边际⎧7,0≤L≤3.5MC=⎨4L,L>3.5劳动成本⎩.令12−2L=MC,解得L=2.5.因此,独一公司将雇佣2.5个工人(考虑工时,所以有半个劳动力的说法).1.4假设劳动市场不是买方垄断而是完全竞争的,(2)、(3)两问题的答案又是什么?解:令12−2L=2L,得到L=3;工资率为w=2L=8.最低工资率定为7元后,又令需求等于供给,得到L=2.5.2一个人由每天的收入Y得到的效用为()2uY=100Y−0.5Y收入的唯一来源是劳动所得.因此,Y=wL,这里w是每小时的工资,L是每天工作的小时数.这个人知道有一个职位,一天固定工作8小时,每小时工资5美元;对于另一个职位,每天工作时间是随机的,平均值为8小时,标准差为6小时,必须提供多高的工资才能使这个人接受这项更“冒险”的工作.解:考虑第一个职位,日工资Y=40美元,效用水平u(40)=3200.考虑第二个,设工资为w,那么日工资Y=wL,效用水平()222uwL=100wL−0.5wL.其期望值Eu(wL)=800w−50w.125
第十五讲工资、寻找工作……令Eu()wL=u(40),解得w=8.即必须提供8美元每小时的工资才能让他接受这项工作.3一个有两个成年人的家庭试图将如下形式的效用函数最大化u()C,H,H12这里C是家庭消费,H1与H2是每个家庭成员享受的闲暇时间.选择的约束条件为C=w()24−H+w(24−H)+N1122这里w1与w2是每一家庭成员的工资,而N是非劳动所得.∂H2∂w3.1这里不作数学推导,只运用替代与收入效应的概念讨论交叉替代效应1可能的符号.′解:假定w1上升到w1,为了讨论替代效应,将预算约束转化为C=w′()24−H+w(24−H)+N−g,1122g=()w′−w()24−H.其中111w′1w因为H1与H2的相对价格上升到2,所以可以预见H1减少,H2增加.C=w(24−H)+w(24−H)+Ng后.如果在给讨论收入效应,预算约束加上1122∂H2定()C,H1,H2处,H2的收入弹性为负,那么无法确定∂w1的符号;如果为正,那∂H2∂w么1为正.3.2假定有一个家庭成员(比如,个人1)可以在家里劳动,从而可按如下函数将闲暇时间转换为消费C=f(H),f′>0,f′′<011这一额外选择方式会如何影响工作在家庭成员之间的最优分配?解:如果1选择在家里劳动,那么家庭的约束变为:C=w()24−H+N22效用函数变为u(C+C,H,H)112126
第十五讲工资、寻找工作……家庭将比较成员1在家里劳动的最大效用值与在外劳动的最大效用值.由此来决定工作方式.如果1可以选择在家里劳动一段时间,又在外劳动一段时间(更实际的情况),那么f′()H≥w的时间内选择在家劳动,然后剩下的时间出去工可以预见的是,1将在11作.因为这样1和2的休息量可以仍保持在原有水平,而消费额C+C1+N却大于不在家劳动的最优消费额.4卡尔在一个孤岛上拥有一个大服装厂,对大多数岛上居民来说,卡尔的工厂是唯一的就业途径,因此卡尔的行为如同买方独家垄断着.制衣工人的供给为L=80w,L为劳动数量,w是每小时的工资率假定卡尔的劳动需求(边际收益)曲线方程为L=400−40MRPL4.1为使利润最大化,卡尔会雇用多少工人,付多少工资?LMC=解:从供给曲线得到劳动边际成本为40,令MRPL=MC,得到L=200.即卡尔会雇用200名工人,工资率为2.5.4.2假如政府实行最低工资制.当最低工资定在每小时4美元时,卡尔会雇多少工人,又有多少人会失业?⎧4,L≤320⎪MC=⎨L⎪,L>320解:这时劳动边际成本为⎩40,令MC=MRPL,解得L=240.如800L=果没有最低工资制,在完全竞争市场,就业水平为3.因此失业率为()800/3−240=10%800/3.4.3图示你的结果.127
第十五讲工资、寻找工作……240266黑色粗线为需求曲线,暗红色为MC;供给曲线为黑细线.4.4在买方独家垄断的情况下,实行最低工资制与在完全竞争的情况下实行最低工资制,,结果有什么不同?答:在该题目中,没有不同.5假定一个人知道某一种彩色电视机的价格服从在300美元与400美元之间的均匀分布.此人打算通过电话来获得价格的多少?5.1如果此人打了n次电话询问价格的话,请计算出所要支付的预期最小价格.100300+答:n+1,n>1.打的每一个电话得到的结果同样服从300到400美元的均100300+匀分布,所以可以知道其中最低价格的期望值为n+1.5.2请表示所要支付的预期价格以一种递减的比率随n下降.100100300+f()x=300+答:n+1是x+1上的一系列点,因为f′<0,f′′>0,所以所要支付的价格以递减的比率随n下降.5.3假定根据时间与努力,打一次电话要花2美元.为了通过搜索得到最大化,这个人应该打多少次电话?100−300−−2k答:设这个人应该打k次电话.其总收益为k+1,最大化条件为k=9.即,这个人应该打9次电话.6设某就业市场工资率是均匀分布在1000元与2000元之间的.你目前的工资是1500元.若你要找新工作,每一次面试会使你花费50元.你认为在就业市场上再照一次新工作合算吗?为什么?128
第十五讲工资、寻找工作……1000−+2000−50i解:解题逻辑同上题.设面试次数为i,那么预期收益水平为i+1,最大化条件为i=25,因为i=4时,收益水平为1600元,i=5时约为1573元.所以找工作经过4次面试后,预期收益最高为1600元,大于现有工资,再找一次工作合算.7在萨莫斯1988年的论文中,他指出,“在一种效率工资的环境里,那些不得不对工人支付工资升水的企业只遭受二阶损失.几乎在所有的看似合理的谈判框架里,这都回使工人容易从企业那里获得让步.”这个题目是让你去研究萨莫斯的上述论断.考虑一个企业,其利润由下式决定:()αeLπ=−wLα,0<α<1工会有一个目标函数u=()w−xL[按郭宏波的改正,似更合理.此处原为u=w−x]这里,x是工人们的外在工作机会.假定企业与工会之间就工资进行谈判,在w给定时由企业选择L(就业量).7.1假定e≡1,从而不存在效率工资的考虑.7.1.1当w给定时,企业会选择多大的L?什么是相应的利润水平.∂πα−11=L−w=0∂LL=wα−1,相应解:给定w,令,得到利润最大化的L水平为α⎛1⎞−−1w1−α⎜⎟利润水平为⎝α⎠.γ1−γ7.1.2假定企业与工会共同选择w去使uπ最大化,这里,0<γ<α,γ表示工会的谈判力量.他们会选择多高的w?1u=()w−xwα−1解:接上题,利润最大化时,工会效用因此最大化问题为γ⎡1−γα()1−γ⎤⎡γ−1−α⎤⎛1−α⎞−1−αmax⎢()w−xw⎥⎢⎜⎟w⎥w⎢⎝α⎠⎥⎣⎦⎣⎦对目标函数取对数,并从一阶条件得到⎛γ⎞w=x⎜1−γ+⎟⎝α⎠.129
第十五讲工资、寻找工作……∂lnw7.1.3当γ=0时,∂γ是多少?其经济含义是什么?⎛γ⎞∂lnw=1−1lnw=lnx+ln⎜1−γ+⎟解:对上题结论取对数,得⎝α⎠,因此,∂γγ=0α.其经济含义是,赋予工会谈判力量后,工资提高的边际百分比率大于零,而且工人的边际生产率越大,这个百分比率约小.β⎡w−x⎤e=⎢⎥7.2假定⎣x⎦,这里0<β<1.7.2.1当w给定时,企业会选择多大的L?相应的利润水平是多少?解:企业现在的最大化问题为1ααmaxeL−wLLα从一阶条件可以得到1α−L=w1−αe1−α相应利润水平为α⎛1⎞⎛e⎞1−απ=⎜−1⎟⎜⎟⎝α⎠⎝w⎠γ1−γ7.2.2假定企业与工会共同选择w去使uπ最大化,这里,0<γ<α,γ表示工会的谈判力量.他们会选择多高的w?α1−u=()w−xe1−αw1−α解:接上题,工会此时效用水平为最大化问题为1−γγ⎡α⎤α1⎡−⎤⎛1⎞⎛e⎞1−αmax()w−xe1−αw1−α⎥⎢⎜−1⎟⎜⎟⎥⎢w⎣⎦⎢⎝α⎠⎝w⎠⎥⎣⎦对目标函数取对数,并从一阶条件得到αγ−γ−αw=xαβ−α∂lnw7.2.3当γ=0时,什么是∂γ的值?效率工资提高了这个弹性值了么?是否如萨莫斯所隐喻的那样,由于效率工资的存在,工会关于工资的谈判对于工资决定产生了数学上的不同效果?130
第十五讲工资、寻找工作……∂lnw1=−1解:∂γγ=0α,效率工资对该值无影响.这说明,效率工资的存在,对于工资决定未产生不同效果.8假定存在着大量企业(共有N家),每家的利润由π=f()eL−wLf′>f′′决定,其中0,<0,L是企业雇用的工人数量,w为工资,e为工人的努力.努力由⎧w⎫e=min⎨*,1⎬⎩w⎭*给出,这里w为公平工资(即,如果企业所付的工资低于公平工资,则工人的努力付*出就按工资低于w的比例下降).假定存在L的职工,他们愿意为任何大于零的工资而工作.8.1如果企业可以以任何工资率雇用工人,什么样的工资值会使企业获得最高利润?若w的解是区间,假定企业会付该区间中的最高工资.**解:企业可能给的最高工资为w;因为在w>w时,工人不会更加努力的工作使产出增加.企业利润为:⎧⎛wL⎞*⎪f⎜*⎟−wL,wf′′因为0,<0,所以:()*1)如果f′0≤w,L=0;131
第十五讲工资、寻找工作……()*~*2)如果f′0>w,则存在一个L>0,使得f′=w.~**~当L≤LN时,w=w可行.因此,w=w.[企业雇佣量L=L]~*当L>LN时,L=LN,同时企业工资仍然保持在w=w.**8.2假定公平工资w由w=w+a−bu决定,其中b>0,u为失业率,w为该经济中的平均工资.8.2.1如果企业可以自由选择工资w(当w与u给定时),有代表性的企业会如何决定w?*解:根据上问的结论.在任何条件下,w=w.8.2.2在什么条件下,劳动市场会包含一个正值的失业率u,并且该均衡不会对企业选择w造成制约?~~解:静态条件当L>LN时,不存在一个为正值的失业率.当L≤LN时,存在一个为非负的失业率,但是该均衡会对企业选择w造成制约,除非在u=ab得到*w=w的条件下,这时失业率为正.**事实上,这是一个动态调整过程.若初始条件下w≠w,经济将自动调整到w=w.***不妨假设w>w.企业先将w视为给定,并以此做出w=w的决策;这样平均工*~资率w下降,继而公平工资率w下降,最后带动L下降.~~当L>LN时,失业率仍保持为零,但这个过程终将使L0时,µ=0;F<100时,µ=0.121112−0.5−×+µ=,符合µ≥0.此时效用之和为52.若F1=0,那么有0.25200101若F1=100,那么有15−µ2=0,符合µ2≥0,此时效用之和为15.若04⎪0,p>6解:市场需求曲线为⎩Y,结合供给曲线,得到pY=6,消费量为6.价格与B的消费数量相同,但A消费数量为零.8改革开放以来各地区的工业发展对我国经济的持续高速发展做出了很大的贡献,然而也造成了日益加重的环境污染.试根据经济学原理讨论下列问题.8.1环境污染为什么通常难以由污染者自行解决,而需要政府加以管理?答:因为如果由市场机制决定污染量,交易成本高昂;因此需要政府加以关系.8.2解决环境污染的常用办法为:关闭工厂,制定排污标准并对超标者罚款,按照污染物排放量收费.试从经济学角度分析比较这三种方法.答:优劣由三个方面的成本来决定.工厂产品的盈利前景;污染的社会成本;以及交易成本.如果后两者相加大于前者,那么工厂应当关闭;如果后两者小于前者,那么,制定排污标准,信息与执行成本较小,但污染的社会成本会增加;而按照污染排放量,信息与执行成本较高,但污染的社会成本较小.9判断下列说法是否正确,并给出理由.在完全竞争市场条件下,如果对商品的生产增加税收,则增税的负担主要落在生产者头上,如果对商品的销售增加税收,则增税的负担主要落在消费者头上.答:在短期,负担在生产者和消费者头上;在长期,负担在消费者头上.但是否在生产和销售上增税,与税负的分担无关.10你认为下列物品中哪些属于公共品?那些属于私人品?为什么?注:这里我的答案拿不准,仅供参考.10.1自然环境保护区如果是指划成自然环境保护的区域.具有排他性,因为并非处处都是自然保护区.不具有竞争性,因为别人进入自然保护区并不能使另外的人不进去.如果是指“自然环境保护区”的称号;那么它是私人产品.10.2道路143
第十七讲外在性……纯公共产品.10.3进入索马里以拯救饥荒中的难民如果指援救服务,则是私人产品.10.4公共电视节目纯公共产品.10.5闭路电视节目私人产品.u0.50.5it(x,x)=e=xx,即为典型的柯布‒道格拉更直观地,作u(x1,x2)的单调变换,令1211斯函数形式,具有所有“良好性状的(well-behaved)偏好”的所有特征,当然这些特征中包括边际效用递减.(“良好性状”语出范里安《现代观点》第三章.)ii我认为该小问需要补充α1+α2=1才能得证,否则只能证明偏好关系的趋近关系.在解答中可以看出来,如果α1+α2≠1,题目中的效用函数的极限不存在.考研咨询版上网友的回答是平老师从原题上漏掉的.iii这个间接效用函数揭示的是完全互补型的偏好.在这样的偏好下,所有商品的消费量都是相等的.典型的情况就是鞋底跟鞋帮的关系.iv2001年原题.144'
您可能关注的文档
- 工程项目管理试题及答案-题库-自考用.doc
- 市场营销学第三版习题集及答案.doc
- 市场营销学练习及答案(吴健安).doc
- 希尔《国际商务》课后习题参考答案英文版.pdf
- 常俊林版《自动控制原理》课后习题解答.pdf
- 常州专业技术人员继续教育《沟通与协调能力》全部试题及答案.doc
- 常州专业技术人员继续教育《沟通与协调能力》题库-含答案.doc
- 常微分方程 习题答案.doc
- 常微分课后答案第五章.doc
- 平狄克《微观经济学》习题答案 (中文版).doc
- 平狄克《微观经济学》习题答案 [1].doc
- 平狄克《微观经济学》习题答案中文版.pdf
- 平狄克《微观经济学》课后答案 (中文版) 1-3章.doc
- 幼儿科学在线作业答案.doc
- 广东专插本《管理学》真题及答案(2001-2011).doc
- 广东农信网络学院柜员综合测试考试练习题答案汇总(可搜索查询答案版)doc.doc
- 广东海洋大学往年(2007—2013)《高等数学》期末考试试题10套集锦(含A,B卷与答案,完整版).pdf
- 广东省新版《初级会计电算化》考试理论复习题集含答案.doc