- 1.74 MB
- 2022-04-29 13:53:22 发布
- 1、本文档共5页,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,可选择认领,认领后既往收益都归您。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细先通过免费阅读内容等途径辨别内容交易风险。如存在严重挂羊头卖狗肉之情形,可联系本站下载客服投诉处理。
- 文档侵权举报电话:19940600175。
'《应用统计学》习题解答第一章绪论【1.1】指出下列变量的类型:(1)汽车销售量;(2)产品等级;(3)到某地出差乘坐的交通工具(汽车、轮船、飞机);(4)年龄;(5)性别;(6)对某种社会现象的看法(赞成、中立、反对)。【解】(1)数值型变量(2)顺序变量(3)分类变量(4)数值型变量(5)分类变量(6)顺序变量【1.2】某机构从某大学抽取200个大学生推断该校大学生的月平均消费水平。要求:(1)描述总体和样本。(2)指出参数和统计量。(3)这里涉及到的统计指标是什么?【解】(1)总体:某大学所有的大学生样本:从某大学抽取的200名大学生(2)参数:某大学大学生的月平均消费水平统计量:从某大学抽取的200名大学生的月平均消费水平(3)200名大学生的总消费,平均消费水平【1.3】下面是社会经济生活中常用的统计指标:①轿车生产总量,②旅游收入,③经济发展速度,④人口出生率,⑤安置再就业人数,⑥全国第三产业发展速度,⑦城镇居民人均可支配收入,⑧恩格尔系数。在这些指标中,哪些是数量指标,哪些是质量指标?如何区分质量指标与数量指标?【解】数量指标有:①、②、⑤质量指标有:③、④、⑥、⑦、⑧数量指标是说明事物的总规模、总水平或工作总量的指标,表现为绝对数的形式,并附有计量单位。而质量指标是说明总体相对规模、相对水平、工作质量和一般水平的统计指标,通常是两个有联系的统计指标对比的结果。【1.4】某调查机构从某小区随机地抽取了50为居民作为样本进行调查,其中60%的居民对自己的居住环境表示满意,70%的居民回答他们的月收入在6000元以下,生活压力大。回答以下问题:(1)这一研究的总体是什么?(2)月收入是分类变量、顺序变量还是数值型变量?(3)对居住环境的满意程度是什么变量?【解】(1)这一研究的总体是某小区的所有居民。-46-
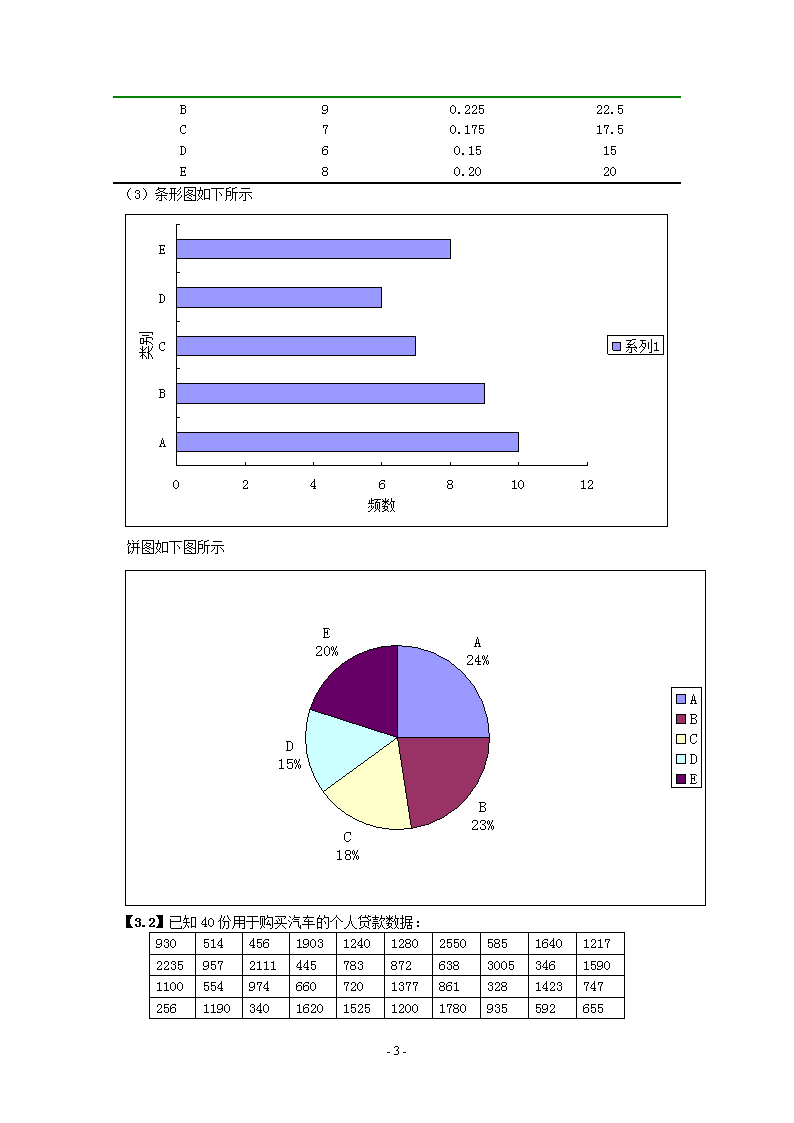
(2)月收入是数值型变量(3)对居住环境的满意程度是顺序变量。第二章统计数据的搜集【2.1】从统计调查对象包括的范围、调查登记时间是否连续、搜集资料的方法是否相同等方面,对以下统计调查实例分类,并指出各属于那种统计调查方式。(1)2004年,对我国的工业企业从业人数进行调查,各企业按上级部门要求填报统计表;(2)2004年,对全国所有第二、第三产业活动单位进行基本情况摸底调查,以2004年12月31日为标准时点,调查2004年度的资料;(3)对进口的一批产品,抽检其中少部分以对整批产品质量进行评价;(4)要了解全国粮食产量的基本情况,只要对全国几个重点粮食产区进行调查,就能及时地对全国粮食产量的基本情况进行推断;(5)为了探讨一项新改革措施实施的效果,推广其成功的经验,对已采取改革措施并产生明显效果的代表性单位进行调查。【解】(1)的调查方式是统计报表制度(2)的调查方式是普查(3)的调查方式是抽样调查(4)的调查方式是重点调查(5)的调查方式是典型调查【2.2】某调查机构从某小区随机地抽取了50位居民作为样本进行调查,其中60%的居民对自己的居住环境表示满意,70%的居民回答他们的月收入在6000元以下,生活压力大。回答下列的问题:(1)这里用到什么调查方式?(2)这里涉及的数据有哪些?哪些是截面数据,哪些是动态数据?【解】(1)这里用到的调查方式是抽样调查。(2)这里涉及的数据主要有:居民对居住环境的态度、月收入,这些数据都是截面数据。第三章统计数据的整理与显示【3.1】已知40名消费者购买5种不同款式的手机,分别是:A.诺基亚B.摩托罗拉C.波导D.联想E.西门子。他们购买的情况如下表所示:ABDBEBCDBABEDAAECEEDBEBADACAADEBECACCBAC要求:(1)指出上面的数据属于什么类型?(2)用Excel制作一张频数分布表。(3)绘制一张条形图和一张饼图,反映各类别的频数分布情况。【解】(1)上面数据属于分类型数据(2)频数分布表如下表所示:类别频数比例百分比(%)A100.2525-46-
B90.22522.5C70.17517.5D60.1515E80.2020(3)条形图如下所示饼图如下图所示【3.2】已知40份用于购买汽车的个人贷款数据:930514456190312401280255058516401217223595721114457838726383005346159011005549746607201377861328142374725611903401620152512001780935592655-46-
要求:(1)利用Excel的FREQUENCY函数进行统计分组整理,编制频数分布表,并计算出累积频数和累积频率。(2)利用SPSS绘制直方图。【解】(1)Excel中得到的频数分布表贷款数据频数频率(%)向上累积向下累积频数频率(%)频数频率(%)0~50061561540100500~10001640225534851000~1500820307518451500~2000615369010252000~25002538954102500以上254010025合计40100––––(2)SPSS中绘制的直方图【3.3】下表列出了最近某年5月15日美国30个城市的最低温度。要求做出最低温度数据的茎叶图。城市最低温度城市最低温度城市最低温度奥尔巴尼39哥伦比亚47洛杉矶61安克雷奇47哥伦布40孟菲斯51亚特兰大46达拉斯68纽约城50奥斯丁66底特律43菲克尼斯74-46-
伯明翰42韦恩堡37波特兰53波士顿53格林贝38旧金山55布法罗44檀香山65西雅图50卡斯帕51休斯顿67锡拉拉丘兹43芝加哥45杰克逊维尔50坦帕59克利夫兰40拉斯维加斯63华盛顿52【解】最低温度的茎叶图最低温度Stem-and-LeafPlotFrequencyStem&Leaf3.003.7896.004.0023344.004.56778.005.000112332.005.592.006.134.006.56781.007.4Stemwidth:10Eachleaf:1case(s)【3.4】下表列出了某班12名学生的身高、体重和肺活量的相关数据学生编号身高体重肺活量1135.132.01.752139.930.41.753163.646.22.754146.533.52.505156.237.12.756156.435.52.007167.841.52.758149.731.01.509145.033.02.5010148.537.22.2511165.549.53.0012135.027.61.25要求:绘制出不同学生的身高、体重和肺活量的箱线图。【解】12名学生身高、体重、肺活量的箱线图-46-
【3.5】据《中国统计年鉴.2005年》,1998~2004年中国对外贸易进出口数据如下:(单位:亿美元)年份1998199920002001200220032004出口总额1837194924922661325643825933进口总额1402165722512436295241285612要求:在同一坐标系内绘制出出口总额、进口总额的时间序列线图。【解】出口总额和进口总额的线图【3.6】从某一行业中随机抽取12家企业,所得产量与生产费用的数据如下:企业编号产量生产费用140130-46-
24215035015545514056515067815478416581001709116167101251801113017512140185要求:绘制产量与生产费用的散点图。【解】产量与生产费用之间的散点图第四章统计描述【4.1】某企业生产铝合金钢,计划年产量40万吨,实际年产量45万吨;计划降低成本5%,实际降低成本8%;计划劳动生产率提高8%,实际提高10%。试分别计算产量、成本、劳动生产率的计划完成程度。【解】产量的计划完成程度=即产量超额完成12.5%。成本的计划完成程=即成本超额完成3.16%。-46-
劳动生产率计划完=即劳动生产率超额完成1.85%。【4.2】某煤矿可采储量为200亿吨,计划在1991~1995年五年中开采全部储量的0.1%,在五年中,该矿实际开采原煤情况如下(单位:万吨)年份1991年1992年1993年1994年 1995年 上半年下半年上半年下半年实际开采量156230540279325470535累计开采量 试计算该煤矿原煤开采量五年计划完成程度及提前完成任务的时间。【解】本题采用累计法:(1)该煤矿原煤开采量五年计划完成==即:该煤矿原煤开采量的五年计划超额完成26.75%。(2)将1991年的实际开采量一直加到1995年上半年的实际开采量,结果为2000万吨,此时恰好等于五年的计划开采量,所以可知,提前半年完成计划。【4.3】我国1991年和1994年工业总产值资料如下表: 1991年1994年数值(亿元)比重(%)数值(亿元)比重(%)轻工业总产值13800.9 21670.6 重工业总产值14447.1 29682.4 工业总产值28248 51353 要求:(1)计算我国1991年和1994年轻工业总产值占工业总产值的比重,填入表中;(2)1991年、1994年轻工业与重工业之间是什么比例(用系数表示)?(3)假如工业总产值1994年计划比1991年增长45%,实际比计划多增长百分之几?【解】(1) 1991年1994年数值(亿元)比重(%)数值(亿元)比重(%)轻工业总产值13800.9 48.86%21670.6 42.20%重工业总产值14447.1 51.14%29682.4 57.8%-46-
工业总产值28248 ——51353 ——(2)是比例相对数;1991年轻工业与重工业之间的比例=;1994年轻工业与重工业之间的比例=(3)即,94年实际比计划增长25.37%。【4.4】某乡三个村2000年小麦播种面积与亩产量资料如下表:村名亩产量(斤)播种面积亩数(亩)所占比重(%)甲700120乙820150丙650130合计要求:(1)填上表中所缺数字;(2)用播种面积作权数,计算三个村小麦平均亩产量;(3)用比重作权数,计算三个村小麦平均亩产量。【解】(1)村名亩产量(斤)播种面积亩数(亩)所占比重(%)甲70012030%乙82015037.5%丙65013032.5%合计——400100%(2)(3)-46-
【4.5】两种不同品种的玉米分别在五块地上试种,产量资料如下:甲品种乙品种田块面积(亩)总产量(斤)田块面积(亩)总产量(斤)0.88400.96300.981011200111001.311701.110401.313001.212001.516805499065980已知生产条件相同,对这两种玉米品种进行分析比较,试计算并说明哪一种品种的亩产量更稳定一些?【解】即:由于是总体数据,所以计算总体均值:计算表格甲品种 田块面积(亩)总产量(斤)亩产量0.884010500.98109001110011001.11040945.451.212001000总计:54990—乙品种 田块面积(亩)总产量(斤)亩产量0.9630700-46-
1120012001.311709001.3130010001.516801120总计:65980—下面分别求两块田地亩产量的标准差:要比较两种不同玉米的亩产量的代表性,需要计算离散系数:,甲品种的亩产量更稳定一些。【4.6】两家企业生产相同的产品,每批产品的单位成本及产量比重资料如下:甲企业批次单位产品成本(元/台)产量比重(%)第一批10010第二批11020第三批12070合计——100乙企业批次单位产品成本(元/台)产量比重(%)第一批10033第二批11033第三批12034合计——100试比较两个企业哪个企业的产品平均单位成本低,为什么?【解】-46-
乙企业的产品平均单位成本更低。【4.7】某粮食储备库收购稻米的价格、数量及收购额资料如下:等级单价(元/斤)收购量(万斤)收购额(万元)一级品1.220002400二级品1.0530003150三级品0.940003600要求:(1)按加权算术平均数公式计算稻米的平均收购价格;(2)按加权调和平均数公式计算稻米的平均收购价格。【解】(1)(2)【4.8】已知我国1995年—1999年末总人口及人口增长率资料:年份199419951996199719981999年末总人口(万人)119850121121122389123626124810125909人口增长率(‰)11.610.4710.1110.19.588.81试计算该期间我国人口平均增长率。【解】计算过程如下:年份199419951996199719981999-46-
年末总人口(万人)119850121121122389123626124810125909年内总人口数(万人)——120486121755123008124218125360按照平均增长率的公式可知:所以,1995年—1999年期间我国人口平均增长率=‰【4.9】某单位职工按月工资额分组资料如下:按月工资额分组(元)职工人数(人)人数所占比重(%)4000元以下2510.594000-50003715.685000-600013456.786000-70003012.717000以上104.24总计236100.00根据资料回答问题并计算:(1)它是一个什么数列?(2)计算工资额的众数和中位数;(3)分别用职工人数和人数所占比重计算平均工资。结果一样吗?(4)分别计算工资的平均差和标准差。【解】(1)是等距分组数列(2)即:(注:用上限公式算出的结果与上述结果相同)-46-
(注:用上限公式算出的结果与上述结果相同)(3)两者结果一样。(忽略小数点位数的保留对结果造成的影响)(4)平均差标准差【4.10】某市甲、乙两商店把售货员按其人均年销售额分组,具体资料如下:甲商场乙商场按销售额分组(万元)售货员人数(人)按销售额分组(万元)售货员人数(人)20-303030-402030-4011040-508040-509050-605550-606060-704060以上1070以上5-46-
合计300合计200要求:(1)分别计算这两个商场售货员的人均销售额;(2)通过计算说明哪个商场人均销售额的代表性大?【解】(1)(2),乙商场销售额的代表性大。第五章统计抽样【5.1】袋中装有5只同样大小的球,编号为1,2,3,4,5,从中同时取出3只球,求取出的最大号的分布律及其分布函数并画出其图形。【解】先求的分布律:由题知,的可能取值为3,4,5,且-46-
,的分布律为:,由得:【5.2】设的密度函数为求:(1)常数c;(2)的分布函数;(3)。【解】(1)(2)当时,;当时,当时,.故分布函数(3)-46-
【5.3】随机变量相互独立,又,,试求和。【解】【5.4】一本书排版后一校时出现错误处数服从正态分布,求:(1)出现错误处数不超过230的概率;(2)出现错误处数在190~210的概率。【解】(1)(2)【5.5】某地区职工家庭的人均年收入平均为12000元,标准差为2000元。若知该地区家庭的人均年收入服从正态分布,现采用重复抽样从总体中随机抽取25户进行调查,问出现样本均值等于或超过12500元的可能性有多大?【解】对总体而言,样本均值【5.6】某商场推销一种洗发水。据统计,本年度购买此种洗发水的有10万人,其中3万6-46-
千人是女性。如果按重复抽样方法,从购买者中抽出100人进行调查,问样本中女性比例超过50%的可能性有多大?【解】总体比例即第六章统计推断【6.1】采取重复抽样的方法,从某总体中抽取样本容量为250的一组样本,已知样本成数(比例)p=0.38,试计算样本成数(比例)的估计误差及抽样标准差。【解】样本比例的估计误差为:抽样标准差为:【6.2】抽取一个样本容量为100的随机样本,其均值为36,标准差为7。试求总体均值95%的置信区间。【解】因为是大样本,总体方差未知,所以总体均值95%的置信区间为:【6.3】随机抽取一个由360名教师组成的样本,让每个人对一些说法表明自己的态度。第一种说法是“年龄偏大的学生对班上的讨论比年龄小的学生更积极”。态度按5分制来衡量:1=非常同意;2=同意;3=没有意见;4=不同意;5=很不同意。对这一看法,样本的平均态度得分为2.08,标准差为0.95。试用98%的置信度估计教师对这一看法的平均态度得分的置信区间。【解】因为是大样本,总体方差未知,所以总体均值的98%的置信区间为:-46-
【6.4】税务管理官员认为,大多数企业都有偷税漏税行为。在对由750个企业构成的随机样本的检查中,发现有121个企业有偷税漏税行为。试以90%的置信度估计偷税漏税企业比例的置信区间。【解】因为满足大样本,且样本比例为:所以,偷税漏税企业比例90%的置信区间为:【6.5】为估计自考学生的平均年龄,随机抽取一个样本容量为64的样本,其中平均年龄为26.5岁,标准差为4岁,试求自考学生总体平均年龄的99%的置信区间。【解】因为是大样本,总体方差未知,所以总体均值95%的置信区间为:【6.6】销售公司要求销售人员与顾客经常保持联系。一项由60名销售人员组成的随机样本表明:销售人员每周与顾客保持联系的平均次数为21.5次,样本标准差为4次。试求销售人员每周与顾客保持联系的总平均次数95%的置信区间。【解】因为是大样本,总体方差未知,所以总体均值95%的置信区间为:【6.7】某地区调查下岗职工中女性的比例,随机抽取了49名下岗职工,其中25人为女性,现以90%的置信度估计该地区下岗职工中女性比例的置信区间。【解】因为满足大样本,且样本比例为:所以,该地区下岗职工中女性比例的90%的置信区间为:【6.8】某健康机构想估计现代白领员工平均每天参加体育锻炼的时间。从16家公司中随机抽取25名白领员工,得知:其平均每天锻炼的时间为54分钟,标准差为30分钟。假设白领员工每天参加体育锻炼的时间服从正态分布。试求在95%的置信度下白领员工平均每天参加体育锻炼时间的置信区间。【解】因为是正态总体、小样本、方差未知所以,白领员工平均每天参加体育锻炼时间的95%的置信区间为:-46-
【6.9】某县城妇联要估计该地区职业女性平均每天的家务劳动时间,根据以往数据显示,该地区职业女性平均每天家务劳动时间的标准差为2小时。已知该地区的职业女性共有5000名,要求估计误差不超过1.5小时,假设采取不重复抽样,问:在95%的置信度下应该抽取多大的样本?【解】不重复抽样条件下,关于均值的样本量确定公式为:(注:将题目中的估计误差1.5小时改为0.5小时)【6.10】某省进行人口出生率的调查,根据以往的资料,该省的人口出生率约为10‰。若要求估计误差不超过5%,置信度为95%,在重复抽样条件下,应该抽取多大的样本?【解】重复抽样条件下,关于比例的样本量确定公式为:(注:将题目中的估计误差5%改为5‰)【6.11】设某厂生产的一种灯管的寿命,从过去较长一段时间的生产情况来看,灯管的平均寿命小时,现在采用新工艺后,在所生产的灯管中抽取36只,测得平均寿命小时,问采用新工艺后,灯管寿命是否有显著提高?()【解】根据题意,要检验采用新工艺后,灯管寿命是否有显著提高,因此采用单侧检验。建立的假设为:已知,,,,,因为是大样本,所以采用Z检验统计量。,因为,所以拒绝原假设,即采用新工艺后,灯管寿命有显著提高。【6.12】已知普通成年人安静时的心率服从正态分布,其平均数是72次/min。现从某体院随机抽测64名男生,测得安静时心率平均数为68次/min,标准差为6.4次/min,-46-
试问某体院男生安静时心率与普通成年人的心率有无差异?()【解】根据题意,要检验体院男生安静时心率与普通成年人的心率有无差异,即平均数是否达到72次/min,因此采用双侧检验。建立的假设为:已知,,,,,因为是大样本,所以采用Z检验统计量。,因为,所以拒绝原假设,即体院男生安静时心率与普通成年人的心率有差异。【6.13】某车间用一台包装机包装葡萄糖,包得的袋装糖重是一个随机变量,它服从正态分布。当机器正常时,其均值为0.5千克,标准差为0.015千克.某日开工后为检验包装机是否正常,随机地抽取它所包装的糖9袋,称得净重为(千克):0.4980.5080.5180.5240.4990.5130.5210.5150.512,问机器是否正常?()【解】根据题意,要检验机器是否正常工作,即袋装糖重是否为0.5千克,因此采用双侧检验。建立的假设为:已知,,,,因为是小样本,已知,所以采用Z检验统计量。,因为,所以拒绝原假设,即机器工作不正常。-46-
【6.14】四步助跑摸高成绩服从正态分布。我国女子优秀跳高运动员平均成绩为3.10米,某省6名女运动员的平均成绩为2.95米,标准差0.36米,问该省运动员的成绩是否低于我国优秀运动员?【解】根据题意,要检验该省运动员的成绩是否低于我国优秀运动员,因此采用单侧检验。建立的假设为:已知,,,,,因为是小样本,未知,所以采用检验统计量。,因为,所以不能拒绝原假设,即该省运动员的成绩不低于我国优秀运动员的成绩。【6.15】某厂家向一百货商店长期供应某种货物,双方根据厂家的传统生产水平,定出质量标准,即若次品率超过3%,则百货商店拒收该批货物。今有一批货物,随机抽43件检验,发现有次品2件,问应如何处理这批货物?【解】根据题意,要决定如何处理这批货物,也就是该百货商店要不要收这批货物,由次品率是否超过3%来决定,因此采用单侧检验。建立的假设为:已知,,,采用检验统计量。,因为,所以不能拒绝原假设,即百货商店可以接受这批货物。-46-
【6.16】某厂生产的某种型号电池,其寿命长期以来服从方差的正态分布。今有一批这种电池,从它的生产情况来看,寿命波动性比较大。为判断这种想法是否合乎实际,随机抽取了26只电池,测出其寿命的样本方差为。问根据这个数据能否判定这批电池的波动性较以往的有显著的变化(取)?【解】根据题意,要判定这批电池的波动性较以往是否有显著的变化,就是要检验这批电池的方差是否为5000,因为采用双侧检验。建立的假设为:已知,,,,采用检验统计量。,,因为,所以拒绝原假设,即这批电池的波动性较以往是有显著的变化。第七章方差分析(以下均为Excel输出结果)【7.1】有某种型号的电池,他们分别为甲、乙、丙三个工厂所生产的。为评比其质量,各随机抽取5只电池为样本,经试验测得其寿命(单位:小时)如下:试验号电池生产企业甲乙丙12345495039404328323026343840454248要求:检验三个工厂的电池平均寿命有无显著的差异?()-46-
【解】方差分析表差异源SSdfMSFP-valueFcrit组间604.93332302.466717.619420.0002693.885294组内2061217.16667总计810.933314 由于P-value=0.000269<0.05,说明拒绝原假设,表明三个工厂的电池平均寿命有显著差异。【7.2】某企业准备用三种方法组装一种新的产品,为确定哪种方法每小时生产的产品数量最多,随机抽取了20名工人,并指定每个人使用其中的一种方法。通过对每个工人生产的产品数进行方差分析得到下表的结果。差异源SSdfMSFP-valueFcrit组间4350.03253.592组内1904总计19要求:完成上面的方差分析表,并检验三种方法组装的产品数量之间是否有显著差异?()【解】差异源SSdfMSFP-valueFcrit组间87024353.81180.03253.592组内190417114.118总计19由于P-value=0.0325<0.05,说明拒绝原假设,表明三种方法组装的产品数量之间有显著差异。【7.3】为比较四种不同品牌的汽车使用相同类型汽油时的耗油量,在相同的行驶条件下,不同品牌汽车测得每加仑汽油所行使的里程数如下表:品牌1品牌2品牌3品牌4151214151211121391413111718161415-46-
要求:分析四种不同品牌的车耗油量是否有显著差异?()【解】方差分析表差异源SSdfMSFP-valueFcrit组间53.50098317.833667.1079480.0045233.410534组内32.61667132.508974总计86.1176516 由于P-value=0.004523<0.05,说明拒绝原假设,表明四种不同品牌的车耗油量之间有显著差异。【7.4】有4种不同的种子和5种不同施肥方案,在20块同样面积的土地上,分别用4种不同的种子和5种不同施肥方案搭配进行试验,取得的收获量数据见下表:品牌施肥方案12345112.013.010.49.711.4213.79.512.49.612.5314.311.511.311.110.9414.212.312.512.09.8要求:检验种子的不同品种对收获量的影响是否有显著差异?不同的施肥量方案对收获量的影响是否有显著差异?()【解】方差分析表差异源SSdfMSFP-valueFcrit行2.057530.6858330.4336140.7328513.490295列19.81244.9533.1315070.0557593.259167误差18.98121.581667总计40.849519 由于行因素的P-value=0.732851>0.05,说明不能拒绝原假设,表明没有证据证明不同品种的种子对收获量有显著的影响;由于列因素的P-value=0.055759>0.05,说明不能拒绝原假设,表明没有证据证明不同施肥量方案对收获量有显著的影响。【7.5】某金属材料生产过程中,为提高其强度,需要进行热处理。热处理的温度和时间是影响该材料强度的两个主要因素。现取三个温度水平和四个时间水平,各个不同水平的每一组合都进行了二次试验,测得该材料在各种热处理方式下的强度数据如下表。试分析温度、时间两个因素各自以及两个因素的交互作用对材料强度是否显著地影响。()-46-
时间BB1B2B3B4温度AA15356697163645659A27168777869705859A37576727168665658【解】方差分析差异源SSdfMSFP-valueFcrit样本256.08332128.041768.288892.78E-073.885294列714.79173238.2639127.07412.34E-093.490295交互313.5833652.2638927.874072.24E-062.99612内部22.5121.875总计1306.95823 由于行因素的P-value=2.78E-07<0.05,说明拒绝原假设,表明温度因素对材料强度有显著的影响;由于列因素的P-value=2.34E-09<0.05,说明拒绝原假设,表明时间因素对材料强度有显著的影响;交互作用的P-value=2.24E-06<0.05,说明拒绝原假设,表明温度和时间两个因素的交互作用对材料的强度有显著影响。第八章相关分析和回归分析*【8.1】某店主分析其店面的经营情况时,收集了连续10天的访问量数据(单位:天)和当天营业额数据(单位:元)如下。编号访问量营业额编号访问量营业额1741306739026610076670388130896140469110958505911601073100对以上访问量和营业额数据作相关分析。【解】相关分析(1)画访问量和营业额数据的散点图,如下所示-46-
从图上可以看出,访问量和营业额数据是简单线性正的不完全相关。(2)计算相关系数计算访问量和营业额的简单线性相关系数为0.871508,大于0.8,说明访问量和营业额之间存在较高的线性关系。【8.2】某饮料广告费投入为x,产品销售数量为y,根据收集2年的月度数据资料,计算得到以下结果:,,,(1)计算相关系数,并初步判断x与y之间的关系;(2)用最小二乘法估计模型回归系数,并写出模型结果;(3)说明所计算的回归系数的经济意义;(4)计算模型可决系数,并用其说明模型的拟合效果。【解】最小二乘法的计算(一元)(1)计算相关系数,并初步判断x与y之间的关系;计算x与y相关系数为r=0.996268,说明两者的简单线性相关程度非常高,因此可以初步判断x与y呈现线性关系。(2)用最小二乘法估计模型回归系数,并写出模型结果;记模型为:,将以上结果代入最小二乘法的计算公式,得到0.92484,151.1852。因此,产品销售数量为y对广告费投入为x的模型为(3)说明所计算的回归系数的经济意义;0.92484表示当广告费投入每增加1个单位,产品销售数量会增加0.92484个单位。(4)计算模型可决系数,并用其说明模型的拟合效果。由于模型为一元线性回归模型,根据一元线性回归模型中可决系数为模型因变量和自变量简单线性相关系数的平方的关系,可得模型的可决系数R2=(r)2=(0.996268)2=0.99255。可决系数接近1,说明模型拟合的非常好。【8.3】-46-
人们的收入期望往往受其教育程度和工作经验的影响,随机抽取了50名25-40岁之间的社会工作人员,收集了他们的月工资(单位:元)、受教育年限(单位:年,从小学开始计算,到最高学历为止,并扣除中间间断的时间)和工作年限(单位:年,按照毕业之后,开始工作时计算起)的数据,进行计算得到方差分析表和参数估计的结果如下所示。方差分析表误差来源dfSSMSFSignificanceF回归分析6703——残差————总计6745——————参数估计表变量系数标准误差t统计量Prob.受教育年限339.5722.2015.290.0000工作年限127.299.2313.790.0000常数项1278.7823.0355.520.0000要求:(1)根据参数估计表,说明收入期望与受教育程度和工作经验的关系;(2)根据参数估计表,说明受教育程度和工作经验对收入期望是否有显著影响;(2)完成以上方差分析表,对模型进行F检验;(3)计算模型的多重可决系数,并进行修正,说明模型的拟合效果。【解】最小二乘法的计算(多元)(1)根据参数估计表,说明收入期望与受教育程度和工作经验的关系;从参数估计表可以看出,收入期望(y)与受教育程度(x1)和工作经验(x2)模型为:该模型表示在受教育程度不变时,工作经验每增加1个单位,收入的期望会增加339.57个单位;在工作经验不变时,受教育程度每增加1个单位,收入的期望会增加127.29个单位。(2)根据参数估计表,说明受教育程度和工作经验对收入期望是否有显著影响;从参数估计表可以看出,受教育程度和工作经验的t统计量都大于2,说明受教育程度和工作经验对收入期望都是显著的。(2)完成以上方差分析表,对模型进行F检验;误差来源dfSSMSFSignificanceF回归分析267033351.53750.488——残差47420.8936————总计496745——————给定显著性水平查F统计量的表,3.195056,从方差分析表可以看出,F为3750.488,远远大于临界值,说明模型通过检验,认为模型整体是显著的,受教育程度和工作经验对收入期望有显著影响。(3)计算模型的多重可决系数,并进行修正,说明模型的拟合效果。从方差分析表中看出,模型解释的变差SSR=6703,模型的总变差SST=6745,所以模型的多重可决系数=0.993773。根据修正的多重可决系数=0.993508。模型多重可决系数和修正的多重可决系数均接近于1,说明模型拟合效果非常好。【8.4】-46-
国家财政收入来源于国民总收入。分析财政收入如何受国民总收入变化的影响,可以预测国家财政收入的规模,为国家的经济发展作规划。收集我国1990年到2010年的财政收入和国民总收入数据,如下表所示。我国1990年到2010年的财政收入和国民总收入数据表单位:亿元年份国民总收入X财政收入Y年份国民总收入X财政收入Y199018718.322937.102001108068.2216386.04199121826.203149.482002119095.6918903.64199226937.283483.372003135173.9821715.25199335260.024348.952004159586.7726396.47199448108.465218.102005183618.5131649.29199559810.536242.202006215883.9538760.20199670142.497407.992007266411.0251321.78199778060.858651.142008315274.7161330.35199883024.289875.952009341401.4868518.30199988479.1511444.082010403259.9683101.51200098000.4513395.23——————资料来源:《中国统计年鉴2011》试通过建立财政收入对国民总收入的一元线性回归模型来分析财政收入和国民总收入之间的关系。【解】一元线性回归模型(1)设定模型:记财政收入为y,国民总收入为x,设定财政收入对国民总收入的一元线性回归模型为。(2)使用Excel,根据最小二乘法得到以下估计的结果。根据以上结果,得到财政收入对国民总收入的一元线性回归模型为(3)模型检验根据Excel输出的结果,可以看到模型可决系数为0.991116098,非常接近于1,说明模型拟合很好。回归系数的t值分别为-6.821029和46.040199,绝对值都超过临界值,说明t检验通过,认为模型自变量对因变量的影响是显著的。模型的F值为211.6999,对应的p值为5.89*10-21-46-
,小于0.05,说明F检验通过,认为模型整体是显著的。(4)模型应用国民总收入X的回归系数为0.211980373,说明当国民总收入每增加1个单位,财政收入会增加0.211980373个单位。【8.5】消费问题是一个与我们的日常生活密切相关、大众普遍关注的问题。影响消费的因素有很多,主要的有收入和价格两大因素,分析消费受收入和价格影响的关系,是研究消费问题的基础。现研究某城镇居民耐用品的消费,收集其人均全年耐用消费品支出、人均年可支配收入和耐用消费品价格指数的统计资料如下表所示。年份人均耐用消费品支出Y(元)人均年可支配收入X1(元)耐用消费品价格指数X2(2000年=100)2000137.161181.4115.962001124.561375.7133.352002107.911501.2128.212003102.961700.6124.852004125.242026.6122.492005162.452577.4129.862006217.433496.2139.522007253.424283140.442008251.074838.9139.122009285.855160.3133.352010327.265425.1126.39利用表中数据,建立该城镇居民人均全年耐用消费品支出关于人均年可支配收入和耐用消费品价格指数的回归模型,进行回归分析。并检验人均年可支配收入及耐用消费品价格指数对城镇居民人均全年耐用消费品支出是否有显著影响。【解】多元线性回归模型(1)设定模型:设定人均全年耐用消费品支出关于人均年可支配收入和耐用消费品价格指数的二元线性回归模型为。(2)使用Excel,根据最小二乘法得到以下估计的结果。根据以上结果,得到人均全年耐用消费品支出关于人均年可支配收入和耐用消费品价格指数的二元线性回归模型为-46-
(3)模型t检验模型自变量X1的t值为10.5479,对应的p值为0.000,小于0.05,说明t检验通过,认为人均年可支配收入对人均全年耐用消费品支出的影响是显著的。自变量X2的t值为-0.9213,对应的p值为0.3838,大于0.05,说明t检验不通过,认为耐用消费品价格对人均全年耐用消费品支出的影响是不显著的。这与实际是吻合的。【8.6】经济学家菲利普斯在研究通货膨胀和就业问题时,发现经济体的通膨胀率和失业率往往存在一种交替关系的曲线:通货膨胀率高时,失业率低;通货膨胀率低时,失业率高。这就是著名的“菲利普斯曲线”。收集了某国物价上涨率P和失业率U的数据如下表所示。年份物价上涨率P(%)失业率U(%)年份物价上涨率P(%)失业率U(%)19860.62.819913.32.119870.12.819921.62.219880.72.519931.32.519892.32.319940.72.919903.12.11995-0.13.2根据以上数据,结合实际理论,建立P和U的回归模型,并进行检验分析。【解】非线性回归模型(1)画P和U的散点图,如下所示:结合以上散点图和经济学理论,可以看出,P与U成反向关系。因此,设定P与U的模型为:。(2)将U的数据做倒数变换,使用Excel,结合最小二乘法,得到模型的估计结果为:-46-
即P与U的模型为:(3)模型检验根据Excel输出的结果,可以看到模型可决系数为0.85542,大于0.8,说明模型拟合很好。回归系数的t值分别为-5.60915和6.879876,对应的P值都小于0.05,说明t检验通过,认为模型自变量对因变量的影响是显著的。模型的F值为47.33269,对应的p值为0.000127,小于0.05,说明F检验通过,认为模型整体是显著的。第九章统计指数【9.1】某市2008年第一季度社会商品零售额为36200万元,第四季度为35650万元,零售物价下跌0.5%。试计算该市社会商品零售额指数、零售价格指数和零售量指数以及由于零售物价下跌而使居民少支出的金额。【解】显然,零售额指数Kqp=;而零售价格指数Kp=100%-0.5%=99.5%;则零售量指数Kq=Kqp/Kp=98.48%/99.5%=98.98%;又因Kq=所以,,从而,由于零售物价下跌而使居民少支出的近额为:。【9.2】某市场上四种蔬菜的销售资料如下:品种销量(公斤)价格(元)销售额(元)-46-
基期报告期基期报告期基期假定报告期白菜5506001.601.808809609901080土豆2203002.001.90440600418570萝卜3203501.000.90320350288315番茄2452002.403.00588480735600合计13351450——2228239024312565(1)根据综合指数编制规则,将上表所缺空格填齐;(2)用拉氏公式编制四种蔬菜的销量总指数和价格总指数;(3)用帕氏公式编制四种蔬菜的销量总指数和价格总指数;(4)建立适当的指数体系,对蔬菜销售额的变动进行因素分析。【解】即计算表明:四种蔬菜的销量增长了7.27%,使销售额增加了162元;四种蔬菜的价格上长了7.32%,使销售额增加了175元;两因素共同影响,使销售额增长了15.12%,销售额增加了337元。结论:销售额销售量销售价格指数(%)115.12107.27107.32增幅(%)15.127.277.32增减额(元)337162175【9.3】某厂三种产品的产量情况如下表:产品计量单位出厂价格(元)产量基期报告期基期报告期ABC件个公斤81068.51151350011000400015000102004800试分析出厂价格和产量的变动对总产值的影响。【解】第一步:计算三个总产值:-46-
(万元);(万元);(万元);第二步:建立指标体系即第三步:分析结论。计算结果表明:由于出厂价上涨了3.64%,使总产值增加了8800元;由于产量提高了5.14%,使总产值增加了12900元;两因素共同作用,使总产值上升了8.97%,增加了21700元。【9.4】若给出【9.2】题中四种蔬菜的资料如下:品种个体价格指数销售额(元)%基期假定报告期白菜112.508801080土豆95.00440600418570萝卜90.00320350288315番茄125.00588480735600合计—2228239024312565(1)编制四种蔬菜的算术平均指数;(2)编制四种蔬菜的调和平均指数;(3)-46-
把它们与上题计算的拉氏指数和帕氏指数进行比较,看看有何种关系?什么条件下才会有这种关系的呢?【解】(1)(2)(3)算术平均指数的结果与拉氏指数相等——以基期的总值指标为权数。调和平均指数的结果与帕氏指数相等——以报告期的总值指标为权数。【9.5】某地区2005年农副产品收购总额为1360亿元,2006年比上年的收购总额增长了12%,农副产品价格指数为105%;试考虑:2006年与2005年相比较(1)农副产品收购总额增长了百分之几?农民共增加多少收入?(2)农副产品收购量增加了百分之几?农民增加了多少收入?(3)由于农副产品收购价格提高了5%,农民又增加了多少收入?(4)验证以上三者之间有何等关系?【解】已知:农民交售农副产品增加收入163.2亿元,与去年相比增长幅度为12%;农副产品收购数量增长6.67%,农民增加收入90.7亿元;农副产品收购价格上涨5.00%,农民增加收入72.5亿元。显然,有:-46-
可见,分析结论是协调一致的。【9.6】某公司下属三个生产某种产品的情况如下表:工厂类别单位产品成本(元)产量(吨)上月本月上月本月一厂二厂三厂9601010112095210151080465030001650493032002000根据上表数据计算可变构成指数、固定构成指数和结构影响指数,并分析单位成本水平和产量结构变动对总成本的影响。【解】(一)资料处理:计算五个指标——:计算结果见下表最后一行(红色数字):工厂类别单位产品成本(元)产量(吨)总成本(万元)上月x0本月x1上月f0本月f1基期f0x0假定f1x0报告期f1x1一厂二厂三厂9601010112095210151080465030001650493032002000446.0303.0184.8473.28323.20224.00469.36324.80216.00Σ————930010030933.81020.481010.16(二)计算三个指数:;固定构成指数;(三)建立指数体系:,即:-46-
(四)分析结论:计算结果表明,由于单位成本水平下降了1.01%(=1-98.99%),使得总成本减少了10元;由于产量结构改变了1.34%(=101.34%-1),使得总成本增加了13元;两个因素共同影响,使总成本上升了0.3%(=1003.0%-1),增加了3元。【9.7】某企业生产的三种产品的有关资料如下:产品产量增长率产量个体指数总成本(万元)%%基期假定报告期甲2512520.024.0乙4014045.06348.5丙4014035.04948.0合计——100.0137120.5(1)根据上表资料计算相关指标填入上表(见绿色区域数字);(2)计算产品产量总指数及由于产量增长而增加的总成本;(3)计算单位成本总指数及由于单位成本变动而增减的总成本。【解】建立指数体系:结论:总成本产品产量单位成本指数(%)120.50137.0087.96增幅(%)20.5037.00-12.04增减额(万元)20.537.0-16.5计算结果表明:由于产量总指数增加了37%(=137%-1),而使总成本增加了37元,由于单位成本总指数下降了12.04%(=87.96%-1),使总成本减少了16.5元。两个因素共同影响使总成本上升了20.5%,增加了20.5元。【9.8】某商场的销售资料如下:商品价格降低率价格个体指数销售额(万元)%%基期假定报告期甲1090117110乙595150136.84130丙1585187188.24160合计——454447.30400(1)根据上表资料计算相关指标填入上表(见绿色区域数字);-46-
(1)计算商品销售量总指数及由于销量变化而增减的销售额;(2)计算商品价格总指数及由于价格变动而增减的销售额。【解】建立指数体系:销售额销售量销售价格指数(%)88.1198.5289.43增幅(%)增减额(万元)计算结果表明:由于商品销量总指数下降了1.48%(=1-98.52%),而使销售额减少了6.7万元,由于商品价格总指数下降了10.57%(=1-89.43%),使销售额减少了47.3万元。两个因素共同影响使销售总额下降了11.89%(=1-88.11%),减少了54万元。【9.9】某城市三个市场上同一商品的有关资料如下:市场销售量(公斤)价格(元)销售额(元)基期报告期基期报告期基期假定报告期A7405602.503.00185014001680B6707102.402.80160817041988C5508202.202.40121018041968合计19602090——466849085636(1)编制该商品平均价格的可变构成指数、结构影响指数和固定构成指数;(2)建立指数体系,从相对数的角度进行平均价格变动的因素分析。(3)进一步,综合分析销售量变动和价格变动对该商品销售额的影响。【解】(1)因为所以,可变构成指数:结构影响指数:固定构成指数:(2)指数体系:计算表明:由于商品销售结构的变化,使得其平均价格下降了1.4%-46-
(=1-98.60%);由于各商品市场价格水平的变化,使得其平均价格上涨了14.83%(=114.83%-1)(3)综合分析销售总额的变动影响:因为:即即所以,计算结果表明:由于销售量上升了6.63%(=106.63%-1),使得销售额增加了309.61元;由于价格水平上涨了13.23%(=113.23%-1),使得销售额增加了658.39元;两个因素共同影响,是销售总额上升了20.74%,增加了968元。【9.10】某乡力图通过推广良种和改善田间耕作管理来提高粮食生产水平,有关生产情况如下表所示:粮食品种播种面积(亩)亩产(公斤/亩)总产量(万公斤)基期报告期基期报告期基期假定报告期A38000690004204321596.02898.02980.8B46000420003953981817.01659.01671.6C3600090003433571234.8308.7321.3合计120000120000——4647.84865.74973.7(1)该乡粮食平均亩产提高了百分之几?由此增产粮食多少吨?(2)改善田间耕作管理使平均亩产提高多少?增产粮食多少吨?(3)推广良种使平均亩产提高多少?增产粮食多少吨?【解】计算的相关数据()见上表中绿色区域数字;从而有:建立指数体系:-46-
即即分析结论:计算结果表明(1)该乡粮食平均亩产提高了7.01%(=107.01%-1),由此增产粮食3259吨;(2)由于改善田间管理,使平均亩产提高了4.69%,粮食增产2179吨;(3)由于推广优良品种,使平均亩产提高了2.22%,粮食增产1080吨。第十章时间序列分析【10.1】某公司2009年末有职工250人,10月上旬的人数变动情况是:10月4日新招聘12名大学生上岗,6日有4名老职工退休离岗,8日有3名青年职工应征入伍,同日又有3名职工辞职离岗,9日招聘7名销售人员上岗。试计算该公司10月上旬的平均在岗人数。【解】答:该公司10月上旬的平均在岗人数为256人。【10.2】某银行2009年部分月份的现金库存额资料如下:日期1月1日2月1日3月1日4月1日5月1日6月1日7月1日库存额(万元)500480450520550600580要求:(1)该时间序列属于哪一种时间序列?.(2)分别计算该银行该年第一、二季度和上半年的平均现金库存额。【解】(1)该时间序列属于动态时点时间序列;(2)第一季度平均现金库存额:;第二季度平均现金库存额:;上半年平均现金库存额:-46-
【10.3】某企业08年上半年的产量和单位成本资料如下:月份123456产量(件)单位成本(元)200073300072400071300073400069500068试计算该企业08年上半年的产品平均单位成本。【解】答:该企业08年上半年的产品平均单位成本为70.5元。【10.4】某企业有关资料如下,计算该企业一季度人均月销售额。月份一二三四销售额(万元)100150120140月初职工数(人)100120110116【解】该企业一季度月平均销售额:;该企业一季度月平均职工人数:;该企业一季度人均月销售额:。【10.5】填写下表,保留到整数:年份产量累积增长量定基发展速度环比发展速度增长1%绝对值(万吨)(万吨)(%)(%)(百吨)20017142————200235282003181.812004105.272005106.2820068286-46-
【解】根据已知数据条件,分别利用累积增长量、定基发展速度、环比发展速度和增长1%绝对值等计算公式计算相应数据填写上表(见表中绿色区域数字)【10.6】某市2001~2005年的地区生产总值如下表:年份20012002200320042005GDP(亿元)9931123127014371626(1)按平均发展速度估计2002~2004年的地区生产总值。(2)按此5年的平均发展速度预测2008年和2010年的GDP。【解】(1)2002~2006年泉州市地区生产总值的平均发展速度为:;按平均发展速度估计2002~2004年的地区生产总值分别为:(将计算结果填入上表绿色区域内);(2)按此5年的平均发展速度预测2008年和2010年的GDP分别为:2008年地区GDP预测值;2010年地区GDP预测值。【10.7】我国某地区2001年~2006年税收总额如下:年份200120022003200420052006税收收入(亿元)282129903296425551266038试计算:(1)环比发展速度和定基发展速度;(2)环比增长速度和定基增长速度;(3)增长1%绝对值;(4)用水平法计算平均增长速度;(5)分析表中所列资料反映的趋势特征,拟配合适的趋势模型,并预测2007年该地区的税收收入。【解】(1)~(3)相关计算结果填入下表(见绿色区域数字):年份200120022003200420052006税收收入(亿元)282129903296425551266038发展速度(%)环比—105.99110.23129.10120.47117.79定基—105.99116.84150.83180.71214.04增长速度(%)环比—5.9910.2329.1020.4717.79定基—5.9916.8450.8380.71114.02增长1%的绝对值(百万元)—28212990329642555126(4)用水平法计算平均发展速度和平均增长速度:-46-
平均发展速度;则平均增长速度;(5)分析表中所列资料反映的趋势特征,拟配合适的趋势模型,并预测2007年该地区的税收收入。年份时间税收收入ty2001-5282125-14105——2412.52002-329909-89701963082.62003-132961-32963063752.7200414255142559594422.72005351269153789715092.820065603825301909125762.9合计0245267023452——24526根据上表时间数列的各项数据计算其逐期增长量Δу,由于从04年开始Δу基本在910至970亿元之间波动,因此,其发展趋势是直线型,故应建立直线趋势方程式。采用简捷法求解a、b参数,将表中相关数据代入计算公式计算得:;得趋势直线方程:。该方程反映了该地区2001——2006年税收收入的发展趋势。依次将表中的年序号t值代入上述方程,可求得各年的趋势值yc(见表中最后一列数字)所以,2007年该地区税收收入的预测值为:(亿元)。由上表可以看出,各年税收收入实际值(y)总和与趋势值(yc)总和是相等的。即:。第十一章企业经济统计概述【11.1】某微型食品加工厂某月工业生产成果及费用资料如下表所示(单位:万元):项目金额项目金额外购燃料2.4企业产品产值165.5外购动力1.2提取的职工福利基金2.6外购材料11.5生产税净额12工资30营业盈余80固定资产折旧14.4其他支出10利息支出1.4-46-
试分别用生产法和分配法计算企业产品增加值。【解】生产法:总产值—中间投入(消耗)=165.5—2.4—1.2—11.5—1.4—10=139(万元);分配法:14.4+30+2.6+80+12=139(万元)。某厂一月份的销售资料如下:单位(万元)指标金额产品销售收入400产品销售成本200企业其他业务收入30产成品期末期初差额(历史成本)70在成品期末期初差额(历史成本)30会计账面应交增殖税6试计算该企业的产品产值。【11.2】某厂一月份的销售资料如下:单位(万元)指标金额产品销售收入400产品销售成本200企业其他业务收入30产成品期末期初差额(历史成本)70在成品期末期初差额(历史成本)30会计账面应交增殖税6计算该企业的产品产值。【解】根据书本上关于工业企业总产值的计算方法:全部产品应交增值税=[(70+30)*400/200+400]*6/400=9(万元);企业的产品产值=400+(70+30)*400/200+30+9=639(万元)。根据下表给出的电力企业有关数据,计算该企业的投入产出综合评价指数。核算基础具体指标实际指标值社会最好值权数以活劳动投入为基础企业全员劳动生产率(元/人)200025000.17企业职工工资产值率(元/百元)500050000.10以劳动手段投入为基础生产设备综合利用率(%)89950.15固定资产企业营业盈余率(元/百元)2402500.1以劳动对象投入为基础单位原材料、燃料消耗总产出(元/百元)3003200.1企业流动资产周转次数(次)580.08以成本费用投入为基础成本利税率(%)43450.17资金利税率(%)39420.13【11.3】根据下表给出的某电力企业有关数据,计算该企业的投入产出综合评价指数。核算基础具体指标实际指标值社会最好值权数-46-
以活劳动投入为基础企业全员劳动生产率(元/人)200025000.17企业职工工资产值率(元/百元)500050000.10以劳动手段投入为基础生产设备综合利用率(%)89950.15固定资产企业营业盈余率(元/百元)2402500.1以劳动对象投入为基础单位原材料、燃料消耗总产出(元/百元)3003200.1企业流动资产周转次数(次)580.08以成本费用投入为基础成本利税率(%)43450.17资金利税率(%)39420.13【解】从上表可得:各指标的单项指数ki=实际指标值/社会最好值投入产出能力综合评价指数为1时,是最好。该企业实际为0.901,可认为该企业投入产出能力指数较接近1,属于企业投入产出较好的企业。第十二章国民经济统计概述【12.1】现有某地区2011年国民经济核算有关资料:总产出11143.49亿元,中间消耗7930.68亿元,固定资产折旧524.06亿元,劳动者报酬1427.73亿元,生产税净额420.60亿元,营业盈余834.32亿元,农村居民消费147.71亿元,城镇居民消费901.80亿元,政府消费650.60亿元,固定资本形成1913.12亿元,存货增加96.90亿元,货物和服务净出口-497.12亿元。试用生产法、收入法、支出法计算该地区2011年国内生产总值。【解】用生产法核算GDP:GDP=总产出-中间消耗=11143.49-7930.68=3212.81(万元);用收入法核算GDP:GDP=劳动者报酬+生产税净额+固定资产折旧+营业盈余=1427.73+420.60+524.06+834.32=3206.71(万元);用支出法核算GDP:GDP=最终消费+资本形成+净出口=(147.71+901.80+650.60)+(1913.12+96.90)-497.12=3213.01(万元)。(以上三种方法核算结果存在一定的误差。)【12.2】请将正确答案的字母填入空白处:投入产出表中,第二产业行与第一产业列交叉项的数值,从横向上看表示_______,从列向上看表示_______。A.第二产业部门在生产过程中消耗第一产业部门的产品数量-46-
B.第二产业部门的产品提供给第一产业部门作为生产消耗使用的数量C.第一产业部门在生产过程中消耗第二产业部门的产品数量D.第一产业部门的产品提供给第二产业部门作为生产消耗使用的数量【解】BC【12.3】已知企业增加值280亿元,支付劳动报酬170亿元,支付生产税10亿元,政府生产补贴2亿元,国库券的利息收入3亿元,支付财产收入(包括分红、利息等)20亿元,上缴政府所得税30亿元,补贴医疗、食堂、学校等非物质生产部门5亿元,支援灾区捐款0.1亿元。试计算该企业的原始收入和可支配收入。【解】企业的原始收入=280-170-10+2+3-20=85(亿元)企业的可支配收入=原始收入+转移性净收入=85-30-5-0.1=49.9(亿元)【12.4】某国期初资产规模为1400亿美元。当期新增固定资产350亿美元,存货减少了150亿美元,新发现勘探可采石油储量价值70亿美元,与某一国外政府签订的20亿美元贷款到期因政治原因无需偿还。此外,由于台风给该国各部门共带来了10亿美元的资产损失,由于全球经济的发展,到期末时,期初资产价格增加了10%,另全年资产折旧和退役共100亿美元。根据上述材料,试计算该国期末的资产价值。【解】期末资产=期初资产+期间资产的变动=1400*(1+10%)+350-150+70+20-10-100=1720(亿美元)-46-'
您可能关注的文档
- 广西2016年专业技术人员继续教育公需科目《专业技术人员创新与创业能力建设》考试题目与答案.doc
- 广西《生态文明与可持续发展》公需科目考题及答案库.doc
- 广西工学院《计算机系统结构》习题及答案(15页,有题有答案).doc
- 应用文写作习题及答案.doc
- 作教材_第2版_习题答案.pdf
- 应用概率统计课后习题答案详解.doc
- 应用物理化学习题解答.doc
- 应用经济学专业《微观经济学》练习册参考答案.docx
- 应用经济学课后习题答案.doc
- 底盘习题答案.doc
- 庞浩版计量经济学课后习题答案.doc
- 廖常初《FX系列PLC编程及应用》课后习题答案.pdf
- 廖承恩《微波技术基础》第四,第六章答案.doc
- 建筑CAD_习题集(含答案).doc
- 建筑力学及课后答案解析(1).doc
- 建筑安全《1200问》考题及答案.doc
- 建筑工程概预算练习题及答案(已整理).doc
- 建筑工程概预算练习题及答案2013.doc