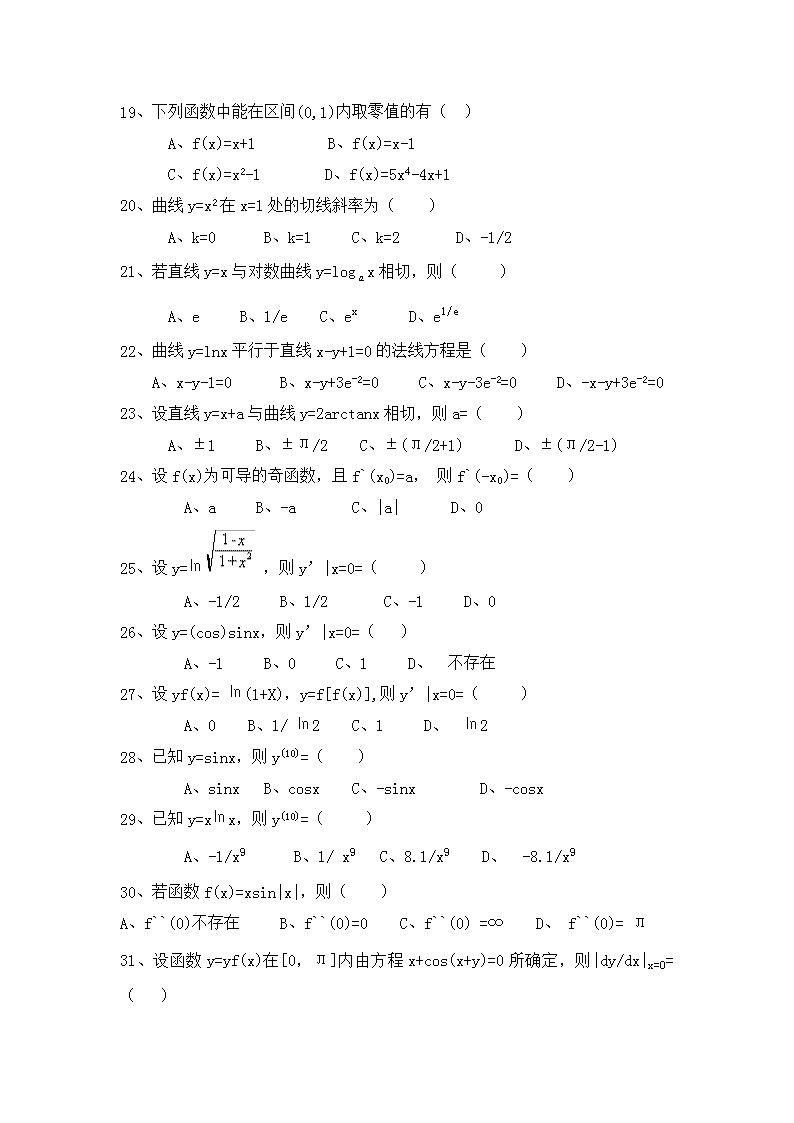- 397.50 KB
- 2022-04-29 13:53:20 发布
- 1、本文档共5页,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,可选择认领,认领后既往收益都归您。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细先通过免费阅读内容等途径辨别内容交易风险。如存在严重挂羊头卖狗肉之情形,可联系本站下载客服投诉处理。
- 文档侵权举报电话:19940600175。
'《高等数学》练习测试题库及答案一.选择题1.函数y=是()A.偶函数B.奇函数C单调函数D无界函数2.设f(sin)=cosx+1,则f(x)为()A2x-2B2-2xC1+xD1-x3.下列数列为单调递增数列的有()A.0.9,0.99,0.999,0.9999B.,,,C.{f(n)},其中f(n)=D.{}4.数列有界是数列收敛的()A.充分条件B.必要条件C.充要条件D既非充分也非必要5.下列命题正确的是()A.发散数列必无界B.两无界数列之和必无界C.两发散数列之和必发散D.两收敛数列之和必收敛6.()A.1B.0C.2D.1/27.设e则k=()A.1B.2C.6D.1/68.当x1时,下列与无穷小(x-1)等价的无穷小是()A.x-1B.x-1C.(x-1)D.sin(x-1)9.f(x)在点x=x0处有定义是f(x)在x=x0处连续的()A.必要条件B.充分条件C.充分必要条件D.无关条件10、当|x|<1时,y=()A、是连续的B、无界函数C、有最大值与最小值D、无最小值
11、设函数f(x)=(1-x)cotx要使f(x)在点:x=0连续,则应补充定义f(0)为()A、B、eC、-eD、-e-112、下列有跳跃间断点x=0的函数为()A、xarctan1/xB、arctan1/xC、tan1/xD、cos1/x13、设f(x)在点x0连续,g(x)在点x0不连续,则下列结论成立是()A、f(x)+g(x)在点x0必不连续B、f(x)×g(x)在点x0必不连续须有C、复合函数f[g(x)]在点x0必不连续D、在点x0必不连续14、设f(x)=在区间(-∞,+∞)上连续,且f(x)=0,则a,b满足()A、a>0,b>0B、a>0,b<0C、a<0,b>0D、a<0,b<015、若函数f(x)在点x0连续,则下列复合函数在x0也连续的有()A、B、C、tan[f(x)]D、f[f(x)]16、函数f(x)=tanx能取最小最大值的区间是下列区间中的()A、[0,л]B、(0,л)C、[-л/4,л/4]D、(-л/4,л/4)17、在闭区间[a,b]上连续是函数f(x)有界的()A、充分条件B、必要条件C、充要条件D、无关条件18、f(a)f(b)<0是在[a,b]上连续的函f(x)数在(a,b)内取零值的()A、充分条件B、必要条件C、充要条件D、无关条件
19、下列函数中能在区间(0,1)内取零值的有()A、f(x)=x+1B、f(x)=x-1C、f(x)=x2-1D、f(x)=5x4-4x+120、曲线y=x2在x=1处的切线斜率为()A、k=0B、k=1C、k=2D、-1/221、若直线y=x与对数曲线y=logx相切,则()A、eB、1/eC、exD、e1/e22、曲线y=lnx平行于直线x-y+1=0的法线方程是()A、x-y-1=0B、x-y+3e-2=0C、x-y-3e-2=0D、-x-y+3e-2=023、设直线y=x+a与曲线y=2arctanx相切,则a=()A、±1B、±л/2C、±(л/2+1)D、±(л/2-1)24、设f(x)为可导的奇函数,且f`(x0)=a,则f`(-x0)=()A、aB、-aC、|a|D、025、设y=㏑,则y’|x=0=()A、-1/2B、1/2C、-1D、026、设y=(cos)sinx,则y’|x=0=()A、-1B、0C、1D、不存在27、设yf(x)=㏑(1+X),y=f[f(x)],则y’|x=0=()A、0B、1/㏑2C、1D、㏑228、已知y=sinx,则y(10)=()A、sinxB、cosxC、-sinxD、-cosx29、已知y=x㏑x,则y(10)=()A、-1/x9B、1/x9C、8.1/x9D、-8.1/x930、若函数f(x)=xsin|x|,则()A、f``(0)不存在B、f``(0)=0C、f``(0)=∞D、f``(0)=л31、设函数y=yf(x)在[0,л]内由方程x+cos(x+y)=0所确定,则|dy/dx|x=0=()
A、-1B、0C、л/2D、232、圆x2cosθ,y=2sinθ上相应于θ=л/4处的切线斜率,K=()A、-1B、0C、1D、233、函数f(x)在点x0连续是函数f(x)在x0可微的()A、充分条件B、必要条件C、充要条件D、无关条件34、函数f(x)在点x0可导是函数f(x)在x0可微的()A、充分条件B、必要条件C、充要条件D、无关条件35、函数f(x)=|x|在x=0的微分是()A、0B、-dxC、dxD、不存在36、极限的未定式类型是()A、0/0型B、∞/∞型C、∞-∞D、∞型37、极限的未定式类型是()A、00型B、0/0型C、1∞型D、∞0型38、极限=()A、0B、1C、2D、不存在39、xx0时,n阶泰勒公式的余项Rn(x)是较xx0的()A、(n+1)阶无穷小B、n阶无穷小C、同阶无穷小D、高阶无穷小40、若函数f(x)在[0,+∞]内可导,且f`(x)>0,xf(0)<0则f(x)在[0,+∞]内有()A、唯一的零点B、至少存在有一个零点C、没有零点D、不能确定有无零点
41、曲线y=x2-4x+3的顶点处的曲率为()A、2B、1/2C、1D、042、抛物线y=4x-x2在它的顶点处的曲率半径为()A、0B、1/2C、1D、243、若函数f(x)在(a,b)内存在原函数,则原函数有()A、一个B、两个C、无穷多个D、都不对44、若∫f(x)dx=2ex/2+C=()A、2ex/2B、4ex/2C、ex/2+CD、ex/245、∫xe-xdx=(D)A、xe-x-e-x+CB、-xe-x+e-x+CC、xe-x+e-x+CD、-xe-x-e-x+C46、设P(X)为多项式,为自然数,则∫P(x)(x-1)-ndx()A、不含有对数函数B、含有反三角函数C、一定是初等函数D、一定是有理函数47、∫-10|3x+1|dx=()A、5/6B、1/2C、-1/2D、148、两椭圆曲线x2/4+y2=1及(x-1)2/9+y2/4=1之间所围的平面图形面积等于()A、лB、2лC、4лD、6л49、曲线y=x2-2x与x轴所围平面图形绕轴旋转而成的旋转体体积是()A、лB、6л/15C、16л/15D、32л/1550、点(1,0,-1)与(0,-1,1)之间的距离为()A、B、2C、31/2D、21/251、设曲面方程(P,Q)则用下列平面去截曲面,截线为抛物线的平面是()A、Z=4B、Z=0C、Z=-2D、x=252、平面x=a截曲面x2/a2+y2/b2-z2/c2=1所得截线为()A、椭圆B、双曲线C、抛物线D、两相交直线53、方程=0所表示的图形为()A、原点(0,0,0)B、三坐标轴
C、三坐标轴D、曲面,但不可能为平面54、方程3x2+3y2-z2=0表示旋转曲面,它的旋转轴是()A、X轴B、Y轴C、Z轴D、任一条直线55、方程3x2-y2-2z2=1所确定的曲面是()A、双叶双曲面B、单叶双曲面C、椭圆抛物面D、圆锥曲面二、填空题1、求极限(x2+2x+5)/(x2+1)=()2、求极限[(x3-3x+1)/(x-4)+1]=()3、求极限x-2/(x+2)1/2=()4、求极限[x/(x+1)]x=()5、求极限(1-x)1/x=()6、已知y=sinx-cosx,求y`|x=л/6=()7、已知ρ=ψsinψ+cosψ/2,求dρ/dψ|ψ=л/6=()8、已知f(x)=3/5x+x2/5,求f`(0)=()9、设直线y=x+a与曲线y=2arctanx相切,则a=()10、函数y=x2-2x+3的极值是y(1)=()11、函数y=2x3极小值与极大值分别是()12、函数y=x2-2x-1的最小值为()13、函数y=2x-5x2的最大值为()14、函数f(x)=x2e-x在[-1,1]上的最小值为()15、点(0,1)是曲线y=ax3+bx2+c的拐点,则有b=()c=()16、∫xx1/2dx=()17、若F`(x)=f(x),则∫dF(x)=()18、若∫f(x)dx=x2e2x+c,则f(x)=()19、d/dx∫abarctantdt=()
20、已知函数f(x)=在点x=0连续,则a=()21、∫02(x2+1/x4)dx=()22、∫49x1/2(1+x1/2)dx=()23、∫031/2adx/(a2+x2)=()24、∫01dx/(4-x2)1/2=()25、∫л/3лsin(л/3+x)dx=()26、∫49x1/2(1+x1/2)dx=()27、∫49x1/2(1+x1/2)dx=()28、∫49x1/2(1+x1/2)dx=()29、∫49x1/2(1+x1/2)dx=()30、∫49x1/2(1+x1/2)dx=()31、∫49x1/2(1+x1/2)dx=()32、∫49x1/2(1+x1/2)dx=()33、满足不等式|x-2|<1的X所在区间为()34、设f(x)=[x]+1,则f(л+10)=()35、函数Y=|sinx|的周期是()36、y=sinx,y=cosx直线x=0,x=л/2所围成的面积是()37、y=3-2x-x2与x轴所围成图形的面积是()38、心形线r=a(1+cosθ)的全长为()39、三点(1,1,2),(-1,1,2),(0,0,2)构成的三角形为()40、一动点与两定点(2,3,1)和(4,5,6)等距离,则该点的轨迹方程是()41、求过点(3,0,-1),且与平面3x-7y+5z-12=0平行的平面方程是()42、求三平面x+3y+z=1,2x-y-z=0,-x+2y+2z=0的交点是()43、求平行于xoz面且经过(2,-5,3)的平面方程是()
44、通过Z轴和点(-3,1,-2)的平面方程是()45、平行于X轴且经过两点(4,0,-2)和(5,1,7)的平面方程是()三、解答题1、设Y=2X-5X2,问X等于多少时Y最大?并求出其最大值。2、求函数y=x2-54/x.(x<0=的最小值。3、求抛物线y=x2-4x+3在其顶点处的曲率半径。4、相对数函数y=㏑x上哪一点处的曲线半径最小?求出该点处的曲率半径。5、求y=x2与直线y=x及y=2x所围图形的面积。6、求y=ex,y=e-x与直线x=1所围图形的面积。7、求过(1,1,-1),(-2,-2,2)和(1,-1,2)三点的平面方程。8、求过点(4,-1,3)且平行于直线(x-3)/2=y=(z-1)/5的直线方程。9、求点(-1,2,0)在平面x+2y-z+1=0上的投影。10、求曲线y=sinx,y=cosx直线x=0,x=л/2所围图形的面积。11、求曲线y=3-2x-x2与x轴所围图形的面积。12、求曲线y2=4(x-1)与y2=4(2-x)所围图形的面积。13、求抛物线y=-x2+4x-3及其在点(0,3)和(3,0)得的切线所围成的图形的面积。9/414、求对数螺线r=eaθ及射线θ=-л,θ=л所围成的图形的面积。15、求位于曲线y=ex下方,该曲线过原点的切线的左方以及x轴上方之间的图形的面积。16、求由抛物线y2=4ax与过焦点的弦所围成的图形面积的最小值。17、求曲线y=x2与x=y2绕y轴旋转所产生旋转体的体积。18、求曲线y=achx/a,x=0,y=0,绕x轴所产生旋转体的体积。19、求曲线x2+(y-5)2=16绕x轴所产生旋转体的体积。20、求x2+y2=a2,绕x=-b,旋转所成旋转体的体积。21、求椭圆x2/4+y2/6=1绕轴旋转所得旋转体的体积。22、摆线x=a(t-sint),y=a(1-cost)的一拱,y=0所围图形绕y=2a(a>0)旋转所得旋转体体积。
23、计算曲线上相应于的一段弧的长度。24、计算曲线y=x/3(3-x)上相应于1≤x≤3的一段弧的长度。25、计算半立方抛物线y2=2/3(x-1)3被抛物线y2=x/3截得的一段弧的长度。26、计算抛物线y2=2px从顶点到这典线上的一点M(x,y)的弧长。27、求对数螺线r=eaθ自θ=0到θ=ψ的一段弧长。28、求曲线rθ=1自θ=3/4至θ4/3的一段弧长。29、求心形线r=a(1+cosθ)的全长。30、求点M(4,-3,5)与原点的距离。31、在yoz平面上,求与三已知点A(3,1,2),B(4,-2,-2)和C(0,5,1)等距离的点。32、设U=a-b+2c,V=-a+3b-c,试用a,b,c表示2U-3V。33、一动点与两定点(2,3,1)和(4,5,6)等距离。求这动点的轨迹方程。34、将xoz坐标面上的抛物线z2=5x绕轴旋转一周,求所生成的旋轴曲方程。35、将xoy坐标面上的圆x2+y2=9绕Z轴旋转一周,求所生成的旋转曲面的方程。36、将xoy坐标面上的双曲线4x2-9y2=36分别绕x轴及y轴旋转一周,求所生成的旋转曲面的方程。37、求球面x2+y2+z2=9与平面x+z=1的交线在xoy面上的投影方程。38、求球体x2+(y-1)2+(z-2)2≤9在xy平面上的投影方程。39、求过点(3,0,-1),且与平面3x-7x+5z-12=0平行的平面方程。40、求过点M0(2,9,-6)且与连接坐标原点及点M0的线段OM0垂直的平面方程。41、求过(1,1,1),(-2,-2,2)和(1,-1,2)三点的平面方程。42、一平面过点(1,0,-1)且平行于向量a={2,1,1}和b={1,-1,0},试求这平面方程。43、求平面2x-y+2z-8=0及x+y+z-10=0夹角弦。44、求过点(4,-1,3)且平行于直线(x-3)/2=y=(z-1)/5的直线方程。45、求过两点M(3,-2,1)和M(-1,0,2)的直线方程。46、求过点(0,2,4)且与两平面x+2z=1和y-3z=z平行的直线方程。
47、求过点(3,1,-2)且通过直线(x-4)/5=(y+3)/2+z/1的平面方程。48、求点(-1,2,0)在平面x+2y-z+1=0上的投影。49、求点P(3,-1,2)到直线x+2y-z+1=0的距离。50、求直线2x-4y+z=0,3X-y-2z=0在平面4x-y+z=1上的投影直线的方程。四、证明题1.证明不等式:2.证明不等式3.设,g(x)区间上连续,g(x)为偶函数,且满足条件证明:4.设n为正整数,证明5.设是正值连续函数,则曲线在上是凹的。6.证明:7.设是定义在全数轴上,且以T为周期的连续函数,a为任意常数,则8.若是连续函数,则9.设,在上连续,证明至少存在一个使得
10.设在上连续,证明:11.设在上可导,且,证明:华中师范大学网络教育学院《高等数学》练习测试题库参考答案一.选择题1——10ABABDCCDAA11——20ABABBCAADC21——30DCDAABCCCA31——40BABDDCCAAD41——50ABCDDCACCA51——55DDCCA二.填空题1.22.3/43.04.e-15.e-16.(31/2+1)/27.(1+)8.9/259.-1或1-10.211.-1,012.-213.1/514.0
15.0,116.C+2x3/2/517.F(x)+C18.2xe(1+x)19.020.021.21/822.271/623./3a24./625.026.2(31/2-1)27./228.2/329.4/330.21/231.032.3/233.(1,3)34.1435.36.7/637.32/338.8a39.等腰直角40.4x+4y+10z-63=041.3x-7y+5z-4=042.(1,-1,3)43.y+5=044.x+3y=045.9x-2y-2=0一.解答题1.当X=1/5时,有最大值1/52.X=-3时,函数有最小值273.R=1/24.在点(,-)处曲率半径有最小值3×31/2/25.7/66.e+1/e-27.x-3y-2z=08.(x-4)/2=(y+1)/1=(z-3)/5
9.(-5/3,2/3,2/3)10.2(21/2-1)11.32/312.4×21/2/313.9/414.(a-e)15.e/216.8a2/317.3л/1018.19.160л220.2л2a2b21.22.7л2a323.1+1/2㏑3/224.2-4/325.26.27.28.ln3/2+5/1229.8a30.5×21/231.(0,1,-2)32.5a-11b+7c33.4x+4y+10z-63=034.y2+z2=5x35.x+y2+z2=936.x轴:4x2-9(y2+z2)=36y轴:4(x2+z2)-9y2=3637.x2+y2(1-x)2=9z=038.x2+y2+(1-x)2≤9z=0
39.3x-7y+5z-4=040.2x+9y-6z-121=041.x-3y-2z=042.x+y-3z-4=043.44.==45.==46.==47.8x-9y-22z-59=048.(-5/3,2/3,2/3)49.50.四.证明题1.证明不等式:证明:令则,令得x=0f(-1)=f(1)=,f(0)=1则上式两边对x在上积分,得不出右边要证的结果,因此必须对f(x)进行分析,显然有于是故
2.证明不等式证明:显然当时,(n>2)有即,3.设,g(x)区间上连续,g(x)为偶函数,且满足条件证明:证明:4.设n为正整数,证明证明:令t=2x,有又,,所以,
又,因此,5.设是正值连续函数,则曲线在上是凹的。证明:故,曲线在上是凹的。6.证明:证明:7.设是定义在全数轴上,且以T为周期的连续函数,a为任意常数,则证明:在等式两端各加,于是得
8.若是连续函数,则证明:9.设,在上连续,证明至少存在一个使得证明:作辅助函数,由于,在上连续,所以在上连续,在(a,b)内可导,并有由洛尔定理即=0亦即,10.设在上连续,证明:证明:令故是上的减函数,又,故
11.设在上可导,且,证明:证明:由题设对可知在上满足拉氏微分中值定理,于是有又,因而,由定积分比较定理,有'
您可能关注的文档
- 上海财经大学奚君羊《国际金融学》课程习题集.doc
- 上网习题答案(宏观).doc
- 不等式选讲课后题答案.doc
- 专业技术人员《沟通与协调能力》试题与答案汇总.docx
- 专业技术人员继续教育《专业技术人员创新能力培养与提高》题库答案.doc
- 专业技术人员继续教育《沟通与协调能力》试题真题答案.doc
- 专业技术人员继续教育《职业道德》试题及答案, 完全可以考100分.doc
- 专业能力综合测试题库及答案《内燃机构造与原理》.doc
- 专升本《机械设计基础》专升本习题及答案.doc
- 世界古代文明课后习题详细答案.doc
- 世界古代文明课后题答案.docx
- 世界地理分区习题《带答案》大全.doc
- 世界科技文化史题目及答案.docx
- 东北大学《机械设计基础》习题.doc
- 东北师范大学2013年《离散数学》练习题和答案.doc
- 东北师范大学《常微分方程》1部分习题解答.pdf
- 东北财经大学《中级财务会计习题与案例》第二版 答案.doc
- 东北财经大学会计学习题与案例第二版参考答案.doc