- 1.29 MB
- 2022-04-29 13:52:55 发布
- 1、本文档共5页,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,可选择认领,认领后既往收益都归您。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细先通过免费阅读内容等途径辨别内容交易风险。如存在严重挂羊头卖狗肉之情形,可联系本站下载客服投诉处理。
- 文档侵权举报电话:19940600175。
'5-12题图5-12所示电路原已稳定,开关K在t=0时du打开,试求i(0)、u(0)和C。C1t0dt解:t<0时电路已稳定,则电容开路,电感短路,有:241i(0)i(0)6A+-LL133u(0)+Cuu(0)(0)CC24V1331-242412Vi(0)L3113
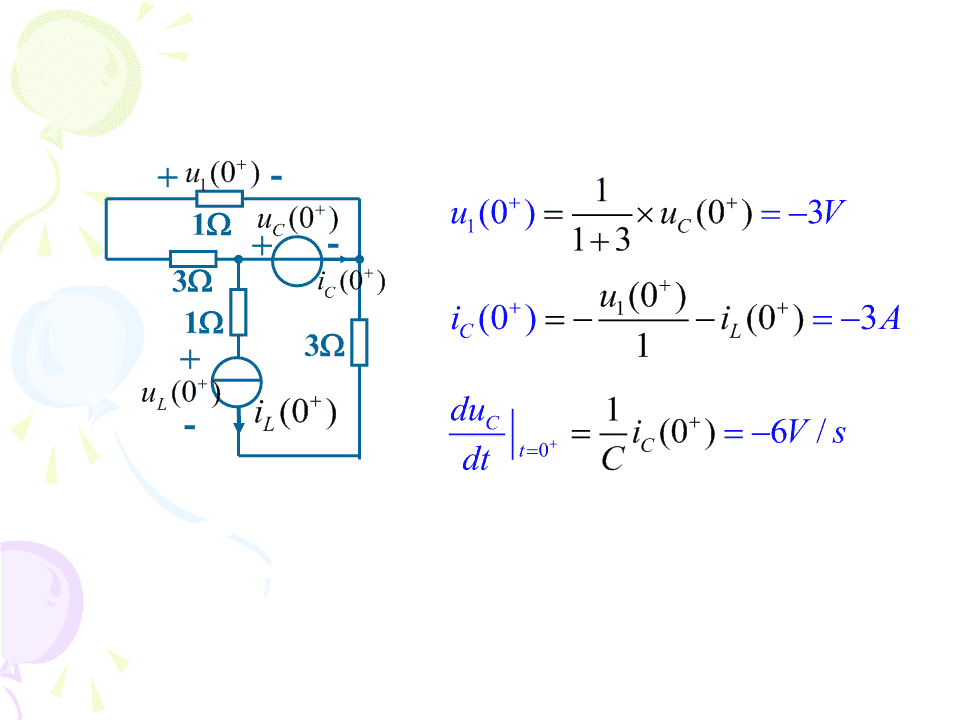
+u1(0)-1uV(0)u(0)31uC(0)1C+-133i(0)Cu(0)11iC(0)3iL(0)A+31uL(0)-iL(0)duC1i(0)6/Vst0CdtC
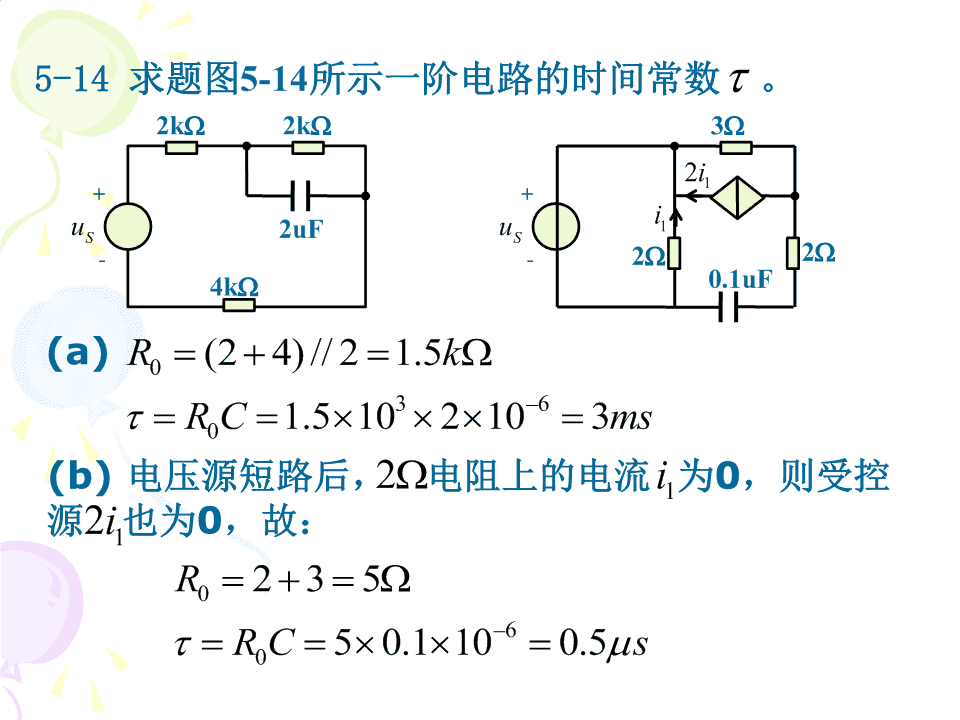
5-14求题图5-14所示一阶电路的时间常数。2k2k32i1++iuS2uFuS1--224k0.1uF(a)Rk(24)//21.5036RC1.5102103ms0(b)电压源短路后,2电阻上的电流i为0,则受控1源2i也为0,故:1R23506RC50.1100.5s0
i110i110ius0.1Hu0.2i10.2i1(c)(c1)(c)等效电阻电路如图c1,加压求流,得ui10解得:ui100/81ii0.2i故Req100/811LR/8mseq
(d)等效电阻电路如图d1332i2i1i1s2222i0.1Fi11u(d)(d1)(d)等效电阻电路如图d1,加压求流,得u43(2iii)13i1111Rui/13eq1RC1.3seq
5-25:如题所示电路已稳定,开关K在t=0时闭合,求t>0时的itL()0.5iL解:(1)求i(0)K10L-iA(0)10图如图a所示,则L51HiL由换路定则iLL(0)i(0)1A1A45V10(2)求iL(),∞图如图b所示,则有5[()1]10[()10.5()]10iLiLiLiL()450.5()iL10iA()3Li(0)L5i()L1A1A45V1010(a)0-图(b)∞图
0.5iL(3)求10iL等效电阻电路如图d所示,加压求流u10i5i10(i0.5)20iiLLLLL5uRui/20eqL10LR/1/20seq(b)等效电阻电路(4)求itL(),由三要素公式,得t20tit()i()i(0)i()e32eAt,0LLLL
5-36题图5-36(a)电路中,已知iAL(0)1,其utS()波形如图(b)所示,试求itL()。utV()/S1it()L+2utS()1H-1ts/2451)求零输入响应:由换路定则可知:iLL(0)i(0)1,At1siLzi()teAt,02)求零状态响应:t当utS()()t时,SAiL()1;StiL()(1e)()t当utS()(t2)(t4)2(t5)时,(t2)(t4)(5)ti()[1te](t2)[1e](t4)2[1e](t5)Lzs
3)求全响应:it()i()ti()tLLziLzst(t2)(t4)(t5)e[1e](t2)[1e](t4)2[1e](t5)A,0t
7-4已知三个同频率的正弦电流:i110sin(t120)A,i220cos(t150)A,i330cos(t30)A。试比较它们的相位差。解:i110sin(t120)10cos(t30)Ai20cos(t150)A2i30cos(t30)30cos(t150)A330(150)180121501503006023231503012031
7-5试求下列正弦量的振幅向量和有效值向量:(1)i5costA(2)i10cos(t)A122(3)i15sin(t135)A3解:(1)i15costAI1m50AI,12.5203.540A(2)i10cos(t)10cos(t)222I10AI,52A22m22(3)i15sin(t135)15cos(t225)15cos(t135)3I15135AI,7.52135A10.605135A33m
7-13试求题图7-13所示电路的输入阻抗和导纳,以及该电路的最简串联等效电路和并联等效电路10rads/。(1jj1)(1)3j3解:Zj33aab(1jj1)(1)1j111j33jj112jb13j3.20.24H3jj33.22.4a511bY0.2j0.15SabaZ1612abj0.2S550.67Hb
7-15试求题图7-15所示各二端网络的输入阻抗。j12HI"aa解:j2UU"4HuU2u2bb0.5rads/U""jIjUUUI"(2//2)jj4U"jI"(1jI)"(2jI1)"22jZj(21)i
7-16在题图7-16所示电路中,已知U15,VU12,VCLUV4,求电压U为多少?R+U-+U-ICL+U-22R解:UUR()ULUC+U-224(1215)5VULIURUUC
7-18RL串联电路,在题图7-18(a)直流情况下,电流3表的读数为50mA,电压表的读数为6V。在f10Hz交流情况下,电压表V读数为6V,V读数为10V,如12图(b)所示。试求R、L的值。ii1A解:直流时电感相当于RU1V1R短路,则:UVUV22LULU6LUR1203II5010()a()bULU交流时相量图如图(c),则:2I221UUU8VU1L21()cUU1LUR8120LL25.5mHRLU210361
7-19题图7-19所示电路,已知电流表A1的读数为10A,电压表V1的读数为100V;试画相量图求电流表A2和电I压表V2的读数。CIA2I1CjXCU1Ij102A2V1-++UC2-IU1I1-1+U25j5UVC2U22解:设各电压、电流如图,且设U为参考向量,则:1UU110U1000IA10901CjXX90CCU11000IA10245155j5245故由相量图可得:I21IIC100A由相量图:UC22(j10)I10090VU2UC2U1100245
7-23(b)试求题图7-23所示有源二端网络的戴维南等效电路。I1I1I+j1+2I-+j1+2I-+11502j2UOC2j2U---解:(1)求开路电压UOC:U2I(jI)11U2I(jI1)50OC111I5050或:j11II(分流公式)jj1(2//2)1111UjOC5552135jj122(2)求等效阻抗Z:0可得:U(3jI1)U2I(jI)11Zj(31)0(j1)(I)(j1)(I)11II122j
I1+j1+2I-150-2j2+戴维南等效电路图:52135-31j说明:若给的图是时域的,则等效戴维南电路图也必须是时域的,即:要将Zj0(31)转换成一电阻串联电感。
7-25(2)已知关联参考方向下的无源二端网络的端口电压u(t)和电流i(t)分别为u(t)10cos(100t70)V和it()2cos(100t40)A,试求各种情况下的P、Q和S。解:先将各量写成相量形式:U5270,VI240APUIcos522cos3053WzQUIsin522sin305VarzSUI10VA*另解:SUI5270240103053j5P53,WQ5VarS,10VA
7-27二端网络如题图7-27所示,已知UV500,电源S提供的平均功率为312.5W,试求XC的数值。+j8ISIRII+Lj8CUS88UjXjX-CC-解:将电路等效为诺顿模型,并设各支路电流和电压如相量模型图所示,其中:USIA6.2590Sj82PIR312.5I6.25ARR22ISIRICIL即=ISI-ICLIR且IRISUUII而I,IX8CLCLCX8C
7-29正弦稳态电路如题图7-29所示,若Z可变,试问L为何值时可获得最大功率?最大功率P为多少?maxaa2a2+2402j4ZL402j4U2j4Z0OCb-bb解:1)求开路电压U:OC2890U40j44245VOC22j42452)求等效阻抗Z0:490Z(22)//4j2j20245*3)当ZLZ022j时,最大功率为:22U(42)PWOCm4max4R420
7-30电路如题图7-30所示,试求负载Z为何值时可获L得最大功率?最大功率P为多少?maxI0+j10.5+j10.5+20V1Z20V1UOC2IL2I--I1-I10110解:U2I(0.5j1)20IOC10j10.5+20UIA2012I101-1I1U22j22445VOCI0A2I0Zj0.511102*Uoc当ZLZ00.5j1时,可获得最大功率:PWmax=84R0
7-31已知三相电路中星形连接的三相负载每相阻抗Zj1216,接至对称三相电源,其线电压为380V。若端线阻抗忽略不计,试求线电流及负载吸收的功率;若将此三相负载改为三角形连接,线电流及负载吸收的功率将变成多少?AAUV3800解:+++ABUAZUAU1--ABUU30AAB-3CBCZZB22030VU2203022030AIA1183.1AZj12162053.1II11AlPP3UIcos322011cos53.14356WPPZ
A++UAU-ABUV3800Z-ABCBU38003800ABIA1953.1ABZj12162053.11I19AII32.9APll3P3UIcos338019cos53.112996WPPZ
7-41题图7-41所示二端网络N的端口电流、电压分别为it()5cost2cos(2t),A4ut()3cos(t)cos(2t)cos(3t)V243试求网络吸收的平均功率。3解:PUIkkcosZkk0UIUIcosUIcos()00112222152130cos2cos()022222
7-42已知流过2电阻的电流it()222cost2cos(2t30),A试求电阻消耗的平均功率。2解:2PIRkk0222222(IIIR)(221)218W012
8-2(c)写出题图8-2各耦合电感的伏安关系。didii1Mi212uLM11dtdt+-uL1L2udidi12uL21M22-+dtdt题图8-2解:因为u1与i1不关联,故L1的自感电压取负;又因为u1的正极性端与电流i2的流入湍为同名端,故L的互感电压取正;1因为u与i关联,故L的自感电压取正;222又因为u2的正极性端与电流i1的流入湍为异名端,故L的互感电压取负;即:2
8-3试求题图8-3中的电压u。22H53Hi1i2+i1i2+++2t3H10costV5H4Hu3(1eA)4Hu22----题图8-3(a)题图8-3(b)解:(a)i0,故:2di2t1de[3(1)]2tuM2212eVdtdt520(b)i20,故:IA114555jUjMI345V21u32cos(t45)V2
8-4耦合电感L6,HL4,HM2H,试求题图8-412中三种连接时的等效电感Leq。MMi2LM1LM2LeqL1L2LeqL1L2LeqM(a)i0i0题图8-4(1)(2)解:(a)两线圈电流i为0,因此两电感可等效为如解图8-4(a)-(1)所示的三端连接,经去耦等效为解图8-4(a)-(2);LLMML6Heq11
(b)同(a),L1和L2为同名端相连的三端连接,去耦等效如解图8-4(b),则等效电感为:L(LM)(LM)//Meq12ML()M2=LM5H1LMM2LM1LM2LM1MLeqLeqLMM2解图8-4(b)解图8-4(c)(c)L和L为异名端相连的三端连接,去耦等效如解12图8-4(c),则等效电感为:L(LM)(LM)//(M)eq12ML()M2=LM5H1LMM2
38-6电路如题图8-6所示,10radsL/,12L1,HM0.5,HCC1F,试求Zab和Zad。12C1aMcLL12bCd2题图8-6解:(1)求Z:ab从a、b两端看入,因为c、d端上电流为0,故原电路可等效为如解图8-6(1)-(a)所示,而L和L为同12名端相连的三端连接,经去耦等效后如解图8-6(1)-(b),则:
aaMMLML22LLM1C1C11C2C2bb(a)解图8-6(1)(b)11ZjMj(LM)//j(LM)ab12jCjC12=j500+j500//[j500-j1000-j1000]=j1250
(2)求Z:ad从a、d两端看入,因为b、c端上电流为0,故原电路可等效为如解图8-6(2)-(a)所示,而L和L为同名12端相连的三端连接,经去耦等效后如解图8-6(2)-(b);aaMMLLLM1LM212RCCC2121dd(a)解图8-6(2)(b)11ZjMj(LM)//j(LM)ad12jCjC21=j500+[j500-j1000]//[j500-j1000]=j250
8-11题图8-11所示电路中,试求当ZL为多大时可获得最大功率,以及它获得的最大功率为多少?10ka10kjk2.jk8jk8++2000V2000VZjk10jk10ZLL--jk2.b题图8-11解图8-11解:去耦等效后的电路如图:(1)求Z以左的等效阻抗Z:L0Z(10j8)//2jj8(0.2j9.8)k0故,ZZ(0.2j9.8)k时,可获得最大功率。L0
10kI0jk8jk8+2000VZL-jk2解图8-11(2)求ZL以左的开路电压Uoc:j2UV200020245OC10jj82故,Z可获得的最大功率为:L22U(202)OCPW1Lmax34R40.2100
8-12在题图8-12所示电路中,已知US200V,试求电流相量I。3I122:1I+US+31US1212--题图8-12(a)题图8-12解:将变压器初级的元件折合到次级如图8-12(a),可得U/231003IS33//113343+420A
8-13试求题图8-13所示的正弦稳态电路中的it()和ut()。-ut()+IUC-+j8it()0.025FIII121:31:3IR+18+++102cos5tV100VUU1812----题图8-13解:电路的相量模型如解图8-13;解图8-13I3I5j7.5AUUU2U20012211III5j55245AU55U21CI90AI,0ACRj82183u(t)202cos5tV55IIIjA2RCi(t)10cos(5t45)A32
8-14试求题图8-14所示电路中的电流向量I。XI100.5:10.5I11+。。++0.5U2.U2-j50500V---I0.5I1110IX解:理想变压器的问题,一种方法是利用阻抗搬移,另一种方法是可直接利用初、次级线圈间电压、电流的线性关系。(1010)I100.5I5000.5U11210I(10j50)0.5IU112IA22451II0.5I245Ax11
8-17电路如题图8-17所示,为使负载RL获得最大功率,试问理想变压器的匝比n应为多少?最大功率Pmax为多60n:1少?60n:1-j8I-j8++j302200Vj30RLnRL-2-55n解图8-17题图8-17解:将次级线圈的阻抗搬移到初级线圈中,如解图8-17;ab以左部分电路的等效电阻为:Zj860//3012jj160222故,当5n1216,即n=2时,电阻上可获得最大功率。200j301IA36.960j30//(20j8)j3020j8422PmaxInRL()1.25W
8-20题图8-20所示的电路原已稳定,t=0时开关K闭合,求t>0时电流it1()和电压ut2()。Kit()K42:1it()40.6H11t0t0+1.5++++6V1.2H0.3Hut2()1.56V1.2Hut1()ut2()6V-----题图8-20(a)解图8-20(1)解:由于MLL0.6H,故为全耦合变压器,电路等效为如解12图8-20(1)-(a);其中:Ln2:1L2次级线圈的阻抗搬移到初级线圈后的电路模型如解图8-20(1)-(b);
9-1试求题图9-1所示电路的转移电压比,并定性绘出其幅频特性曲线和相频特性曲线。++LURU12--(a)UR12解:a)Kj()UURjL11jRR1L令L,则:Kj()LU1j1LKj()U()jarctg2L1L
当0时:KjU()1(j)01当C时:KjU()0.707()j24当时:KjU()0()j2曲线类似书图9-2。
9-6题图9-6是应用串联谐振原理测量线圈电阻r和电感L的电路。已知R10,C0.1F,保持外加电压U有效值为1V不变,而改变频率f,同时用电压表测量电阻R的电压U,当f800Hz时,UV0.8,试求电阻rRRmaxR和电感L。R+++UR-rU+U-r+R-Lr+UULULC--C+-UC-解:等效电路如图所示;由于f800Hz时,电路发生串联谐振,即:UULC000故有:URmaxUr0UUr010.80.2VUUURmaxr0r0r2.5RrURmaxR
1LC11LH0.422C(2f)C
9-8已知题图9-8并联谐振电路的谐振频率f01MHz,通频带BW2kHz,谐振阻抗Zk8,求参数r、L0和C的值。++rUCUCLR0SSL--解:这是一个实际的并联谐振电路,其等效电路如图所示;且3LC995pFRZ81000CrL=25.5H116Lf1000r=3.2C2LC0ff100BWQ2fRCC00QBW2RBW0
9-9题图9-9电路发生并联谐振,已知理想电流表A读1数10A,电流表A读数8A,求理想电流表A2的读数。II1IIR"IA1A1I1"++CII2U2USA2SA2LL--AA""解:将RC串联支路等效为RC,则等效电路如图所示;IRC""II1而因为谐振,故有:II"R2222I""IIII6ACR11I2I"6AC
9-10题图9-10所示并联谐振电路,L0.1mHC,100pF,r10,RSS100k,U20,试求(1)谐振角频率0;(2)"端电压U;(3)整个电路的品质因数Q;(4)谐振时电容支路电流IC0及电感支路电流ILr0。ILr0+ILr0+IIIRrC0L0R0SUS+UCRSUCLR0RULSS---解:这是一个实际的并联谐振电路,其等效电路如图L所示;且:Rk10001Cr7(1)10rads/0LCUS(2)U(R//R)10VS0RSC"0(3)QCRCR(//R)5000S0G
ILr0+IIIC0L0R0USRSUCLR0RS-"US(4)IC0jQ190mA()或IC00jCURSII190mAL0C0URSSI0.010mAR0RRRSS0III0.0101900.01jmA1Lr0LR00
9-14题图9-14所示电路中,已知utS()10cos314t2cos3314,()2cos3314,tVut0tVC9.4F试求L和L的值。CL112ab+L+2ut()Rut()S0--解:1314时,utS()的该频率分量在R上的电压为零,故,相当于ab端在该频率时开路,即LC回路发生并联谐振,则:1314LH0.9612()LLC1223314时,utS()的该频率分量全部作用在R上,故,此时LC回路发生串联谐振,即相当于ab端在该频率时短路,则:13314LH0.1221LC1
11-1(a)求题图得11-1所示二端网络的Z参数。I1I211I1122"2++2+2U122U21U12"--"-12"11解:利用Z参数的定义求解。设端口电压、电流如图,则有:U1Z(12)//(21)1.511I1I02I10时等效电路如右图,则有:II2221U122Z0.512II22I01因原网络是线性无源二端网络,有:ZZ21120.5
211"112I"222-U+2U2Z(12)//(21)1.522I2I011.50.5Z0.51.5
11-1(b)求题图11-1所示二端口网络的Z参数。βIβIRRIIRbCIIIbI121。12。1。。22RRccUUUU1R21Re2e1′。。2′1′。。2′U12RIbeRI()IU()RRIRI12beeURI(I)RI(I)U(RRI)(RRI)2ce2222ececRRRbeeZRRRRecec
11-2(a)求题图得11-2所示二端口网络的Y参数。1-U2+1I11I112++22(1)"11I22U1U12I"--"1112解:设端口电压、电流如图,则有:"U0,相当于2和2端短路,故:2I151YS11U1//(11//1)31U02"U0,相当于1和1端短路,等效电路如右图,1则:U21U1I211//1241YS12UU322U01
而该网络是线性无源二端对称网络,则有:54YYSY,YS22112112335433YS4533
11-2(b)求题图11-2所示二端口网络的Y参数。1I1CI22.方法二:利用参数方程求解。+.UURgmUUU12I1jCU()1U2_R1"2"IgUjCU()U题图11-2(b)2m1121I(jCU)(jCU)112RI()gjCUjCU2m121jCjCYSRgjCjCm
12-2题图12-2所示电路中,若非线性电阻的伏安关2系为iu0.13u,试求电流i。1Ω2Ω1Ω1Ωi0+i++++i2Vu2V2Ωu2V2ΩuOC_____1ΩZ241222Ω0uV2ZOC012312342+2uiu0.77,Vi0.845A4i33113Vu3_2u2220,Vi32Aiu0.13u'
您可能关注的文档
- 工》判断题_706T_(带答案).doc
- 与波简明教程》课后答案_杨儒贵_刘运林_科技出版社.doc
- 《电磁场与电磁波》(陈抗生)习题解答选.doc
- 第4版(谢处方_编)课后习题答案_高等教育出版社.pdf
- 《电磁场与电磁波》试题含答案.pdf
- 《电网调度自动化厂站端调试检修员》技能鉴定题库 2016(无答案版).doc
- 《电路与模拟电子技术》第二版(殷瑞祥主编) 课后习题答案 高等教育出版社.doc
- 《电路与模拟电子技术》课后习题答案.doc
- 《电路分析》习题讲解.pdf
- 《电路分析基础》试题及答案.doc
- 《电路原理》 张燕君版 第1-9章习题答案.pdf
- 《电路理论(上)》试题集及参考答案.doc
- 《画法几何及工程制图B》复习题及参考答案.doc
- 《画法几何及机械制图习题集》参考答案.pdf
- 《病理生理学》习题集-人卫第8版(精心整理).doc
- 《病理生理学》练习册参考答案.doc
- 《相似三角形》经典练习题(附答案).doc
- 《矢量分析与场论》习题解答.doc