- 1.38 MB
- 2022-04-29 14:04:15 发布
- 1、本文档共5页,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,可选择认领,认领后既往收益都归您。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细先通过免费阅读内容等途径辨别内容交易风险。如存在严重挂羊头卖狗肉之情形,可联系本站下载客服投诉处理。
- 文档侵权举报电话:19940600175。
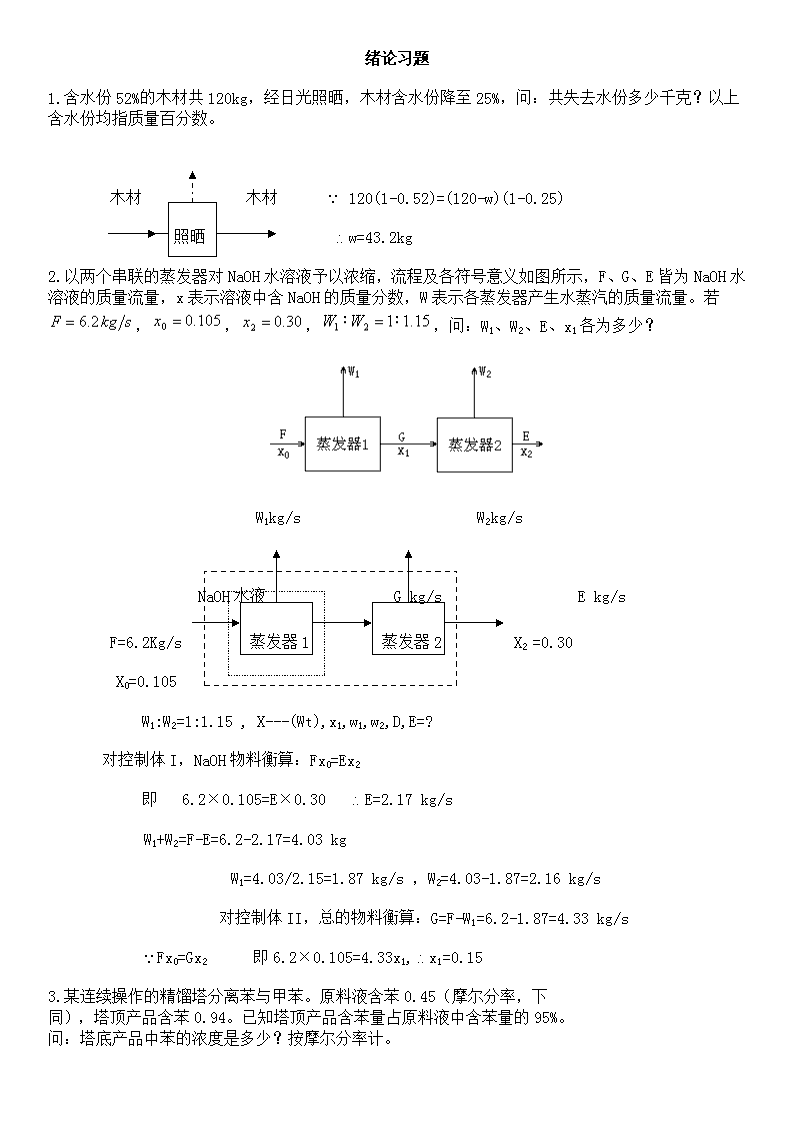
'绪论习题1.含水份52%的木材共120kg,经日光照晒,木材含水份降至25%,问:共失去水份多少千克?以上含水份均指质量百分数。木材木材120(1-0.52)=(120-w)(1-0.25)照晒w=43.2kg2.以两个串联的蒸发器对NaOH水溶液予以浓缩,流程及各符号意义如图所示,F、G、E皆为NaOH水溶液的质量流量,x表示溶液中含NaOH的质量分数,W表示各蒸发器产生水蒸汽的质量流量。若,,,,问:W1、W2、E、x1各为多少?W1kg/sW2kg/sNaOH水液Gkg/sEkg/sF=6.2Kg/s蒸发器1蒸发器2X2=0.30X0=0.105W1:W2=1:1.15,X---(Wt),x1,w1,w2,D,E=?对控制体I,NaOH物料衡算:Fx0=Ex2即6.2×0.105=E×0.30E=2.17kg/sW1+W2=F-E=6.2-2.17=4.03kgW1=4.03/2.15=1.87kg/s,W2=4.03-1.87=2.16kg/s对控制体II,总的物料衡算:G=F-W1=6.2-1.87=4.33kg/sFx0=Gx2即6.2×0.105=4.33x1,x1=0.153.某连续操作的精馏塔分离苯与甲苯。原料液含苯0.45(摩尔分率,下同),塔顶产品含苯0.94。已知塔顶产品含苯量占原料液中含苯量的95%。问:塔底产品中苯的浓度是多少?按摩尔分率计。
[解]:0.95==4.导热系数的SI单位是W/(m·℃),工程制单位是kcal/(m·h·℃)。试问1kcal/(m·h·℃)相当于多少W/(m·℃)?并写出其因次式。1kcal/(m.h.0C)=?J/(m.s.0C)写出导热系数的因次式。∵1kcal=4.187×103J,1h=3600s∴5.已知理想气体通用常数物理大气压·升/(摩尔·K),试求采用J/(kmol·K)时R的数值。解:写出以J/(kmolk)的单位为理想气体通用常数R之值。∵1物理大气压=1.0133×105N/m2,1升=10-3m3∴R=0.082056.水蒸汽在空气中的扩散系数可用如下经验公式计算:
式中 D——扩散系数,英尺2/h;p——压强,atm;T——绝对压强,。试将上式改换成采用SI单位的形式。各物理量采用的单位是:D—m2/s,p—Pa,T—K。解:经验公式的单位换算:物理量扩散系数压强绝对温度原来单位英尺2/hatm0R后来单位M2/sPaK∵1英尺2/h=0.30482/3600m2/s=2.58×10-5m2/s,1atm=1.0133×105pa,温差1k=1.80R7.在冷凝器中蒸汽与冷却水间换热,当管子是洁净的,计算总传热系数的经验式为:式中 K——总传热系数,Btu/(ft2·h·℉);u——水流速,ft/s。试将上式改换成采用SI单位的形式。各物理量采用的单位是:K—W/(m·℃),u—m/s。解:经验公式的单位换算:物理量传热系数流速原来单位BUT/ft2.h.0F)ft/s后来单位W/(m2.K)m/s∵1BUT/(ft2.h.0F)=5.678W/(m2.K),1ft/s=0.3048m/s
《第一章流体流动》习题解答1.某敞口容器内盛有水与油。如图。已知水及油的密度分别为1000和860kg/m3,解:h1=600mm,h2=800mm,问H为多少mm?2.有一幢102层的高楼,每层高度为4m。若在高楼范围内气温维持20℃不变。设大气静止,气体压强为变量。地平面处大气压强为760mmHg。试计算楼顶的大气压强,以mmHg为单位。3.某水池,水深4米,水面通大气,水池侧壁是铅垂向的。问:水池侧壁平面每3米宽度承受水的压力是多少N?外界大气压为1atm。4.4.外界大气压为1atm,试按理想气体定律计算0.20at(表压)、20℃干空气的密度。空气分子量按29计。5.5.有个外径为R2、内径为R1为的空心球,由密度为ρ’的材料制成。若将该球完全淹没在某密度为ρ的液体中,若球能在任意位置停留,试求该球的外径与内径之比。设球内空气重量可略。6.6.为放大以U形压差计测气体压强的读数,采用倾斜式U形压差计。如图。指示液是ρ=920kg/m3的乙醇水溶液。气体密度为1.20kg/m3。读数R=100mm。问p1与p2的差值是多少mmHg?7.采用微差U形压差计测压差。如图。已知U形管内直径d为6mm,两扩大室半径均为80mm,压差计中用水和矿物油作指示液,密度分别为1000及860kg/m3。当管路内气体压强p与外界大气压p0相等时,两扩大室油面齐平,U形管两只管内油、水交界面亦齐平。现读得读数R=350mm,试计算:(1)气体压强p(表)。(2)若不计扩大室油面高度差,算得的气体压强p是多少?(3)若压差计内只有水而不倒入矿物油,如一般U形压差计,在该气体压强p值下读数R0为多少?
8.某倾斜的等径直管道内有某密度ρ的液体流过。如图。在管道的A、B截面设置了两套U形压差计测压差,下测用的是一般U形压差计,上测用的是复式U形压差计,所用的指示液均为密度是ρ1的同一种液体。复式压差计中两段指示液之间的流体是密度为ρ的流过管道内的液体。试求读数R1与R2、R3的关系。9.将水银倒入到图示的均匀管径的U形管内,水银高度h1=0.25m。然后将水从左支管倒入,测得平衡后左支管的水面比右支管的水银面高出0.40m。试计算U形管内水与水银的体积比。 解:R1=0.4mR2h1=0.25m11 L=0.015mL习题9附图如图所示1--1为等压面,p1=p1’r水g(R1+R2)=r水银gR2103´(0.4+R2)=13.6´103R2R2=0.0317mV水银=d2(2h1+L)V水=d2(R1+R2)V水银/V水=(2h1+L)/(R1+R2)=(2´0.25+0.015)/(0.4+0.0317)=1.1910.一直立煤气管,在底部U形压差计h1=120mm,在H=25m高处的U形压差计h2=124.8mm。U形管指示液为水。管外空气密度为1.28kg/m3。设管内煤气及管外空气皆静止,求管内煤气的密度。 h2H h1 习题10附图p2p2’解:
Hp1p1’ p1-p1’=r水×gh1¼¼(1)p2-p2’=r水×gh2¼¼(2)(1)减(2),得(p1-p2)-(p1’-p2’)=r水×g(h1-h2)¼¼(3)其中p1-p2=r煤×gH,p1’-p2’=r空×gH,代入(3)式,得:r煤×gH-r空×gH=r水×g(h1-h2)即r煤=r水×(h1-h2)/H+r空=103(0.120-0.1248)/25+1.28=1.088kg/m311.以2”的普通壁厚的水煤气钢管输送15℃的清水,水在管内满流。已知水流速u=1.5m/s,求水的质量流量、质量流速和体积流量。12.如图所示,质量为3.5kg,面积为40×46cm2的一块木板沿着涂有油的斜面等速向下滑动。已知v=1.2m/s,σ=1.5mm(油膜厚度)。求滑油的粘度。135 12vd 13解:ta512VaGd 从受力分析Gsina=tAmgsina=tAt==3.5´9.81´/(40´46´10-4)=71.77N/m2t=m=m
m==71.77´1.5´10-3/1.2=0.0897Pa×s13.以压缩空气将某液体自储槽压送到高度H=5.0m、压强p2为2.5at(表压)的容器内,如图。已知液体密度ρ=1800kg/m3,流体的流动阻力为4.0J/kg。问:所需的压缩空气压强p1至少为多少at(表压)?14.水以70m3/h的流量流过倾斜的异径管通。如图。已知小管内径dA=100mm,大管内径dB=150mm,B、A截面中心点高度差h=0.3m,U形压差计的指示液为汞。若不计AB段的流体流动阻力,试问:U形压差计哪一支管内的指使液液面较高?R为多少?15.水以6.4×10-4m3/s的流量流经由小至大的管段内。如图。小管内径d1=20mm,大管内径d2=46mm。欲测1、2两截面处水的压差,为取得较大的读数R,采用倒U形压差计。已知压差计内水面上空是ρ=2.5kg/m3的空气,读数R=100mm。求水由1至2截面的流动阻力∑hf。16.水从喷嘴口1-1截面垂直向上喷射至大气。如图。设在大气中流束截面保持圆形,已知喷嘴内直径d1=20mm,出喷嘴口水流速u1=15m/s。问:在高于喷嘴出口5m处水流的直径是多大?忽略摩擦阻力。
解:1--1与2--2之间列柏努利方程22gz1+u12/2+p1/r=gz2+u22/2+p2/rz1=0,z2=5m,p1=p2u12/2=gz2+u22/2152/2=9.81×5+u22/211u2=11.26m/s又,u1d12=u2d22习题16附图d2=(u1/u2)1/2d1=´0.020=0.0231m17.高、低水库的水面高度差H=42m,水流量为30m3/s,水流的总阻力为4.5mH2O。如图。已知透平的效率η=0.78,试计算透平的输出功率。解:u1=u2=0,p1=p2,z2=0,11z1=H=42m1--1与2--2间列柏努利方程Hgz1+u12/2+p1/r+Ws=gz2+u22/2+p2/r+ShfWs=-gz1+Shf=-9.81´42+4.5´9.81´103/10322=-368J/kgNa=Ws×Vr=-368´30´103=1.10´107WNe=Na×h=1.10´107´0.78=8.61´106W=8.61´103kW18.某水溶液在圆直、等径管内层流动。管内半径为R。设测点流速的探针头位置与管轴线的距离为r。问:测点相对位置为多少时该点的点流速等于平均流速?19.以水平圆直管输送某油品。管内径为d1,管两段压差为。因管道腐蚀,拟更换管道。对新装管道要求如下:管长不变,管段压降为原来压降的0.75,而流量加倍。设前后情况流体皆为层流。问:新管道内径d2与原来管内径d1之比为多少?20.在机械工程中常会遇到流体在两平行固体壁的间隙中作一维定态流动的情况。如图。设流动为层流。设间隙厚为2y0,试证流体沿y轴向点流速呈如下抛物线规律分布:
解:对长度L,高度y,宽度为1的流体元作受力与运动分析:21.粘度为μ,密度为ρ的液体沿铅垂向平壁膜状流下。如图。设液体层流流动,液膜厚度为δ,平壁宽度为B。试推导任一流动截面上液体点流速v随y的变化规律,并证明平均流速解:取宽为B,长为dx,高为y的流体元作受力与运动分析:22.串联两管1、2,d1=d2/2,L1=80m,Re1=1600,Shf1=0.54m液柱,Shf2=56mm液柱,求L2。局部阻力可略。解:∵Re=µ,Re,2/Re,1=d1/d2=1/2,Re,2=Re,1/2=1600/2=800,两管内皆为层流又,Shf=32mul/(rgd2)µ32mVl/(d2rgd2)µl/d4Shf,2/Shf,1=(d1/d2)4´l2/l1即56/540=(1/2)4´l2/80l2=133m23.原r1=920kg/m3,m1=1.30P,现r2=860kg/m3,m2=1.15P,层流,W2/W1=1.30求:Dpf1/Dpf2。局部阻力不计。解:层流,Dpf=32mul/d2=32mWl/(d2´r´d2)µDpf,2/Dpf,1=(m2/m1)´(W2/W1)´(r1/r2)=´1.30´=1.23 24.某牛顿型流体在圆、直、等径管内流动,在管截面上的速度分布可表达为v=24y-200y2,式中:y¾截面上任一点至管壁的径向距离,m;v¾该点的点流速,m/s。试求:(1)管半径中点处的流速。(2)管壁处的剪应力。该流体的粘度为0.045Pa×s。解:若为层流,v=vmax[1-(r/R)2]=vmax[(R2-r2)/R2]=vmax(R-r)(R+r)/R2
=vmaxy(2R-y)/R2=2vmaxy/R-vmaxy2/R2可见,该流型为层流∵2vmax/R=24,vmax/R2=200,二式相除,得(vmax/R2)/(2vmax/R)=1/(2R)=200/24R=0.06mi.y=0.06/2=0.03m,v=24y-200y2=(24´0.03)-(200´0.032)=0.54m/sii.dv/dy=24-400y,dv/dy½y=0=24tw=m(dv/dy)y=0=0.045´24=1.08N/m225.W=35T/h,H=20m,j108´4mm,m=2840cP,r=952kg/m3,h=50%,N=85kW,求包括局部阻力当量管长的总管长。解:W=35T/h=35´103kg/hd=108-4´2=100mm=0.1m,m=2840cP=2.84Pa×sNe=Nh=85´103´0.5=4.25´104WWs=Ne/W=4.25´104´3600/(35´103)=4371J/kg1--1与2--2间列柏努利方程gz1+u12/2+p1/r+Ws=gz2+u22/2+p2/r+Shfz1=0,z2=H=20m,u1=u2=0,p1=p2Ws=gH+ShfShf=Ws-gH=4371-9.81´20=4175J/kgu===35´103/(3600´952´´0.12)=1.30m/sRe===43.6<2000层流l===1.47∵Shf=l××u2/2=×2/u2=´2/1.302=336m26.某有毒气体需通过一管路系统。现拟用水在按1/2尺寸缩小的几何相似的模型管路系统中做实验予估实际气流阻力。实际气体流速为20.5m/s,密度为1.30kg/m3,运动粘度为0.16cm2/s。实验用水的密度为1000kg/m3,运动粘度为0.01cm2/s。为使二者动力相似,水流速应为多少?若模型实验测得流动阻力为15.2J/kg,实际气体的流动阻力是多少?欲满足动力相似,必须Re,其=Re,水,设气体管径为d,即
27.某实验室拟建立流体通过圆直、等径管内的阻力测试装置,有两个方案,一个方案是采用20℃清水为工质,水流速不超过3.0m/s;另一方案以p=1atm、20℃空气(按干空气计)为工质,流速不超过25.0m/s,要求最大。问:两方案需要的管内径各为多少?若管子绝对粗糙度皆为0.1mm,二者管长与管内径之比都是150,采用以上算得的管径(需按无缝钢管选接近的规格),问:二者最大流速时管路阻力各为多少?28.试证明流体在圆管内层流时,动能校正系数。29.试按规律推导湍流的值。
30.某牛顿型流体在圆、直、等径管内流动,管子内半径为50mm。在管截面上的流速分布可表达为,式中:y——截面上任一点至管壁的径向距离,m;v——该点的点流速,m/s。试求:(1)流型;(2)最大点流速vmax。解:设v=vmax(1-r/R)1/6=vmax()1/6=(vmax/R1/6)×y1/6,故该流型为湍流。又∵vmax/R1/6=vmax/(0.050)1/6=2.54vmax=1.54m/s31.某直管路长20m,管子是1”普通壁厚的水煤气钢管,用以输送38℃的清水。新管时管内壁绝对粗糙度为0.1mm,使用数年后,旧管的绝对粗糙度增至0.3mm,若水流速维持1.20m/s不变,试求该管路旧管时流动阻力为新管时流动阻力的倍数。32.某流体在光滑圆直管内湍流流动,设摩擦系数可按布拉修斯公式计算。现欲使流量加倍,管长不变,管内径比原来增大20%,问:因摩擦阻力产生的压降为原来的多少倍。33.如图所示,某液体在光滑管中以u=1.2m/s流速流动,其密度为920kg/m3,粘度为0.82cP。管内径为50mm,测压差管段长L=3m。U形压差计以汞为指示液。试计算R值。 11
L22 R习题33附图解:在1--1与2--2间列柏努利方程:gz1+u12/2+p1/r=gz2+u22/2+p2/r+Shf或(pm,1-pm,2)/r=Shf(u1=u2)(ri-r)gR/r=(0.3164/Re0.25)´´u2/2其中Re==0.05´1.2´920/(0.82´10-3)=6.73´104则(13.6-0.92)´103´9.81R/920=[0.3164/(6.73´104)0.25]´(3/0.050)´(1.22/2)R=6.28´10-3m34.有一高位水槽,其水面离地面的高度为H。如图。水槽下面接有2”普通壁厚水煤气钢管130m长,管路中有1只全开的闸阀,4只全开的截止阀,14只标准90°弯头。要求水流量为10.5m3/h,设水温20℃,ε=0.2mm,问:H至少需多少米?35.承第34题,若已知H=20m,问水流量多少m3/h?
36.有两段管路,管子均为内径20mm、长8m、绝对粗糙度0.2mm的直钢管,其中一根管水平安装,另一根管铅垂向安装。若二者均输送20℃清水,流速皆为1.15 m/s。竖直管内水由下而上流过。试比较两种情况管两端的额修正压强差与压强差。要用计算结果说明。37.有A、B两根管道并联。已知:lA=8m,dA=50mm,lB=12m,dB=38mm(上述l中包含了局部阻力,d指内径)。流体工质是常压、20℃的空气(按干空气计)。总流量是200kg/h。问:B管的质量流量是多少?分支点与汇合点的局部阻力可略。ε皆为0.2mm。
38.某水塔供水流程如附图的a)图所示,管长为L。现需增加50%的流量,拟采用b)流程。b)流程中各管管径均与a)流程的相同,其L/2管长为两管并联。设局部阻力不计,所有管内流体流动的摩擦系数λ值均相等且为常数。问:b)方案能否满足要求。39.某七层的宿舍楼,第四至第七层楼生活用水均来自房顶水箱。如图。若总输水管为普通壁厚水煤气钢管,各层楼自来水支管为普通壁厚水煤气钢管。所用的阀皆为截止阀。水箱内水深2m。有关尺寸示于附图。试计算:(1)只开七楼的阀且阀全开时,V7为多少?(2)当四楼及七楼的阀都全开,五、六楼的阀全关,V4及V7及各为多少?计算支管阻力时只计入局部阻力,直管阻力可略。设λ皆为0.040。
40.用离心泵将水由水槽送至水洗塔内。水槽敞口。塔内表压为0.85at。水槽水面至塔内水出口处垂直高度差22m。已知水流量为42.5m3/h,泵对水作的有效功为321.5J/kg,管路总长110m(包括局部阻力当量管长),管子内径100mm。试计算摩擦系数λ值。解:1--1与2--2间列柏努利方程:gz1+u12/2+p1/r+Ws=gz2+u22/2+p2/r+Shfz1=0,z2=22m,u1=0,p1(表)=0u2==42.5/(´0.12´3600)=1.50m/s p2=0.85at=0.85´9.81´104=8.34´104PaWs=gz2+u12/2+p2/r+Shf即321.5=9.81´22+1.502/2+8.34´104/103+ShfShf=21.2J/kgShf=u2/2=´1.502/2=21.2l=0.017122 11
41.35℃的水由高位槽经异径收缩管向下流动。如图。若不考虑流动阻力,为保证水在流经收缩管时不发生汽化现象,收缩管的管径应限制在多大尺寸以上?当地大气压为1atm,35℃的水的密度为994kg/m3,饱和蒸汽压为5.62kPa。H=12m,h=8m,d=150mm(内直径)。11 22Hhd3 3习题41附图解:1]“1--1”至“3--3”列柏努利方程gz1+p1/r+u12/2=gz3+p3/r+u32/2∵p1=p3,z3=0,u1=0u3===15.3m/s2]“2--2”至“3--3”列柏努利方程gz2+p2/r+u22/2=gz3+p3/r+u32/22截面刚液体汽化时,p2=5.62kPa,则9.81´8+5.62´103/994+u22/2=1.013´105/994+15.32/2u2=16.4m/s3]∵u3d32=u2d22即15.3´1502=16.4d22d2=145mm42.如附图所示,水泵抽水打进B、C水槽。已知各管内径相等,且A—B段、A—C段和OA段(不包括泵内阻力)的管道长与局部阻力当量管长之和相等。设摩擦系数λ值皆相同,过程定态。求。C水BVCA水VB8.0m5.0m O习题42附图解:由“A®B”与“A®C”可列下式EA-EC=aVC2EA-EB=aVB2EC-EB=a(VB2-VC2)代入数据:9.81´(8.0-5.0)=a(VB2-VC2)即:29.4=a(VB2-VC2)……(1)
由“O®B”得Ws=EB+a(VC+VB)2+aVB2代入数据:150=9.81´5.0+a(VC+VB)2+aVB2即:101=a(VC+VB)2+aVB2……(2)(2)/(1),得[(VC+VB)2+VB2]/(VB2-VC2)=[(VC/VB+1)2+1]/[1-(VC/VB)2]解得:VC/VB=0.38743.在φ108×4mm的圆直管内用毕托管测点流速。已知管内流体是平均分子量为35的混合气体,压强为200mmH2O(表压),外界大气压为1atm,气温为32℃,气体粘度为0.02cP。在测管轴心处vmax时,U形压差计读数R为10mm,压差计指示液为水。问:管内气体流量是多少m3/h?44.在内径为50mm的圆直管内装有孔径为25mm的孔板,管内流体是25℃清水。按标准测压方式以U形压差计测压差,指示液为汞。测得压差计读数R为500mm,求管内水的流量。45.某转子流量计,刻度是按常压、20℃空气实测确定的。现用于测常压下15℃的氯气,读得刻度为2000。已知转子的密度为2600kg/m3,问:氯气流量多少?46.已知某容器的容积V=0.05m3,内储压缩空气,空气密度为8.02kg/m3。如图。在打开阀门时,空气以285m/s流速冲出,出口面积A=65mm2。设容器内任一时刻空气性质是均匀的。外界大气密度为1.2kg/m3。求打开阀门的瞬时容器内空气密度的相对变化率。
第二章流体输送机械1)某盛有液体的圆筒容器,容器轴心线为铅垂向,液面水平,如附图中虚线所示。当容器以等角速度ω绕容器轴线旋转,液面呈曲面状。试证明:①液面为旋转抛物面。②。③液相内某一点(r,z)的压强。式中ρ为液体密度。解题给条件下回旋液相内满足的一般式为(常量)取圆柱坐标如图,当Z=0,r=0,P=P0,∵C=P0故回旋液体种,一般式为①① 液面为P=P0的等压面,为旋转抛物面②又即:h0=∴H=2h0③某一点(r,Z)的压强P:
2)直径0.2m、高0.4m的空心圆桶内盛满水,圆筒定该中心处开有小孔通大气,液面与顶盖内侧面齐平,如附图所示,当圆筒以800rpm转速绕容器轴心线回旋,问:圆筒壁内侧最高点与最低点的液体压强各为多少?解取圆柱坐标如图,当Z=0,r=0,P=P0,∴C=P0故回旋液体种,一般式为 B点:Z=0,r=R=0.1m,C点:Z=-0.4m,r=0.1m,3)以碱液吸收混合器中的CO2的流程如附图所示。已知:塔顶压强为0.45at(表压),碱液槽液面与塔内碱液出口处垂直高度差为10.5m,碱液流量为10m3/h,输液管规格是φ57×3.5mm,管长共45m(包括局部阻力的当量管长),碱液密度,粘度,管壁粗糙度。试求:①输送每千克质量碱液所需轴功,J/kg。②输送碱液所需有效功率,W。解①,查得∴②
4)在离心泵性能测定试验中,以2泵汲入口处真空度为220mmHg,以孔板流量计及U形压差计测流量,孔板的孔径为35mm,采用汞为指示液,压差计读数,孔流系数,测得轴功率为1.92kW,已知泵的进、出口截面间的垂直高度差为0.2m。求泵的效率η。解5)IS65-40-200型离心泵在时的“扬程~流量”数据如下:V m3/h7.512.515He m13.212.511.8用该泵将低位槽的水输至高位槽。输水管终端高于高位槽水面。已知低位槽水面与输水管终端的垂直高度差为4.0m,管长80m(包括局部阻力的当量管长),输水管内径40mm,摩擦系数。试用作图法求工作点流量。Vm3/h7.512.515H’em9.6019.526.4Hem13.212.511.8由作图法得,工作点流量V=9.17m3/h6)IS65-40-200型离心泵在时的“扬程~流量”曲线可近似用如下数学式表达:,式中He为扬程,m,V为流量,m3/h。试按第5题的条件用计算法算出工作点的流量。
[解]7)某离心泵在时的“扬程~流量”关系可用表示,式中He为扬程,m,V为流量,m3/h。现欲用此型泵输水。已知低位槽水面和输水管终端出水口皆通大气,二者垂直高度差为8.0m,管长50m(包括局部阻力的当量管长),管内径为40mm,摩擦系数。要求水流量15m3/h。试问:若采用单泵、二泵并连和二泵串联,何种方案能满足要求?略去出口动能。8)有两台相同的离心泵,单泵性能为,m,式中V的单位是m3/s。当两泵并联操作,可将6.5l/s的水从低位槽输至高位槽。两槽皆敞口,两槽水面垂直位差13m。输水管终端淹没于高位水槽水中。问:若二泵改为串联操作,水的流量为多少?9)承第5题,若泵的转速下降8%,试用作图法画出新的特性曲线,并设管路特性曲线不变,求出转速下降时的工作点流量。[解]设原来转速为n,后来转速n’=0.92n,前后各有关参量的关系为:
可由原来的(He,V)数据一一对应算出新转速时的(H’eV’)数据,如下表所示:转速nVm3/h7.512.515Hem13.212.511.8转速n’V’m3/h6.911.513.8H’em11.1710.589.99管路特性曲线:He=4.0+0.0995V2m,(V—m3/h),可作图法得(V,He’’),数据如下:(6.9,8.74),(11.5,17.16),(13.3,22.9)由作图法得,工作点V=8.8m3/h10)用离心泵输送水,已知所用泵的特性曲线方程为:。当阀全开时的管路特性曲线方程:(两式中He、He’—m,V—m3/h)。问:①要求流量12m3/h,此泵能否使用?②若靠关小阀的方法满足上述流量要求,求出因关小阀而消耗的轴功率。已知该流量时泵的效率为0.65。解:(1)He=36-0.02V2He‘=12+0.06V2∵He=He’,解得V=17.3m3/h适用(2)当V=12m3/hHe=36-0.02´122=33.12m,He‘=12+0.06V2=12+0.06´122=20.64m11)用离心泵输水。在n=2900r/min时的特性为He=36-0.02V2,阀全开时管路特性为He’=12+0.06V2(两式中He、He’--m,V--m3/h)。试求:①泵的最大输水量;②要求输水量为最大输水量的85%,且采用调速方法,泵的转速为多少?解:(1)He=36-0.02V2He’=12+0.06V2∵He=He’,解得V=17.3m3/h(2)V’=0.85V=14.7m3/h,令调速后转速为nr/minH’=()2HV’=泵:(29002/n2)H’=36-0.02´(29002/n2)V’2H’=36´n2/(29002)-0.02V’2当V=14.7m3/h则H’=(n2/29002)´36-0.02´14.72He’=12+0.06V’2=12+0.06´14.72=24.97m由He=He’,解得n=2616r/min 12)用泵将水从低位槽打进高位槽。两槽皆敞口,液位差55m。管内径158mm。当阀全开时,管长与各局部阻力当量长度之和为1000m。摩擦系数0.031。泵的性能可用He=131.8-0.384V表示(He--m,V--m3/h)。试问:①要求流量为110m3/h,选用此泵是否合适?②若采用上述泵,转速不变,但以切割叶轮方法满足110m3/h流量要求,以D、D’分别表示叶轮切割前后的外径,问D’/D为多少?解:(1)管路He=H0+KV2=Dz+[8l(l+Sle)/(p2gd5)]Vs2=55+2.601´104Vs2=55+0.00201V2=55+[8´0.031´1000/(p2´9.81´0.1585)]Vs2
由He=131.8-0.384VHe=55+0.00201V2得V=122.2m3/h>110m3/h适用(2)H=(D/D’)2H’V=(D/D’)V’切削叶轮后:(D/D’)2H’=131.8-0.384(D/D’)V’即H’=(D’/D)2´131.8-0.384(D’/D)V’V=110m3/h时,H’=(D’/D)2´131.8-0.384(D’/D)V’=(D’/D)2´131.8-0.384(D’/D)´110=131.8(D’/D)2-42.24(D’/D)He’=55+0.00201V’2=55+0.00201´1102=79.32m,由He’=H’,解得D’/D=0.952 13)某离心泵输水流程如附图示。泵的特性曲线方程为:He=42-7.8´104V2(He--m,V--m3/s)。图示的p为1kgf/cm2(表)。流量为12L/s时管内水流已进入阻力平方区。若用此泵改输r=1200kg/m3的碱液,阀开启度、管路、液位差及P值不变,求碱液流量和离心泵的有效功率。习题13附图解:p=1kgf/cm2=9.807´104PaV=12L/s=0.012m3/s管路He’=H0+KV2=10+(9.807´104)/(9.807´1000)+KV2=20+K´0.0122He=42-7.8´104´0.0122=30.77m∵He=He’K=7.48´104∵改输碱液阀门开度、管路不变K=7.48´104不变管路:He’=Dz+p/(rg)+KV2=10+9.81´104/(9.81´1200)+7.48´104V2=18.33+7.48´104V2泵He=42-7.8´104V2∵He=He’,解得:V=0.0124m3/s∵He=42-7.8´104V2=42-7.8´104´0.01242=30.0mNe=HegVr=30.0´9.81´0.0124´1200=4.38´103W14)某离心泵输水,其转速为2900r/min,已知在本题涉及的范围内泵的特性曲线可用方程He=36-0.02V来表示。泵出口阀全开时管路特性曲线方程为:He’=12+0.05V2(两式中He、He’¾m,V¾m3/h)。①求泵的最大输水量。②当要求水量为最大输水量的85%时,若采用库存的另一台基本型号与上述泵相同,但叶轮经切削5%的泵,需如何调整转速才能满足此流量要求?解:(1)由He=36-0.02VHe’=12+0.05V2令He=He’解得V=21.71m3/h(2)D’/D=0.95V’=0.85V=0.85´21.71=18.45m3/h另一泵:He=36´0.952-0.02´0.95V=32.49-0.019V调整转速后:He=32.49(n/2900)2-0.019(n/2900)V=32.49(n/2900)2-0.019(n/2900)´18.45=32.49(n/2900)2-0.351(n/2900)又He’=12+0.05V2=12+0.05´18.452=29.02m,由He=He’解得n=2756r/min15)某离心泵输水流程如图示。水池敞口,高位槽内压力为0.3at(表)。该泵的特性曲线方程为:He=48-0.01V2(He¾m,V¾m3/h)。在泵出口阀全开时测得流量为30m3/h。现拟改输碱液,其密度为1200kg/m3,管线、高位槽压力等都不变,现因该泵出现故障,换一台与该泵转速及基本型号相同但叶轮切削5%的离心泵进行操作,问阀全开时流量为多少?
解:p=0.3at=2.94´104Pa管路He’=Dz+p/(rg)+KV2=20+2.94´104/(9.81´1000)+KV2=23+KV2V=30m3/h时He=48-0.01V2=48-0.01´302=39m习题15附图He’=23+KV2=23+K´302由于He=He’K=0.0178管路He’=23+0.0178V2泵:He=48´(D’/D)2-0.01V2=48´0.952-0.01V2=43.32-0.01V2改泵后管路:He’=Dz+p/(rg)+KV2=20+2.94´104/(9.81´1200)+0.018V2=22.5+0.018V2He=43.32-0.01V2He‘=22.5+0.018V2得V=27.3m3/h 14)IS100-80-160型离心泵,P0=8.6mH2O,水温150C,将水由低位槽汲入泵,有管路情况基本的性能,知V=60m3/h,查的△h,允=3.5m,已知汲入管阻力为2.3m,H2O,求最大安装高度[解]150C清水:ρ=9999kg./m3,PV=1705.16Pa15)100KY100-250型离心泵,P0=8.6mH2O,水温150C,将水由低位槽汲入泵,已知工作点流量为100m3/h,查得[HS]=5.4m,汲水管内径为100mm,汲水管阻力为5.4mH2O。求Hg,max18)大气状态是10℃、750mmHg(绝压)。现空气直接从大气吸入风机,然后经内径为800mm的风管输入某容器。已知风管长130m,所有管件的当量管长为80m,管壁粗糙度,空气输送量为2×104m3/h(按外界大气条件计)。该容器内静压强为1.0×104Pa(表压)。库存一台9-26型No.8离心式风机,,当流量为21982m3/h,mmH2O,其出风口截面为0.392×0.256m2。问:该风机能否适用?
19)离心式风机输送空气,由常压处通过管道水平送至另一常压处。流量6250kg/h。管长1100m(包括局部阻力),管内径0.40m,摩擦系数0.0268。外界气压1kgf/cm2,大气温度20℃,。若置风机于管道出口端,试求风机的全风压。[提示:1.风管两端压力变化(p1-p2)/p1<20%时,可视为恒密度气体,其rM值按平均压力(p1+p2)/2计算。2.为简化计算,进风端管内气体压力视为外界气压。3.管道两端压差<104Pa]解:以下以H表示管路的压降(p1-p2)。∵pm=[p0+(p0-H)]/2=p0-H/2rm=pm·M/(RT)=(p0-H/2)M/(RT)H=l(l/d)(u2/2)rm=l(l/d)(rmu)2/(2rm)=llW2/{[(p/4)d2]22drm}=8llW2RT/[p2d5(p0-H/2)M]令C=8llW2RT/(p2d5M)则上式为H2-2p0H+2C=0其中C=8´0.0268´1100´(6250/3600)2´8314´293.2/(p2´0.405´29)=5.912´108由H2-(2´9.81´104)H+(2´5.912´108)=0解得H=6222Pa校核:H/p1=6222/(9.81´104)=0.063<0.20,把气体密度视为常量是可以的。则风机的全风压H全=H=6222Pa 20)离心泵、往复泵各一台并联操作输水。两泵“合成的”性能曲线方程为:He=72.5-0.00188(V-22)2,V指总流量。阀全开时管路特性曲线方程为:He’=51+KV2,(两式中:He、He’--mH2O,V--L/s)。现停开往复泵,仅离心泵操作,阀全开时流量为53.8L/s。试求管路特性曲线方程中的K值。解:只开离心泵时He=72.5-0.00188V2V=53.8L/s时He=72.5-0.00188V2=72.5-0.00188´53.82=67.06mHe’=51+KV2=51+K´53.82∵He=He’K=0.00555m/(L/s)2
第四章传热及传热器1)用平板法测定材料的导热系数,其主要部件为被测材料构成的平板,其一侧用电热器加热,另一侧用冷水将热量移走,同时板的两侧用热电偶测量其表面温度。设平板的导热面积为0.03m2,厚度为0.01m。测量数据如下:电热器材料的表面温度 ℃安培数A伏特数V高温面低温面2.82.314011530020010050试求:①该材料的平均导热系数。②如该材料导热系数与温度的关系为线性:,则λ0和a值为多少?2)通过三层平壁热传导中,若测得各面的温度t1、t2、t3和t4分别为500℃、400℃、200℃和100℃,试求合平壁层热阻之比,假定各层壁面间接触良好。3)某燃烧炉的平壁由耐火砖、绝热砖和普通砖三种砌成,它们的导热系数分别为1.2W/(m·℃),0.16W/(m·℃)和0。92W/(m·℃),耐火砖和绝热转厚度都是0.5m,普通砖厚度为0.25m。已知炉内壁温为1000℃,外壁温度为55℃,设各层砖间接触良好,求每平方米炉壁散热速率。4)在外径100mm的蒸汽管道外包绝热层。绝热层的导热系数为0.08W/(m·℃),已知蒸汽管外壁150℃,要求绝热层外壁温度在50℃以下,且每米管长的热损失不应超过150W/m,试求绝热层厚度。
5)Φ38×2.5mm的钢管用作蒸汽管。为了减少热损失,在管外保温。50第一层是mm厚的氧化锌粉,其平均导热系数为0.07W/(m·℃);第二层是10mm厚的石棉层,其平均导热系数为0.15W/(m·℃)。若管内壁温度为180℃,石棉层外表面温度为35℃,试求每米管长的热损失及两保温层界面处的温度?解:①r0=16.5mm=0.0165m,r1=19mm=0.019mr2=r1+d1=0.019+0.05=0.069mr3=r2+d2=0.069+0.01=0.079ml0=45W/(m·℃)W/m②即∴t2=41.8℃6)通过空心球壁导热的热流量Q的计算式为:,其中,A1、A2分别为球壁的内、外表面积,试推导此式。7)有一外径为150mm的钢管,为减少热损失,今在管外包以两层绝热层。已知两种绝热材料的导热系数之比1,两层绝热层厚度相等皆为30mm。试问应把哪一种材料包在里层时,管壁热损失小。设两种情况下两绝热层的总温差不变。
8)试用因次分析法推导壁面和流体间强制对流给热系数α的准数关联式。已知α为下列变量的函数:。式中λ、CP、ρ、μ分别为流体的导热系数、等压热容、密度、粘度,u为流体流速,l为传热设备定型尺寸。9)水流过φ60×3.5mm的钢管,由20℃被加热至60℃。已知,水流速为1.8m/s,试求水对管内壁的给热系数。10)空气流过φ36×2mm的蛇管,流速为15m/s,从120℃降至20℃,空气压强4×105Pa(绝压)。已知蛇管的曲率半径为400mm,,试求空气对管壁的给热系数。空气的密度可按理想气体计算,其余物性可按常压处理。
11)苯流过一套管换热器的环隙,自20℃升至80℃,该换热器的内管规格为φ19×2.5mm,外管规格为φ38×3mm。苯的流量为1800kg/h。试求苯对内管壁的给热系数。12)冷冻盐水(25%的氯化钙溶液)从φ25×2.5mm、长度为3m的管内流过,流速为0.3m/s,温度自-5℃升至15℃。假设管壁平均温度为20℃,试计算管壁与流体之间的平均对流给热系数。已知定性温度下冷冻盐水的物性数据如下:密度为1230kg/m3,粘度为4×10-3Pa·s,导热系数为0.57W/(m·℃),比热为2.85kJ/(kg·℃)。壁温下的粘度为2.5×10-3Pa·s。解:d=0.025-0.0025×2=0.02m∴>50∵u=0.3m/s∴<2000∴层流>100=354.7W/(m2×℃)13)室内分别水平放置两根长度相同,表面温度相同的蒸汽管,由于自然对流两管都向周围散失热量,已知小管的,大管直径为小管的8倍,试求两管散失热量的比值为多少?解:∵小管Gr×Pr=108∴b=1/3又因Gr∝d03,故大管Gr×Pr>108则14)某烘房用水蒸汽通过管内对外散热以烘干湿纱布。已知水蒸汽绝压为476.24kPa,设管外壁温度等于蒸汽温度现室温及湿纱布温度均为20℃,试作如下计算:①使用一根2m长、外径50mm水煤气管,管子竖直放于水平放置单位时间散热量为多少?②若管子水平放置,试对比直径25mm和50mm水煤气管的单位时间单位面积散热之比。(管外只考虑自然对流给热)。
15)油罐中装有水平蒸汽管以加热管内重油,重油温度为20℃,蒸汽管外壁温为120℃,在定性温度下重油物性数据如下:密度为900kg/m3,比热1.88×103J/(kg·℃),导热系数为0.175W/(m·℃),运动粘度为2×10-6m2/s,体积膨胀系数为3×10-4l/℃,管外径为68mm,试计算蒸汽对重油的传热速度W/m2。16)有一双程列管换热器,煤油走壳程,其温度由230℃降至120℃,流量为25000kg/h,内有φ25×2.5mm的钢管70根,每根管长6m,管中心距为32mm,正方形排列。用圆缺型挡板(切去高度为直径的25%),试求煤油的给热系数。已知定性温度下煤油的物性数据为:比热为2.6×103J/(kg·℃),密度为710kg/m3,粘度为3.2×10-4Pa·s,导热系数为0.131W/(m·℃)。挡板间距,壳体内径。
17)饱和温度为100℃的水蒸汽在长为2.5m,外径为38mm的竖直圆管外冷凝。管外壁温度为92℃。试求每小时蒸汽冷凝量。又若将管子水平放置每小时蒸汽冷凝量又为多少。18)由φ25×2.5mm、225根长2米的管子按正方形直列组成的换热器,用1.5×105Pa的饱和蒸汽加热某液体,换热器水平放置。管外壁温度为88℃,试求蒸汽冷凝量。
19)设有A、B两平行固体平面,温度分别为TA和TB(TA>TB)。为减少辐射散热,在这两平面间设置n片很薄的平行遮热板,设A所有平面的表面积相同,黑度相等,平板间距很小,试证明设置遮热板后A平面的散热速率为不装遮热板时的倍。20)用热电偶测量管内空气温度,测得热电偶温度为420℃,热电偶黑度为0.6,空气对热电偶的给热系数为35W/(m·℃),管内壁温度为300℃,试求空气温度。21)外径为60mm的管子,其外包有20mm厚的绝热层,绝热层材料导热系数为0.1W/(m·℃),管外壁温度为350℃,外界温度为15℃,试计算绝热层外壁温度。若欲使绝热层外壁温度再下降5℃,绝热层厚度再增加多少。
22)设计一燃烧炉,拟用三层砖,即耐火砖、绝热砖和普通砖。耐火砖和普通砖的厚度为0.5m和0.25m。三种砖的系数分别为1.02W/(m·℃)、0.14W/(m·℃)和0.92W/(m·℃),已知耐火砖内侧为1000℃,外壁温度为35℃。试问绝热砖厚度至少为多少才能保证绝热砖温度不超过940℃,普通砖不超过138℃。23)为保证原油管道的输送,在管外设置蒸汽夹。对一段管路来说,设原油的给热系数为420W/(m·℃),水蒸气冷凝给热系数为104W/(m·℃)。管子规格为φ35×2mm钢管。试分别计算Ki和K0,并计算各项热阻占总热阻的分率。24)某列管换热器,用饱和水蒸汽加热某溶液,溶液在管内呈湍流。已知蒸汽冷凝给热系数为104W/(m·℃),单管程溶液给热系数为400W/(m·℃),管壁导热及污垢热阻忽略不计,试求传热系数。若把单管程改为双管程,其它条件不变,此时总传热系数又为多少?
25)一列管换热器,管子规格为φ25×2.5mm,管内流体的对流给热系数为100W/(m·℃),管外流体的对流给热系数为2000W/(m·℃),已知两流体均为湍流流动,管内外两侧污垢热阻均为0.0018m·℃/W。试求:①传热系数K及各部分热阻的分配;②若管内流体流量提高一倍,传热系数有何变化?③若管外流体流量提高一倍,传热系数有何变化?解:①Ri=R0=0.00118m2×℃/W钢管l=45W/(m×℃)m=0.015421/(W/m2℃)K0=64.84W/(m2×℃)热阻分配:污垢:管外:管内:管壁:②,,∴=0.01010m2℃/WW/(m2℃)
③,∴=0.01521m2℃/WW/(m2℃)
31)120℃饱和水蒸汽将空气从20℃加热至80℃,空气流量1.20×104kg/h。现有单程列管换热器,f25×2.5mm钢管300根,管长3m,a0=104W/(m2℃),污垢及管壁热阻不计。问此换热器能否满足要求。解:℃50℃空气,r=1.093kg/m3,Cp=1.005kJ/(kg×℃),l=0.02824W/(m×℃)m=1.96×10-5Pa×s,Pr=0.698m/s>10000∴W/(m2℃)∵a0>>ai∴Ki=ai=124.5W/(m2℃)Q=WcCpcDt=×1.005×60=201kJ/sDtm=℃Q=KiAiDtm即201×103=124.5Ai×65.5∴Ai=24.6m2又,Ai=npdiL即24.6=300p×0.020L∴L=1.31m<3m∴满足要求32)某单壳程单管程列管换热器,用1.8×105Pa饱和水蒸汽加热空气,水蒸汽走壳程,其给热系数为105W/(m·℃),空气走管内,进口温度20℃,要求出口温度达110℃,空气在管内流速为10m/s。管子规格为φ25×2.5mm的钢管,管数共269根。试求换热器的管长。
若将该换热器改为单壳程双管程,总管数减至254根。水蒸汽温度不变,空气的质量流量及进口温度不变,设各物性数据不变,换热器的管长亦不变,试求空气的出口温度。33)一套管换热器,用热柴油加热原油,热柴油与原油进口温度分别为155℃和20℃。已知逆流操作时,柴油出口温度50℃,原油出口60℃,若采用并流操作,两种油的流量、物性数据、初温和传热系数皆与逆流时相同,试问并流时柴油可冷却到多少温度?
34)一套管换热器,冷、热流体的进口温度分别为55℃和115℃。并流操作时,冷、热流体的出口温度分别为75℃和95℃。试问逆流操作时,冷、热流体的出口温度分别为多少?假定流体物性数据与传热系数均为常量。35)一列管换热器,管外用2.0×105Pa的饱和水蒸汽加热空气,使空气温度从20℃加热到80℃,流量为20000kg/h,现因生产任务变化,如空气流量增加50%,进、出口温度仍维持不变,问在原换热器中采用什么方法可完成新的生产任务?
’36)在一单管程列管式换热器中,将2000kg/h的空气从20℃加热到80℃,空气在钢质列管内作湍流流动,管外用饱和水蒸汽加热。列管总数为200根,长度为6m,管子规格为φ38×3mm。现因生产要求需要设计一台新换热器,其空气处理量保持不变,但管数改为400根,管子规格改为φ19×1.5mm,操作条件不变,试求此新换热器的管子长度为多少米?37)在单程列管换热器内,用120℃的饱和水蒸汽将列管内的水从30℃加热到60℃,水流经换热器允许的压降为3.5Pa。列管直径为φ25×2.5mm,长为6m,换热器的热负荷为2500kW。试计算:①列管换热器的列管数;②基于管子外表面积的传热系数K。假设:列管为光滑管,摩擦系数可按柏拉修斯方程计算,。解:(1)℃45℃时水:r=990kg/m3,Cp=4.174×103J/(kg℃),l=64.03×10-2W/(m℃)m=60.12×10-5Pa×s,Pr=3.925
∴u=1.00m/s℃设管壁及污垢热阻可略∵a0>>ai∴Ki=ai对一根管,=3.895×104W又,即3.895´104=5.23´103´p´0.02´6´73.99∴=1.117×103W/(m2×℃)(2)∴取n为64根。38)有一立式单管程列管换热器,其规格如下:管径φ25×2.5mm,管长3m,管数30根。现用该换热器冷凝冷却CS2饱和蒸汽,从饱和温度46℃冷却到10℃。CS2走管外,其流量为250kg/h,冷凝潜热为356kJ/kg,液体CS2的比热为1.05kJ/(kg·℃)。水走管内与CS2呈逆流流动,冷却谁进出温度分别为5℃和30℃。已知CS2冷凝和冷却时传热系数(以外表面积计)分别为和。问此换热器是否合用?解:kJ/s设换热器上部为蒸汽冷凝段,以下标“1”表示,下部为冷却段,以“2”表示则kJ/sT1=46℃kJ/st2=30℃Q1Q2T2=10℃设冷水Cp为常量,则上下两段分界处t3:t3t1=5℃即∴t3=7.4℃于是:m2m2
∴A=A1+A2=4.14+1.37=5.51m2(以外表面积计)现有换热器A'=npd0L=30´p´0.025´3=7.07m2>A故能适用。 39)现有两台规格完全一样的列管换热器,其中一台每小时可以将一定量气体自80℃冷却到60℃,冷却水温度自20℃升到30℃,气体在管内与冷却水呈逆流流动,已知总传热系数(以内表面积为基准)Ki为40W/(m·℃)。现将两台换热器并联使用,忽略管壁热阻、垢层热阻、热损失及因空气出口温度变化所引起的物性变化。试求:①并联使用时总传热系数;②并联使用时每个换热器的气体出口温度;③若两换热器串联使用,其气体出口温度又为多少(冷却水进出每个换热器的温度不变)?解:单台:Wh×Cph(T1-T2)=Wc×Cpc(t2-t1)∴Wh×Cph(T1-T2)=Ki×Ai×Dtm,℃∴二台并联:W/(m2×℃)即……①又…………………………………………②由①、②式联立,解得T2¢=57.6℃,t2¢=31.2℃二台串联:即:………③又:……………………………………………④③、④式联立,解得:T2¢=48.2℃,t2¢=35.9℃
40)拟设计一台列管换热器,20kg/s的某油品走壳程,温度自160℃降至115℃,热量用于加热28kg/s的原油。原油进口温度为25℃,两种油的密度均为870kg/m3。其他物性数据如下:名称CP kJ/(kg·℃)μ Pa·sλ W/(m·℃)原油油品1.992.202.9×10-35.2×10-30.1360.119解:(略)第七章液体蒸馏1)1) 苯酚(C6H5OH)(A)和对甲酚(C6H4(CH3)OH)(B)的饱和蒸汽压数据为:温度℃苯酚蒸汽压kPa对甲酚蒸汽压kPa温度℃苯酚蒸汽压kPa对甲酚蒸汽压kPa113.710.07.70117.811.999.06114.610.47.94118.612.439.39115.410.88.2119.412.859.70116.311.198.5120.013.2610.0117.011.588.76 试按总压P=75mmHg(绝压)计算该物系的“t—x—y”数据。此物系为理想物系。t0CpA0kPapB0kPaxAxB113.710.07.701.01.0114.610.47.940.8370.871115.410.88.20.6920.748116.311.198.50.5580.624117.011.588.760.4400.509117.811.999.060.3210.385118.612.439.390.2010.249119.412.859.700.09520.122120.013.2610.00.0000.0002)承第1题,利用各组数据,计算①在x=0至x=1范围内各点的相对挥发度αi,取各αi的算术平均值α,算出α对αi的最大相对误差。②以平均α作为常数代入平衡方程式算出各点的“y—xi”关系,算出由此法得出各组yi值的最大相对误差。113.7114.6115.4116.3117.0117.8118.6119.4120.0
t0C1.2991.3101.3171.3161.3221.3231.3241.3251.326t0C113.7114.6115.4116.3117.0117.8118.6119.4120.0xi1.00.8370.6920.5580.4400.3210.2010.09520yi1.00.8710.7480.6250.5090.3840.2490.1220最大误差=3)已知乙苯(A)与苯乙烯(B)的饱和蒸汽压与温度的关系可按下式算得:式中p0的单位是mmHg,T的单位是K。问:总压为60mmHg(绝压)时,A与B的沸点各为多少℃?在上述总压和65℃时,该物系可视为理想物系。此物系的平衡汽、液相浓度各为多少摩尔分率? 4)苯(A)和甲苯(B)混合液可作为理想溶液,其各纯组分的蒸汽压计算式为
式中p0的单位是mmHg,t的单位是℃。试计算总压为850mmHg(绝压)下含苯25%(摩尔百分率)的该物系混合液的泡点。5)试计算总压为760mmHg(绝压)下,含苯0.37、甲苯0.63(摩尔分率)的混合蒸汽的露点。若令该二元物系降温至露点以下3℃,求平衡的汽、液相摩尔之比。
6)有一苯(A)、甲苯(B)、空气(C)的混合气体,其中空气占2%,苯与甲苯浓度相等(均指摩尔百分数),气体压强为760mmHg(绝压)。若维持压强不变,令此三元物系降温至95℃,求所得平衡汽相的组成。A、B组分均服从拉乌尔定律。已知95℃时,。设XA0.380.3780.3770.376算得的X‘A0.3240.3520.3630.3737)常压下将含苯(A)60%,甲苯(B)40%(均指摩尔百分数)的混合液闪蒸(即平衡蒸馏),得平衡汽、液相,汽相摩尔数占总摩尔数的分率——汽化率(1-q)为0.30。物系相对挥发度α=2.47,试求:闪蒸所得平衡汽、液相的浓度。若改用简单蒸馏,令残液浓度与闪蒸的液相浓度相同,问:馏出物中苯的平均浓度为多少?提示:若原料液、平衡液、汽相中A的摩尔分率分别以xf、x、y表示,则存在如下关系:。
8)某二元物系,原料液浓度xf=0.42,连续精馏分离得塔顶产品浓度xD=0.95。已知塔顶产品中易挥发组分回收率η=0.92,求塔底产品浓度xw。以上浓度皆指易挥发组分的摩尔分率。9)某二元混合液含易挥发组分0.35,泡点进料,经连续精馏塔分离,塔顶产品浓度xD=0.96,塔底产品浓度xw=0.025(均为易挥发组分的摩尔分率),设满足恒摩尔流假设。试计算塔顶产品的采出率D/F。若回流比R=3.2,泡点回流,写出精馏段与提馏段操作线方程。10)某二元混合物含易挥发组分0.24,以热状态参数q=0.45的汽、液混合物状态进入连续精馏塔进行分离。进料量为14.5kmol/h,塔顶产品浓度xD=0.95,塔底产品浓度xw=0.03。若回流比R=2.8,泡点回流,提馏段L’/V’为多少?试计算塔顶全凝器的蒸汽冷凝量及蒸馏釜的蒸发量。以上浓度皆指易挥发组分的摩尔分率。
11)用常压精馏塔连续分离苯和甲苯混合液。进料中苯的摩尔分率为0.30。操作条件下苯的汽化潜热为355kJ/kg。试求以下各种情况下的q值:①进料温度为25℃;②98.6℃的液体进料;③98.6℃的蒸汽进料。苯~甲苯体系在常压下的部分汽液平衡数据如下:温度t,℃110.6102.298.695.2液相组成,x0.0000.2000.3000.397汽相组成,y0.0000.3700.5000.618解:①原料液的汽化潜热rm=0.30´380kJ/(1kg/78kg/mol)+=8892+22862=31754kJ/mol由附表可知xf=0.30时,液体的泡点为98.6℃,则平均温度℃=334.95K查教材附录得61.8℃下苯和甲苯的比热为1.84kJ/(kg×K),故原料液的比热为:Cp=1.84´0.3´78+1.84´0.7´92=161.552kJ/(kmol×K)∴②属饱和液体进料q2=1③属饱和蒸汽进料q3=0。12)已知某精馏塔操作以饱和蒸汽进料,操作线方程分别如下:精馏线提馏线试求该塔操作的回流比、进料组成及塔顶、塔底产品中轻组分的摩尔分率。解:由精馏线得:,R=2.500
由提馏线得:,xD=0.9499≈0.950提馏线斜率,得F=1.5D提馏线截距,,得xW=0.04由FxF=DxD+WxW得:=0.64713)用一连续精馏塔分离甲醇和水的混合物,进料量为100kmol/h,进料中甲醇的摩尔分率为0.10,以饱和蒸汽形式连续进入塔底。要求塔顶产品中甲醇含量为0.90,塔釜产品中甲醇含量为0.05。试求:①该精馏塔操作回流比及塔内的液汽比;②塔顶全凝器的蒸汽冷凝量。解:①Fxf=DxD+(F-D)xWkmol/hV=F=100kmol/hVLFxDxfq=0xw由V=(R+1)D得②塔顶全凝器蒸汽冷凝量V=100kmol/h 14)以连续精馏分离正庚烷(A)与正辛烷(B)。已知相对挥发度α=2.16,原料液浓度Zf=0.35(正庚烷的摩尔分率,下同),塔顶产品浓度xD=0.94,加料热状态q=1.05,馏出产品的采出率D/F=0.34。在确定回流比时,取。设泡点回流。试写出精馏段与提馏段操作线方程。
15)承第14题,按最佳加料板位置加料,试用作图法求总理论板数,并指明加料板的序号。解:又作图知,总理论板数为13.4块,第7块为加料板。(图略)16)承第14题,试用逐板计算法计算离开塔顶第2块塔板的液体浓度x2。解:17)承第14题,试用快速估算法计算总理论板数和确定加料板序号。解:(1)总理论板数
(2)精馏段理论板数18)以常压操作的连续精馏塔分离“乙醇~水”溶液。原料液含乙醇0.10(摩尔分率,下同),进料热状态q=1.10,塔顶产品浓度0.80,釜液浓度0.001。塔顶用全凝器,泡点回流,塔底用蒸馏釜,间接加热,操作回流比为最小回流比的2.0倍。试用作图法求总理论板数和确定加料板序号。解:根据教材附录数据作“y-x”图
19)已知塔顶、塔底产品及进料组成中苯的摩尔分率分别为:xD=0.98,xW=0.05,xF=0.60,泡点进料和回流,取回流比为最小回流比的1.5倍,体系的相对挥发度为2.47。试用捷算法计算苯和甲苯体系连续精馏理论塔板数。解:∵q=1∴xe=xf=0.6R=1.5Rmin=1.5×1.03=1.55查吉利兰图得:由芬斯克方程得:则N=14.3,取NT=15 20)用一连续精馏塔分离甲醇和水的混合物。已知原料中甲醇的摩尔分率为0.35,进料量为100kmol/h,泡点进料。塔顶馏出液中甲醇含量为0.95,塔底产品中甲醇浓度为0.04。操作回流比为1.5,泡点回流,间接蒸汽加热。用作图法求完成分离任务所需的理论塔板数,并计算甲醇的回收率和塔釜蒸发量。解:甲醇回收率由教材附录查得CH3OH~H2O的VLE数据,在x~y图上作出平衡曲线。精馏线截距为由(0.95,0.95)和(0,0.38)作出精馏线由q=1和(0.35,0.35)作出q线连接(xw,xw)和q线与精馏线的交点得提馏线,作图得理论板数NT=7块,加料位置为第5块理论板。kmol/h∵q=1-0=,故kmol/h21)在用作图法求理论板数时,可能遇到局部区域平衡线与操作线均为直线且两直线甚靠近,不易求准梯级数的情况。设平衡线为,操作线为,(K、C、a、b均为常数),试推导由操作线上x0至xN所需理论板数N的数学解析式。
22)在某二元混合物连续、基本型精馏操作的基础上,若进料组成及流量不变,总理论板数及加料板位置不变,塔顶产品采集比D/F不变。试考虑在进料热状态参数q增大,回流比R不变的情况下xD、xW和塔釜蒸发量的变化趋势。只需定性分析。23)以连续精馏塔分离某二元混合物。塔顶采用全凝器。已知:xD=0.90,D=0.02kmol/s,回流比R’=2.5,在操作中回流液有一定程度过冷。已知回流液体泡点为83℃,汽化潜热r=3.2×104kJ/kmol,该液体比热CP=140kJ/(kmol·℃),但回流液温度为75℃。试求精馏段操作线方程。解:
24)以连续精馏塔分离某二元混合物。进料xf=0.50(摩尔分率,下同),q=1,塔顶产品D=50kmol/h,xD=0.95,塔顶馏出液中易挥发组分回收率η=0.96。塔顶采用一个分凝器及一个全凝器。分凝器液体泡点回流。已知回流液浓度x0=0.88,离开第一块塔板的液相浓度x1=0.79。塔底间接蒸汽加热。塔板皆为理论板,相对挥发度α为常数。试求:①加料流量F;②操作回流比是Rmin的倍数;③精馏段、提馏段气相流量。25)在常压下用一连续精馏塔分离某两组分混合液,已知进料量为200kmol/h,其中轻组分的含量为0.40(摩尔分率),泡点进料。塔顶产品流量为100kmol/h。体系在常压下的相对挥发度为2.6。若精馏塔的理论塔板数为无限多,试求:①当回流比为1.0时,塔顶、塔底产品中轻组分的含量各为多少?②当回流比为2.0时,塔顶、塔底产品中轻组分的含量各为多少?③画出两种情况下的精馏段、提馏段操作线和q线示意图。解:①由于NT=¥,设xq、yq达到相平衡,则R=Rmin=1.0∵q=1,∴xq=xf=0.4由,由物料衡算得:>0∴假设正确,计算有效。②R=2.0,设此时在xq、yq处达到相平衡
<0假设不成立,显然在xw=0处达到平衡,此时③NT=∞,R=1.0时,精馏段截距:NT=∞,R=2.0时,精馏段截距:y0.267xw=0xf=0.4xD=0.8xNT=∞,R=2.0y0.371xq,yqxw=0.058,xf=0.4xD=0.742xNT=∞,R=1.0 26)某一精馏塔有4块理论板(含塔釜)用来分离苯—甲苯混合物。进料量为100kmol/h,其中轻组分的含量为0.40(摩尔分率),以泡点状态连续加入到第三块板上(从塔顶数起)。塔顶产品的流量为20kmol/h,泡点回流操作回流比R=2.8。已知体系的相对挥发度为2.47。求塔顶和塔底产品的组成。(提示:用xW=0.2878作为试差初值)解:W=F-D=80kmol/h设=0.2878,则=0.8488精馏线y2=0.7368x1+0.2234=0.7368×0.6944+0.2234=0.7350y3=0.7368x2+0.2234=0.6131∵x3=0.3908<xf=0.4,改用提馏线与平衡线计算kmol/h∴提馏线
=2.0526x-0.3029y4=yw=2.0526x3-0.3029=2.0526×0.3908-0.3029=0.4993xD123Fxfx4=xwy4=ywy1y2y3x1x2x3xw与假设值=0.2878非常接近,相对误差为0.07%,故假设正确,∴xD=0.8488xw=0.2878 27)在常压连续回收塔中分离甲醇~水混合溶液。进料组成为0.10(摩尔分率),要求塔顶产品中甲醇的回收率为0.90,塔底直接水蒸汽加热。试求:①当塔板数为无穷多时,塔顶、塔底产品组成及每摩尔进料消耗的水蒸汽量;②若蒸汽用量为最小用量的两倍时,完成分离任务时所需理论板数及塔顶、塔底产品组成。常压下甲醇~水体系部分汽液平衡数据列于下表:液相组成x0.0000.0600.0800.100汽相组成y0.0000.3040.3650.418解:①Smin=DF=W,由Fxf=DxD+Wxw得Wxw=Fxf-DxD=Fxf(1-h)=0.1Fxf∵F=W∴xw=0.1xf=0.1×0.1=0.01∵NT=∞,故在塔顶进料处,xf与xD达相平衡,D,xD123F,xfxw,Wy1y2y3x1x2x3S由VLE数据表得xD=0.418全塔物料衡算Fxf+S×0=DxD+WxwFxf=S×xD+0.1FxfS×xD=0.9Fxf∴②由上面计算可知xw=0.01(此值由回收率而定)F×xf+S×0=D×xD+W×xw∵S=DF×xf=S×xD’+W×xw∴
Smin2SminxwxfxD’xD(注:当S=2Smin时,xf与xD不达相平衡)斜率点(xw,0)和点(xf,xD’)都在提馏线上,故提馏线斜率:截距∴提馏线:y=2.322x-0.0233要逐板计算,必须要有a,而a由下列方法获得,由本题附表可知:∴∴y2=2.322x1-0.0233=0.0656y3=2.322x2-0.0233=0.00108x3<xw=0.01∴(含釜)28)有两股丙酮(A)与水(B)的混合物分别加入塔内进行连续精馏分离。第一股进料摩尔流量为F1,q1=1,xf,1=0.80(摩尔分率,下同),在塔的上部加入;第二股进料摩尔流量为F2,q2=0,yf,2=0.40,且F2=4F1。塔顶产品浓度xD=0.93,塔底产品浓度xW=2.6×10-3,塔顶采用全凝器,液体泡点回流,塔釜间接加热,常压操作。试求Rmin。当R=2.0Rmin,写出第二塔段的操作线方程。常压下“丙酮~水”的平衡数据如下:温度液相中丙酮气相中丙酮温度液相中丙酮气相中丙酮
t℃摩尔分率x摩尔分率y t℃摩尔分率x摩尔分率y10092.786.575.866.563.462.161.00.00.010.020.050.100.150.200.300.00.2530.4250.6240.7550.7980.8150.83060.460.059.759.058.257.557.056.130.400.500.600.700.800.900.951.00.8390.8490.8590.8740.8980.9350.9631.0
29)常压下,用一块理论板、全凝器与塔釜组成的连续精馏塔分离某二元混合液。已知:进料xf=0.20,q=1,进料从塔上方加入。塔顶产品浓度xD=0.30,塔顶用全凝器,泡点回流,回流比为3.0。易挥发组分回收率η=0.85,若平衡关系可用表示,试估算A值。
30)以回收塔回收某水溶液中的易挥发组分。α=2.50,进料xf=0.20(摩尔分率,下同),q=1.10,操作中控制塔底排出液浓度xW=0.002。要求馏出液浓度为0.36。试计算所需的理论板数。
第八章塔设备1)拟用清水吸收空气与丙酮混合气中的丙酮。混合气含丙酮4.5%(体积)。操作条件:常压,25℃,塔底液相质量流速GL=6.34kg/(s·m2),液相与气相质量流量之比为2.50,取操作气速为泛点气速的70%。试比较采用25×25×2.5mm瓷质拉西环乱堆与采用25×3.3mm瓷之矩鞍形填料两种方案的空塔气速及每m填料层压降。按塔底条件计算,液相物性按水计。2)承第1题,试计算采用瓷矩鞍形填料时的kGa,该填料的名义尺寸为25mm。
2)计算kL与KLm:计算丙酮在水中的分子扩散系数DL:3)承第1题,试计算采用瓷矩鞍形填料时的kLa,该填料的名义尺寸为25mm。
4)某“乙醇~水”精馏塔,塔顶、底温度分别为78.2℃与102℃,进料中含乙醇16%(摩尔),试查取全塔效率。5)某“苯~甲苯”精馏塔,进料含苯20%(摩尔,下同),塔顶产品含苯98%,塔底产品含苯2.0%,泡点进料,泡点回流,塔顶用全凝器,物系相对挥发度α=2.47。操作回流比为最小回流比的1.5倍。已知气相默弗里单板效率EmV随液相浓度变化不大,可按0.55计。试确定所需实际塔板数及加料板位置。
'
您可能关注的文档
- 化工仪表及自动化习题答案.pdf
- 化工制图习题及答案-高等教育出版社-陆英.doc
- 化工单元操作过程与设备习题答案(上).pdf
- 化工原理下册计算答案.doc
- 化工原理习题答案.pdf
- 化工原理习题解答.doc
- 化工原理书课后习题答案.doc
- 化工原理第二版夏清贾绍义版上册课后习题答案天津大学.pdf
- 化工原理第二版课后习题解答.doc
- 化工原理课后习题解答.doc
- 化工原理课后习题解答1 (1).doc
- 化工热力学(第三版)答案.doc
- 化工热力学第三版(完全版)课后习题答案 (1).doc
- 化工热力学第三版(完全版)课后习题答案.doc
- 化工热力学课后习题答案.doc
- 化工热力学课后作业答案(学生版).doc
- 化工设备机械基础习题和答案.docx
- 化工设备机械基础课后答案.doc