化工原理课后习题解答.doc 73页

'jiujiang化工原理课后习题解答（夏清、陈常贵主编.化工原理.天津大学出版社,2005.）第一章流体流动1.某设备上真空表的读数为13.3×103Pa,试计算设备内的绝对压强与表压强。已知该地区大气压强为98.7×103Pa。解：由绝对压强=大气压强–真空度得到：设备内的绝对压强P绝=98.7×103Pa-13.3×103Pa=8.54×103Pa设备内的表压强P表=-真空度=-13.3×103Pa2．在本题附图所示的储油罐中盛有密度为960㎏/㎥的油品，油面高于罐底6.9m，油面上方为常压。在罐侧壁的下部有一直径为760mm的圆孔，其中心距罐底800mm，孔盖用14mm的钢制螺钉紧固。若螺钉材料的工作应力取为39.23×106Pa，问至少需要几个螺钉？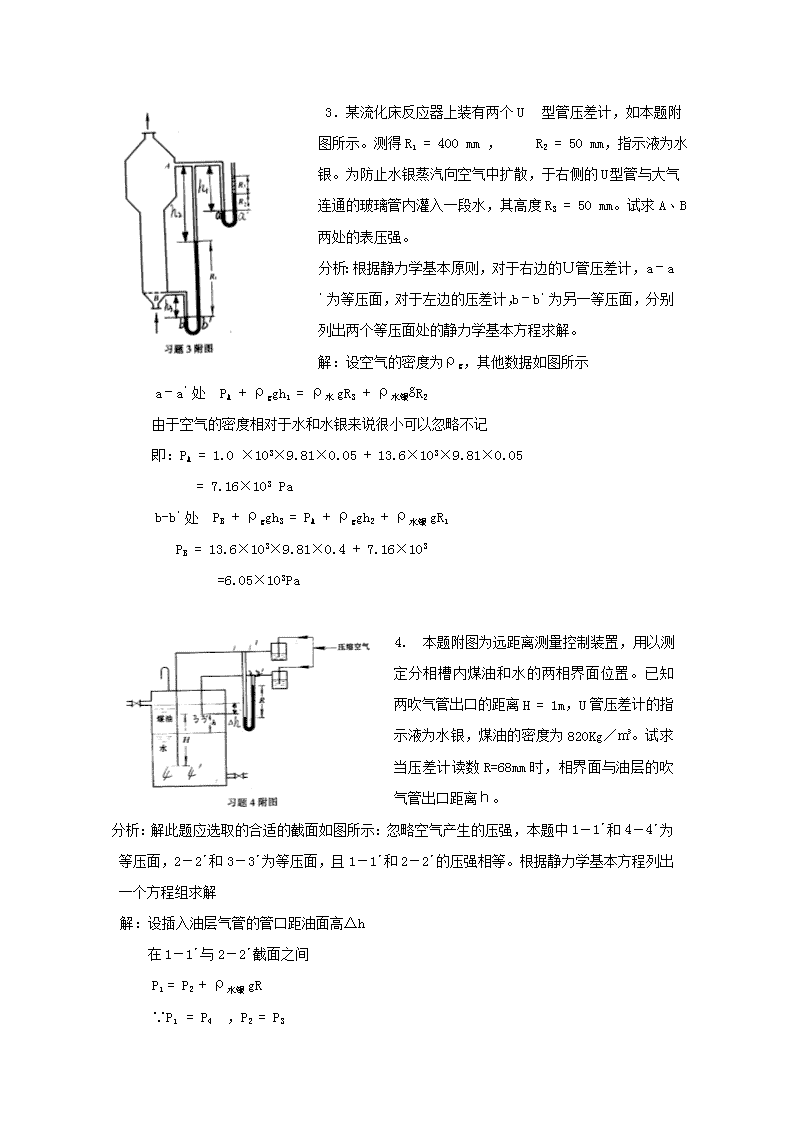分析：罐底产生的压力不能超过螺钉的工作应力即P油≤σ螺解：P螺=ρgh×A=960×9.81×(9.6-0.8)×3.14×0.762150.307×103Nσ螺=39.03×103×3.14×0.0142×nP油≤σ螺得n≥6.23取nmin=7至少需要7个螺钉 3．某流化床反应器上装有两个U型管压差计，如本题附图所示。测得R1=400mm，R2=50mm，指示液为水银。为防止水银蒸汽向空气中扩散，于右侧的U型管与大气连通的玻璃管内灌入一段水，其高度R3=50mm。试求A﹑B两处的表压强。分析：根据静力学基本原则，对于右边的Ｕ管压差计，a–a′为等压面，对于左边的压差计，b–b′为另一等压面，分别列出两个等压面处的静力学基本方程求解。解：设空气的密度为ρg，其他数据如图所示a–a′处PA+ρggh1=ρ水gR3+ρ水银ɡR2由于空气的密度相对于水和水银来说很小可以忽略不记即：PA=1.0×103×9.81×0.05+13.6×103×9.81×0.05=7.16×103Pab-b′处PB+ρggh3=PA+ρggh2+ρ水银gR1PB=13.6×103×9.81×0.4+7.16×103=6.05×103Pa4.本题附图为远距离测量控制装置，用以测定分相槽内煤油和水的两相界面位置。已知两吹气管出口的距离H=1m，U管压差计的指示液为水银，煤油的密度为820Kg／㎥。试求当压差计读数R=68mm时，相界面与油层的吹气管出口距离ｈ。分析：解此题应选取的合适的截面如图所示：忽略空气产生的压强，本题中1－1´和4－4´为等压面，2－2´和3－3´为等压面，且1－1´和2－2´的压强相等。根据静力学基本方程列出一个方程组求解解：设插入油层气管的管口距油面高Δh在1－1´与2－2´截面之间P1=P2+ρ水银gR∵P1=P4，P2=P3 且P3=ρ煤油gΔh，P4=ρ水g（H-h）+ρ煤油g（Δh+h）联立这几个方程得到ρ水银gR=ρ水g（H-h）+ρ煤油g（Δh+h）-ρ煤油gΔh即ρ水银gR=ρ水gH+ρ煤油gh-ρ水gh带入数据1.0³×10³×1-13.6×10³×0.068=h(1.0×10³-0.82×10³)ｈ=0.418ｍ5．用本题附图中串联Ｕ管压差计测量蒸汽锅炉水面上方的蒸气压，Ｕ管压差计的指示液为水银，两Ｕ管间的连接管内充满水。以知水银面与基准面的垂直距离分别为：ｈ1﹦2.3m，ｈ2=1.2m,ｈ3=2.5m,ｈ4=1.4m。锅中水面与基准面之间的垂直距离ｈ5=3m。大气压强ｐa=99.3×103ｐａ。试求锅炉上方水蒸气的压强Ｐ。分析：首先选取合适的截面用以连接两个Ｕ管，本题应选取如图所示的1－1截面，再选取等压面，最后根据静力学基本原理列出方程，求解解：设1－1截面处的压强为Ｐ1对左边的Ｕ管取ａ-ａ等压面，由静力学基本方程Ｐ0+ρ水g(h5-h4)=Ｐ1+ρ水银g(h3-h4)代入数据Ｐ0+1.0×103×9.81×(3-1.4)=Ｐ1+13.6×103×9.81×(2.5-1.4)对右边的Ｕ管取ｂ-ｂ等压面，由静力学基本方程Ｐ1+ρ水g(h3-h2)=ρ水银g(h1-h2)+ｐａ代入数据Ｐ1+1.0×103×9.81×﹙2.5-1.2﹚=13.6×103×9.81×﹙2.3-1.2﹚+99.3×103解着两个方程得Ｐ0=3.64×105Pa6.根据本题附图所示的微差压差计的读数，计算管路中气体的表压强ｐ。压差计中以油和水为指示液，其密度分别为920㎏／ｍ3,998㎏／ｍ3,Ｕ管中油﹑水交接面高度差R= 300ｍｍ，两扩大室的内径D均为60ｍｍ，Ｕ管内径ｄ为6ｍｍ。当管路内气体压强等于大气压时，两扩大室液面平齐。分析：此题的关键是找准等压面，根据扩大室一端与大气相通，另一端与管路相通，可以列出两个方程，联立求解解：由静力学基本原则，选取1－1‘为等压面，对于Ｕ管左边ｐ表+ρ油g(h1+R)=Ｐ1对于Ｕ管右边Ｐ2=ρ水gR+ρ油gh2ｐ表=ρ水gR+ρ油gh2-ρ油g(h1+R)=ρ水gR-ρ油gR+ρ油g（h2-h1）当ｐ表=0时，扩大室液面平齐即π（D/2）2（h2-h1）=π（d/2）2Rh2-h1=3mmｐ表=2.57×102Pa7.列管换热气的管束由121根φ×2.5mm的钢管组成。空气以9m/s速度在列管内流动。空气在管内的平均温度为50℃﹑压强为196×103Pa(表压)，当地大气压为98.7×103Pa试求：⑴空气的质量流量；⑵操作条件下，空气的体积流量；⑶将⑵的计算结果换算成标准状况下空气的体积流量。解：空气的体积流量ＶS=uA=9×π/4×0.022×121=0.342m3/s质量流量ws=ＶSρ=ＶS×(MP)/(RT)=0.342×[29×(98.7+196)]/[8.315×323]=1.09㎏/s换算成标准状况V1P1/V2P2=T1/T2ＶS2=P1T2/P2T1×ＶS1=(294.7×273)/(101×323)×0.342=0.843m3/s8.高位槽内的水面高于地面8m，水从φ108×4mm的管道中流出，管路出口高于地面2m。在本题特定条件下，水流经系统的能量损失可按∑ｈf=6.5u2计算，其中u为水在管道的流速。试计算：⑴A—A"截面处水的流速；⑵水的流量，以m3/h计。 分析：此题涉及的是流体动力学，有关流体动力学主要是能量恒算问题，一般运用的是柏努力方程式。运用柏努力方程式解题的关键是找准截面和基准面，对于本题来说，合适的截面是高位槽1—1,和出管口2—2,,如图所示，选取地面为基准面。解：设水在水管中的流速为u，在如图所示的1—1,，2—2,处列柏努力方程Z1ｇ+0+Ｐ1/ρ=Z2ｇ+ｕ2／2+Ｐ2/ρ+∑ｈf（Z1-Z2）g=u2/2+6.5u2代入数据(8-2)×9.81=7u2,u=2.9m/s换算成体积流量VS=uA=2.9×π/4×0.12×3600=82m3/h9.20℃水以2.5m/s的流速流经φ38×2.5mm的水平管，此管以锥形管和另一φ53×3m的水平管相连。如本题附图所示，在锥形管两侧A、B处各插入一垂直玻璃管以观察两截面的压强。若水流经A﹑B两截面的能量损失为1.5J/㎏，求两玻璃管的水面差（以ｍｍ计），并在本题附图中画出两玻璃管中水面的相对位置。分析:根据水流过A、B两截面的体积流量相同和此两截面处的伯努利方程列等式求解解：设水流经Ａ﹑Ｂ两截面处的流速分别为uA、uBuAAA=uBAB∴uB=（AA/AB）uA=（33/47）2×2.5=1.23m/s在Ａ﹑Ｂ两截面处列柏努力方程Z1ｇ+ｕ12／2+Ｐ1/ρ=Z2ｇ+ｕ22／2+Ｐ2/ρ+∑ｈf∵Z1=Z2∴（Ｐ1-Ｐ2）/ρ=∑ｈf+（ｕ12-ｕ22）／2g（h1-h2）=1.5+(1.232-2.52)/2h1-h2=0.0882m=88.2mm即两玻璃管的水面差为88.2mm 10.用离心泵把20℃的水从贮槽送至水洗塔顶部，槽内水位维持恒定，各部分相对位置如本题附图所示。管路的直径均为Ф76×2.5mm，在操作条件下，泵入口处真空表的读数为24.66×10³Pa,水流经吸入管与排处管（不包括喷头）的能量损失可分别按∑ｈf,1=2u²，∑hf,2=10u2计算，由于管径不变，故式中u为吸入或排出管的流速ｍ/s。排水管与喷头连接处的压强为98.07×10³Pa（表压）。试求泵的有效功率。分析：此题考察的是运用柏努力方程求算管路系统所要求的有效功率把整个系统分成两部分来处理，从槽面到真空表段的吸入管和从真空表到排出口段的排出管，在两段分别列柏努力方程。解：总能量损失∑hf=∑hf+，1∑hf，2u1=u2=u=2u2+10u²=12u²在截面与真空表处取截面作方程：z0g+u02/2+P0/ρ=z1g+u2/2+P1/ρ+∑hf，1（P0-P1）/ρ=z1g+u2/2+∑hf，1∴u=2m/s∴ws=uAρ=7.9kg/s在真空表与排水管-喷头连接处取截面z1g+u2/2+P1/ρ+We=z2g+u2/2+P2/ρ+∑hf，2∴We=z2g+u2/2+P2/ρ+∑hf，2—（z1g+u2/2+P1/ρ）=12.5×9.81+（98.07+24.66）/998.2×10³+10×2²=285.97J/kgNe=Wews=285.97×7.9=2.26kw11.本题附图所示的贮槽内径D为2ｍ，槽底与内径d0为33mm的钢管相连，槽内无液体补充，其液面高度h0为2m（以管子中心线为基准）。液体在本题管内流动时的全部能量损失可按∑hf=20u²公式来计算，式中u为液体在管内的流速m／s。试求当槽内液面下降1m所需的时间。分析：此题看似一个普通的解柏努力方程的题，分析题中槽内无液体补充，则管内流速并不是一个定值而是一个关于液面高度的函数，抓住槽内和管内的体积流量相等列出一个微分方程，积分求解。 解：在槽面处和出口管处取截面1-1，2-2列柏努力方程h1g=u2/2+∑hf=u2/2+20u2∴u=(0.48h)1/2=0.7h1/2槽面下降dh，管内流出uA2dt的液体∴Adh=uA2dt=0.7h1/2A2dt∴dt=A1dh/（A20.7h1/2）对上式积分：t=1.⒏h12.本题附图所示为冷冻盐水循环系统，盐水的密度为1100kg／m³，循环量为36m³。管路的直径相同，盐水由A流经两个换热器而至B的能量损失为98.1J／kg，由B流至A的能量损失为49J／kg，试求：（1）若泵的效率为70%时，泵的抽功率为若干kw？（2）若A处的压强表读数为245.2×10³Pa时，B处的压强表读数为若干Pa？分析：本题是一个循环系统，盐水由A经两个换热器被冷却后又回到A继续被冷却，很明显可以在A-换热器-B和B-A两段列柏努利方程求解。解：（1）由A到B截面处作柏努利方程0+uA²/2+PA/ρ1=ZBg+uB²／2+PB／ρ+9.81管径相同得uA=uB∴（PA-PB）/ρ=ZBg+9.81由B到A段，在截面处作柏努力方程BZBg+uB²／2+PB/ρ+We=0+uA²+PA/ρ+49∴We=（PA-PB）/ρ-ZBg+49=98.1+49=147.1J/kg∴WS=VSρ=36/3600×1100=11kg/sNe=We×WS=147.1×11=1618.1w泵的抽功率N=Ne/76%=2311.57W=2.31kw（2）由第一个方程得（PA-PB）/ρ=ZBg+9.81得PB=PA-ρ（ZBg+9.81）=245.2×10³-1100×(7×9.81+98.1)=6.2×104Pa 13.用压缩空气将密度为1100kg/m3的腐蚀性液体自低位槽送到高位槽，两槽的液位恒定。管路直径均为ф60×3.5mm，其他尺寸见本题附图。各管段的能量损失为∑ｈf，AB=∑ｈf，CD=u2，∑ｈf，BC=1.18u2。两压差计中的指示液均为水银。试求当R1=45mm，h=200mm时：（1）压缩空气的压强P1为若干？（2）U管差压计读数R2为多少？解：对上下两槽取截面列柏努力方程0+0+P1/ρ=Zg+0+P2/ρ+∑ｈf∴P1=Zgρ+0+P2+ρ∑ｈf=10×9.81×1100+1100（2u2+1.18u2）=107.91×10³+3498u²在压强管的B，C处去取截面，由流体静力学方程得PB+ρg（x+R1）=Pc+ρg（hBC+x）+ρ水银R1gPB+1100×9.81×（0.045+x）=Pc+1100×9.81×（5+x）+13.6×10³×9.81×0.045PB-PC=5.95×104Pa在B，C处取截面列柏努力方程0+uB²/2+PB/ρ=Zg+uc2/2+PC/ρ+∑ｈf，BC∵管径不变，∴ub=ucPB-PC=ρ（Zg+∑ｈf，BC）=1100×（1.18u2+5×9.81）=5.95×104Pau=4.27m/s压缩槽内表压P1=1.23×105Pa（2）在B，D处取截面作柏努力方程0+u2/2+PB/ρ=Zg+0+0+∑ｈf，BC+∑ｈf，CDPB=（7×9.81+1.18u2+u2-0.5u2）×1100=8.35×104PaPB-ρgh=ρ水银R2g8.35×104-1100×9.81×0.2=13.6×10³×9.81×R2R2=609.7mm14.在实验室中,用玻璃管输送20℃的70%醋酸.管内径为1.5cm,流量为10kg/min,用SI和物理单位各算一次雷诺准数,并指出流型。 解：查20℃，70％的醋酸的密度ρ=1049Kg/m3,粘度µ=2.6mPa·s用SI单位计算：d=1.5×10-2m,u=WS/(ρA)=0.9m/s∴Re=duρ/μ=(1.5×10-2×0.9×1049)/(2.6×103)=5.45×103用物理单位计算：ρ=1.049g/cm³,u=WS/(ρA)=90cm/s,d=1.5cmμ=2.6×10-3Pa•S=2.6×10-3kg/(s•m)=2.6×10-2g/s•cm-1∴Re=duρ/μ=(1.5×90×1.049)/(2.6×10-2)=5.45×103∵5.45×103>4000∴此流体属于湍流型15.在本题附图所示的实验装置中，于异径水平管段两截面间连一倒置U管压差计，以测量两截面的压强差。当水的流量为10800kg/h时，U管压差计读数R为100mm，粗细管的直径分别为Ф60×3.5mm与Ф45×3.5mm。计算：（1）1kg水流经两截面间的能量损失。（2）与该能量损失相当的压强降为若干Pa？解：（1）先计算A，B两处的流速：uA=ws/ρsA=295m/s，uB=ws/ρsB在A，B截面处作柏努力方程：zAg+uA2/2+PA/ρ=zBg+uB2/2+PB/ρ+∑hf∴1kg水流经A，B的能量损失：∑hf=（uA2-uB2）/2+（PA-PB）/ρ=（uA2-uB2）/2+ρgR/ρ=4.41J/kg（2）.压强降与能量损失之间满足：∑hf=ΔP/ρ∴ΔP=ρ∑hf=4.41×10³16.密度为850kg/m³，粘度为8×10-3Pa·s的液体在内径为14mm的钢管内流动，溶液的流速为1m/s。试计算：（1）泪诺准数，并指出属于何种流型？（2）局部速度等于平均速度处与管轴的距离；（3）该管路为水平管，若上游压强为147×10³Pa，液体流经多长的管子其压强才下降到127.5×10³Pa？ 解：（1）Re=duρ/μ=（14×10-3×1×850）/（8×10-3）=1.49×10³>2000∴此流体属于滞流型（2）由于滞流行流体流速沿管径按抛物线分布，令管径和流速满足y2=-2p（u-um）当ｕ=0时,y2=r2=2pum∴p=r2/2=d2/8当ｕ=ｕ平均=0.5ｕmax=0.5m/s时,y2=-2p（0.5-1）=d2/8=0.125d2∴即与管轴的距离r=4.95×10-3m(3)在147×103和127.5×103两压强面处列伯努利方程u12/2+PA/ρ+Z1g=u22/2+PB/ρ+Z2g+∑ｈf∵u1=u2,Z1=Z2∴PA/ρ=PB/ρ+∑ｈf损失能量ｈf=（PA-PB）/ρ=（147×103-127.5×103）/850=22.94∵流体属于滞流型∴摩擦系数与雷若准数之间满足λ=64/Re又∵ｈf=λ×（ι/d）×0.5u2∴ι=14.95m∵输送管为水平管，∴管长即为管子的当量长度即：管长为14.95m17.流体通过圆管湍流动时，管截面的速度分布可按下面经验公式来表示：ur=umax（y/R）1/7，式中y为某点与壁面的距离，及y=R—r。试求起平均速度u与最大速度umax的比值。分析：平均速度u为总流量与截面积的商，而总流量又可以看作是速度是ur的流体流过2πrdr的面积的叠加即：V=∫0Rur×2πrdr解：平均速度u=V/A=∫0Rur×2πrdr/（πR2）=∫0Rumax（y/R）1/7×2πrdr/（πR2） =2umax/R15/7∫0R（R–r）1/7rdr=0.82umaxu/umax=0.8218.一定量的液体在圆形直管内做滞流流动。若管长及液体物性不变，而管径减至原有的1/2，问因流动阻力而产生的能量损失为原来的若干倍？解：∵管径减少后流量不变∴u1A1=u2A2而r1=r2∴A1=4A2∴u2=4u由能量损失计算公式∑ｈf=λ•（ι/d）×（1/2u2）得∑ｈf，1=λ•（ι/d）×（1/2u12）∑ｈf，2=λ•（ι/d）×（1/2u22）=λ•（ι/d）×8（u1）2=16∑ｈf，1∴hf2=16hf119.内截面为1000mm×1200mm的矩形烟囱的高度为30A1m。平均分子量为30kg/kmol，平均温度为400℃的烟道气自下而上流动。烟囱下端维持49Pa的真空度。在烟囱高度范围内大气的密度可视为定值，大气温度为20℃，地面处的大气压强为101.33×10³Pa。流体经烟囱时的摩擦系数可取为0.05，试求烟道气的流量为若干kg/h？解：烟囱的水力半径rН=A/п=(1×1.2)/2(1+1.2)=0.273m当量直径de=4rН=1.109m流体流经烟囱损失的能量∑ｈf=λ•（ι/de）·u2/2=0.05×(30/1.109)×u2/2=0.687u2空气的密度ρ空气=PM/RT=1.21Kg/m3烟囱的上表面压强(表压)P上=-ρ空气gh=1.21×9.81×30=-355.02Pa烟囱的下表面压强(表压)P下=-49Pa烟囱内的平均压强P=(P上+P下)/2+P0=101128Pa 由ρ=PM/RT可以得到烟囱气体的密度ρ=（30×10-3×101128）/（8.314×673）=0.5422Kg/m3在烟囱上下表面列伯努利方程P上/ρ=P下/ρ+Zg+∑ｈf∴∑ｈf=(P上-P下)/ρ–Zg=(-49+355.02)/0.5422–30×9.81=268.25=0.687u2流体流速u=19.76m/s质量流量ωs=uAρ=19.76×1×1.2×0.5422=4.63×104Kg/h20.每小时将2×10³kg的溶液用泵从反应器输送到高位槽。反应器液面上方保持26.7×10³Pa的真空读，高位槽液面上方为大气压强。管道为的钢管，总长为50m，管线上有两个全开的闸阀，一个孔板流量计（局部阻力系数为4），5个标准弯头。反应器内液面与管路出口的距离为15m。若泵效率为0.7，求泵的轴功率。解：流体的质量流速ωs=2×104/3600=5.56kg/s流速u=ωs/(Aρ)=1.43m/s雷偌准数Re=duρ/μ=165199>4000查本书附图1-29得5个标准弯头的当量长度:5×2.1=10.5m2个全开阀的当量长度:2×0.45=0.9m∴局部阻力当量长度∑ιe=10.5+0.9=11.4m假定1/λ1/2=2lg(d/ε)+1.14=2lg(68/0.3)+1.14∴λ=0.029检验d/(ε×Re×λ1/2)=0.008>0.005∴符合假定即λ=0.029∴全流程阻力损失∑ｈ=λ×(ι+∑ιe)/d×u2/2+ζ×u2/2=[0.029×(50+11.4)/(68×103)+4]×1.432/2 =30.863J/Kg在反应槽和高位槽液面列伯努利方程得P1/ρ+We=Zg+P2/ρ+∑ｈWe=Zg+(P1-P2)/ρ+∑ｈ=15×9.81+26.7×103/1073+30.863=202.9J/Kg有效功率Ne=We×ωs=202.9×5.56=1.128×103轴功率N=Ne/η=1.128×103/0.7=1.61×103W=1.61KW21.从设备送出的废气中有少量可溶物质，在放空之前令其通过一个洗涤器，以回收这些物质进行综合利用，并避免环境污染。气体流量为3600m³/h，其物理性质与50℃的空气基本相同。如本题附图所示，气体进入鼓风机前的管路上安装有指示液为水的U管压差计，起读数为30mm。输气管与放空管的内径均为250mm，管长与管件，阀门的当量长度之和为50m，放空机与鼓风机进口的垂直距离为20m，已估计气体通过塔内填料层的压强降为1.96×10³Pa。管壁的绝对粗糙度可取0.15mm，大气压强为101.33×10³。求鼓风机的有效功率。解：查表得该气体的有关物性常数ρ=1.093,μ=1.96×10-5Pa·s气体流速u=3600/(3600×4/π×0.252)=20.38m/s质量流量ωs=uAs=20.38×4/π×0.252×1.093=1.093Kg/s流体流动的雷偌准数Re=duρ/μ=2.84×105为湍流型所有当量长度之和ι总=ι+Σιe=50mε取0.15时ε/d=0.15/250=0.0006查表得λ=0.0189所有能量损失包括出口,入口和管道能量损失即:∑ｈ=0.5×u2/2+1×u2/2+(0.0189×50/0.25)·u2/2 =1100.66在1-1﹑2-2两截面处列伯努利方程u2/2+P1/ρ+We=Zg+u2/2+P2/ρ+∑ｈWe=Zg+(P2-P1)/ρ+∑ｈ而1-1﹑2-2两截面处的压强差P2-P1=P2-ρ水gh=1.96×103-103×9.81×31×103=1665.7Pa∴We=2820.83W/Kg泵的有效功率Ne=We×ωs=3083.2W=3.08KW22.如本题附图所示，，贮水槽水位维持不变。槽底与内径为100mm的钢质放水管相连，管路上装有一个闸阀，距管路入口端15m处安有以水银为指示液的U管差压计，其一臂与管道相连，另一臂通大气。压差计连接管内充满了水，测压点与管路出口端之间的长度为20m。（1）.当闸阀关闭时，测得R=600mm，h=1500mm；当闸阀部分开启时，测的R=400mm，h=1400mm。摩擦系数可取0.025，管路入口处的局部阻力系数为0.5。问每小时从管中水流出若干立方米。（2）.当闸阀全开时，U管压差计测压处的静压强为若干（Pa，表压）。闸阀全开时le/d≈15，摩擦系数仍取0.025。解:⑴根据流体静力学基本方程,设槽面到管道的高度为xρ水g(h+x)=ρ水银gR103×(1.5+x)=13.6×103×0.6x=6.6m部分开启时截面处的压强P1=ρ水银gR-ρ水gh=39.63×103Pa在槽面处和1-1截面处列伯努利方程Zg+0+0=0+u2/2+P1/ρ+∑ｈ而∑ｈ=［λ(ι+Σιe)/d+ζ］·u2/2 =2.125u2∴6.6×9.81=u2/2+39.63+2.125u2u=3.09/s体积流量ωs=uAρ=3.09×π/4×(0.1)2×3600=87.41m3/h⑵闸阀全开时取2-2,3-3截面列伯努利方程Zg=u2/2+0.5u2/2+0.025×(15+ι/d)u2/2u=3.47m/s取1-1﹑3-3截面列伯努利方程P1"/ρ=u2/2+0.025×(15+ι"/d)u2/2∴P1"=3.7×104Pa23.10℃的水以500L/min的流量流过一根长为300m的水平管，管壁的绝对粗糙度为0.05。有6m的压头可供克服流动阻力，试求管径的最小尺寸。解:查表得10℃时的水的密度ρ=999.7Kg/m3µ=130.77×10-5Pa·su=Vs/A=10.85×10-3/d2∵∑ｈf=6×9.81=58.86J/Kg∑ｈf=(λ·ι/d)u2/2=λ·150u2/d假设为滞流λ=64/Re=64μ/duρ∵Hfg≥∑ｈf∴d≤1.5×10-3检验得Re=7051.22>2000∴不符合假设∴为湍流假设Re=9.7×104即duρ/μ=9.7×104∴d=8.34×10-2m则ε/d=0.0006查表得λ=0.021要使∑ｈf≤Hfg成立则λ·150u2/d≤58.86d≥1.82×10-2m 24.某油品的密度为800kg/m³，粘度为41cP，由附图所示的A槽送至B槽，A槽的液面比B槽的液面高出1.5m。输送管径为ф89×3.5mm（包括阀门当量长度），进出口损失可忽略。试求：（1）油的流量（m³/h）；（2）若调节阀门的开度，使油的流量减少20%，此时阀门的当量长度为若干m？解：⑴在两槽面处取截面列伯努利方程u2/2+Zg+P1/ρ=u2/2+P2/ρ+∑ｈf∵P1=P2Zg=∑ｈf=λ·(ι/d)·u2/21.5×9.81=λ•(50/82×10-3)·u2/2①假设流体流动为滞流,则摩擦阻力系数λ=64/Re=64μ/duρ②联立①②两式得到u=1.2m/s核算Re=duρ/μ=1920<2000假设成立油的体积流量ωs=uA=1.2×π/4(82×103)2×3600=22.8m3/h⑵调节阀门后的体积流量ωs"=22.8×(1-20％)=18.24m3/h调节阀门后的速度u=0.96m/s同理由上述两式1.5×9.81=λ•(ι/82×10-3)·0.962/2λ=64/Re=64μ/duρ可以得到ι=62.8m∴阀门的当量长度ιe=ι-50=12.8m25.在两座尺寸相同的吸收塔内，各填充不同的填料，并以相同的管路并联组合。每条支管上均装有闸阀，两支路的管长均为5m（均包括除了闸阀以外的管件局部阻力的当量长度），管内径为200mm。通过田料层的能量损失可分别折算为5u1²与4u2²，式中u为气体在管内的流速m/s，气体在支管内流动的摩擦系数为0.02。管路的气体总流量为0.3m³/s。试求：（1）两阀全开时，两塔的通气量；（2）附图中AB的能量损失。分析：并联两管路的能量损失相等，且各等于管路总的能量损失,各个管路的能量损失由两部分组成，一是气体在支管内流动产生的，而另一部分是气体通过填料层所产生的，即∑ｈf=λ·(ι＋∑ιe/d)·u2/2　＋ｈf填而且并联管路气体总流量为个支路之和,即Vs=Vs1 +Vs2解：⑴两阀全开时，两塔的通气量由本书附图１－２９查得d=200mm时阀线的当量长度ιe=150m∑ｈf1=λ·(ι1＋∑ιe1/d)·u12/2+5u12=0.02×(50+150)/0.2·u12/2+5u12∑ｈf2=λ·(ι2＋∑ιe2/d)·u22/2+4u12=0.02×(50+150)/0.2·u22/2+4u12∵∑ｈf1=∑ｈf2∴u12/u22=11.75/12.75即u1=0.96u2又∵Vs=Vs1+Vs2=u1A1+u2A2,A1=A2=(0.2)2π/4=0.01π=(0.96u2+u2)•0.01π=0.3∴u2=4.875m/su1A=4.68m/s即两塔的通气量分别为Vs1=0.147m3/s,Vs12=0.153m3/s⑵总的能量损失∑ｈf=∑ｈf1=∑ｈf2=0.02×155/0.2·u12/2+5u12=12.5u12=279.25J/Kg26.用离心泵将20℃水经总管分别送至A，B容器内，总管流量为89m/h³，总管直径为ф127×5mm。原出口压强为1.93×105Pa，容器B内水面上方表压为1kgf/cm²，总管的流动阻力可忽略，各设备间的相对位置如本题附图所示。试求：（1）离心泵的有效压头He；（2）两支管的压头损失Hf，o-A，Hf，o-B，。解：（1）离心泵的有效压头总管流速u=Vs/A而A=3600×π/4×(117)2×10-6 u=2.3m/s在原水槽处与压强计管口处去截面列伯努利方程Z0g+We=u2/2+P0/ρ+∑ｈf∵总管流动阻力不计∑ｈf=0We=u2/2+P0/ρ-Z0g=2.32/2+1.93×105/998.2-2×9.81=176.38J/Kg∴有效压头He=We/g=17.98m⑵两支管的压头损失在贮水槽和Α﹑Β表面分别列伯努利方程Z0g+We=Z1g+P1/ρ+∑ｈf1Z0g+We=Z2g+P2/ρ+∑ｈf2得到两支管的能量损失分别为∑ｈf1=Z0g+We–(Z1g+P1/ρ)=2×9.81+176.38–(16×9.81+0)=39.04J/Kg∑ｈf2=Z0g+We-(Z2g+P2/ρ)=2×9.81+176.38–(8×9.81+101.33×103/998.2)=16.0J/Kg∴压头损失Hf1=∑ｈf1/g=3.98mHf2=∑ｈf2/g=1.63m27.用效率为80%的齿轮泵将粘稠的液体从敞口槽送至密闭容器中，两者液面均维持恒定，容器顶部压强表读数为30×103Pa。用旁路调节流量，起流程如本题附图所示，主管流量为14m3/h，管径为φ66×3mm，管长为80m（包括所有局部阻力的当量长度）。旁路的流量为5m3/h，管径为Φ32×2.5mm，管长为20m（包括除阀门外的管件局部阻力的当量长度）两管路的流型相同，忽略贮槽液面至分支点o之间的能量损失。被输送液体的粘度为50mPa·s，密度为1100kg/m³，试计算：（1）泵的轴功率（2）旁路阀门的阻力系数。解：⑴泵的轴功率 分别把主管和旁管的体积流量换算成流速主管流速u=V/A=14/[3600×(π/4)×(60)2×10-6]=1.38m/s旁管流速u1=V1/A=5/[3600×(π/4)×(27)2×10-6]=2.43m/s先计算主管流体的雷偌准数Re=duρ/μ=1821.6<2000属于滞流摩擦阻力系数可以按下式计算λ=64/Re=0.03513在槽面和容器液面处列伯努利方程We=Z2g+P2/ρ+∑ｈf=5×9.81+30×103/1100+0.03513×1.382×80/(60×10-3)=120.93J/Kg主管质量流量ωs=uAρ=1.38×(π/4)×(60)2×1100=5.81Kg/s泵的轴功率Ne/η=We×ωs/η=877.58W=0.877KW⑵旁路阀门的阻力系数旁管也为滞流其摩擦阻力系数λ1=64/Re1=0.04434有效功We=0+u12/2+0+∑ｈf=u12/2+λ·u12/2·20/d1+ε•u12/2∴旁路阀门的阻力系数ε=(We-u12/2-λ·u12/2·20/d1)-2/u12=7.1128．本题附图所示为一输水系统，高位槽的水面维持恒定，水分别从BC与BD两支管排出，高位槽液面与两支管出口间的距离为11m，AB段内径为38mm，长为58m；BC支管内径为32mm，长为12.5m；BD支管的内径为26mm，长为14m，各段管长均包括管件及阀门全开时的当量长度。AB与BC管的摩擦系数为0.03。试计算： (1)当BD支管的阀门关闭时，BC支管的最大排水量为若干m³/h？(2)当所有的阀门全开时，两支管的排水量各为若干m³/h？BD支管的管壁绝对粗糙度为0.15mm，水的密度为1000kg/m³，粘度为0.001Pa·s。分析：当BD支管的阀门关闭时，BC管的流量就是AB总管的流量；当所有的阀门全开时，AB总管的流量应为BC，BD两管流量之和。而在高位槽内，水流速度可以认为忽略不计。解:（1）BD支管的阀门关闭VS,AB=VS,BC即u0A0=u1A1u0π382/4=u1π322/4∴u0=0.71u1分别在槽面与C-C,B-B截面处列出伯努利方程0+0+Z0g=u12/2+0+0+∑ｈf,AC0+0+Z1g=u02/2+0+0+∑ｈf,AB而∑ｈf,AC=λ•(ιAB/d0)·u02/2+λ•(ιBC/d1)·u12/2=O.03×(58000/38)×u02/2+0.03·(12500/32)×u12/2=22.89u02+5.86u12∑ｈf,AB=λ•(ιAB/d0)·u02/2=O.03×(58000/38)×u02/2=22.89u02∴u1=2.46m/sBC支管的排水量VS,BC=u1A1=7.1m3/s⑵所有的阀门全开VS,AB=VS,BC+VS,BDu0A0=u1A1+u2A2u0π382/4=u1π322/4+u2π262/4u0382=u1322+u2262①假设在BD段满足1/λ1/2=2lg(d/ε)+1.14∴λD=0.0317同理在槽面与C-C,D-D截面处列出伯努利方程Z0g=u12/2+∑ｈf,AC=u12/2+λ•(ιAB/d0)·u02/2+λ•(ιBC/d1)·u12/2②Z0g=u22/2+∑ｈf,AD =u22/2+λ•(ιAB/d0)·u02/2+λD•(ιBD/d2)·u22/2③联立①②③求解得到u1=1.776m/s,u2=1.49m/s核算Re=duρ/μ=26×10-3×1.49×103/0.001=38.74×103(d/ε)/Reλ1/2=0.025>0.005∴假设成立即D,C两点的流速u1=1.776m/s,u2=1.49m/s∴BC段和BD的流量分别为VS,BC=32×10×(π/4)×3600×1.776=5.14m3/sVS,BD=26×10×(π/4)×3600×1.49=2.58m3/s29.在Φ38×2.5mm的管路上装有标准孔板流量计，孔板的孔径为16.4mm，管中流动的是20℃的苯，采用角接取压法用U管压差计测量孔板两测的压强差，以水银为指示液，策压连接管中充满甲苯。测得U管压差计的读数为600mm，试计算管中甲苯的流量为若干kg/h？解：查本书附表20℃时甲苯的密度和粘度分别为ρ=867Kg/m3,μ=0.675×10-3假设Re=8.67×104当A0/A1=(16.4/33)=0.245时,查孔板流量计的C0与Re,A0/A1的关系得到C0=0.63体积流量VS=C0A0[2gR(ρA-ρ)/ρ]1/2=0.63×π/4×16.42×10-6×[2×9.81×0.6×(13.6-0.867)/0.867]1/2=1.75×10-3m3/s流速u=VS/A=2.05m/s核算雷偌准数Re=duρ/μ=8.67×104与假设基本相符∴甲苯的质量流量ωS=VSρ=1.75×10-3×867×3600=5426Kg/h第二章流体输送机械 1.在用水测定离心泵性能的实验中，当流量为26m³/h时，泵出口处压强表和入口处真空表的读数分别为152kPa和24.7kPa，轴功率为2.45kw，转速为2900r/min，若真空表和压强表两测压口间的垂直距离为0.4m，泵的进出口管径相同，两测压口间管路流动阻力可忽略不计，试求该泵的效率，并列出该效率下泵的性能。解：取20℃时水的密度ρ=998.2Kg/m3在泵出口和入口处列伯努利方程u12/2g+P1/ρg+Η=u12/2g+P2/ρg+Ηf+Z∵泵进出口管径相同,u1=u2不计两测压口见管路流动阻力Ηf=0∴P1/ρg+Η=P2/ρg+ZΗ=(P2-P1)/ρg+Z=0.4+(152+24.7)×103/998.2×9.8=18.46m该泵的效率η=QHρg/N=26×18.46×998.2×9.8/(2.45×103×3600)=53.2.﹪2.用离心泵以40m³/h的流量将贮水池中65℃的热水输送到凉水塔顶，并经喷头喷出而落入凉水池中，以达到冷却的目的，已知水进入喷头之前需要维持49kPa的表压强，喷头入口较贮水池水面高6m，吸入管路和排出管路中压头损失分别为1m和3m，管路中的动压头可以忽略不计。试选用合适的离心泵并确定泵的安装高度。当地大气压按101.33kPa计。解：∵输送的是清水∴选用B型泵查65℃时水的密度ρ=980.5Kg/m3在水池面和喷头处列伯努利方程u12/2g+P1/ρg+Η=u12/2g+P2/ρg+Ηf+Z取u1=u2=0则Η=(P2-P1)/ρg+Ηf+Z=49×103/980.5×9.8+6+(1+4)=15.1m∵Q=40m3/h由图2-27得可以选用3B19A2900465℃时清水的饱和蒸汽压PV=2.544×104Pa 当地大气压Ηa=P/ρg=101.33×103/998.2×9.81=10.35m查附表二十三3B19A的泵的流量:29.5—48.6m3/h为保证离心泵能正常运转,选用最大输出量所对应的ΗS"即ΗS"=4.5m输送65℃水的真空度ΗS=[ΗS"+(Ηa-10)-(PV/9.81×103–0.24)]1000/ρ=2.5m∴允许吸上高度Hg=ΗS-u12/2g-Ηf,0-1=2.5–1=1.5m即安装高度应低于1.5m3．常压贮槽内盛有石油产品，其密度为760kg/m³，粘度小于20cSt，在贮槽条件下饱和蒸汽压为80kPa，现拟用65Y-60B型油泵将此油品以15m³流量送往表压强为177kPa的设备内。贮槽液面恒定，设备的油品入口比贮槽液面高5m，吸入管路和排出管路的全部压头损失为1m和4m。试核算该泵是否合用。若油泵位于贮槽液面以下1.2m处，问此泵能否正常操作？当地大气压按101.33kPa计.解:查附录二十三65Y-60B型泵的特性参数如下流量Q=19.8m3/s,气蚀余量△h=2.6m扬程H=38m允许吸上高度Hg=(P0-PV)/ρg-△h-Ηf,0-1=-0.74m>-1.2扬升高度Z=H-Ηf,0-2=38–4=34m如图在1-1,2-2截面之间列方程u12/2g+P1/ρg+Η=u22/2g+P2/ρg+Ηf,1-2+△Z其中u12/2g=u22/2g=0管路所需要的压头:Ηe=(P2–P1)/ρg+△Z+Ηf,1-2=33.74m2×105∴假设成立u1=u2(d2/d1)2=1.23m/s允许气蚀余量△h=(P1-P2)/ρg+u12/2gP1=Pa-P真空度=28.02Kpa△h=(28.02-2.3346)×103/998.2×9.81=2.7m允许吸上高度Hg=(Pa-PV)/ρg-△h-∑Ηf∵离心泵离槽面道路很短可以看作∑Ηf=0∴Hg=(Pa-PV)/ρg-△h=(101.4–2.3346)×103/(998.2×9.81)–2.7=7.42m5.水对某离心泵做实验，得到下列各实验数据：Q，L/min0100200300400500 H，m37.2383734.531.828.5送液体的管路系统：管径为ф76×4mm，长为355m（包括局部阻力的当量长度），吸入和排出空间为密闭容器，其内压强为129.5kPa（表压），再求此时泵的流量。被输送液体的性质与水相近。解:⑴根据管路所需要压头Ηe与液体流量Qe的关系:Ηe=K+BQe2而K=△Z+△P/ρg且吸入排出空间为常压设备,△P=0∴K=△Z=4.8B=λ•(ι+Σιe)/d·1/2g(60×103A)2=(0.03×355/0.068)/2×9.81(0.0682×π×60×103/4)2=1.683×10-4∴管道特性方程为:Ηe=4.8+1.683×10-4Qe2由下列数据绘出管道特性曲线Ηe--QeQe,L/min0100200300400500Ηe,m4.86.4811.5319.9531.7346.88绘出离心泵的特性曲线H--Q于同一坐标系中,如图所示:两曲线的交点即为该泵在运转时的流量∴泵的流量为400L/min⑵若排出空间为密闭容器,则K=△Z+△P/ρg=4.8+129.5×103/998.2×9.81=1.802∵而B的值保持不变∴管路的特性方程为Ηe=18.02+1.683×10-4Qe2重新绘出管路的特性曲线和泵的特性曲线Qe,L/min0100200300400500Ηe,m18.0219.7024.7533.1744.9560.10可以得到泵的流量为310L/min 6.某型号的离心泵，其压头与流量的关系可表示为H=18-0.6×106Q2（H单位为m，Q单位为m³/s）若用该泵从常压贮水池将水抽到渠道中，已知贮水池截面积为100m²，池中水深7m。输水之初池内水面低于渠道水平面2m，假设输水渠道水面保持不变，且与大气相通。管路系统的压头损失为Hf=0.4×10Q2（Hf单位为m，Q单位为m³/s）。试求将贮水池内水全部抽出所需时间。解:列出管路特性方程Ηe=K+HfK=△Z+△P/ρg∵贮水池和渠道均保持常压∴△P/ρg=0∴K=△Z∴Ηe=△Z+0.4×106Q2在输水之初△Z=2m∴Ηe=2+0.4×106Q2联立H=18-0.6×106Q2，解出此时的流量Q=4×10-3m3/s将贮水槽的水全部抽出△Z=9m∴Ηe=9+0.4×106Q"2再次联立H=18-0.6×106Q2，解出此时的流量Q"=3×10-3m3/s∵流量Q随着水的不断抽出而不断变小∴取Q的平均值Q平均=（Q+Q"）/2=3.5×10-3m3/s把水抽完所需时间τ=V/Q平均=55.6h7.用两台离心泵从水池向高位槽送水，单台泵的特性曲线方程为H=25—1×106Q²管路特性曲线方程可近似表示为H=10+1×106Q²两式中Q的单位为m³/s，H的单位为m。试问两泵如何组合才能使输液量最大？（输水过程为定态流动）分析：两台泵有串联和并联两种组合方法串联时单台泵的送水量即为管路中的总量，泵的压头为单台泵的两倍；并联时泵的压头即为单台泵的压头，单台送水量为管路总送水量的一半解：①串联He=2H10+1×105Qe2=2×(25-1×106Q2)∴Qe=0.436×10-2m2/s ②并联Q=Qe/225-1×106×Qe2=10+1×105(Qe/2)2∴Qe=0.383×10-2m2/s总送水量Qe"=2Qe=0.765×10-2m2/s∴并联组合输送量大8.现采用一台三效单动往复泵，将敞口贮罐中密度为1250kg/m³的液体输送到表压强为1.28×106Pa的塔内，贮罐液面比塔入口低10m，管路系统的总压头损失为2m，已知泵活塞直径为70mm，冲程为225mm，往复次数为2001/min，泵的总效率和容积效率为0.9和0.95。试求泵的实际流量，压头和轴功率。解：三动泵理论平均流量QT=3ASnr=3×π/4×(0.07)2×0.025×200=0.52m3/min实际流量Q=ηQT=0.95×0.52=0.494m3/min泵的压头H=△P/ρg+△u2/2g+ΣHf+Z取△u2/2g=0=△P/ρg+ΣHf+Z=1.28×106/1250×9.81+2+10=116.38m轴功率N=HQρ/102η=13.05Kw9．用一往复泵将密度为1200kg/m³的液体从A池输送到B槽中，A池和B槽液面上方均为大气压。往复泵的流量为5m³/h。输送开始时，B槽和A池的液面高度差为10m。输送过程中，A池液面不断下降，B槽液面不断上升。输送管径为30mm，长为15m（包括局部阻力当量长度）。A池截面积为12m²，B槽截面积为4.15m²。液体在管中流动时摩擦系数为0.04。试求把25m³液体从A池输送到B槽所需的能量。解：列出此往复泵输送的管路特性方程Ηe=K+BQe2而K=△P/ρg+△u2/2g+Z∵A，B槽上方均大气压∴△P/ρg=0，△u2/2g=0 在输送开始时，h0=10m输送完毕后A池液面下降：25/12=2.01mB池液面上升：25/4.15=6.1m∴h=10+2.01+6.1=18.11mB=λ•(ι+Σιe)/d·1/2g(3600A)2=0.4×15/0.03×1/[(3600×π/4×0.032)2×2×9.81]=0.157输送开始时管路的特性方程Ηe=10+0.157Qe2输送完毕时管路的特性方程Ηe"=18.4+0.157Qe2取平均压头Η平均=(Ηe+Ηe")/2=（10+0.157Qe2+8.4+0.157Qe2）/2，Qe=5m3/s=18m输送所需要的时间τ=V/Q=25/5=5h=18000输送有效功率Ne=HQρg=18×5/3600×1200×9.81=294.3所需要的能量W=Neτ=5.3×106J=5300KJ10.已知空气的最大输送量为14500kg/h，在最大风量下输送系统所需的风压为1600Pa（以风机进口状态级计）。由于工艺条件的呀求。风机进口与温度为40℃，真空度为196Pa的设备相连。试选合适的离心通风机。当地大气压为93.3kPa。解：输送洁净空气应选用4-72-11型通风机40℃，真空度为196Pa时空气的密度ρ"=MP/RT=1.04Kg/m3将输送系统的风压HT"按HT=HT"ρ/ρ"HT=1600×1.2/1.04=1850.72m输送的体积流量Q=Qm/ρ=14500/1.04=13942.31m3/h根据输送量和风压选择4-72-11No6c型可以满足要求其特性参数为转速(r/min)风压(Pa)风量(m3/h)效率(％)功率（Kw）20001941.8141009110.011.15℃的空气直接由大气进入风机在通过内径为800mm的水平管道送到炉底，炉底表压为 10kPa。空气输送量为20000m/h（进口状态计），管长为100m（包括局部阻力当量长度），管壁绝对粗糙度可取为0.3mm。现库存一台离心通风机，其性能如下所示。核算此风机是否合用？当地大气压为101.33kPa。转速，r/min风压，Pa风量，m³/h14501265021800解：输送系统的风压HT"=（Z2–Z1）ρg+P2–P1+（u22-u12）/2+ρΣhf∵水平管道输送，∴Z2–Z1=0，（u22-u12）/2=0空气的流动速度u=Q/A=20000/（π/4·0.82×3600）=11.06m/s查本书附图可得15℃空气的粘度μ=1.79×10-3Pa·s，密度ρ=1.226Kg/m3Re=duρ/μ=0.8×1.226×11.06/1.79×10-3=6059.1ε/d=0.3/800=0.000375根据Re-ε/d图可以得到其相对粗糙度λ=0.0365∴Σhf=λ•(ι+Σιe)/d•u2/2=0.0365×100/0.8×11.062/2=279.1输送系统风压HT"=P2–P1+ρΣhf=10.8×103+1.226×279.1=11142.12Pa<12650Pa且Q=20000〈21800∴此风机合用12.某单级双缸双动空气压缩机，活塞直径为300mm，冲程为200mm，每分钟往复480次。压缩机的吸气压强为9.807×104Pa，排气压强为34.32×104Pa。试计算该压缩机的排气量和轴功率。假设汽缸的余隙系数为8%，排气系数为容积系数的85%，绝热总效率为0.7。空气的绝热指数为1.4。解：双缸双动压缩机吸气量Vmin=（4A-a）snr 活杆面积与活塞面积相比可以略去不计∴吸收量Vmin"=4Asnr=4×π/4×0.32×0.2×480=27.13m3/min压缩机容积系数λ0=1-ε[(P2/P1)1/r-1]=1-0.08[（34.32/9.80）1/1.4-1]=0.8843λd=0.85λ0=0.7516∴排气量Vmin=λd•Vmin"=20.39m3/min实际压缩功率Na=P1Vmin·к/（к-1）[(P2/P1)κ/(κ-1)–1]=50.19Kw该压缩机的轴功率N=Na/ηa=50.19/0.7=71.7Kw13.用三级压缩把20℃的空气从98.07×10³kPa压缩到62.8×105Pa。设中间冷却器能把送到最后一级的空气冷却到20℃，各级压缩比相同。试求：（1）.在各级的活塞冲程及往复次数相同情况下，各级汽缸直径比。（2）三级压缩消耗的理论功（按绝热过程考虑。空气绝热指数为1.4，并以1kg计）。分析：多级压缩机的工作原理：每一级排出口处的压强多时上一级的四倍，因此每一级空气的流量为上一次的0.25倍解：⑴各级的活塞冲程及往复次数相同压缩机总的压缩比χ=（P2/P1）1/3=4V1：V2：V3=A1：A2：A3=16：4：1⑵20℃时1Kg空气的体积V1=mRT/MP=1×8.315×293/(29×98.07)=0.8566m3根据W=P1V1·iκ/（κ-1）·[(P2/P1)(к-1)/iк-1]=98.07×10×0.8566×3×1.4/0.4×（40.4/1.4-1）=428.7KJ第三章机械分离和固体流态化 1.试样500g，作为筛分分析，所用筛号及筛孔尺寸见本题附表中第一，二列，筛析后称取各号筛面的颗粒截留量于本题附表中第三列，试求颗粒群的平均直径。筛号筛孔尺寸，mm截留面，g筛号筛孔尺寸,mm截留面，g101.6510650.20860.0141.16820.01000.14730.0200.83340.01500.10415.0280.58980.02000.07410.0350.4171302700.0535.0480.295110共计500解：先计算筛分直径d1=（d10+d14）/2=1.4095，d2=（d14+d20）/2=1.084同理可以计算出d3=0.711，d4=0.503，d5=0.356，d6=0.252d7=0.1775，d8=0.1225，d9=0.089，d10=0.0635根据颗粒平均比表面积直径公式1/da=1/GΣGi/d得到1/GΣGi/d=1/500（20/1.4095+40/1.084+80/0.711+130/0.503+110/0.356+60/0.252+30/0.1775+15/0.1255+10/0.089+5/0.0635）=2.899颗粒平均直径相当于平均比表面积直径，即颗粒平均直径d=da=1/2.899=0.3452.密度为2650kg/m³的球型石英颗粒在20℃空气中自由沉降，计算服从斯托克斯公式的最大颗粒直径及服从牛顿公式的最小颗粒直径。解：（1）服从斯托克斯公式查有关数据手册得到20℃时空气的密度ρ=1.205Kg/m3，粘度μ=1.81×10-5Pa·s要使颗粒服从斯托克斯公式，必须满足Re〈1即Re=dutρ/μ〈1，而ut=d2（ρs-ρ）g/18μ由此可以得到d3〈18u2/（ρs-ρ）ρg∴最大颗粒直径dmin=[18u2/（ρs-ρ）ρg]1/3=[18×（1.81×10-5）2/（2650-1.205）×9.81×1.205]1/3 =0.573×10-4m=57.3μm要使颗粒服从牛顿公式，必须满足103〈Re〈2×103即103〈Re=dutρ/μ〈2×103，而ut=1.74[d（ρs-ρ）g/ρ]由此可以得到d3〉106μ2/［1.742ρ（ρs-ρ）g］∴最小直径dmin=0.001512m=1512μm3.在底面积为40m²的除尘室内回收气体中的球形固体颗粒。气体的处理量为3600m³/h，固体的密度ρs=3600kg/m³，操作条件下气体的密度ρ=1.06kg/m³，粘度为3.4×10-5Pa•s。试求理论上完全除去的最小颗粒直径。解：根据生产能力计算出沉降速度ut=Vs/bι=3600/40m/h=0.025m/s假设气体流处在滞流区则可以按ut=d2（ρs-ρ）g/18μ进行计算∴d2=18μ/（ρs-ρ）g·ut可以得到d=0.175×10-4m核算Re=dutρ/μ〈1，符合假设的滞流区∴能完全除去的颗粒的最小直径d=0.175×10-4m=17.5μm4.一多层降尘室除去炉气中的矿尘。矿尘最小粒径为8µm，密度为4000kg/m³。除尘室长4.1m，宽1.8m，高4.2m，气体温度为427℃，粘度为3.4Pa•s，密度为0.5kg/m³。若每小时的炉气量为2160标准m³，试确定降尘室内隔板的间距及层数。解：假设沉降在滞流区，按ut=d2（ρs-ρ）g/18μ计算其沉降速度ut=(8×10-6)2×(4000-0.5)×9.8/(18×3.4×10-5)=41×10-4m/s核算Re=dutρ/μ〈1，符合假设的滞流区把标准生产能力换算成47℃时的生产能力Vs=V(273+427)/273=5538.46m3/h由Vs=blut（n-1）得n=Vs/blut-1=5538.46/（4.1×1.8×41×10-4×3600）-1=50.814–1=49.8 取n=50层，板间距△h=H/（n+1）=4.2/51=0.0824m=82.4mm5.含尘气体中尘粒的密度为2300kg/m³，气体流量为1000m³/h，粘度为3.6×10-5Pa•s密度为0.674kg/m³，采用如图3-8所示的标准型旋风分离器进行除尘。若分离器圆筒直径为0.4m，试估算其临界直径，分割粒径及压强降。解：(1)临界直径选用标准旋风分离器Ne=5，ξ=8.0B=D/4，h=D/2由Vs=bhui得Bh=D/4·D/2=Vs/ui∴ui=8Vs/D2根据dc=[9μB/(πNeρsui)]1/2计算颗粒的临界直径∴dc=[9×3.6×10×0.25×0.4/(3.14×5×2300×13.889)]1/2=8.04×10-6m=8.04μm（2）分割粒径根据d50=0.27[μD/ut（ρs-ρ）]1/2计算颗粒的分割粒径∴d50=0.27[3.6×10-5×0.4/(13.889×2300)]1/2=0.00573×10-3m=5.73μm（3）压强降根据△P=ξ·ρui2/2计算压强降∴△P=8.0×0.674×13.8892/2=520Pa6.风分离器出口气体含尘量为0.7×10-3kg/标准m³，气体流量为5000标准m³/h，每小时捕集下来的灰尘量为21.5kg。出口气体中的-灰尘粒度分布及捕集下来的灰尘粒度分布测定结果列于本题附图表中：粒径范围0-55-1010-2020-3030-4040-50>50在出口灰尘中所占的质量分率%16252920721在捕集的灰尘中所占的质量分率%4.41126.62018.711.33试求：（1）除尘效率（2）绘出该旋风分离器的粒级效率曲线。 解：出口气体中每小时产生的灰尘量：0.7×10-3×5000=2.35Kg除尘效率：η0=21.5/（21.5+3.5）=0.86=86％计算出每一小段范围捏颗粒的粒级效率ηP1=21.5×4.4/（21.5×4.4+3.5×16）=62.8％ηP2=21.5×11/（21.5×11+3.5×25）=73.0％ηP3=21.5×26.6/（21.5×26.6+3.5×29）=84.93％ηP4=86％ηP5=94.26％ηP6=97.2％ηP7=94.85％绘出粒级效率曲线如图所示7.验室用一片过滤面积为0.1m³的滤叶对某种颗粒在水中的悬浮液进行实验，滤叶内部真空读为500mmHg，过滤5min的滤液1L，又过滤5min的滤液0.6L，若再过滤5min得滤液多少？分析：此题关键是要得到虚拟滤液体积，这就需要充分利用已知条件，列方方程求解解：⑴虚拟滤液体积由过滤方程式V2+2VVe=KA2θ过滤5min得滤液1L（1×10-3）2+2×10-3Ve=KA2×5①过滤10min得滤液1.6L（1.6×10-3）2+2×1.6×10-3Ve=KA2×10②由①②式可以得到虚拟滤液体积Ve=0.7×10-3KA2=0.396⑵过滤15分钟假设过滤15分钟得滤液V"V"2+2V"Ve=KA2θ"V"2+2×0.7×10-3V"=5×0.396V"=2.073×10-3∴再过滤5min得滤液V=2.073×10-3-1.6×10-3=0.473×10-3m30.473L 8.以小型板框压滤机对碳酸钙颗粒在水中的悬浮液进行过滤实验，测得数据列于本题附表中：已知过滤面积为0.093m2，试求：（1）过滤压强差为103.0kPa时的过滤常数K,qe及θe(2)滤饼的压缩指数s；（3）若滤布阻力不变，试写出此滤浆在过滤压强差为196.2kPa时的过滤方程式。解：⑴过滤常数K,qe及θe根据q2+2qqe=Kθ，和q=V/A，带入表中的数据（2.27/93）2+2qe×2.27/93=50K①（9.1/93）2+2qe×9.1/93=660K②由①②两式可得qe=3.81×10-3K=1.564×10-5∵qe2=Kθe∴θe=qe2/K=0.929⑵滤饼的压缩指数s同理在△P=343.4Kpa时，由上式带入表中数据得（2.27/93）2+2qe"×2.27/93=17.1K"③（9.1/93）2+2qe×9.1/93=233K"④得到qe=3.1×10-3K=4.37×10-5利用lgK=（1-s）lg△P+lg2k，对压强差为103.0Kpa和343.4Kpa时的过滤常数K取对数差得lg（K/K"）=（1-s）lg（△P/△P"）∴1-s=0.8532，即压缩指数s=0.1468⑶过滤方程式在过滤压强差为196.2Kpa时lg（K/K""）=（1-s）lg（△P/△P""）∴lg（1.564/K""）=0.8532×lg（103/196.2""得K""=2.71×10-5qe""=（qe"+qe"）/2=（3.81+3.1）×10-3/2=3.5×10-3∵qe2=Kθe∴θe""=qe""2/K=3.5×10-3/2.71×10-5 =0.452∴过滤方程式为（q+3.5×10-3）2=2.71×10-5（θ+0.452）9.在实验室中用一个边长0.162m的小型滤框对CaCO3颗粒在水中的悬浮液进行过滤实验。料浆温度为19℃，其中CaCO3固体的质量分率为0.0723。测得每1m3滤饼烘干后的质量为1602kg。在过滤压强差为275800Pa时所的数据列于本题附表：过滤时间θ1.84.27.511.215.420.526.733.441.048.857.767.277.388.7滤液体积V0.20.40.60.81.01.21.41.61.82.02.22.42.62.8试求过滤介质的当量滤液体积Ve，滤饼的比阻r，滤饼的空隙率ε及滤饼颗粒的比表面积α。已知CaCO3颗粒的密度为2930kg/m3，其形状可视为圆球。解：由（V+Ve）2=KA2（θ+θe）两边微分得2（V+Ve）dv=KA2dθdθ/dv=2V/KA2+2Ve/KA2计算出不同过滤时间时的dθ/dv和V，将其数据列表如下V0.40.60.81.01.21.41.61.82.02.22.42.62.8△θ/△v1216.518.52125.23133.5383944.547.550.557作出dθ/dv–V的曲线如图10.用一台BMS50/810-25型板框压滤机过滤某悬浮液，悬浮液中固体质量分率为0.139，固相密度为2200kg/m3，液相为水。每1m³滤饼中含500kg水，其余全为固相。已知操作条件下的过滤常数K=2.72×10-5m/s，q=3.45×10m3/m2。滤框尺寸为810mm×810mm×25mm,共38个框。试求：（1）过滤至滤框内全部充满滤渣所需的时间及所得的滤液体积：（2）过滤完毕用0.8m清水洗涤滤饼，求洗涤时间。洗水温度及表压与滤浆的相同。解：（1）滤框内全部充满滤渣滤饼表面积A=（0.81）2×2×38=49.86m2滤框容积V总=（0.81）2×0.025×38=0.6233m3已知1m3的滤饼中含水：500/1000=0.5m3含固体：1–0.5=0.5m3固体质量：0.5×2200=1100Kg 设产生1m3的滤饼可以得到m0，Kg（V0，m3）的滤液，则0.139=1100/（1100+50+m）∴m0=6313Kg滤液的密度按水的密度考虑V0=0.314m3∴形成0.6233m3的滤饼即滤框全部充满时得到滤液体积V=6.314×0.6233=3.935m3则过滤终了时的单位面积滤液量为q=V/A=3.935/49.86=0.07892m3/m2∵qe2=Kθe∴θe=qe2/K=（3.45×10-3）2/2.72×10-5=0.4376由（q+qe）2=K（θ+θe）得所需的过滤时间为θ=（q+qe）2/K-θe=（0.07892+0.00345）2/2.72×10-5-0.4376=249s⑵洗涤时间Ve=qe×A=3.45×10-3×49.86=0.172由（dv/dθ）Ww=KA2/8（θ+θe）得洗涤速率=2.72×10-5×（49.86）2/8×（3.935+0.172）=205×10-5∴洗涤时间为：0.8/205×10-5=388s11.用叶滤机处理某种悬浮，先以等速过滤20min，得滤液2m3。随即保持当时的压强差再过滤40min，问共得滤液多少m3？若叶滤机每次卸渣重装等全部辅助操作共需20min，求滤液日产量。滤布阻力可以忽略。解：12.在3×105Pa的压强差下对钛白粉在水中的悬浮液进行实验，测的过滤常数K=5×10-5m/s，q=0.01m3/m2 ，又测得饼体积之比v=0.08。现拟用有38个框的BMY50/810-25型板框压滤机处理此料浆，过滤推动力及所用滤布也与实验用的相同。试求：（1）过滤至框内全部充满滤渣所需的时间；（2）过滤完毕以相当与滤液量1/10的清水进行洗涤，求洗涤时间；（3）若每次卸渣重装等全部辅助操作共需15min，求每台过滤机的生产能力（以每小时平均可得多少m3滤饼计）。解：（1）框内全部充满滤渣滤饼表面积A=（0.81）2×2×38=49.86m2滤框容积V总=（0.81）2×0.025×38=0.6233m3总共得到滤液体积V=V总/ν=0.6233/0.08=7.79m3则过滤终了时的单位面积滤液量为q=V/A=7.79/49.86=0.156虚拟过滤时间θe=qe2/K=（0.01）2/5×10-5=2s由（q+qe）2=K（θ+θe）得所需的过滤时间为θ=（q+qe）2/K-θe=（0.156+0.01）2/5×10-5-2=551s⑵洗涤时间Ve=qe×A=0.01×49.86=0.4986由（dv/dθ）Ww=KA2/8（θ+θe）得洗涤速率=5×10-5×（49.86）2/8×（7.79+0.4986）=187.46×10-5清水体积：7.79/10=0.779洗涤时间：0.779/187.46×10-5=416s生产总时间T=551+416+15×60=1867s生产能力Q=3600V总/T=3600×0.6233/1867=1.202m3/h13.某悬浮液中固相质量分率为9.3%，固相密度为3000kg/m3，液相为水。在一小型压滤机中测得此悬浮液的物料特性常数k=1.1×10-4m2（s• atm），滤饼的空隙率为40%。现采用一台GP5-1.75型转筒真空过滤机进行生产（此过滤机的转鼓直径为1.75m，长度为0.98m，过滤面积为5m2，浸没角度为120º），转速为0.5r/min，操作真空度为80.0kPa。已知滤饼不可压缩，过滤介质可以忽略。试求此过滤机的生产能力及滤饼厚度。解：形成的1m的滤饼中含液相：0.4m3固相：0.6m3设产生1m3的滤饼可以得到m0，Kg（V0，m3）的滤液，则0.093=0.6×3000/（0.6×3000+0.4×103+m0）∴m0=17154.84Kg滤液的密度按水的密度考虑V0=17.155m3由K=2k△P得过滤常数K=2×1.1×10-4×80.1/101.5=17.36×10-5过滤机每转一周的过滤时间θ=60ψ/n=60×120/0.5×360=40s∵介质阻力忽略∴Ve=0，θe=0∴转筒每转一周所的滤液体积V液=（KA2θ）1/2=（17.36×52×40）1/2=0.4167m3生产能力Q=nV=0.5×60×0.4167=12.51m3/h每转一周所得的滤饼的体积V饼=0.4167/17.155=0.02429m3滤饼的厚度δ=V饼/A=0.02429/5=0.00486m=4.86mm14.用板框过滤机在恒压差下过滤某种悬浮液，滤框边长为0.65m，已测得操作条件下的有关参数为：K=6×10-5m2/s，qe=0.01m3/m2滤液。滤饼不要求洗涤，其它辅助时间为20min，要求过滤机的生产能力为9m³/h，试求：（1）至少需要几个滤框n？（2）框的厚度L。解：设要得到Vm3的滤液需要的时间为θ，则由（V+Ve）2=KA2（θ+θe）θ=（V+Ve）2/KA2-θe =（V+qeA）2/KA2-qe2/K板框过滤机的生产能力=3600V/（Q+QD）=9∴Q+QD=400V即（V+qeA）2/KA2-qe2/K+20×60×9=400V（V+0.01A）2/6×10-5A2+10800=400V①而总过滤面积A=（0.65）2×2×n=0.845n②联立①②可得210V2+（3.55n–3.6n2）V+10.8n2=0③∴△=（3.55n–3.6n2）2-4×210×10.8n2≥0n≥27.44取n=28即需要28块板将n=28带入③式可得到滤液体积V=7.8m3∴滤饼体积7.8×0.1=0.78m3设滤框的厚度为L则（0.65）2×L×28=0.78∴L=0.066m=66mm15.已知苯酐生产的催化剂用量为37400kg，床径为3.34m，进入设备的气速为0.4m/s，气体密度为1.19kg/m3。采用侧缝锥帽型分布板，求分布板的开孔率。解：16.平均粒径为0.3mm的氯化钾球型颗粒在单层圆筒形流化床干燥器中进行流化干燥。固体密度=1980kg/m3。取流化速度颗粒带出速度的78%，试求适宜的流化速度和流化数。介质可按60℃的常压空气查取物性参数。解：查有关物性手册60℃，常压空气的密度ρ=1.06Kg/m3，粘度µ=2.01×10-5重力沉降的过滤常数K=d[ρ（ρs-ρ）g/2μ2]1/3=7.71∵2.6250mmQ==（tw–t）/R2=325.29W未加保温层时，即r2=r1∴Q，=（tw–t）/R2，αT，=9.4+0.052（tw–t）=14.6R2，=1/αTSo=1/αT2πr2L∴Q，=114.61W∴未加保温时的热损失小些，且保温曾厚度越大热损失越大。6.在并流换热器中，用水冷却油。水的进出口温度分别为15℃，40℃，油的进出口温度分别为150℃和100℃。现生产任务要求油的出口温度降至80℃℃，假设油和水的流量，进出口温度及物性不变，若换热器的管长为1m，试求此换热器的管长增至若干米才能满足要求。设换热器的热损失可忽略。解：根据题意列出关系式：热流体（油）：T1=150℃→T2=100℃冷流体（水）：t1=15℃→t2=40℃现在要求：热流体（油）：T1=150℃→T2=80℃冷流体（水）：t1=15℃→t2=？开始：Q=WhCph（T1-T2）=50WhCph=WcCpc（t2-t1）=25WcCpc=K0S0ΔtmΔtm=（Δt1-Δt2）/ln（Δt1/Δt2）=（135-60）/ln（135/60）=92.49改变后：Q，=WhCph（T1-T2）=700WhCph =WcCpc（t2，-t1）=（t2，-15）WcCpc=K0S0，Δtm，∴25/（t2，-15）=50/70∴t2，=50℃Δtm，=（Δt1-Δt2，）/ln（Δt1/Δt2，）=69.81∴Q/Q*=K0SΔtm/K0S，Δtm，=LΔtm/L，Δtm，=50/70∴L，=1.85L=1.85m7.重油和原由在单程套换热器中呈并流流动，粮站油的初温分别为243℃和128℃；终温分别为167℃和157℃。若维持两种油的流量和初温不变，而将两流体改为逆流，试求此时流体的平均温度差及他们的终温。假设在两种流动情况下，流体的无性和总传热系数均不变，换热器的热损失可以忽略。解：由题意得：并流时：热流体（重油）：T1=243℃→T2=167℃冷流体（原油）：t1=128℃→t2=157℃∴Q=WhCph（T1-T2）=76WhCph=WcCpc（t2-t1）=29WcCpc=K0S0ΔtmΔtm=（Δt1-Δt2）/ln（Δt1/Δt2）=43改为逆流后：热流体（重油）：T1=243℃→T2，=？冷流体（原油）：t2，=？←t1=128℃同理：Q，=WhCph（T1-T2，）=（243-T2，）WhCph=WcCpc（t2，-t1）=（t2，-128）WcCpc=K0S0，Δtm，∴29/（t2，-128）=76/（243-T2，）∴T2，=578.45-2.62t2，--------（1）Δtm，=[（243-t2，）-（T2，-128）]/ln[（243-t2，）/（T2，-128）]-------（2）又Q/Q*=Δtm/Δtm，=29/（t2，-128）---------（3）由（1）（2）（3）解得t2，=161.41℃T2，=155.443℃Δtm，=49.5℃ 8.在下列各种管式换热器中，某溶液在管内流动并由20℃加热到50℃。加热介质在壳方流动，其进出口温度分别为100℃和60℃，试求下面各种情况下的平均温度差。(1)壳方和管方均为单程的换热器。设两流体为逆流流动。(2)壳方和管方分别为单程和四程的换热器。(3)壳方和管方分别为二程和四程的换热器。解：（1）热流体：T1=100℃→T2=60℃冷流体：t2=50℃←t1=20℃Δt1=50℃Δt2=40℃∴Δtm=（Δt1-Δt2）/ln（Δt1/Δt2）=44.8℃（2）壳方和管方分别为单程和四程，则需计算平均温度差校正系数ψΔt，由已知条件计算得ψΔt=0.891∴Δtm，=ψΔtΔtm=0.891×44.8=39.9℃（3）查图得，ψΔt=0.97∴Δtm，=ψΔtΔtm=0.97×44.8=43.5℃9.在逆流换热器中，用初温为20℃的水将1.25kg/s的液体（比热容为1.9kJ/kg•℃，密度为850kg/m），由80℃冷却到30℃。换热器的列管直径为ф252.5mm，水走管方。水侧和液体侧的对流传热系数分别为0.85W/（m2•℃）和1.70W/（m2•℃）。污垢热阻忽略。若水的出口温度不能高于50℃，试求换热器的传热面积。解：热流体：T1=80℃→T2=30℃冷流体：t2=50℃←t1=20℃Δt1=30℃Δt2=10℃∴Δtm=（Δt1-Δt2）/ln（Δt1/Δt2）=18.205℃Q=WhCph（T1-T2）=1.9×10³×1.25×50=118.75W又Q=K0S0Δtm，其中1/K0=d0/αidi+1/α0解得K0=0.486×10³m2•℃/W∴0.486×10³×18.205S0=118.75×10³∴S0=13.4m³10.在列管式换热器中用冷水冷却油。水在直径为ф192mm的列管内流动。已知管内水侧对流传热系数为3490W/（m2•℃），管外油侧对流传热系数为258W/（m2•℃ ）。换热器用一段时间后，管壁两侧均有污垢形成，水侧污垢热阻为0.00026m2•℃/W，油侧污垢热阻0.000176m2•℃/W。管壁导热系数λ为45W/（m•℃），试求：（1）基于管外表面的总传热系数；（2）产生污垢后热阻增加的百分比。解：（1）1/K0=d0/αidi+1/α0+Rsid0/di+Rs0+bd0/λdm=19/（3490×15）+0.00026×19/15+0.000176+（0.002×19）/（45×16.9）+1/258∴K0=208m2•℃/W（2）产生污垢后增加的总热阻：Rsid0/di+Rs0=0.00026×19/15+0.000176=0.00050533产生污垢前的总热阻：d0/αidi+1/α0+bd0/λdm=19/（3490×15）+（0.002×19）/（45×16.9）+1/258=0.0043∴增加的百分比为：0.00050533/0.00429=11.8%11.在一传热面积为50m2的单程列管式换热器中，用水冷却某种溶液。两流体呈逆流流动。冷水的流量为33000kg/h，温度由20℃升至38℃。溶液的温度由110℃降至60℃。若换热器清洗后，在两流体的流量和进出口温度不变的情况下，冷水出口温度增至45℃。试估算换热器清洗前后传热面两侧的总污垢热阻。假设（1）两种情况下，流体物性可视为不变，水的比热容可取4.187kJ/（kg•℃）；（2）可按平壁处理，两种工况下αi和α0分别相同；（3）忽略管壁热阻和热损失。解：换洗前：热流体：T1=110℃→T2=60℃冷流体：t2=38℃←t1=20℃Δt1=72℃Δt2=40℃∴Δtm=（Δt1-Δt2）/ln（Δt1/Δt2）=54.4℃Q=WhCph（T1-T2）=50WhCph=WcCpc（t2-t1）=18WcCpc=K0S0Δtm=54.4K0S0代入数据计算得K0=254W/（m2•℃）换洗后：：热流体：T1=110℃→T2=60℃冷流体：t2=38℃←t1=20℃Δt1=72℃Δt2=40℃ ∴Δtm=（Δt1-Δt2）/ln（Δt1/Δt2）=54.4℃Q=WhCph（T1-T2）=（100-T2）WhCph=WcCpc（t2-t1）=25WcCpc=K0，S0Δtm，∴50/（100-T2）=18/25→T2=40.56℃∴Δtm，=（Δt1，-Δt2，）/ln（Δt1，/Δt2，）=35℃Q==WcCpc（t2-t1）=K0，S0Δtm，代入数据计算得K0，=548.3W/（m2•℃）∴总污垢热阻为：1/K0-1/K0，=1/245-1/548.3=2.1×10-3m2•℃/W12.在一单程列管换热器中，用饱和蒸汽加热原料油。温度为160℃饱和蒸汽在壳程冷凝（排出时为饱和液体），原料油在管程流动，并由20℃加热到106℃，列管换热器尺寸为：列管直径为ф19×2mm，管长为4m，共25根管子。若换热器的传热量为125Kw，蒸汽冷凝传热系数为7000W/（m2•℃），油侧污垢热阻可去为0.0005m2•℃/W，管壁热阻和蒸汽侧垢层热阻可忽略，试求管内油侧对流传热系数。又若有的流速增加一倍，此时若换热器的总传热系数为原来的1.75倍，试求油的出口温度。假设油的物性不变。解：1/K0=d0/αidi+1/αi+Rsid0/di，又K0=Q/S0Δtm其中S=25×3.14×19×10³×4=5.97Δtm=（Δt1-Δt2）/ln（Δt1/Δt2）=90.27℃∴K0=125×10³/（5.97×90.27）=232.1W/（m2•℃）可以解得αi=359.5W/（m2•℃）改变流速后：K0，=1.75K0=406.2W/（m2•℃）Q*=2Q（t2，-t1）/（t2-t1）=125×10³（t2，-20）/86又Δtm，=[（T-t1）-（T-t2，）]/ln[（T-t1）/（T-t2，）]=Q，/K0S可以解得t2，=99.2℃ 13.90℃的正丁醇在逆流换热器中被冷却到50℃。换热器的传热面积为6m2，总传热系数为230W/（m2•℃）。若正丁醇的流量为1930kg/h，冷却介质为18℃的水。试求：（1）冷却水的出口温度；（2）冷却水的消耗量，以m³/h表示。解：由传热方程式Q=K0SΔtm=WhCph（T1-T2）查表得70℃的正丁醇的比热为3.06×10³J/（kg•℃）∴Q=1930/3600×3.06×10³×（90-50）=65.5×10³J/sΔtm=Q/K0S=65.5×10³/（230×6）=47.5℃Δtm=（Δt1-Δt2）/lnΔt1/Δt2=[（90-t2）-（50-18）]/ln[（90-t2）/（50-18）]试差得t2=22.7℃假定无热阻损失即冷水吸收热量和正丁醇放出热量相等Q=WcCpc（t1-t2），Cpc=4.183kJ/（kg•℃）65.5×10³=4.183×10³Wc（22.7-18）Wc=3.33kg/s∴V=12m³/h14.在逆流换热器中，用冷油冷却热油。油的比热容均为1.68kJ/（kg•℃），热油的流量为3000kg/h，从100℃冷却到25℃。冷油从20℃加热到40℃。已知总传热系数K0。随热油温度T变化如下：热油温度T，℃1008060403025总传热系数K0，W/（m2•℃）355350340310230160试求换热器的传热面积。解：热油：100℃→25℃冷油：40℃→20℃分批计算：热流体从100℃→80℃。80℃→60℃，60℃→40℃，40℃→30℃，30℃→25℃时的传热量Q1，Q2，Q3，Q4，Q5及传热面积S1S2S3S4S5总传热面积S=S1+S2+S3+S4+S5冷流体的流量：由WhCphΔT=WcCpcΔt得Wc=11250kg/h从100℃→80℃的传热面积3000×1.68×20=11250×1.68×（40-t1）→t1=34.6℃∵Δt1/Δt2=60/45.3<2∴Δtm1=(Δt1+Δt2)=52.6℃Q1=3000/3600×1.68×10³×20=28×10³ 取K01=（355+350）=352.5W/（m2•℃）S1=Q1/K01Δtm1=28×10³/（352.5×52.6）=1.508同理得S2=2.1358S3=3.8216S4=4.3351S5=5.279∴S=17m215.在一逆流套管中，冷，热流体进行热交换。两流体的进出口温度分别为t1=20℃，t2=85℃，T1=100℃，T2=70℃。当冷流体的流量增加一倍时，试求两流体的出口温度和传热量的变化情况。假设两种情况下总传热系数可视为相同，换热器热损失可忽略。解：热：T1=100℃→T2=70℃冷：t2=85℃←t1=2İ℃ဠ热流体放热Q放=WhCph（T1-T2）冷流体吸热Q吸=WcCpc（t1-t2）"䀠由传热Q=K0SΔtm︌Δtm=[（T2-t1）-（T1-t2）]/ln[（T2-t1ဠ）/（T1-t2）]=29.07℃∴Q=29.07K0S冷流体流量增加一倍后：热：T1=100℃→T2，冷：t2，←t1=20℃而K0，S不变，∴Q=Q*Δtm*/Δtm∴Q*=Q（t2，+T2，-120）/29.07ln[（T2，-20）/（100-t2，）]Q放,=[(100-T2，)/30]Q放Q吸,=[2(t2，-20)/65]Q吸∴Q*=Q（t2，+T2，-120）/29.07ln[（T2，-20）/（100-t2，）]=Q放,=[(100-T2，)/30]Q放=Q吸,=[2(t2，-20)/65]Q吸用试差法得T2，=59.8℃t2，=63.5℃∴Q/Q*=30/（100-T2，）=1.3416.试用因次分析方法推导壁面和流体间自然对流传热系数α的准数方程式。已知α为下列变量函数，即α=f（λ，cp，ρ，μ，βgΔt，l）解：（1）先列出各物理量的因次，如下表所示αλCPρμρβg△tιM/Tθ3LM/Tθ3L2/Tθ2M/L2M/LθM/L2θ2L （2）选择4个共同的物理量：λ，ι，CP，μ（3）因次分析π1=ιaλbCPcμdαπ2=ιeλfCPgμhρπ3=ιiλjAPkμlρƲg△tπ1，π2，π3为无因次‴M0L0T0θ0=La（LM/Tθ3）b（L2/Tθ2뼉c（M/Lθ）d（M/Tθ3）对长度L：a+䀠b+2c∓d=0对质量M：b+d+1=0对时间θ：-3b-2c–d–3=0对温度T：-b–c–1=0解得a=1，b=-1，c=0，d=0∴π1=ιλ-1α=Nuπ2=CPμ/λ=Prπ3=ι3ρ2βg△t/μ2=Gr由α=f（λ，CP，ρ，μ，ρβg△t，ι）得Nu=f（Gr，Pr）17.在套管换热器中，一定流量的水在管内流动，温度从25℃升高到75℃，并测得内管水侧的对流传热系数为2000W/（m2•℃）。若相同体积流量的油品通过该换热器的内管而被加热，试汃此时内管内油侧对流传热系異。假定两种懅况下流体呈湍流流动。已知定性温度下物性如下：ρ，kg/m3μ，Pa•scp，kJ/（kg•℃）λ，W/（m•℃）水10000.54×10-34&170.65油品8105&1×10-32.01Р0.15解：∵水为低粘度流体∴α=（0.023λ/di）（diuρ/μ）0.8（cpμ/λ）n流体温度从25℃升到75℃取n=0.4∴α=258.47（diuρ/μ）0.8∴（diuρ/μ）0.8=0.7879油为高粘度液体，采用西德尔和塔特关联式 α，=（0.027λ/di）（diuρ/μ）0.8（cpμ/λ）1/3Ψn取Ψn=1.05∴α，=0.027×0.15（diuρ/μ）0.8[810/（5.1×10）]0.8（2.01×5.1/0.15）1/31.05=203W/（m2•℃）19.98%的硫酸以0.7m/s的速度在套管换热器的环隙内流动，硫酸的平均温度为70℃，内管外壁的平均温度为60℃。换热器的内管直径为Ф25×2.5mm，外管直径为ф51×3mm，试求对流传热的热通量。解：由q=α△t计算对流传热的热通量查本书附录98％的硫酸有关物性常数µ=6.3×10-3Pa·s，CP=1.465KJ/(Kg·℃)，λ=W/(m·℃)当量直径de=4A/b=(d0i2–di02)/(d0i+di0)=(452–252)/(45+25)=20mmRe=deuρ/μ=0.02×0.7×1.836×103/6.3×10-3=4080∵2300<4080<10000∴硫酸在环管中作过渡流先用湍流的西德尔和塔特关联式计算α=0.027•（λ/de）•Re0.8•Pr1/3•Ψu其中Pr=CPμ/λ=取校正系数Φ=1-6×105/Re1.8=0.81α"=0.81α△t=ts–tWww对流热通量q=α"△t=0.81α(ts–tWw)20.温度为90℃甲苯以1500kg/h的流量通过蛇管而被冷却至30℃。蛇管直径为Ф57×3.5mm，弯曲半径为0.6m，试求甲苯对蛇管壁的对流传热系数。解：查有关资料的甲苯在60℃时的有关物性常数μ=0.375×10-3Pa·s，λ=0.143W/（m•℃），ρ=830Kg/m，Cp=1.8376KJ/(Kg·℃)Re=duρ/μ=dQ/Aμ=0.05×1500×4/(3600×π×0.052×0.4×10-3) =26539.3>104属于湍流范围Pr=CPμ/λ=1.8376×0.375/0.1423=4.84α=0.023λ/di×Re0.8·Prn∵甲苯被冷却，取n=0.3计算α=0.023×(0.1423/0.05)×(26539.3)0.8×(4.84)0.3=363.5W/（m2•℃）由于流体在弯管内作强制对其传热系数可由α"=α(1+1.77di/r")来计算∴α"=α(1+1.77di/r")=363.5×（1+1.77×0.05/0.6）=417.14W/（m2•℃）21.常压下温暖男男女女的为120℃的甲烷以10m/s的平均速度在列管换热器的管间沿轴向流动。离开换热器时甲烷的温度为30℃，换热器外壳内径为190mm，管束由37根ф19×2mm的钢管组成，试求甲烷对管臂的对流传热系数。22.室内水平放置表面温度相同，长度相等的两根圆管，管内通有饱和水蒸汽。两管均被空气的自然对流所冷却，假设两管间无相互影响。已知一管直径为另一管的五倍，且两管的（GrPr）值在104—109之间，试求两管热损失的比值。解：空气在水平管外自然对流传热Q=αS△t散热面积S=πdL自然对流系数α=C·(Gr·Pr)n·λ/ι查表对于水平圆管(Gr·Pr)在104–106范围内C=0.53，n=0.25Gr·Pr=ι3ρ2βg△t/μ2×CPμ/λ∴Q=0.53λ×(ρ2CPβg△t/μλ)0.25×d0.75L△t两根圆管长度相等，表面温度相同且都通入的是水蒸气∴其放热量之比Q大/Q小=（d大/d小）075=3.3423.流量为720kg/h的常压饱和水蒸气在直立的列管换热器的列管外冷凝。换热器内列管直径为φ25×2.5mm，长为2m。列管外壁面温度为94℃ 。是按冷凝要求估算换热器的管数（设管内侧传热可满足要求）。换热器热损失可忽略。解：查常压下水蒸气的有关物性数捯：T=100℃λ=68.27×10-2W/（m•℃）r=2258.4kJ/kgμ=0.282×10-3Pa•sρ=958kg/m3由汽化热计算传热速率Q=w•r=720/3600Ö2258.4×耱0³=451.68×10³根据对流传热速率方程Q=αS（䁴s-tw）传热面积S=Q/α（ts tw（∵Re=duρ/μ=dw/Aμ=36.139×10³>1800属于湍流∴α=0.0077（ρ2gλ3/μ2）Re0.4=16908.5∴S=451.68×10³/[16908.5×（100-94）]=4.4522mn=s/πd0L=4.4522/（3.14×0.025×2）=28根24．实验测定列管换热器的总传热系数时，水在换热器的列管内作湍流流动，管外为饱和水蒸气冷凝。列管直径为ф25×2.5mm的钢管组成。当水的流速为1m/s时，测得基于管外表面积的总传热系数K0为2115W/（m2•℃）；若其他条件不变，而水的流速变为1.5m/s时，测得K0为2660W/（m2•℃）。试求蒸汽冷凝传热系数。假设污垢热阻可忽略。解：忽略污垢热阻，得1/K0=d0/αidi+1/α0+bd0/λdm内管水对钢管的热对流传热αi=（0.023λ/di）（diuρ/μ）0.8（cpμ/λ）0.4=u0.8×（0.023λ/di）（diρ/μ）0.8（cpμ/λ）0.4∴两次对流传热系数之比为αi/αi，=（u/u，）0.8=（1/1.5）0.8=0.723------（1）查钢管在55℃的导热系数λ=50W/（m•℃），管壁热阻为：bd0/λdm=0.000055785∴1/2115=5/4αi+1/α0+0.000055785---------（2）1/2660=5/4αi，+1/α0+0.000055785---------（3）由上解得α=14965.7W/（m2•℃）25.两平行的大平板，放置在空气中相距为5mm，一平板的黑度为0.1，温度为350K；另一平板的黑度为0.05，温度为300K。若将第一板加涂层，是其黑度变为0.025，试计算由此引起的传热变化的百分率。假设两板间对流传热可忽略。 解：加涂层前因辐射损失的热量，由式4-111知：Q1-2=C1-2ΨS[（T/1OO）4-（T/100）4]∵本题为平行的大平块∴C1-2=C0/（1/ε1+1/ε2-1）=5.67/（1/0.1+1/0.05-1）=0.1955加涂层后C1-2，=C0/（1/ε1，+1/ε2，-1）=0.096∴ΔQ/Q1-2=（90.1955-0.096）/0.1955=50.9%第五章蒸馏1.已知含苯0.5（摩尔分率）的苯-甲苯混合液，若外压为99kPa，试求该溶液的饱和温度。苯和甲苯的饱和蒸汽压数据见例1-1附表。t（℃）80.1859095100105x0.9620.7480.5520.3860.2360.!1解：利用拉乌尔定律计算气液平衡数据查例1-1附表可的得到不同温度下纯组分苯和甲苯的饱和蒸汽压PB*，Pࡁ*，由于总压P=99kPa，则由x=(P-PB+)/(PQ*-PB*)可得出液相组成，这样就可以得到一组绘平衡t-x图数据。以t=80.1℃为例x=（99-40）/（101.33-40）=0.962同理得到其他温度下液相组成墂下表根据表中数据绘出饱和液体线即泡点线由图可得出当x=0.µ时，相应的温度为92℃2.正戊烷（C5H12）和正己烷（C6H14）的饱和蒸汽压数据列于本题附表，试求P=13.3kPa下该溶液的平衡数据。温度C5H12223.1233.0244.0251.0260.6275.1291.7309.3KC6H14248.2259.1276.9279.0289.0304.8322.8341.9 饱和蒸汽压(kPa)1.32.65.38.013.326.653.2101.3解：根据附表数据得出相同温度下C5H12（A）和C6H14（B）的饱和蒸汽压以t=248.2℃时为例，当t=248.2℃时PB*=1.3kPa查得PA*=6.843kPa得到其他温度下A¸B的饱和蒸汽压如下表t(℃)248251259.1260.6275.1276.9279289291.7304.8309.3PA*(kPa)6.8438.00012.47213.30026.60029.48433.42548.87353.20089.000101.300PB*(kPa)1.3001.6342.6002.8265.0275.3008.00013.30015.69426.60033.250利用拉乌尔定律计算平衡数据平衡液相组成以260.6℃时为例当t=260.6℃时x=(P-PB*)/(PA*-PB*)=（13.3-2.826）/（13.3-2.826）=1平衡气相组成以260.6℃为例当t=260.6℃时y=PA*x/P=13.3×1/13.3=1同理得出其他温度下平衡气液相组成列表如下t(℃)260.6275.1276.9279289x10.38350.33080.02850y10.7670.7330.5240根据平衡数据绘出t-x-y曲线3.利用习题2的数据，计算：⑴相对挥发度；⑵在平均相对挥发度下的x-y数据，并与习题2的结果相比较。解：①计算平均相对挥发度理想溶液相对挥发度α=PA*/PB*计算出各温度下的相对挥发度：t(℃)248.0251.0259.1260.6275.1276.9279.0289.0291.7304.8 309.3α----5.2915.5634.178----取275.1℃和279℃时的α值做平均αm=（5.291+4.178）/2=4.730②按习题2的x数据计算平衡气相组成y的值当x=0.3835时，y=4.73×0.3835/[1+(4.73-1)×0.3835]=0.746同理得到其他y值列表如下t(℃)260.6275.1276.9279289α5.2915.5634.178x10.38350.33080.20850y10.7460.7000.5550③作出新的t-x-y"曲线和原先的t-x-y曲线如图4.在常压下将某原料液组成为0.6（易挥发组分的摩尔）的两组溶液分别进行简单蒸馏和平衡蒸馏，若汽化率为1/3，试求两种情况下的斧液和馏出液组成。假设在操作范围内气液平衡关系可表示为y=0.46x+0.549解：①简单蒸馏由ln(W/F)=∫xxFdx/(y-x)以及气液平衡关系y=0.46x+0.549得ln(W/F)=∫xxFdx/(0.549-0.54x)=0.54ln[(0.549-0.54xF)/(0.549-0.54x)]∵汽化率1-q=1/3则q=2/3即W/F=2/3∴ln(2/3)=0.54ln[(0.549-0.54×0.6)/(0.549-0.54x)]解得x=0.498代入平衡关系式y=0.46x+0.549得y=0.804②平衡蒸馏由物料衡算FxF=Wx+DyD+W=F将W/F=2/3代入得到xF=2x/3+y/3代入平衡关系式得 x=0.509再次代入平衡关系式得y=0.7835.在连续精馏塔中分离由二硫化碳和四硫化碳所组成的混合液。已知原料液流量F为4000kg/h，组成xF为0.3（二硫化碳的质量分率，下同）。若要求釜液组成xW不大于0.05，馏出液回收率为88％。试求馏出液的流量和组分，分别以摩尔流量和摩尔分率表示。解：馏出回收率=DxD/FxF=88％得馏出液的质量流量DxD=FxF88％=4000×0.3×0.88=1056kg/h结合物料衡算FxF=WxW+DxDD+W=F得xD=0.943馏出液的摩尔流量1056/(76×0.943)=14.7kmol/h以摩尔分率表示馏出液组成xD=(0.943/76)/[(0.943/76)+(0.057/154)]=0.976.在常压操作的连续精馏塔中分离喊甲醇0.4与说.6（均为摩尔分率）的溶液，试求以下各种进料状况下的q值。（1）进料温度40℃；（2）泡点进料；（3）饱和蒸汽进料。常压下甲醇-水溶液的平衡数据列于本题附表中。温度t液相中甲醇的气相中甲醇的温度t液相中甲醇的气相中甲醇的℃摩尔分率摩尔分率℃摩尔分率摩尔分率1000.00.075.30.400.72996.40.020.13473.10.500.77993.50.040.23471.20.600.82591.20.060.30469.30.700.87089.30.080.36567.60.800.91587.70.100.41866.00.900.95884.40.150.51765.00.950.97981.70.200.57964.01.01.078.00.300.665解：（1）进料温度40℃75.3℃时，甲醇的汽化潜热r1=825kJ/kg 水蒸汽的汽化潜热r2=2313.6kJ/kg57.6℃时，甲醇的比热CV1=2.784kJ/(kg·℃)水蒸汽的比热CV2=4.178kJ/(kg·℃)查附表给出数据当xA=0.4时，平衡温度t=75.3℃∴40℃进料为冷液体进料即将1mol进料变成饱和蒸汽所需热量包括两部分一部分是将40℃冷液体变成饱和液体的热量Q1，二是将75.3℃饱和液体变成气体所需要的汽化潜热Q2，即q=（Q1+Q2）/Q2=1+（Q1/Q2）Q1=0.4×32×2.784×（75.3-40）=2850.748kJ/kgQ2=825×0.4×32+2313.6×0.6×18=35546.88kJ/kg∴q=1+（Q1/Q2）=1.08（2）泡点进料泡点迋料即为饱和液体进料∴q=1（3）饱和蒸汽进料q=07.对习题6中的溶液，若原料液流量为100kmol/h，馏出液组成为0.95，釜沲组成为0.04（以上均为易挥发组分皀摩尔分率，回流比为2.5，试求产品的流量ﴌ精馏段的下降液体流量和提馏段的上升蒸汽流量。假设塔内气液相均为恒摩尔流。解：⑀产品的流量由物料衡算FxF=WxW+DxDD+W=F代入数据得W=20.44kmol/h∴产品流量D=100–60.44=39.56kmol/h②精馏段的下降液体流量LL=DR=2.5×39.56=98.9kmol/h③提馏段的上升蒸汽流量V"40℃进料q=1.08V=V"+（1-q）F=D（1+R）=138.46kmol/h∴V"=146.46kmol/h 8.某连续精馏操作中，已知精馏段y=0.723x+0.263；提馏段y=1.25x–0.0187若原料液于露点温度下进入精馏塔中，试求原料液，馏出液和釜残液的组成及回流比。解：露点进料q=0即精馏段y=0.723x+0.263过（xD，xD）∴xD=0.949提馏段y=1.25x–0.0187过（xW，xW）∴xW=0.0748精馏段与y轴交于[0，xD/（R+1）]即xD/（R+1）=0.263∴R=2.61连立精馏段与提馏段操作线得到交点坐标为（0.5345，0.6490）∴xF=0.6499.在常压连续精馏塔中，分离苯和甲苯的混合溶液。若原料为饱和液体，其中含苯0.5（摩尔分率，下同）。塔顶馏出液组成为0.9，塔底釜残液组成为0.1，回流比为2.0，试求理论板层数和加料板位置。苯-甲苯平衡数据见例1-1。解：常压下苯-甲苯相对挥发度α=2.46精馏段操作线方程y=Rx/（R+1）=2x/3+0.9/3=2x/3+0.3精馏段y1=xD=0.9由平衡关系式y=αx/[1+(α-1)x]得x1=0.7853再由精馏段操作线方程y=2x/3+0.3得y2=0.8236依次得到x2=0.6549y3=0.7366x3=0.5320y4=0.6547x4=0.4353∵x4﹤xF=0.5