华中科技大学材料力学课后习题解答.pdf 76页

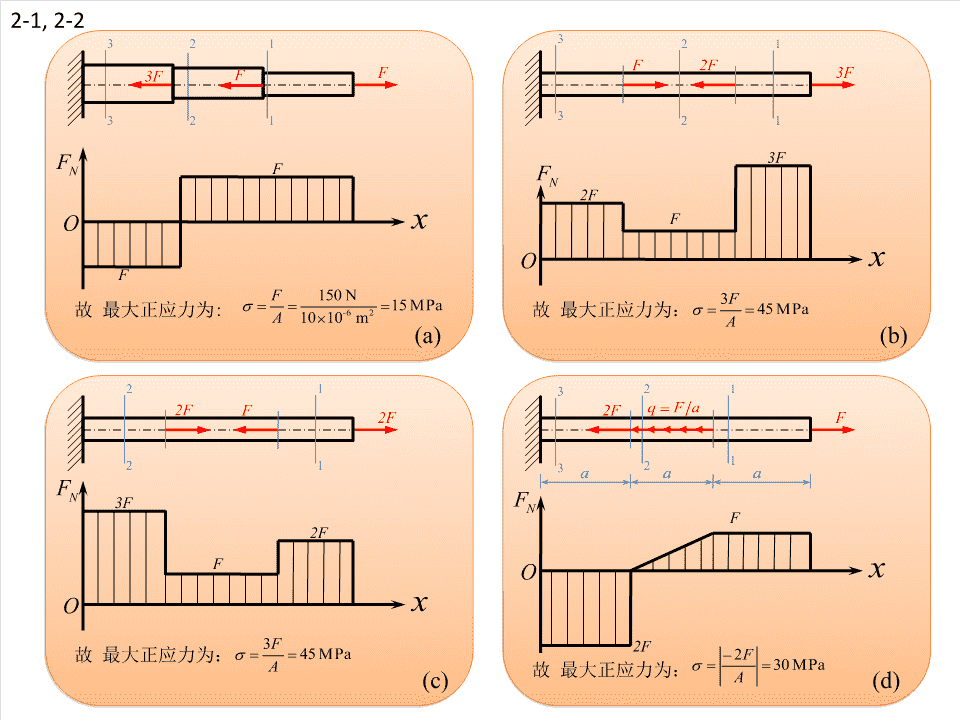
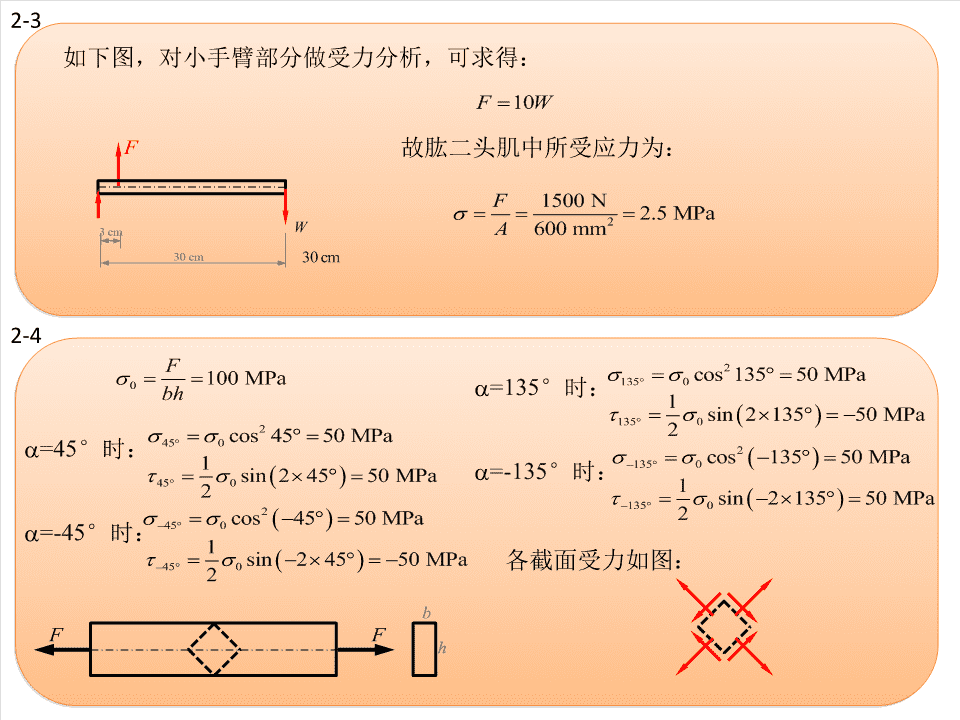
'第二版《材料力学》习题解答（华中科大版倪樵主编）第二章至第七章 2-1,2-2332121F2F3FFF3F332121F3FNFFN2FOxFOxFF150N3F故最大正应力为:-6215MPa故最大正应力为：45MPaA1010mA(a)(b)213212FF2FqFa2FF1213a2aaFN3FFNF2FFOxOx3F2F故最大正应力为：45MPa2FA故最大正应力为：30MPa(c)A(d) 2-3如下图，对小手臂部分做受力分析，可求得：FW10F故肱二头肌中所受应力为：F1500N2.5MPaW23cmA600mm30cm30cm2-4F20100MPaa=135°时：1350cos13550MPabh11350sin213550MPacos45250MPa2450a=45°时：cos213550MPa11350450sin24550MPaa=-135°时：121350sin213550MPacos24550MPa2450a=-45°时：1450sin24550MPa各截面受力如图：2bFFh 2-5角度为a的斜截面上的正应力和切应力分别为：n210cosa0sin2a2FaF要使2粘接面21则有0cosa20sin2a20sincosaa2cosaa2sin12=arctan0.5=arcsina=arccos552-6对刚性杆AB列平衡方程：12N1N2F0:N30Ny3l3Fx0,MA()0:N12NF2AFBCNlAFBll0.476mml2l2由胡克定律：l3012EA结构中A点位移受约束，B点无约束，因此C点位移受A，B两点位移影响。而A，B点的纵向位移相同，Al1因此C点纵向位移由图知与A点纵向位移相同：Al0.476mmC 2-7建立图示坐标系，在x处横截面dd截面半径为：rxxlld截面面积为：Ax22rxttxlxl在x处横截面上所受的外力则为截面以l上所有体积的重力FxFxVxggAxdxXX0在x处横截面上所受的正应力和轴向伸长分别为xxldx2Fxgl02dxgxlAxxl2xlxxx2xgllxxdxdxxldxE2Exl000g22x2xl2lnlxl4E对该函数取一阶倒数，可知该函数没有dxgl210极值，为一个单调递增的函数，在x最dx2xl2大的地方取最大值。3gl22gl因此maxlg此处轴向变形为ll32ln20.40344EE 2-8对A点列平衡方程：NN22F1CF0:Nsin45=Nsin30N1==18.1kNx121+3ABFy0:N12cos45+Ncos30=FN=2F=25.6kN2F1+330由胡克定律：45Nl4Nl418.1kN1sin45m1111Al1=2=22=1.078mm1m0.8mEA11Ed210GPa3.1412(mm)F425.6kN0.8mNl224Nl22sin30l===1.105mm2222EA22Ed210GPa3.1415(mm)分析A点位移，A点位移后的位置为A’点。A由A点向中心线作垂线交于P点，则A点的铅直和水平位移为：APAP45AAxl30l12因为：RP+PQ=RQAQ-ARRPAll12Q所以有：Axtan30+Axtan45-Ax=0.159mmcos45cos30正号表示A’点与假设的位置相同，因此有：l2=AR+RP+tan30=1.367mmAAxcos30 2-9Fy对A点列平衡方程：Al23FFy0:kydyFk3l0l在y处截面的内力为：2fkyy213F3yNykydyky=y33l0f由胡克定律，在y截面的应变为：NyF3y3EEAEAl地桩总的缩短量为：llF3Fldyydy3EAl4EA00 2-17l对A点列平衡方程：AN2BN1Fx0:N12Ncos45NF150kNFAFy0:FN2sin45NF2250kNF45杆1的应力校核：CNN41112sAd14N1d20mms杆2的应力校核：NN2222wAn2N2b84mmw故杆1的最小直径为20mm，杆2的最小截面边宽为84mm。 2-18F由受力分析可知FFsb4FFb剪应力和挤压应力的强度条件FsF8071099.5MPa22Ad3.141.6sFFFF80kNb125MPabs2bsAd441016mmbsd钢板的2--2和3--3面为危险面1233F380kN22125MPa4(bd2)410(80216)mmFF80kN32125MPa(bd)10(8016)mmF/4123故该接头满足强度要求。 2-22F由静力平衡：F1F2F3F4F(1)Aaa(2)对2-4连线取矩：F13FeF22对1-3连线取矩：FaFa(3)24几何协调件1：由对称性，ll24又因为杆的尺寸及材料相同，由胡克定律可知FF24与方程（3）重复。a2几何协调条件2：2lll2131e3Fllii2FFF(4)物理条件：i可得：213AEA4a联立方程1-4，可解得：FeFF142aF1F2F3F4FFaaF2lFFeF41l132l22Fe3FFFaFa342a24或l12F2F1F3FF4l42l3 2-23D由静力平衡：FFF90kN(1)12A30kN/m21.8l3F1mF3m30xdxkNm(2)对A点取矩：120ABC几何协调条件:ll3211lEFl22Fl11由胡克定律:3(3)EAEA22111m2m联立方程1,2,3，可解得:FFA2F38.6kNF32.1kNF19.3kN30kN/m12A杆1受压，需校核许用压应力:F1F1c96.5MPa<1A1杆2受拉，需校核许用拉应力:F22160.5MPa>Al21l2所以杆1可安全使用，杆2有失效危险。 2-25由静力平衡：FFF(1)BC总伸长为:lllaTlCDDBCBDFFlFlCB其中lCCDlBDBCDDBEAEA1.5m1.5mFFF0B端不受约束时：CBFFF此时：lflCDaTlCBCBFlCDaTlCBEA0.571mm1.5mm2.071mm1.2mm时l所以B端受约束，此时FB0f2.1mm时lf有几何协调条件:llCDlDBaTlCB所以B端不受约束，此时FlFlCCDBDBFFCFB0由胡克定律:aTlCB(2)EAEAF200kN80MPa联立方程1,2，可解得:max2A2500mmF152.5kNF47.5kNCBF152.5kNC61MPamax2A2500mm 2-242-26钢筋：EsAsFss钢管：FA铜管：FcAccsssE200GPaE100GPasc混凝土：EcAcFccd30mmdc30mms6-1D50mma12.510Cc令长度为lls6-1a1610Clc令长度为l由静力平衡：FF(1)sc铆钉：d10mm而且钢筋受拉，混凝土受压由静力平衡：FF0(1)scFll0在拉力F下，钢筋的变形为：lEAE几何协调条件:llscsssFlFlsc拉力F卸去后，钢筋和混凝土的残余变形分别为：其中:lssaTllccaTlEAEAssccFlFlscllscFlFlEAEA则有:scaaTlTl(2)ssccscEAEAsscc其中钢筋伸长，混凝土被压缩。联立方程1,2，可解得:几何协调条件:lscllF9314NF9314NFlFllscsc0由胡克定律:(2)EAssEAccEs有两个铆钉，每个铆钉所受剪切力为:Fs联立方程1,2，可解得:2F15FFA1sccs则铆钉剪切面上的切应力为:s0c0A19AAA38scscF/2s59.3MPa2d/4 3-124232aaaa2kNm1kNm2kNm2kNm(a)(b)1130.50.5m0aaaaaa1kNm0.5kNmma01kNm2kNm(c)(d) 3-243-5dPIp外力偶矩为：M9549721Nm320n3Td/84Td1d/83127MPa实心轴的抗扭截面模量为：WpId16p1/3M16MTd/48T最大切应力为：0d045.1mmd/43255MPamaxW1Idpp3Td/216TD24d/23509MPa实心轴的抗扭截面模量为：Wp1aId16p1/3M016M0最大切应力为：maxD2446.1mmWp1adDa23.0mm223-7画扭矩图：AB段：T3-3max269.5MPaWp3MDC4Wp1aMAMB16BC段：T500Nm194MPamaxTWpmax260.0MPa300NmWpmax32.5910G 3-4对所截部分ABCDEF进行受力分析，如图可知，CDF截MM面剪力的合力为-z方向，ABE截面剪力的合力为+z方向，00BC二力大小相等，方向相反，构成的力偶方向为+y方向，ABCD截面上的力切应力所构成的合力偶为-y方向，二力偶应相互平衡。ADr设最大切应力为0，则半径r处的切应力为0EFR由切应力互等定理，则半径r处：BC计算ABCD截面切应力合力构成的力偶：rDdAM10dA2r2rLdr2rLdrArRRREF22L22rdrLR00R3L0yBC计算CDF与ABE截面切应力合力构成的力偶：xraMdAsinLsinrdrdLzD20RdArALLRR200222EFrsinddr2rdrLR0RR3000显然：MM12 3-9画扭矩图，可知实心段的最大扭矩为1.5kN.m，0.5kNm1kNm空心段的最大扭矩为1kN.m实心段中最大切应力：A6080D4D3IWp1p13216BT114.9MPamax1Wp11m1m空心段中最大切应力：3444DdDdI1Wp21p232D16DT214.6MPamax1Wp2截面B相对截A的扭转角：1NmTlTl11221.5Nm120.0092radGIGIpp12TlTl18011220.5312GIGIpp12 3-11外力偶矩为：画扭矩图，可知可能的危险截面在AC段，PM95491621Nm或是CD段1nPAC段中：d4d3M95492812NmI1W12TM1ppn3216PM954931432NmT3nmax49.4MPaWpT180M1M2M3max1.77/mGIpACDBCD段中：43d1d2d2d2TMIW3pp3216123Tmax21.3MPa0.5m0.3m1mWpT180max0.44/mGIp621Nm1432Nm 3-13P外力偶矩为：M9549390Nm0钻杆的抗扭截面模量为：n3设单位长度上土壤对钻杆的阻力D4Wp1a矩为m，则深度为y处的阻力矩为：16MMymy017.8MPamaxWp由静力平衡MlM0A，B两截面的相对扭转角为：Mm09.75Nm/m则：l则深度为y处的截面上的内力矩为：llTydymyM0dyMymyM000GIppGIMl02GIpA3M1.4810rad0B 3-15MMABMMMM0静力平衡：CABDC几何协调条件：C、D两截面的相对扭转角为零DAB即φCDφCAφABφBD05007501250MlCCA其中φCAGIpMMAMBMMCMAlABCDφABGIpMCMAMBlCAφBDGICABDp可解得：MC620NmMC380Nm620Nm由此可画出轴的扭矩图如图，可知危险截面在CA段220NmMC强度校核：maxD42.9mmWpM180刚度校核：CD65.2mmGIp380Nm因此圆轴的直径应为：D65.2mm 3-184πdI2二者的材料相同时，可看成同一材料在不同位置的切应力：p32Td/216TdTd/216Tτ11τ2max14max23IπdIπdp2p24ππd144二者的材料不同时，设杆1的扭矩为T1，杆2的扭矩为T2：Ip1Ip2d2d13232静力平衡：TTT(1)12几何协调条件：二杆之间无相对滑动，故相对扭转角相同φφ或θθ1212TT即12(2)GIGI1pp122方程1、2联立，可解得：GIGd411p11TTT1444GI2pp2GI11Gd22d1Gd1144GI22pGd22d1TTT2444GI2pp2GI11Gd22d1Gd11 4-1qFFl2313212qlABACCB231231l323ll2l2l27131FAqlFCqlFF3FFC99A22截面1截面2截面3截面1截面2截面377731剪力FSqlqlql剪力FFF0999S22弯矩M220ql220ql233ql弯矩MFlFlFl272744(a)(b) 4-12qaqa2qq123qaqa123ABBCA323112a2a2aaa33152FqaFqaFqaMqaAAA2B282截面1截面2截面3截面1截面2截面33333qa3qa剪力Fqa剪力FqaqaqaSS22222323252弯矩M1qa21qa22弯矩Mqaqaqa2qa88822(c)(d) 4-2ababFM0llFFSSFblx+xOO--Ml0FalxMal0O-x+O+MFablMMbl0(a)(b) 4-2qM0llFSFSxql2O+x-OMl0-ql2xxOO++M20Mql8M(c)(d) 4-2qFFaalFFSqlSxOO+x-FFa2ql2-O-xOxMM(e)(f) 4-2qFFa2aaaaaFSqaFSF++xOxO-qa42xqa2O-x+OFaMM(g)(h) 4-3qMM00qaaaaFFSqaSxO+xOOxOx+2+qa2MM02qaM(a)(b) 4-3qaqa2q2FFaFaaaaaFSFSxxOO--2FF29qa32Fa2qa4OxO-x-+Faqa2MM(c)(d) 4-32qqqaqqaaaaa2aFSFSqaqa+xO+xO--qaqa2xqa2O2qa-x+O2FaM2qaM252qa(e)(f) 4-32qqa210kN10kN/mqa20kNma2aa2m2m2mFFS54qaS15kNqa2+x+xO+-5kNO-10kN34qa240kNmqa220kNmqa220kNm--xOxO27qa322.5kNmMM(g)(h) 4-4注：铰支座只能提供剪力或轴力，不能提供弯矩，故铰支处弯矩为零。q2FaFq2qaBACDBACF2a2a3a2aaFSFS2F52qaFx+qa2Ox-O2F3F23qa3Fa3FaO-x-xO2qaMMFa(a)(b) 4-4qFaABCBADCD2aaaaaaFFSS32Fqa2+xxOO-F2qaFaqa22-x-xOO+MM2Faqa2(c)(d) 4-72xd2xd求出支反力FA2FFFFBllxd弯矩为：ADBCFFAy2l2xdy0yxFFllFMFAyFyxl2xdyxlxyxdlyFFFBly2xdlyxdylAFDlld故当：l20xd即x时，最大弯矩在C点2此时yxdMFF2xdlxd2x222l3dxdldCll23ld2即x时，MldFdF4Cmax28l故当x取下述两值时：xld时，最大弯矩在B点23ld当：2ldx2xFF442此时yxMB2l2xdx2x2ldxll均有最大弯矩，但作用点不同2ldldd2ldd2即x时，MFFMFF4Bmaxmax28l28l 4-852F2FS+FSkN+1512--+F2F2-12l/4l/2l/4381.5m1m1m2m2mFl830-xO18+-xMOFl8+34M46F2F12405015FF2(a)(b)6453 4-8注1：弯矩图应封闭；无集中力偶的作用，故弯矩图上不应有突变。注2：载荷图应满足静力平衡条件，即合力为零，合力偶为零。FSkN100qaF+S+-100-qa2m4m2ma2aa100kNmxOO-xqa22+qa22MM2qaq50kN/m50kN/mqq(c)(d)100kN100kN 4-10603kN求出支反力F3.36kNF7.64kNAB45画出弯矩图，可知空心部分和实心部分的危险截面空心部分：d45ABα0.75D604008002003004πD464WZ11α14.49610m320.9Mσmax162.1MPamax1W-xZ1O实心部分：+0.028πD464W21.20610mZ2321.344M(kNm)Mσmax263.4MPamax1WZ2故最大弯曲正应力为63.4MPa。 4-115kN3kN求出支反力F3.36kNF7.64kNAB6045画出弯矩图，可知空心部分和实心部分的危险截面AB空心部分：400800200300d45α0.75D604πD464WZ11α14.49610m320.9Mσmax162.1MPamax1W-xZ1O实心部分：+0.028πD464W21.20610mZ2321.344M(kNm)Mσmax263.4MPamax1WZ2故最大弯曲正应力为63.4MPa。 4-12设AB离中性轴的距离为x，CD离中性轴的距离为yσMlσMlCDCDABABlεllylεllxCDCDCDCDABABABABEEIEEIZZlx0.021ABll200mm故：ABCDly0.189CD又：xy100mm可解得：x10mmy90mm代回到伸长量的计算中：MlABM9lx0.02mm10ABEIIZZM因此，梁中的最大拉应力为：σx2030MPatIZM梁中的最大压应力为：σy30120MPaCIZ 4-13z求形心C的坐标：xC0255025分解为大矩形1和小矩形2，令小矩形2的面积为负值，则由叠加原理可知：25AyAyy1122C75xAA12C10015075507587.570.8mmy1001505075C50x因此，组合图形对Z轴的惯性矩为：132IZ1001507570.810015012132507587.570.85075126425.5910mm考虑正弯矩，使截面下方受拉，上方受压，故可能的最大拉应力为：Mσttmax70.8σM7.22kNmIZM可能的最大压应力为：σ15070.8σM25.85kNmCCmaxIZ所以该截面可承受的最大正弯矩为7.22kN.m 4-15q画出剪力及弯矩图，知：12FxSqxMxqx2所截截面为中性层，有最大切应力：Cx3FxSS3Fx3qτxxl222Abhbh梁被截下部分的切应力的合力与两侧横截面上的正应力的合力相平衡：M0右侧截面上：σ00IFzSqlMlql2左侧截面上：σlyyII2+zzx022Oql3qlFσσldAydyb24Ihh/2z2ql中性层上切应力的合力为：2l233qql-xFττxdAxdxb24bhhO0M二者合力大小相等，方向相反，相互平衡。 4-17FF求出支反力FFAB15kN画出剪力及弯矩图，知危险截面为A的左邻截面和B的右邻截面,并且两截面上剪力aaa及弯矩的绝对值大小相等：正应力校核：FFABFFMFaSmaxmaxMFaFaFσmaxσSFmax13W23Zbhb68+xb147mmO-切应力校核：F33FSmaxFaτmaxτ22bh32bhFa2b122mm-xO故截面尺寸应满足：b>=147mm,h>=221mmM 4-19F画出剪力及弯矩图，知危险截面为A的右A50邻截面：B50正应力校核：M6Fll50σmaxσmax2Wbh100ZFSFF3.75kN+x切应力校核：O3Fτmaxτ2bhxF10kNO+h胶合缝上切应力校核：y25mm=6FlFh22τyτjjM24IZF3.94kN故许可载荷为：3.75kN 4-21画出两种情况的弯矩图xOF力F直接作用时：MFl4+maxMFlFl4σmax1.3σmaxMWW4ZZxO有简支梁CD辅助作用时：+MmaxFla4Fla4MFlaσmaxσMmaxWW4ZZ故：σlmax1.3σmaxla3al1.38m13 4-2310FF画出剪力及弯矩图100求出几何量10由对称性知，形心坐标：1080100.1m2m0.1mxyCC00因此，组合图形对Z轴的惯性矩为：113364I100120801007.7310mFZS1212F正应力校核：MF0.1mmax+xMMmaxmaxOσmaxymax60mmσF206kNII-ZZ切应力校核(可参考工字形截面量的计算公式)：F2FSSz*FSbt22h02τhh0yxItZZIt824O其中：b0.1h0.2h00.1t0.02m+FSbt222F0.1m故：τmaxτy0hh0h0τF154kNItZ88M焊接面上切应力校核：y0.05mττ0.05τjjF141kN故该梁的许可载荷为141kN 5-2(a)y约束条件：qqly00y00xCC120A连续条件：234Ml2l2l92l1l1lBEIyqlqlq216242242F3B1llqllDD1239622求梁的支反力：Fql2BMBql光滑条件：2823l92l3l1lEIyqlqlq分段列微分方程并积分：2824262922311l2qlqlxqx0,/2lqllDEIyMx822221qlxl/2,ll253Dql923213148qlxqlxqxC10,/2lEIy846654Dql122qlxlD1/2,ll3842A点的挠度与转角为：9221314qlxqlxqxCxC120,/2l454253EIy16424ylqlylql128481qlxl3DxD/2,ll126 5-2(b)yFFl约束条件：xy00y00BCACC120l2l2连续条件：MB33l11lllEIyFFlDDF12B262622光滑条件：求梁的支反力：FFBMB022l11llEIyFFlD1分段列微分方程并积分：22222Fx0,/2lD10EIyMxFxl/2,llD1Fl322412FxC10,/2l2A点的挠度与转角为：EIy1Fxl2D/2,ll11ylFl3yl022413FxCxC120,/2l6EIy1Fxl3DxD/2,ll126 5-2(c)y约束条件：aby00yl0BACxC0MM00l22lDlD0212M620连续条件：lM03M03M02EIyaaCa1aaDaD12FF6ll62BCMM光滑条件：求梁的支反力：F00BFCllMM0022EIyaaC1aMaD01分段列微分方程并积分：22llM0xa0,M022lC1a22abbEIyMx6lM0xMal,M022l0D132al6lM022xC10,aaM02lD2EIy2M0x2MxDal,012lA点的挠度与转角为：M03xCxC120,aMabba()Ma()22abbEIy6lya0ya0MM3lEI3lEI00x32xDxDal,1262l 5-2(d)约束条件：yFy00C20BCAxyl0aF2allCl0CF11la66FF32lallDl12D0FBFC62求梁的支反力：FFaal光滑条件：BFFCllaFF22EIyllC11lFallD分段列微分方程并积分：22laFxl0,34laDlFEIyMxl16FxFal,llaDlalF22aF26xC10,l2lEIyFA点的挠度与转角为：x2FalxD,lla122aal()aa(32)laF3yaFyaFxCxC120,l3EI6EI6lEIyFFx32alxDxD,lla1262 5-3(a)q2将图形等效为单一载荷作用效果的叠加，得图1与图2ql33CqlqlAθθ=yθa=aC1B1C1B1B24EI24EIla图（2）又可分解为图（a）与图（b）的叠加32qlqlaθθθCaBaCb3EIEI32qlqlaθθ+=θC2CaCbq3EIEI32qlql2yθa+y=aaC2CaCbA32EIEIB故33232qlqlqla7qlqlaθθθCC12C24EI3EIEI24EIEI图(1)332322qlqlql27qalqlayyyaaa+CC12C24EI3EI2EI24EI2EI222qlqlqlACACCBB+B图(2)图(a)图(b) 5-3(a)q2用逐段刚化法将图形分解：ql（1）刚化BC段，将外载等效到B点，得图（1）ACBθC1θB1yC1θB1a图（1）又可分解为图（a）与图（b）的叠加la333qlql7qlθθ+θB1BaBb24EI3EI24EIqq22qlqlACACACBB+B图(1)图(a)图(b)2+ql（2）刚化AB段，BC段可等效为一段悬臂梁，则AB段等C效到B点的外力都可看成B点的支反力（包括剪力B和弯矩），不需单独列出，得图（2）222qlaqlaθyaC2C2EI2EI32图(2)故7qlqlaθθθCC12C24EIEI3227qlaqlayyyθayCC1C2C1C224EI2EI 5-3(b)FFl将图形等效为单一载荷作用效果的叠加，得图1与图2ACBθθθAA12Aθθθl/2l/2BB12ByyyCC12CFl其中：333FlFlFlθθyA1B1C1ACB3EI6EI16EI333FlFlFlθθyl/2l/2A216EIB216EIC248EI图(1)故有+319FlθθθFAA12A48EI311FlACBθθθBB12B48EI3Fll/2l/2yCyC12yC12EI图(2) 5-4yF要使滚轮恰好走一水平路径，则梁预先弯曲的程度必须与滚轮走到该处时梁的挠度相同。x（a）滚轮走到x处时，x处梁的挠度为：3xFxyxl3EI3Fx则梁应预先弯曲为曲线：3EI(a)Fyx（b）滚轮走到x处时，x处梁的挠度为：AB22Fxlxyxx3lEI22Fxlxl则梁应预先弯曲为曲线：3lEI(b) 5-5q画出剪力与弯矩图，知最大弯矩为：2qlMmax8l正应力强度校核：22Mql/84qlσmaxσFmax33SWπdπdZ32+xOd155mm-ql2刚度校核：44x55qlqllymax4σO384EI6Eπd200+Zd280mm2Mql8故梁截面的最小直径为280mm 5-6l1/2l1600mml500mml1000mm23l/221CB计算支反力：FACFFFFD3FCDF用逐段刚化法将图形分解：Al2（1）刚化DH段，将外载等效到D点，得图（1），F其中力F平衡到D点后可计入D点支反力，因Al3H此不用单独列出，即此时FFD2FD（2）刚化ACD段，DH段可等效为一段悬臂梁，则ACD段等效到D点的外力都可看成D点的支反力（包括剪力和弯矩），不需单独列出，得图（2）3Flyyyy3CHH12HH23EIBFl3DFD+Al3HH图(1)图(2) 5-6CCBFlB3Fl3BFDDAHA2F+HF图(1)图(a)图(b)图（1）又可分解为图（a）与图（b）的叠加,H点的挠度包括由AB梁的变形，B点位移引起的H点的牵连变形，如图（c）；和在弯矩Fl3作用下，简支梁BD变形C引起的H点的牵连位移。lyy+=y3yθlH13HaHbBDblBD2A32Fl1Fll322l348EI3EIH323故有：Fl3Fl1Fll23yyyHH12H3EI12EI3EI图(c)6.5042.8103.252mm12.566mm 6-3F短木柱中任意点的应力状态为30FAx0yxy0沿木纹方向的剪应力为xy360sin120xycos12024或画出应力圆，半径为：R2603Rsin60120604603F1MPa4A法向为x正向的平面F23.1kN 6-7面a和面b中的应力分别为：a2p602p603p3p602p603p30代入公式中：30xyxycos120sin1202p60xy3p225pxxysin120cos1203pp60xyy2p2b0xyxy60sin120xycos1203p2pa即，x,y正向即为主应力方向。5p3p120或画出应力圆，将a,b两点标在圆中，又两平面法2p向关系为，a顺时间旋转120°到b平面，即在应力圆中的矢径为：a顺时间旋转240°到b点。则应力3p圆的半径为：Rp2b圆心为（3p,0）a顺时间旋转120°到b主应力点，即实际空间中，面a顺时间旋转120°到主应力平面 6-8面AB和应力为零，故为一主应力平面Aa090axy15MPaxyaa15MPa面AB距x正向，即AC面为135°，故有45BCxyxy135cos270xysin27002215MPaa15MPaxysin270cos2700135xy2或画出应力圆，AB与AC两平面垂直，故在应力圆中为一条直径的两个端点。又由切应力互等定理，BC有a即两点横坐标相等，纵坐标绝对值相等，故为一条垂直于横轴的直径，如图AB15AB面对应坐标圆点，三点可确定应力圆R15MPa圆心为（15,0）30MPaAC主应力单元体为：45 6-16yxxy13xxy0.41080MPaEx100.12103yyyxE 6-17解法一：0xyCxyll有ACAC302530xyxy33因为30cos60xysin60A2242xyxy360cos120xysin1202242由广义虎克定律1303060E故3l9.2810mmAC或者画应力圆，在圆中找出30°和60°方向的正应力值15如图R2302453060Rcos15306021560Rcos152 6-17解法二：xy0xyC由广义虎克定律2511xy30xxyyyxxyEEGAE其中G21故xyxyxy30cos60sin6022223ll9.2810mmACAC3030或者画应变圆，在圆中找出30°方向的正应变值60如图R2602Rcos15302Rcos15602 6-18y0x120xyxyxycos240sin240120222xyxyxyxcos480sin480240120O222120x0220120240y32xy1202403xy122max/minxyxy22故012024022220120120240240033xy3240120tan2a02xy0120240 6-19F2F求出支反力FFAFB1m2m3345No28a中性层上的点为纯剪切应力状态对应的主应力状态为FAFB1203113故0.260104531EE***FSFS2FSszAzz其中IbIb3IbzzzIz对28a号工字钢，查表可知246mmb8.5mm*Sz故F133.8kN 6-20dF500500对18a号工字刚，查表可知其尺寸b和几何性质9045hyAh440I166010mmz34.3tNo18ah180mmt10.7mm250b6.5mmd94mmFAhF故y45mmB4载荷变化15kN时，A点截面处的剪力A点处43和变矩的变化量分别为S34.36.562.1510.79484.659.9010mmzFF7.5kNSA2故由广义虎克定律MF0.25m1.875kNmxMyA6A0x24.2102EEIzx66.81090y0A点应力状态为AExyxyxycos90sin9045xy0xy222MFS1111FSSAz6AySAzxxy050.610其中22EEEIbzIIbzz 7-2yF2画出弯矩图显然，危险截面为固支端截面xh固支端截面的四个角点为危险点F设在F1作用下产生的应力为F1z1b在F2作用下产生的应力为1m1mF2则固支端截面的四个角点的应力状态分别为ABMF1F2F1F2yABF2m1CDF1F2F1F2CDF1m2Mz故B，C两点为危险点MM1max2max2FF12136FFmaxFF1max2max22312WyzWhb6bh6b2max10MPa故b89.9mm 7-4FBy由几何关系可知：B2msinα0.8cosα0.62.5m2.5m1m由静力平衡：CFFsinα2.4kNAxFa1mFx0:FAxFsinα0Ay1FFcosα0.9kNaFFy0:FAyFByFcosαAy2Al1MA0:FBylFcosαFFBycosα0.9kNF22Ax画出剪力图和弯矩图，知C的左邻截面有最大压应力，C的右邻截面有最大拉应力FNmax2.4kNMmaxFAyl21.125kNm-2.4kN正方形截面：Waz1130.1m3366最大拉应力：Mσmax6.75MPatmaxW+z最大压应力：MF1.125kNmσmaxNmax6.99MPacmax2Waz 7-7y横截面上形心坐标为z1z22050906020502010010IIF12kNz22020506020201005010040.48mm200F206020故zz1210059.52mm2横截面积A5020206020104200mm3335020220602100202Iy5020z110206050z220100z210121212644.8810mmI-I截面受轴力与弯矩FN12kNMF0.2z22.89kNm故MFNz26.8MPatmax2IAyMFzN32.3MPacmax1IAy 7-9zz400300300300DACBxRyO2R1PPF考察钢轴DB的强度，因此将外载P等效到支由静力平衡：点C，将力F等效到O处，可画出OB的受力图，如图(不知道OD的长度，因此设OD段也是钢Mx0:0.15P0.5FFP0.3轴，对OB轴做整体考虑)zFFz0:FAzFBzPFBzM2AzMM0:FACFCBDA1CBxCyAzAzOFFAzFBz0.5PFBFAFFFF0:FAFFBFFPMCz0:FAFACFBFCBFOC其中：MPR0.15NmP12FP0.5AFMFR0.5NmF21FP0.2BF 7-9显然，此时有最大弯曲正应力。因此，轴OB受到绕x轴的扭转，和xz，xF平所以危险截面为C的左邻截面，截面内的弯曲，画出轴的扭矩、弯矩图：面的危险点为轴的外边缘点，受力状态如图：0.15PT+xx+弯扭组合变形时，第四强度理论MF0.06P的等效应力为：0.12P22MT0.75xσr4WzMy+220.21PP0.75(0.15)=σ=80MPa3πd0.15P32因为摇臂在转动中，力F保持垂直于摇臂，因此当摇臂摇到力F与P的方向一致时，有最P859N大弯矩，此时只有xz平面内弯曲，弯矩图为：xMy+0.21P 7-10电动机转子两个轮子自重砂轮dTQ1101NQ2275NQD2Q2Q转子传递的扭矩为1FzABFPFyT955020.46Nmy130240180n由平衡关系，支座A，B的支反力DMxzFT0经过轴线，不能提供扭矩2FFByAyFFBzAzFz故Fz163.68NFFyz3491.04NQQF12y由Fy0FAy408.81NM0F293.77NzByFz0FAz252.34NM0F88.66NyBz 7-10电动机转子砂轮dTQD2Q2Q1FzABFFyy130240180画出内力图，可知危险截面为支座A处20.46Nm因为截面为圆形，所以最大应力一定在截面边缘处取到。此处可取合弯矩进行计算，故截面A处T22MMMtotalzy18.18Nm3Mdz圆形截面Wz3228.08Nm按第三强度理论2222221.28NmMTtotalMzyMT3.3MPaMr3yWWzz故此轴安全。 7-12F32FF22画出轴的受力图12B3由静力平衡，求各处支反力A由Mx0B2F33F2F11dddF12FF3200400200200123222F2kN3FAyFd13F2由1FBy23F3Fy0FAy2.25kNdF2dF2F3M0F225kNAz2FBz3zBy23F1Fz0FAz1.5kNM0F7.5kNyBz 7-12F32FF22画出内力图，可知危险截面在轮2的右12B3侧截面，或是支座B处3AdB2F圆形截面W33zF2F1321200400200200由第三强度理论对轮2的右侧截面0.45kNm22222MTMMTtotalBzByB0.225kNmr3WWTzz2224504509000.45kNmWzMz对支座B处0.45kNmMT2222ByB4501200r3WWzzMy60.5MPa<80MPa故危险截面为支座B处，此轴安全。1.2kNm 7-17F画出内力图yaCD点位于中性轴上，对应的主应D为纯剪切应力状态力状态为AxzB此时的切应力包括有扭转切应力和弯曲切应力FTl2l2扭转最大切应力1Wp45Fax4FAD弯曲最大切应力，对圆形截面杆s2B3AD点位于外表面，z轴正向，此处弯曲T4FsD12剪应力向下，扭转剪应力向上，故WA3FapT111Fa4F45113DEEEW3ApFlF3.484kN此时的危险截面为截面A，由第三强度理论Mz22MTAAr3142MPa<1.05Wz故此曲拐安全。 7-211005Fy1200200ACBzy22m1m1010转换后的截面的对z轴的惯性矩为选钢（材料2）为基本材料，将上部的1001032木材等效为钢材。模量比Iz1001057.5512E3nw0.0552002200511057.5Es12转换后的截面为T字形，原木梁部分宽8.85410mm64度为100n5mmM2F截面C处有最大弯矩，为3转换后的截面的形心坐标为M2005110101005木梁中有最大压应力cmaxny15.74MPaIyz2200510100M钢梁中有最大拉应力y43.3MPa57.5mmtmax2Iz故y1152.5mm查表得截面C挠度F214y2.51mmc18EIz'