【人教版】数学必修三《几何概型》课后练习(含答案).doc 10页

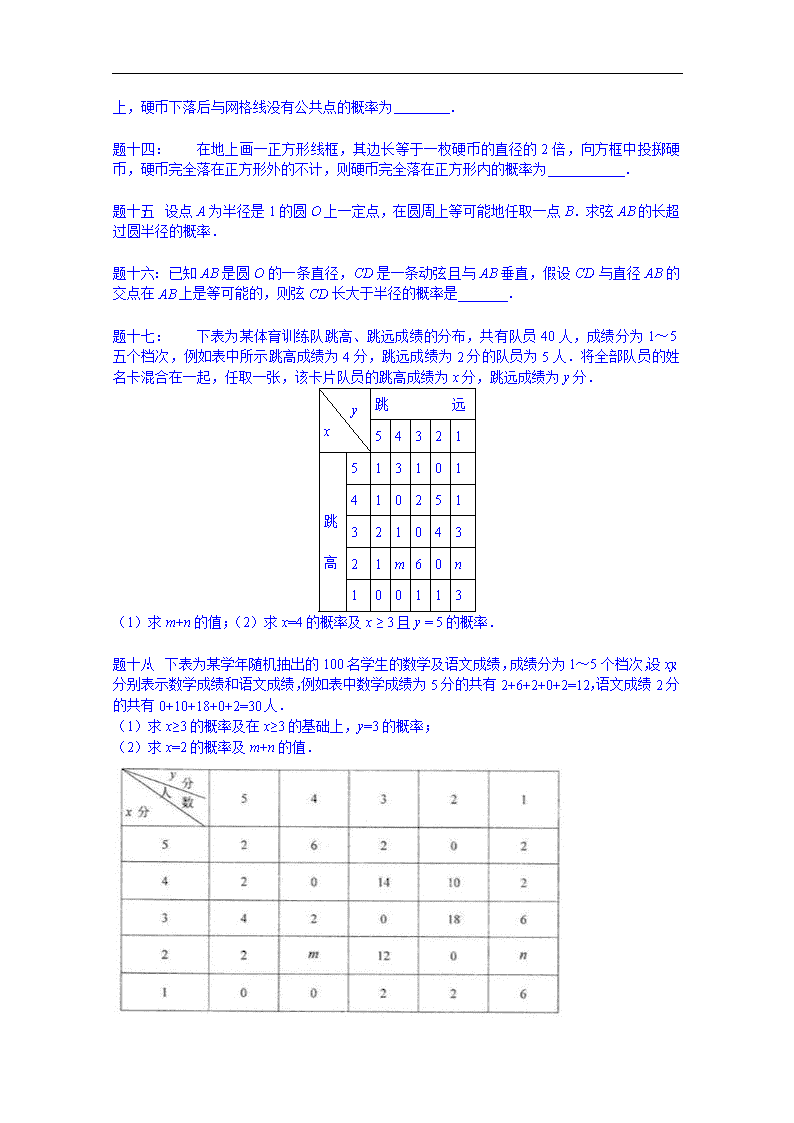
'www.ks5u.com几何概型课后练习主讲教师：熊丹北京五中数学教师题一：射箭比赛的箭靶涂有五个彩色得分环.从外向内为白色，黑色，蓝色，红色，靶心是金色，金色靶心叫“黄心”．奥运会的比赛靶面直径为122cm，靶心直径为12.2cm．运动员在70m外射箭.假设射箭都能射中靶面内任何一点都是等可能的．问射中黄心的概率为多少？题二：如图，矩形ABCD中，点E为边CD的中点，若在矩形ABCD内部随机取一个点Q，则点Q取自△ABE内部的概率等于(　　)A．B．C．D．题三：在体积为V的三棱锥S-ABC的棱AB上任取一点P，则三棱锥P-SBC的体积大于的概率是．题四：一个三棱锥的三视图是三个直角三角形，如图所示，在包围该三棱锥的外接球内任取一点，该点落在三棱锥内部的概率为． 题一：已知P是△ABC所在平面内一点，＋＋2＝0，现将一粒黄豆随机撒在△PBC内，则黄豆落在△PBC内的概率是(　　)A．B．C．D．题二：在区间(0,1)内任取两个实数，则这两个实数的和大于的概率为(　　)A．B．C．D．题三：若m∈(0,3)，则直线(m＋2)x＋(3－m)y－3＝0与x轴、y轴围成的三角形的面积小于的概率为________．题四：平面上画了一些彼此相距2a的平行线，把一枚半径r的部分如图中阴影部分所示．所以这两个实数的和大于的概率为1－××＝．题四：． 详解：直线与两个坐标轴的交点分别为(，0)，(0，)，又当m∈(0,3)时，>0，>0，∴··<，解得0r时，硬币与直线不相碰．∴P＝＝．题二：π．详解：以A、B、C为圆心，以1为半径作圆，与△ABC交出三个扇形，当P落在其内时，符合要求．∴P＝＝．题三：．详解：如图，△AOB为区域M，扇形COD为区域M内的区域N，A(3,3)，B(1，－1)，S△AOB＝××3＝3，S扇形COD＝，所以豆子落在区域N内的概率为P＝＝．题四：A．详解：面积为36cm2时，边长AM＝6cm；面积为81cm2时，边长AM＝9cm．∴P＝＝＝．题五：C．详解：如图，在AB边上取点P′，使＝，则P只能在AP′上(不包括P′点)运动，则所求概率为＝． 题一：．详解：因为硬币的直径是1，所以半径是，要使硬币下落后与网格线没有公共点，只需硬币下落在正中心的边长为3的正方形的内部∴所求概率为．题二：．详解：设硬币的直径为2cm，正方形线框的边长为4．考虑圆心的运动情况．因为每次投掷都落在最大的正方形内或与最大的正方形有公共点，所以圆心的最大限度为原正方形向外再扩张1个小圆半径的区域，且四角为四分之圆弧；此时总面积为：4×4+4×4×1+π×12=32+π；完全落在最大的正方形内时，圆心的位置在2为边长的正方形内，其面积为：2×2=4；∴硬币落下后完全在最大的正方形内的概率为：．题三：．详解：在圆上其他位置任取一点B，圆半径为1，则B点位置所有情况对应的弧长为圆的周长2π，其中满足条件AB的长度大于等于半径长度的对应的弧长为，则AB弦的长度大于等于半径长度的概率． 题一：．详解：设弦CD长大于半径的概率是P，如图所示：E，F两点为CD长恰为半径时的位置，根据几何概型长度类型，可得：．题二：（1）m+n的值为3；（2）x=4的概率为，x≥3且y=5的概率为．详解：（1）表中反映了队员的跳高、跳远的综合成绩，其中各单元格的数字之和等于40即：1+3+1+0+1+1+0+2+5+1+2+1+0+4+3+1+m+6+0+n+0+0+1+1+3=40．整理，得m+n+37=40，因此m+n=3．（2）∵x=4的人数为1+0+2+5+1=9，∴x=4的概率为：．又∵x≥3且y=5的人数为1+1+2=4，∴x≥3且y=5的概率为．答：（1）m+n的值为3；（2）x=4的概率为，x≥3且y=5的概率为．题三：（1），；（2）．详解：（1）当x=3时，共有4+2+0+18+6=30人；当x=4时，共有2+0+14+10+2=28人；当x=5时，共有12人，故当x≥3时：概率，在x≥3的基础上，y=3时有 2+14+0=16人，故此时概率为．（2）当x=1时，共有0+0+2+2+6=10人，故当x=2时，共有100-（10+70）=20人，此时概率为，∴2+m+12+0+n=20，∴m+n=6．'