jmp在半导体行业的应用(1)_企业管理_质量管理_822 12页

'JMP在半导体行业的应用(1)_企业管理_质量管理   实验概要   问题的由来   由于工艺的精度要求，实验设计在半导体工业中应用越来越广。因为半导体生产设备正变得越来越复杂，多个工艺因子必须在同一描述中被研究。因为有多个工艺因子，首先要考虑的往往是筛选实验。筛选实验对于筛选主要因子及甄别交互作用效率是最高的。因为筛选实验研究多因子而实验处理序列较少，但是，它们的结果会导致混杂。所以它经常不能辨别因子的交互作用，而要解决之，往往是增加实验处理序列。   一个案例是气相刻蚀设备在150mm硅片转移加工200mm硅片中通过增加少量实验处理来解决混杂的问题。为了精确描述新刻蚀工艺的气相刻蚀设备，实施了一个6因子16个处理，加上2个中心点的实验处理，分辨率为IV的筛选实验（共18个处理）。实验分析了6个因子9个交互作用的混杂情况来达到改善均匀性的目的。要分清哪些交互作用只有这16个处理是根本不可能的。通常的方法是根据折叠原则增加16个处理，这些处理是增加另一个6因子完全析因实验26的1/4部分析因设计。但这种通常的方法将要34个实验处理，几乎扩大了一倍的实验处理，这些对于时间与资源都是不允许的，所以提出了一个现实的问题：是否可能用更少的实验处理来解决此类混杂问题。   解决策略   学术论文上曾发表过仅用8个实验次数来代替增加的16个处理的文章，即用26个处理来代替34个处理。这增加的8个处理与原来的16个处理一起组成3/4部分析因实验，由于增加的8个处理，9个交互作用中的7个将被估算出来。   结论   新增8个实验处理后，生成了适合26个处理的模型，这个模型用于工艺设置的预估与优化。这些预估被实验来检验。结果显示当氧化层刻蚀厚度为200Å时与模型预估吻合，当氧化层刻蚀厚度为50Å时，实际观察到的厚度比模型中预估的要大。但是，通过这些预估，工程师改变了一个因子的设置，通过这次改进，氧化层刻蚀厚度为50Å时的均匀性也满足了要求。   从这个刻蚀均匀性实验可以得出，筛选实验的混杂问题不一定要通过成倍折叠来解决。通过半折叠形成一个3/4部分析因设计，增加折叠处理数的一半来找到解决交互作用的混杂问题的合适模型。减少实验次数并不是总是可能的，但是在折叠设计前总先考虑一下半折叠设计。对很多工艺来说，这些减少导致时间的节省与资源的节约。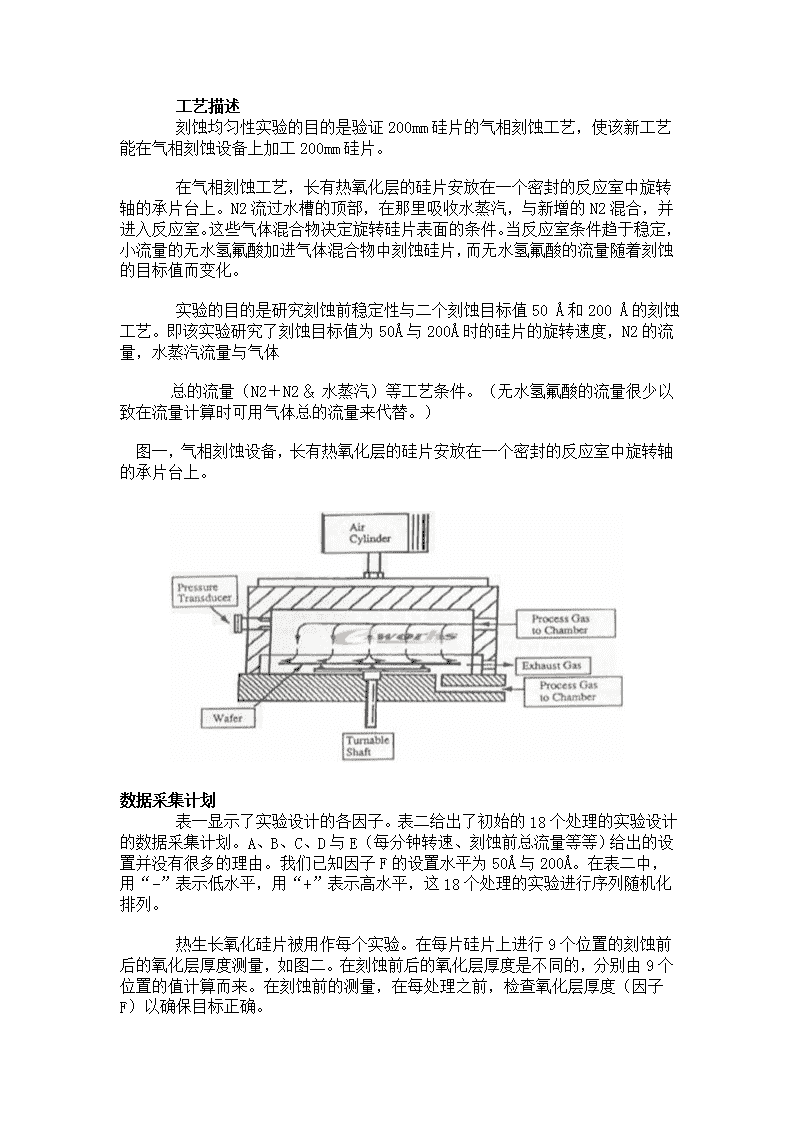    工艺描述   刻蚀均匀性实验的目的是验证200mm硅片的气相刻蚀工艺，使该新工艺能在气相刻蚀设备上加工200mm硅片。   在气相刻蚀工艺，长有热氧化层的硅片安放在一个密封的反应室中旋转轴的承片台上。N2流过水槽的顶部，在那里吸收水蒸汽，与新增的N2混合，并进入反应室。这些气体混合物决定旋转硅片表面的条件。当反应室条件趋于稳定，小流量的无水氢氟酸加进气体混合物中刻蚀硅片，而无水氢氟酸的流量随着刻蚀的目标值而变化。   实验的目的是研究刻蚀前稳定性与二个刻蚀目标值50Å和200Å的刻蚀工艺。即该实验研究了刻蚀目标值为50Å与200Å时的硅片的旋转速度，N2的流量，水蒸汽流量与气体   总的流量（N2＋N2＆水蒸汽）等工艺条件。（无水氢氟酸的流量很少以致在流量计算时可用气体总的流量来代替。）　图一，气相刻蚀设备，长有热氧化层的硅片安放在一个密封的反应室中旋转轴的承片台上。数据采集计划   表一显示了实验设计的各因子。表二给出了初始的18个处理的实验设计的数据采集计划。A、B、C、D与E（每分钟转速、刻蚀前总流量等等）给出的设置并没有很多的理由。我们已知因子F的设置水平为50Å与200Å。在表二中，用“-”表示低水平，用“+”表示高水平，这18个处理的实验进行序列随机化排列。   热生长氧化硅片被用作每个实验。在每片硅片上进行9个位置的刻蚀前后的氧化层厚度测量，如图二。在刻蚀前后的氧化层厚度是不同的，分别由9个位置的值计算而来。在刻蚀前的测量，在每处理之前，检查氧化层厚度（因子F）以确保目标正确。    表一，刻蚀均匀性实验的6个因子                  指标描述如下：   每片硅片上9点的氧化层厚度的标准偏差（S.D.）；   每片硅片上9点的氧化层厚度的刻蚀均匀性。这里的均匀性用标准偏差除以平均值的百分数；   刻蚀均匀性的自然对数。   工程技术人员往往使用均匀性，而统计学家往往更喜欢使用标准偏差。均匀性的自然对数主要用于改进统计分析，因为该实验的均匀性值有较大的范围（最大的值几乎是最小值的90倍。）三个相关的指标观察是否能得出相同的结论？氧化层的平均值不考虑作为一个指标，因为它能被刻蚀的时间严格来控制。   表二，初始18个处理的实验数据采集计划          表二中的开始16个处理生成了1/4部分析因实验，完全析因实验应为64个处理。第17,18个处理是中心点，用于预估实验误差，它们对于判别主效果与交互作用是无贡献的，所以我们暂不考虑它们的影响。    图二，显示每片硅片上用于计算的9个位置的分布。       从初始16个处理的生成器可知，E=ABC与F=BCD，定义关系为：I=ABCE=BCDF=ADEF。通过这些别名关系定义，可以确定二交互项的别名关系，见表三。在计算这些别名关系时，我们假设有三个或更多的交互作用是可以被忽略的，注意每个2因子交互作用至少与其它一对交互作用产生混杂。   表三上有三个星号（*），对取自然对数的指标而言表示别名是重要的，对标准偏差也是重要的。混杂意谓着，给出AC+BE是重要的，它不能告诉你，是AC重要还是BE重要，还是二者都重要。同样的道理，其它三组的混杂问题相似。为了解决这个混杂问题，增加了8个新的设置处理。这些8个设置是通过表二中A因子是低因水平（－）时保留其它因子的设置，但A因子的水平设置为高水平（＋），见表四。注意，其它因子的水平没有变化，这种设置称为对于因子A的半折叠实验设计。总的实验次数为16＋8＝24处理（省略2个中心处理）的3/4部分析因实验，因为24个处理是32个处理的3/4，所以称为3/4部分析因实验。   半折叠设计，能够从24个处理中预估涉及到A与E的交互作用项，那样，表三中的9个交互作用就可以预估了。预估能力指19项有合适的模型给出，1个常数项，6个主效果项（A、B、C、D、E、F），与12项交互项（AB，CE，AC，BE，AD，EF，AE，[BC或DF]，AF，DE，[BD或CF]，与[BF或CD]）。A因子的半折叠设计不解决生成器BCDF的问题。在初始的16个处理的实验中，9个交互项是潜在的重要项。增加了8个半折叠，其中的7个交互项能够预估。因为工程师根据知识知道，交互作用DF是可以忽略的，因而通过BC＋DF的别名关系，BC的重要性就能确定。   表三显示了初始16个处理的取自然对数的均匀性指标的回归结果。利用最小二乘法回归模型预估各项系数与标准误，t-ratio,与P值。这3个带“＊”号的项表示是重要的别名关系。               数据分析与结果解释   我们从表二与表四中的26个处理中来分析氧化层厚度的标准偏差（S.D.），刻蚀均匀性与刻蚀均匀性的自然对数指标。   从表二可以看出，氧化层厚度均匀性范围从0.80到71.00之间，这是非常大的极差。（71.00几乎是0.80的90倍），所以建议用自然对数或平方根转换。通过自然对数转换后范围从-0.22到4.26，明显缩小。自然对数转换能够获得更好的模型，能更精确地确定主效果与交互作用的显著性评判。   第15个处理的氧化层厚度均匀性值为71.00，如果不进行转换，往往作为奇异的点而被过滤掉，但是通过自然对数的转换后，该点也参与回归运算，能够达到更好的R2，所以我们用自然对数转换会更好，尽管二者推荐的优化设置是一样的，正是这些理由，转换后的指标作为本论文的指标作为测量氧化层厚度变异的指标。   表四，增加8个处理的对因子A的半折叠设计实验数据采集计划。   因为最后增加的8个处理，是在前面18个处理后几周实施的，所有我们增加了区组的考虑，前面18个处理为低水平（－1），而后8个处理为高水平（1），如下所示：    我们用逐步回归法进行回归分析，表五是这些算法的结果，可以从右图中可以看到，随着逐步回归法的进行，R2逐渐增大，把Prob>F列的值＜0.05的值全部选择后，R2值为0.9186,如果增加AE与AD，则R2从0.9186到0.9507,变化比较小，所以AE与AD的交互作用可以忽略。模型可参见表六与表七。   表五是这些算法的结果，由于从右图可知，如果增加AE与AD，则R2从0.9186到0.9507,变化比较小，所以AE与AD的交互作用可以忽略。　图三为B＝－1，E＝1时F因子刻蚀量（50Å或200Å）与 A因子每分钟转速的等高图。这个图显示，当低水平的F因子时，A因子也取低水平；当高水平的F因子时，A因子也取高水平。        表六显示了对于氧化层厚度取自然对数的均匀性重要性显著的因子只有E与F，表七显示了模型的适合性指标。表八给出了只有显著性效果的减少模型，表中只有主效果E与F，与交互作用AF，BC与EF，还有区组因子。表九显示了模型的总概信息，在最后的模型中，只保　留了主效果E与F，R2的值由原来的0.918减少到0.906,（可以忽略的限度）。表征这个模型的方程为：      刻蚀均匀性为   ＝exp[1.95-0.464E -0.532F+0.20Block+0.285EF -0.434BC -0.375AF]      表六，显示了对于氧化层厚度取自然对数的均匀性重要性显著的因子，包括所有主效果与交互作用AF，BC与EF，还有区组因子。给出了预估系数，标准误，t-ratio与显著性评判Prob>|t|.      表七显示了模型的适合性指标。    图四为A＝1，E＝1与F＝1时，B因子（刻蚀前总流量，N2+N2和水蒸汽）与C因子（刻蚀前气流量）的等高图。从图可知，低水平的B因子与低水平的C因子是好的操作条件，与已知的高水平的B因子与高水平的C因子几乎一样好。            表八给出了只有显著性效果的减少模型，表中只有主效果E与F，与交互作用AF，BC与EF，还有区组因子。  表九显示了模型的总概信息，在最后的模型中，只保留了主效果E与F，R2的值由原来的0.918减少到0.906,（可以忽略的限度）。     图五，当B＝1，C＝1，A＝1时，E因子（刻蚀气流量）与F因子（刻蚀量，50Å或200Å）的等高图。从图上可知，不管F因子取高还是低的水平，E因子总是取高的水平。          验证实验   表十给出了F因子（刻蚀量，50Å 或200Å）是低水平与高水平的最佳设计，因子B与C使用新的条件设置。一个确认实验被安排实施。表十也比较了这些设置的结果，验证结果证实，F因子取200Å时，预估是正确的，因为实际观察值正好落在置信区间内。当F因子取50Å时，实际观察值比模型预估的值要大，然而，工程师改变了因子A，使它接近中心点值，这样，50?时的均匀值减少到3.7%,满足了均匀性要求，当然也希望增加E因子（刻蚀气流量）的值，但是受到流量的限制，实际上是不可能的。   结论与推荐方案   本实验是一个通过仔细推敲数据而设计的一个增强的筛选实验，仅仅增加了8个处理的实验处理序列就几乎解决了感兴趣的交互作用。根据标准做法，16个处理是要求增加的。但是，我们通过半折叠的实验设计，节省时间与节约了资源，并超越了实验的目标。   图六为三组交互作用图，AF，BC与EF。       表十，为推荐的各水平设置。               [参考文献]      1,AppliedStatisticsandprobabilityforengineers;DouglasC.MontgomeryGeorgeC.Runger   2,DesignandanalysisofExperiments;DouglasC.Montgomery   Theabove2booksarepublishedbyJohnWiley&Sons,Inc.   3,改进工艺，优化核心流程教材第五册，第六册，闵亚能　2005   4,StatisticsforExperimenters.Wiley,NewYork.GeorgeE.P.Box,WilliamG.Hunter,andJ.StuartHunter(1978).   5,StatisticalDesignandAnalysisofExperiments;Wiley,NewYork.RobertL.Mason,RichardF.Gunst,andJamesL.Hess(1989).   6,DesignandAnalysisofExperiments,4thedition.Wiley,NewYork.DouglasC.Montgomery(1997).   7,JMPStatisticsandGraphicsGuide,SASinstitute,Cary,NorthCarolina.   8,JMPmanual:DesignofExperimentGuide&StatisticsandGraphicsGuide   9,MotorolaUniversity:Leadership,Learning&Performanceserialbooks.    实验概要   问题的由来   由于工艺的精度要求，实验设计在半导体工业中应用越来越广。因为半导体生产设备正变得越来越复杂，多个工艺因子必须在同一描述中被研究。因为有多个工艺因子，首先要考虑的往往是筛选实验。筛选实验对于筛选主要因子及甄别交互作用效率是最高的。因为筛选实验研究多因子而实验处理序列较少，但是，它们的结果会导致混杂。所以它经常不能辨别因子的交互作用，而要解决之，往往是增加实验处理序列。   一个案例是气相刻蚀设备在150mm硅片转移加工200mm硅片中通过增加少量实验处理来解决混杂的问题。为了精确描述新刻蚀工艺的气相刻蚀设备，实施了一个6因子16个处理，加上2个中心点的实验处理，分辨率为IV的筛选实验（共18个处理）。实验分析了6个因子9个交互作用的混杂情况来达到改善均匀性的目的。要分清哪些交互作用只有这16个处理是根本不可能的。通常的方法是根据折叠原则增加16个处理，这些处理是增加另一个6因子完全析因实验26的1/4部分析因设计。但这种通常的方法将要34个实验处理，几乎扩大了一倍的实验处理，这些对于时间与资源都是不允许的，所以提出了一个现实的问题：是否可能用更少的实验处理来解决此类混杂问题。   解决策略   学术论文上曾发表过仅用8个实验次数来代替增加的16个处理的文章，即用26个处理来代替34个处理。这增加的8个处理与原来的16个处理一起组成3/4部分析因实验，由于增加的8个处理，9个交互作用中的7个将被估算出来。   结论   新增8个实验处理后，生成了适合26个处理的模型，这个模型用于工艺设置的预估与优化。这些预估被实验来检验。结果显示当氧化层刻蚀厚度为200Å时与模型预估吻合，当氧化层刻蚀厚度为50Å时，实际观察到的厚度比模型中预估的要大。但是，通过这些预估，工程师改变了一个因子的设置，通过这次改进，氧化层刻蚀厚度为50Å时的均匀性也满足了要求。   从这个刻蚀均匀性实验可以得出，筛选实验的混杂问题不一定要通过成倍折叠来解决。通过半折叠形成一个3/4部分析因设计，增加折叠处理数的一半来找到解决交互作用的混杂问题的合适模型。减少实验次数并不是总是可能的，但是在折叠设计前总先考虑一下半折叠设计。对很多工艺来说，这些减少导致时间的节省与资源的节约。   工艺描述   刻蚀均匀性实验的目的是验证200mm硅片的气相刻蚀工艺，使该新工艺能在气相刻蚀设备上加工200mm硅片。    在气相刻蚀工艺，长有热氧化层的硅片安放在一个密封的反应室中旋转轴的承片台上。N2流过水槽的顶部，在那里吸收水蒸汽，与新增的N2混合，并进入反应室。这些气体混合物决定旋转硅片表面的条件。当反应室条件趋于稳定，小流量的无水氢氟酸加进气体混合物中刻蚀硅片，而无水氢氟酸的流量随着刻蚀的目标值而变化。   实验的目的是研究刻蚀前稳定性与二个刻蚀目标值50Å和200Å的刻蚀工艺。即该实验研究了刻蚀目标值为50Å与200Å时的硅片的旋转速度，N2的流量，水蒸汽流量与气体   总的流量（N2＋N2＆水蒸汽）等工艺条件。（无水氢氟酸的流量很少以致在流量计算时可用气体总的流量来代替。）　图一，气相刻蚀设备，长有热氧化层的硅片安放在一个密封的反应室中旋转轴的承片台上。'